等差数列
图片预览











文档简介
(共115张PPT)
鸡蛋,从外打破是食物,从内打破是生命。人生亦是,从外打破是压力,从内打破是成长。如果你等待别人从外打破你,那么你注定成为别人的食物;如果能让自己从内打破,那么你会发现自己的成长相当于一种重生。
2.2 等差数列
第一课时
一、数列的定义,通项公式:
按一定次序排成的一列数叫做数列。一般写成a1,a2,a3 ,… an,…
如果数列{an}的第n项an与n的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式。
二、数列的简单表示:
三、给出数列的方法:
www.
复习
在过去的三百多年里,人们分别在下列时间里观测到了哈雷慧星:
(1)1682,1758,1834,1910,1986,( )
你能预测出下一次的大致时间吗?
2062
相差76
某此系统抽样所抽取的样本号分别是:
7,19,31,43,55,67,79,91,103,115.
某长跑运动员7天里每天的训练量(单位:m)是:
7500,8000,8500,9000,10000,10500.
(观察以下数列)
引入
这三个数列有何共同特征
从第2项起,每一项与其前一项之差等于同一个常数。
请尝试着给具有上述特征的特殊数列
用数学的语言下定义
交流
1、等差数列的定义
如果一个数列从第2项起,每一项与其前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母d表示。
(1)指出定义中的关键词:
从第2项起
等于同一个常数
⑵由定义得等差数列的递推公式:
说明:此公式是判断、证明一个数列是否为等差数列的主要依据.
每一项与其前一项的差
探究
练习:判断下列数列中哪些是等差数列,哪些不是?如果是,写出首项a1和公差d, 如果不是,说明理由。
www.
(6)
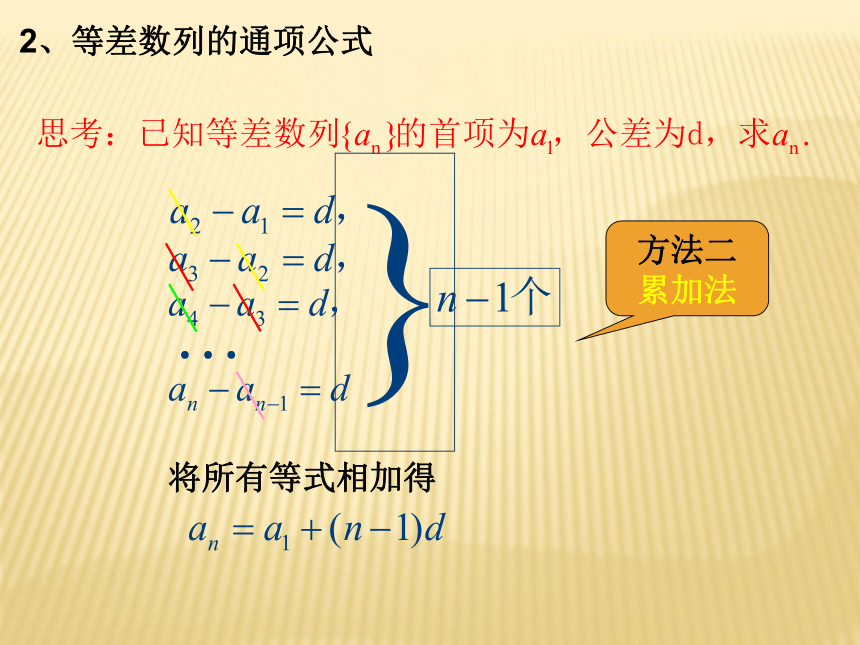
2、等差数列的通项公式
根据等差数列的定义得到
方法一:不完全归纳法
2、等差数列的通项公式
将所有等式相加得
方法二
累加法
例1 ⑴求等差数列8,5,2,…的第20项.
⑵- 401是不是等差数列-5,-9,-13,…的项?如果是,是第几项?
解:
⑴由a1=8,d=5-8=-3,n=20,得
a20=8+(20-1) ×(-3)=-49.
⑵由a1=-5,d =-9-(-5)=-4,得此数列的通项公式为an=-5-4(n-1).
由-401=-5-4(n-1),得n=100,
即-401是这个数列的第100项.
1、已知等差数列的首项与公差,可求得其任何一项;
2、在等差数列的通项公式中,a1,d,n,an四个量中知三求一.
结论
跟踪训练
3.等差中项
如果 a, A, b 成等差数列,那么 A 叫做 a 与 b 的等差中项 .
由等差中项的定义可知, a, A, b 满足关系:
意义:
任意两个数都有等差中项,并且这个等差中项是唯一的.当 a=b 时,A = a = b .
例2.在-1与7之间顺次插入三个数a,b,c使这五个数成等差数列,求此数列.
思考:(1)在等差数列{an}中,是否有
(2)在数列{an}中,如果对于任意的正整数n(n≥2),都有
那么数列{an}一定是等差数列吗?
是
是
由此可证明一个数列为等差数列。
4、等差数列通项公式的推广
解析:
由等差数列的通项公式得
解法一: 依题意得:
a1+2d=9
a1+8d=3
解之得 a1 =11
d =-1∴这个数列的通项公式是:an=11- (n-1)=12-n
故 a12= 0, a 3n = 12 – 3 n.
解法二:
你能用七巧板拼成一幅有意义的图形吗?并写出解说词.
例如:
帆船 乘风破浪会有时
生命在于运动
2.2 等差数列
第二课时
2、等差数列的通项公式
1、等差数列的定义
3、等差数列的中项
复习
通项公式的证明及推广
100与180
5、等差数列的通项及图象特征
解析:
思考
结论:
首项是1,公差是2的无穷等差数列的通项公式为
an =2n-1
相应的图象是直线y=2x-1上均匀排开的无穷多个孤立的点,如右图
例如:
【思路点拨】 将递推公式变形,然后按等差数列的定义判定.
有些数列若通过取倒数代数变形方法,可由复杂变为简单,使问题得以解决.
例7 小明、小明的爸爸和小明的爷爷三个人的年龄恰好构成一个等差数列,他们三人的年龄之和为120岁,小明爷爷的年龄比小明年龄的4倍还多
5岁,求他们祖孙三人的年龄.
解 设小明、小明的爸爸和小明的爷爷的年龄分别为
,其中
为公差.
则:
解得:
,
从而
,
将成等差数列的三个数
是经常使用的方法.
设为
例8、成等差数列的四个数之和为26,第二个与第三个数之积为40,求这四个数。
四个数等差的设法:
a-3d,a-d,a+d,a+3d
公差为2d。
解:设三个数为a-d,a,a+d,则
解之得
故所求三数依次为2,4,6或6,4,2
等差数列的设法及求解
(1)若有三个数成等差数列,则一般设为a-d,a,a+d;
(2)若有四个数成等差数列,则一般设为a-3d,a-d,a+d,a+3d;
(3)若有五个数成等差数列,则一般设为a-2d,a-d,a,a+d,a+2d.
例9
例10 如图,三个正方形的边AB,BC,CD的长组成等差数列,且AD=21cm,这三个正方形的面积之和是179cm2.
(1)求AB,BC,CD的长;
(2)以 AB,BC,CD的长为等差数列的前三项,以第9项为边长的正方形的面积是多少?
3,7,11
a9=35
S9=1225
国王在处决犯人,并使用一种特殊的方式:让犯人说一句话,如果犯人说的是真话,那么就绞死;如果犯人说的是假话,那么斩首。轮到一个聪明的犯人时,他说:“我说的是假话。”这样的话,就产生了悖论,即如果他说的是假话,那么这句话说明自己说的是真话。反过来,如果这句话是真话,那么这句话又说明他说的是假话。这样就没办法判断真假了。大臣们都很为难。国王想了想,叫人找来一个大盒子,把这个人放到盒子里,并注入毒气。国王说:“在我打开盒子前,他既是生的又是死的。
2.2.2 等差数列的性质
第一课时
2、等差数列的通项公式
1、等差数列的定义
3、等差数列的中项
复习
通项公式的证明及推广
4、通项公式法:
5、等差数列的性质
已知数列 为等差数列,那么有
性质1:若 成等差数列,则
成等差数列.
证明:根据等差数列的定义,
即 成等差数列.
如 成等差数列, 成等差数列.
推广:下标成等差的项,按原顺序可排成新的等差数列。(如奇数项,项数是7的倍数的项)
反之不成立:常数列
性质2:设 若 则
反之不成立:常数列
①若 为等差数列,且正整数p、q、r满足 ,则一定有:
性质2的推论:
③除首末两项以外,每一项是其左右相邻两项的等差中项。
②在有穷等差数列中,与首末两项等距离的两项之和等于首末两项之和。
39
15
性质3:设 c, b 为常数,若数列 为等差数列,则数
列 为等差数列.
反之不成立:c=0
性质4:设 p, q 为常数,若数列 、 均为等差数列,
则数列 为等差数列.
反之不成立:p,q互为相反数,两个数列相同,但非等差。
2023
7
4
(1)(2010年高考大纲全国卷Ⅱ)如果等差数列{an}中,a3+a4+a5=12,那么a1+a2+…+a7=( )
A.14 B.21
C.28 D.35
(2)已知等差数列{an},若a11=-26,a51=54,则a14=________.
例1
【思路点拨】 利用等差数列的性质求解,或整体考虑问题.(1)利用2a4=a3+a5,(2)利用an=am+(n-m)d.
【答案】 (1)C (2)-20
变式训练1 (1)数列{an}中,a3、a10是方程x2-3x-5=0的两根,若{an}是等差数列,则a5+a8=________;
(2)在等差数列{an}中,已知a1-a4-a8-a12+a15=2,则a3+a13=________.
解析:(1)由根与系数的关系知a3+a10=3,
故a5+a8=a3+a10=3.
(2)由a1+a15=a4+a12,
得a8=-2,∴a3+a13=2a8=-4.
答案:(1)3 (2)-4
等差数列的应用题
某公司经销一种数码产品,第1年可获利200万元.从第2年起,由于市场竞争等方面的原因,其利润每年比上一年减少20万元,按照这一规律,如果公司不开发新产品,也不调整经营策略,从哪一年起,该公司经销这一产品将亏损?
例3
【解】 由题设可知第1年获利200万元,第2年获利180万元,第3年获利160万元,….
设从第1年起,第n年的利润为an,则an-an-1=-20,n≥2,n∈N*.所以每年的利润可构成一个等差数列{an},且首项a1=200,公差d=-20.
所以an=a1+(n-1)d=220-20n.
若an<0,则该公司经销这一产品将亏损,
所以由an=220-20n<0,得n>11,
即从第12年起,该公司经销此产品将亏损.
【名师点评】 “亏损”=“利润小于零”.由于公差d<0,所以利润构成的数列是一个递减数列,即随着n的增大,an的值越来越小,an<0时(此处暗含an-1≥0成立)公司将出现亏损.
变式训练2 夏季高山上的温度从山脚起,每升高100 m,平均降低0.7 ℃,已知山顶处的温度是14.8 ℃,山脚处的温度为26 ℃,问此山相对于山脚的高度是多少?
解:∵每升高100 m温度降低0.7 ℃,
∴该处温度的变化是一个等差数列问题.
山脚温度为首项a1=26,山顶温度为末项an=14.8,
∴26+(n-1)×(-0.7)=14.8,解得n=17,
∴此山的高度为(17-1)×100=1600(m).
方法感悟
(4)若{an}是有穷等差数列,则与首、末两项等距离的两项之和都相等,且等于首、末两项之和,即a1+an=a2+an-1=…=ai+1+an-i=….
(5)数列{λan+b}(λ、b是常数)是公差为λd的等差数列.
等差数列的性质与判定
第二章
数 列
第四课时:
课题
1、等差数列的概念;
2、等差中项的概念;
3、等差数列的通项公式;
或
从第二项起,每一项与前一项的差是同一个常数
1、若 为公差为 有穷等差数列,则把 倒序
排列的数列仍然是等差数列,公差为 。
2、若 为等差数列,则等间隔抽取的子数列
也是等差数列。即脚码等差,项就等差。
3、若 、 是公差分别为 的等差数列,则 、 、 仍为等差数列,公差分别为
4、等差数列的首项为 ,公差 ,
将前 项去掉,其余各项组成的数列仍然是等差数列。新数列的首项为 公差仍为 。
①若 为等差数列,且正整数p、q、r满足 ,则一定有:
性质5的推论:
5、若 为等差数列,且正整数p、q、r、s满足 ,则一定有:
你能证明么?
③除首末两项以外,每一项是其左右相邻两项的等差中项。
②在有穷等差数列中,与首末两项等距离的两项之和等于首末两项之和。
39
15
- 4
A
D
98
2023
7
4
1、定义法:
证明后一项与前一项的差是与n无关的常数:
2、等差中项法:
证明第n项是第n-1项与第n+1项的等差中项:
3、通项公式法:
证明数列的通项是关于n的一次函数。
1、等差数列的性质;
2、等差数列的判定;
3、等差数列的图像与单调性。
定义法:
等差中项法:
通项公式法:
新知探究
思考:
等差数列性质1
等差数列性质1
【例1】
性质2:等差中项
【思考】若在a, b中插入一个数A,使a,A,b成等差数列,则A应满足什么条件?
【练习】
1.数列1,3,5,7,9,11,13……
中7是那些项的等差中项?
2.求下列两个数的等差中项:
(1)30与18; (2)-13与9。
3.在-1与9之间顺次插入a,b,c三
个数,使这五个数成等差数列,
求插入的三个数和等差数列的公差?
在学习了等差中项的概念后,我们又多了一中判定等差数列的方法。
问:如何判断一个数列为等差数列
【例2】已知a,b,c依次成等差数列,
求证: 成等差
数列.
【例3】
性质3:
数列{an}是等差数列,m、n、p、q∈N+,且m+n=p+q,则am+an=ap+aq。
判断:
说明:1.可推广到三项,四项等
2.等式两边作和的项数必须一样多
3.特别地:m+n=2p则am+an=2ap
性质1:公差计算公式,通项公式二
课后小结
性质2:等差中项
性质3:下标和性质
1、定义:
2、 通项公式:
推广:
一、知识要点;
5.等差数列性质:
(1)
(2)
若
则
(3)若数列 是等差数列,则
也是等差数列
(4)等差数列{an}的任意等距离的项构成的数列
仍为等差数列
6.等差数列判定方法:
(1)定义法:
(2)递推公式法:
(3)看通项法:
(4)看前n项和法:
二、主要题型分析:
更多资源xiti123.
5. 已知 是两个等差数列,前 项和
分别是 和 且
求
在等差数列
中,
为公差,若
且
求证:
证明: 设首项为
,则
例2.
等差数列的性质
P3911
am+an=ap+aq
②上面的命题中的等式两边有 相 同 数 目
的项,否则不成立。如a1+a2=a3 成立吗?
【说明】
3.更一般的情形,an= ,d=
1. {an}为等差数列
2. a、b、c成等差数列
an+1- an=d
an+1=an+d
an= a1+(n-1) d
an= kn + b
(k、b为常数)
am+(n - m) d
b为a、c 的等差中项
2b= a+c
4.在等差数列{an}中,由 m+n=p+q
注意:①上面的命题的逆命题 是不一定成立 的;
等差数列的性质
P398,10
5. 在等差数列{an}中a1+an a2+ an-1 a3+ an-2 …
=
=
=
例2 .在等差数列{an}中
(1) 已知 a6+a9+a12+a15=20,求a1+a20
(2)已知 a3+a11=10,求 a6+a7+a8
(3) 已知 a4+a5+a6+a7=56,a4a7=187,求a14及公差d.
分析:由 a1+a20 =a6+ a15 = a9 +a12 及 a6+a9+a12+a15=20,可得a1+a20=10
分析: a3+a11 =a6+a8 =2a7 ,又已知 a3+a11=10,
∴ a6+a7+a8= (a3+a11)=15
分析: a4+a5+a6+a7=56 a4+a7=28 ①
又 a4a7=187 ② , 解 ①、 ② 得
a4= 17
a7= 11
a4= 11
a7= 17
或
∴d= _2或2, 从而a14= _3或31
例题分析
1.一个首项为23,公差为整数的等差数列,如果前六项均为正数,第七项起为负数,则它的公差是多少?
解:由题意得,
a6=a1+5d>0 a7=a1+6d<0
2.已知等差数列{an}的首项为30,这个数列从第12项起为负数,求公差d的范围。
解:a12=30+11d<0
a11=30+10d≥0
∵d∈Z ∴d=-4
∴-23/5<d<-23/6
∴ -3≤d<-30/11
即公差d的范围为:-3≤d<-30/11
7.{an} 、{bn}是项数相同的等差数列,则{Pan +qbn} 是等差数列
3.通项公式推广 an= ,d=
本节课小结
1. {an}为等差数列
2. a、b、c成等差数列
an+1- an=d
an= a1+(n-1) d
an= kn + b
(k、b为常数)
am+(n - m) d
b为a、c 的等差中项AA
2b= a+c
4.在等差数列{an}中,由 m+n=p+q
am+an=ap+aq
5. 特别的有:a1+an a2+ an-1 a3+ an-2 …
=
=
=
6. am , am+k , am+2k , am+3k … 成等差数列。
等差中项
如果三个数x,A,y组成等差数列,那么A叫做x和y的等差中项。
如果A是x和y的等差中项,则
在一个等差数列中,从第2项起,每一项(有穷数列的末项除外)都是它的前一项与后一项的等差中项。
性质1
例3.已知等差数列的公差为d,第m项为am,试求其第n项an.
解:由等差数列的通项公式可知
an=a1+(n-1)d,am=a1+(m-1)d,
两式相减得,
an=am+(n-m)d.
性质2
例4.(1)在等差数列{an}中,若m+n=p+q,
求证:am+an=ap+aq.
(2)在等差数列{an}中,若a3+a4+a5+a6+a7=450,求a2+a8.
解:(2)∵ a2+a8=a3+a7=a4+a6=2a5,
∴ 5a5=450, a5=90,
∴ a2+a8= 2×90=180.
(性质3)
例6.已知等差数列{an}的首项a1=17,公差d=-0.6,此等差数列从第几项开始出现负数?
解:由题意,{an}的通项公式是
an=17-0.6(n-1),
令17-0.6(n-1)<0,解得
又因为{an}是递减数列,
所以数列{an}从第30项起开始出现负数。
例8
(1)已知等差数列{an}中, a3 +a15=30,求a9, a7+a11
解:
(1)∵a9是a3和a15的等差中项
∴
(2)已知等差数列{an}中, a3 +a4+a5 +a6 +a7=150,求a2+a8的值
∵7+11=3+15
(2)∵3+7=4+6=5+5
∴ a3 +a4+a5 +a6 +a7=5 a5=150
即a5=30
故a2+a8 =2 a5=60
∴ a7+a11 =a3 +a15=30
∴ a3+a7 =a4 +a6=2 a5
(1)等差数列{an}中,a3 +a9+a15+a21=8,则a12 =
(2)已知等差数列{an}中, a3 和a15是方程x2-6x-1=0的两个根,则a7 +a8 +a9+a10+a11=
2
(3)已知等差数列{an}中, a3 +a5= -14, 2a2+a6 = -15,则a8=
-19
跟踪训练
鸡蛋,从外打破是食物,从内打破是生命。人生亦是,从外打破是压力,从内打破是成长。如果你等待别人从外打破你,那么你注定成为别人的食物;如果能让自己从内打破,那么你会发现自己的成长相当于一种重生。
2.2 等差数列
第一课时
一、数列的定义,通项公式:
按一定次序排成的一列数叫做数列。一般写成a1,a2,a3 ,… an,…
如果数列{an}的第n项an与n的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式。
二、数列的简单表示:
三、给出数列的方法:
www.
复习
在过去的三百多年里,人们分别在下列时间里观测到了哈雷慧星:
(1)1682,1758,1834,1910,1986,( )
你能预测出下一次的大致时间吗?
2062
相差76
某此系统抽样所抽取的样本号分别是:
7,19,31,43,55,67,79,91,103,115.
某长跑运动员7天里每天的训练量(单位:m)是:
7500,8000,8500,9000,10000,10500.
(观察以下数列)
引入
这三个数列有何共同特征
从第2项起,每一项与其前一项之差等于同一个常数。
请尝试着给具有上述特征的特殊数列
用数学的语言下定义
交流
1、等差数列的定义
如果一个数列从第2项起,每一项与其前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母d表示。
(1)指出定义中的关键词:
从第2项起
等于同一个常数
⑵由定义得等差数列的递推公式:
说明:此公式是判断、证明一个数列是否为等差数列的主要依据.
每一项与其前一项的差
探究
练习:判断下列数列中哪些是等差数列,哪些不是?如果是,写出首项a1和公差d, 如果不是,说明理由。
www.
(6)
2、等差数列的通项公式
根据等差数列的定义得到
方法一:不完全归纳法
2、等差数列的通项公式
将所有等式相加得
方法二
累加法
例1 ⑴求等差数列8,5,2,…的第20项.
⑵- 401是不是等差数列-5,-9,-13,…的项?如果是,是第几项?
解:
⑴由a1=8,d=5-8=-3,n=20,得
a20=8+(20-1) ×(-3)=-49.
⑵由a1=-5,d =-9-(-5)=-4,得此数列的通项公式为an=-5-4(n-1).
由-401=-5-4(n-1),得n=100,
即-401是这个数列的第100项.
1、已知等差数列的首项与公差,可求得其任何一项;
2、在等差数列的通项公式中,a1,d,n,an四个量中知三求一.
结论
跟踪训练
3.等差中项
如果 a, A, b 成等差数列,那么 A 叫做 a 与 b 的等差中项 .
由等差中项的定义可知, a, A, b 满足关系:
意义:
任意两个数都有等差中项,并且这个等差中项是唯一的.当 a=b 时,A = a = b .
例2.在-1与7之间顺次插入三个数a,b,c使这五个数成等差数列,求此数列.
思考:(1)在等差数列{an}中,是否有
(2)在数列{an}中,如果对于任意的正整数n(n≥2),都有
那么数列{an}一定是等差数列吗?
是
是
由此可证明一个数列为等差数列。
4、等差数列通项公式的推广
解析:
由等差数列的通项公式得
解法一: 依题意得:
a1+2d=9
a1+8d=3
解之得 a1 =11
d =-1∴这个数列的通项公式是:an=11- (n-1)=12-n
故 a12= 0, a 3n = 12 – 3 n.
解法二:
你能用七巧板拼成一幅有意义的图形吗?并写出解说词.
例如:
帆船 乘风破浪会有时
生命在于运动
2.2 等差数列
第二课时
2、等差数列的通项公式
1、等差数列的定义
3、等差数列的中项
复习
通项公式的证明及推广
100与180
5、等差数列的通项及图象特征
解析:
思考
结论:
首项是1,公差是2的无穷等差数列的通项公式为
an =2n-1
相应的图象是直线y=2x-1上均匀排开的无穷多个孤立的点,如右图
例如:
【思路点拨】 将递推公式变形,然后按等差数列的定义判定.
有些数列若通过取倒数代数变形方法,可由复杂变为简单,使问题得以解决.
例7 小明、小明的爸爸和小明的爷爷三个人的年龄恰好构成一个等差数列,他们三人的年龄之和为120岁,小明爷爷的年龄比小明年龄的4倍还多
5岁,求他们祖孙三人的年龄.
解 设小明、小明的爸爸和小明的爷爷的年龄分别为
,其中
为公差.
则:
解得:
,
从而
,
将成等差数列的三个数
是经常使用的方法.
设为
例8、成等差数列的四个数之和为26,第二个与第三个数之积为40,求这四个数。
四个数等差的设法:
a-3d,a-d,a+d,a+3d
公差为2d。
解:设三个数为a-d,a,a+d,则
解之得
故所求三数依次为2,4,6或6,4,2
等差数列的设法及求解
(1)若有三个数成等差数列,则一般设为a-d,a,a+d;
(2)若有四个数成等差数列,则一般设为a-3d,a-d,a+d,a+3d;
(3)若有五个数成等差数列,则一般设为a-2d,a-d,a,a+d,a+2d.
例9
例10 如图,三个正方形的边AB,BC,CD的长组成等差数列,且AD=21cm,这三个正方形的面积之和是179cm2.
(1)求AB,BC,CD的长;
(2)以 AB,BC,CD的长为等差数列的前三项,以第9项为边长的正方形的面积是多少?
3,7,11
a9=35
S9=1225
国王在处决犯人,并使用一种特殊的方式:让犯人说一句话,如果犯人说的是真话,那么就绞死;如果犯人说的是假话,那么斩首。轮到一个聪明的犯人时,他说:“我说的是假话。”这样的话,就产生了悖论,即如果他说的是假话,那么这句话说明自己说的是真话。反过来,如果这句话是真话,那么这句话又说明他说的是假话。这样就没办法判断真假了。大臣们都很为难。国王想了想,叫人找来一个大盒子,把这个人放到盒子里,并注入毒气。国王说:“在我打开盒子前,他既是生的又是死的。
2.2.2 等差数列的性质
第一课时
2、等差数列的通项公式
1、等差数列的定义
3、等差数列的中项
复习
通项公式的证明及推广
4、通项公式法:
5、等差数列的性质
已知数列 为等差数列,那么有
性质1:若 成等差数列,则
成等差数列.
证明:根据等差数列的定义,
即 成等差数列.
如 成等差数列, 成等差数列.
推广:下标成等差的项,按原顺序可排成新的等差数列。(如奇数项,项数是7的倍数的项)
反之不成立:常数列
性质2:设 若 则
反之不成立:常数列
①若 为等差数列,且正整数p、q、r满足 ,则一定有:
性质2的推论:
③除首末两项以外,每一项是其左右相邻两项的等差中项。
②在有穷等差数列中,与首末两项等距离的两项之和等于首末两项之和。
39
15
性质3:设 c, b 为常数,若数列 为等差数列,则数
列 为等差数列.
反之不成立:c=0
性质4:设 p, q 为常数,若数列 、 均为等差数列,
则数列 为等差数列.
反之不成立:p,q互为相反数,两个数列相同,但非等差。
2023
7
4
(1)(2010年高考大纲全国卷Ⅱ)如果等差数列{an}中,a3+a4+a5=12,那么a1+a2+…+a7=( )
A.14 B.21
C.28 D.35
(2)已知等差数列{an},若a11=-26,a51=54,则a14=________.
例1
【思路点拨】 利用等差数列的性质求解,或整体考虑问题.(1)利用2a4=a3+a5,(2)利用an=am+(n-m)d.
【答案】 (1)C (2)-20
变式训练1 (1)数列{an}中,a3、a10是方程x2-3x-5=0的两根,若{an}是等差数列,则a5+a8=________;
(2)在等差数列{an}中,已知a1-a4-a8-a12+a15=2,则a3+a13=________.
解析:(1)由根与系数的关系知a3+a10=3,
故a5+a8=a3+a10=3.
(2)由a1+a15=a4+a12,
得a8=-2,∴a3+a13=2a8=-4.
答案:(1)3 (2)-4
等差数列的应用题
某公司经销一种数码产品,第1年可获利200万元.从第2年起,由于市场竞争等方面的原因,其利润每年比上一年减少20万元,按照这一规律,如果公司不开发新产品,也不调整经营策略,从哪一年起,该公司经销这一产品将亏损?
例3
【解】 由题设可知第1年获利200万元,第2年获利180万元,第3年获利160万元,….
设从第1年起,第n年的利润为an,则an-an-1=-20,n≥2,n∈N*.所以每年的利润可构成一个等差数列{an},且首项a1=200,公差d=-20.
所以an=a1+(n-1)d=220-20n.
若an<0,则该公司经销这一产品将亏损,
所以由an=220-20n<0,得n>11,
即从第12年起,该公司经销此产品将亏损.
【名师点评】 “亏损”=“利润小于零”.由于公差d<0,所以利润构成的数列是一个递减数列,即随着n的增大,an的值越来越小,an<0时(此处暗含an-1≥0成立)公司将出现亏损.
变式训练2 夏季高山上的温度从山脚起,每升高100 m,平均降低0.7 ℃,已知山顶处的温度是14.8 ℃,山脚处的温度为26 ℃,问此山相对于山脚的高度是多少?
解:∵每升高100 m温度降低0.7 ℃,
∴该处温度的变化是一个等差数列问题.
山脚温度为首项a1=26,山顶温度为末项an=14.8,
∴26+(n-1)×(-0.7)=14.8,解得n=17,
∴此山的高度为(17-1)×100=1600(m).
方法感悟
(4)若{an}是有穷等差数列,则与首、末两项等距离的两项之和都相等,且等于首、末两项之和,即a1+an=a2+an-1=…=ai+1+an-i=….
(5)数列{λan+b}(λ、b是常数)是公差为λd的等差数列.
等差数列的性质与判定
第二章
数 列
第四课时:
课题
1、等差数列的概念;
2、等差中项的概念;
3、等差数列的通项公式;
或
从第二项起,每一项与前一项的差是同一个常数
1、若 为公差为 有穷等差数列,则把 倒序
排列的数列仍然是等差数列,公差为 。
2、若 为等差数列,则等间隔抽取的子数列
也是等差数列。即脚码等差,项就等差。
3、若 、 是公差分别为 的等差数列,则 、 、 仍为等差数列,公差分别为
4、等差数列的首项为 ,公差 ,
将前 项去掉,其余各项组成的数列仍然是等差数列。新数列的首项为 公差仍为 。
①若 为等差数列,且正整数p、q、r满足 ,则一定有:
性质5的推论:
5、若 为等差数列,且正整数p、q、r、s满足 ,则一定有:
你能证明么?
③除首末两项以外,每一项是其左右相邻两项的等差中项。
②在有穷等差数列中,与首末两项等距离的两项之和等于首末两项之和。
39
15
- 4
A
D
98
2023
7
4
1、定义法:
证明后一项与前一项的差是与n无关的常数:
2、等差中项法:
证明第n项是第n-1项与第n+1项的等差中项:
3、通项公式法:
证明数列的通项是关于n的一次函数。
1、等差数列的性质;
2、等差数列的判定;
3、等差数列的图像与单调性。
定义法:
等差中项法:
通项公式法:
新知探究
思考:
等差数列性质1
等差数列性质1
【例1】
性质2:等差中项
【思考】若在a, b中插入一个数A,使a,A,b成等差数列,则A应满足什么条件?
【练习】
1.数列1,3,5,7,9,11,13……
中7是那些项的等差中项?
2.求下列两个数的等差中项:
(1)30与18; (2)-13与9。
3.在-1与9之间顺次插入a,b,c三
个数,使这五个数成等差数列,
求插入的三个数和等差数列的公差?
在学习了等差中项的概念后,我们又多了一中判定等差数列的方法。
问:如何判断一个数列为等差数列
【例2】已知a,b,c依次成等差数列,
求证: 成等差
数列.
【例3】
性质3:
数列{an}是等差数列,m、n、p、q∈N+,且m+n=p+q,则am+an=ap+aq。
判断:
说明:1.可推广到三项,四项等
2.等式两边作和的项数必须一样多
3.特别地:m+n=2p则am+an=2ap
性质1:公差计算公式,通项公式二
课后小结
性质2:等差中项
性质3:下标和性质
1、定义:
2、 通项公式:
推广:
一、知识要点;
5.等差数列性质:
(1)
(2)
若
则
(3)若数列 是等差数列,则
也是等差数列
(4)等差数列{an}的任意等距离的项构成的数列
仍为等差数列
6.等差数列判定方法:
(1)定义法:
(2)递推公式法:
(3)看通项法:
(4)看前n项和法:
二、主要题型分析:
更多资源xiti123.
5. 已知 是两个等差数列,前 项和
分别是 和 且
求
在等差数列
中,
为公差,若
且
求证:
证明: 设首项为
,则
例2.
等差数列的性质
P3911
am+an=ap+aq
②上面的命题中的等式两边有 相 同 数 目
的项,否则不成立。如a1+a2=a3 成立吗?
【说明】
3.更一般的情形,an= ,d=
1. {an}为等差数列
2. a、b、c成等差数列
an+1- an=d
an+1=an+d
an= a1+(n-1) d
an= kn + b
(k、b为常数)
am+(n - m) d
b为a、c 的等差中项
2b= a+c
4.在等差数列{an}中,由 m+n=p+q
注意:①上面的命题的逆命题 是不一定成立 的;
等差数列的性质
P398,10
5. 在等差数列{an}中a1+an a2+ an-1 a3+ an-2 …
=
=
=
例2 .在等差数列{an}中
(1) 已知 a6+a9+a12+a15=20,求a1+a20
(2)已知 a3+a11=10,求 a6+a7+a8
(3) 已知 a4+a5+a6+a7=56,a4a7=187,求a14及公差d.
分析:由 a1+a20 =a6+ a15 = a9 +a12 及 a6+a9+a12+a15=20,可得a1+a20=10
分析: a3+a11 =a6+a8 =2a7 ,又已知 a3+a11=10,
∴ a6+a7+a8= (a3+a11)=15
分析: a4+a5+a6+a7=56 a4+a7=28 ①
又 a4a7=187 ② , 解 ①、 ② 得
a4= 17
a7= 11
a4= 11
a7= 17
或
∴d= _2或2, 从而a14= _3或31
例题分析
1.一个首项为23,公差为整数的等差数列,如果前六项均为正数,第七项起为负数,则它的公差是多少?
解:由题意得,
a6=a1+5d>0 a7=a1+6d<0
2.已知等差数列{an}的首项为30,这个数列从第12项起为负数,求公差d的范围。
解:a12=30+11d<0
a11=30+10d≥0
∵d∈Z ∴d=-4
∴-23/5<d<-23/6
∴ -3≤d<-30/11
即公差d的范围为:-3≤d<-30/11
7.{an} 、{bn}是项数相同的等差数列,则{Pan +qbn} 是等差数列
3.通项公式推广 an= ,d=
本节课小结
1. {an}为等差数列
2. a、b、c成等差数列
an+1- an=d
an= a1+(n-1) d
an= kn + b
(k、b为常数)
am+(n - m) d
b为a、c 的等差中项AA
2b= a+c
4.在等差数列{an}中,由 m+n=p+q
am+an=ap+aq
5. 特别的有:a1+an a2+ an-1 a3+ an-2 …
=
=
=
6. am , am+k , am+2k , am+3k … 成等差数列。
等差中项
如果三个数x,A,y组成等差数列,那么A叫做x和y的等差中项。
如果A是x和y的等差中项,则
在一个等差数列中,从第2项起,每一项(有穷数列的末项除外)都是它的前一项与后一项的等差中项。
性质1
例3.已知等差数列的公差为d,第m项为am,试求其第n项an.
解:由等差数列的通项公式可知
an=a1+(n-1)d,am=a1+(m-1)d,
两式相减得,
an=am+(n-m)d.
性质2
例4.(1)在等差数列{an}中,若m+n=p+q,
求证:am+an=ap+aq.
(2)在等差数列{an}中,若a3+a4+a5+a6+a7=450,求a2+a8.
解:(2)∵ a2+a8=a3+a7=a4+a6=2a5,
∴ 5a5=450, a5=90,
∴ a2+a8= 2×90=180.
(性质3)
例6.已知等差数列{an}的首项a1=17,公差d=-0.6,此等差数列从第几项开始出现负数?
解:由题意,{an}的通项公式是
an=17-0.6(n-1),
令17-0.6(n-1)<0,解得
又因为{an}是递减数列,
所以数列{an}从第30项起开始出现负数。
例8
(1)已知等差数列{an}中, a3 +a15=30,求a9, a7+a11
解:
(1)∵a9是a3和a15的等差中项
∴
(2)已知等差数列{an}中, a3 +a4+a5 +a6 +a7=150,求a2+a8的值
∵7+11=3+15
(2)∵3+7=4+6=5+5
∴ a3 +a4+a5 +a6 +a7=5 a5=150
即a5=30
故a2+a8 =2 a5=60
∴ a7+a11 =a3 +a15=30
∴ a3+a7 =a4 +a6=2 a5
(1)等差数列{an}中,a3 +a9+a15+a21=8,则a12 =
(2)已知等差数列{an}中, a3 和a15是方程x2-6x-1=0的两个根,则a7 +a8 +a9+a10+a11=
2
(3)已知等差数列{an}中, a3 +a5= -14, 2a2+a6 = -15,则a8=
-19
跟踪训练
