5.4圆环的面积(课件) 人教版数学六年级上册(共16张PPT)
文档属性
| 名称 | 5.4圆环的面积(课件) 人教版数学六年级上册(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-14 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
简单的排列问题
使学生经历观察、比较、分析等数学活动过程,探索并掌握圆环的面积公式,能正确计算圆环的面积,解决简单的实际问题。
使学生进一步提高运用已有知识解决新问题的能力,发展空间观念和初步的推理能力。
了解现实生活中有许多与圆环的面积有关的问题,获得运用知识解决问题的成功体验。
你从中读出哪些数学信息?
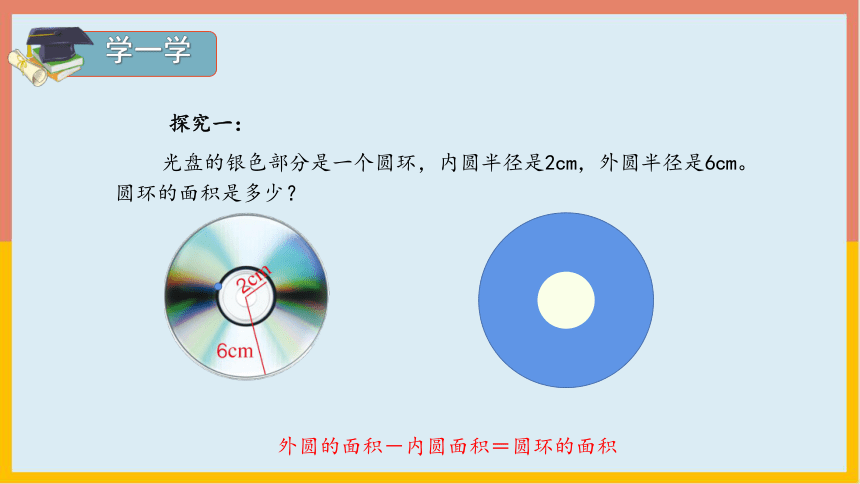
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
新课导入
课前活动一:
讨论交流:
观看微课《圆环的面积》,举例说说圆环的面积的计算方法,归纳总结后,交流互评。
课前活动
课前活动二:
下面圆环的面积是多少平方厘米?
=3.14×102
3.14×62
-
=3.14×100
-
3.14×36
=200.96(平方厘米)
答:这个圆环的面积是200.96平方厘米。
-
3.14×
( )
2
20
2
3.14×
( )
2
12
2
课前活动
与你的小伙伴交流你的做法、以及你的思考。
探究一:
外圆的面积-内圆面积=圆环的面积
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
学一学
3.14×6 -3.14×2
=113.04-12.56
=100.48(cm )
答:圆环的面积是100.48 cm 。
探究一:
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
3.14×(6 -2 )
=3.14×32
=100.48(cm )
答:圆环的面积是100.48 cm 。
探究二:
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
50÷2=25(m)
10÷2=5(m)
答:草坪的占地面积是1884m 。
一个圆形环岛的直径是50m,中间是一个直径为10m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
3.14×(25 -5 )
=3.14×600
=1884(m )
1.一块玉璧,外直径18厘米,内直径7厘米。这块玉璧的面积是多少?
18÷2=9(cm)
7÷2=3.5(cm)
答:这块玉璧的面积是215.875cm 。
3.14×(9 -3.5 )
=3.14×68.75
=215.875(cm )
2.计算下面圆环的面积。
答:这圆环的面积是251.2cm 。
3.14×(12 -8 )
=3.14×80
=251.2(cm )
3.一座土楼的外直径34米,内直径14米;另外一座外直径26米,内直径也是14米。两座土楼的房屋的占地面积相差多少?
3.14×【(34÷2) -(14÷2) 】-3.14×【(26÷2) -(14÷2) 】
=3.14×240-3.14×120
=376.8(cm )
3.14×(30÷2+5)2
= 3.14×202
= 1256(平方米)
1256-706.5 = 549.5(平方米)
3.14×(30÷2)2
= 3.14×152
= 706.5(平方米)
扩建前面积:
扩建后面积:
答:扩建后旱冰场的面积增加了549.5平方米。
4.一个圆形旱冰场的直径是30米,扩建后半径增加了5米。
扩建后旱冰场的面积增加了多少平方米?
1.圆环的面积=外圆的面积-内圆的面积。
2.用字母表示为:S圆环=π(R2-r2)
3.也可以表示为:S圆环=πR2-πr
圆环的面积
课堂小结
1.完成《圆环的面积课后作业》;
2.讨论交流:
观看微课《解决生活中圆的问题》,举例说说解决生活中圆的问题的方法,归纳总结后,交流互评。
作业布置
再见
简单的排列问题
使学生经历观察、比较、分析等数学活动过程,探索并掌握圆环的面积公式,能正确计算圆环的面积,解决简单的实际问题。
使学生进一步提高运用已有知识解决新问题的能力,发展空间观念和初步的推理能力。
了解现实生活中有许多与圆环的面积有关的问题,获得运用知识解决问题的成功体验。
你从中读出哪些数学信息?
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
新课导入
课前活动一:
讨论交流:
观看微课《圆环的面积》,举例说说圆环的面积的计算方法,归纳总结后,交流互评。
课前活动
课前活动二:
下面圆环的面积是多少平方厘米?
=3.14×102
3.14×62
-
=3.14×100
-
3.14×36
=200.96(平方厘米)
答:这个圆环的面积是200.96平方厘米。
-
3.14×
( )
2
20
2
3.14×
( )
2
12
2
课前活动
与你的小伙伴交流你的做法、以及你的思考。
探究一:
外圆的面积-内圆面积=圆环的面积
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
学一学
3.14×6 -3.14×2
=113.04-12.56
=100.48(cm )
答:圆环的面积是100.48 cm 。
探究一:
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
3.14×(6 -2 )
=3.14×32
=100.48(cm )
答:圆环的面积是100.48 cm 。
探究二:
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
50÷2=25(m)
10÷2=5(m)
答:草坪的占地面积是1884m 。
一个圆形环岛的直径是50m,中间是一个直径为10m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
3.14×(25 -5 )
=3.14×600
=1884(m )
1.一块玉璧,外直径18厘米,内直径7厘米。这块玉璧的面积是多少?
18÷2=9(cm)
7÷2=3.5(cm)
答:这块玉璧的面积是215.875cm 。
3.14×(9 -3.5 )
=3.14×68.75
=215.875(cm )
2.计算下面圆环的面积。
答:这圆环的面积是251.2cm 。
3.14×(12 -8 )
=3.14×80
=251.2(cm )
3.一座土楼的外直径34米,内直径14米;另外一座外直径26米,内直径也是14米。两座土楼的房屋的占地面积相差多少?
3.14×【(34÷2) -(14÷2) 】-3.14×【(26÷2) -(14÷2) 】
=3.14×240-3.14×120
=376.8(cm )
3.14×(30÷2+5)2
= 3.14×202
= 1256(平方米)
1256-706.5 = 549.5(平方米)
3.14×(30÷2)2
= 3.14×152
= 706.5(平方米)
扩建前面积:
扩建后面积:
答:扩建后旱冰场的面积增加了549.5平方米。
4.一个圆形旱冰场的直径是30米,扩建后半径增加了5米。
扩建后旱冰场的面积增加了多少平方米?
1.圆环的面积=外圆的面积-内圆的面积。
2.用字母表示为:S圆环=π(R2-r2)
3.也可以表示为:S圆环=πR2-πr
圆环的面积
课堂小结
1.完成《圆环的面积课后作业》;
2.讨论交流:
观看微课《解决生活中圆的问题》,举例说说解决生活中圆的问题的方法,归纳总结后,交流互评。
作业布置
再见
