2.2.3直线与平面平行的性质
文档属性
| 名称 | 2.2.3直线与平面平行的性质 |  | |
| 格式 | zip | ||
| 文件大小 | 387.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-23 09:07:18 | ||
图片预览








文档简介
(共69张PPT)
2.2.3直线与平面
平行的性质
复习引入
1.直线与直线的位置关系有哪几种?
复习引入
1.直线与直线的位置关系有
共面
异面
平行
相交
复习引入
1.直线与直线的位置关系有
共面
异面
平行
相交
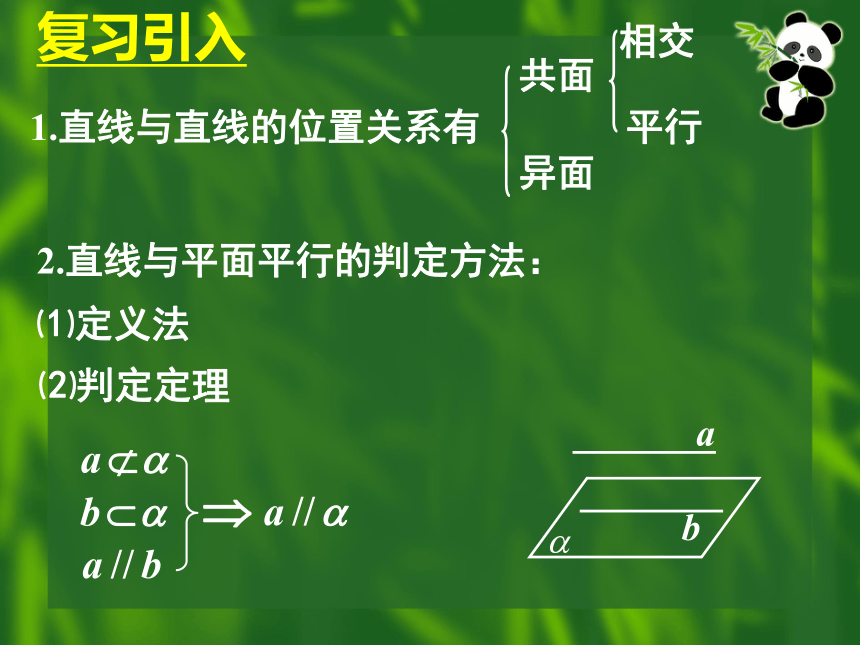
2.直线与平面平行的判定方法:
复习引入
2.直线与平面平行的判定方法:
⑴定义法
1.直线与直线的位置关系有
共面
异面
平行
相交
复习引入
2.直线与平面平行的判定方法:
⑴定义法
⑵判定定理
1.直线与直线的位置关系有
共面
异面
平行
相交
复习引入
2.直线与平面平行的判定方法:
⑴定义法
⑵判定定理
a
b
1.直线与直线的位置关系有
共面
异面
平行
相交
复习引入
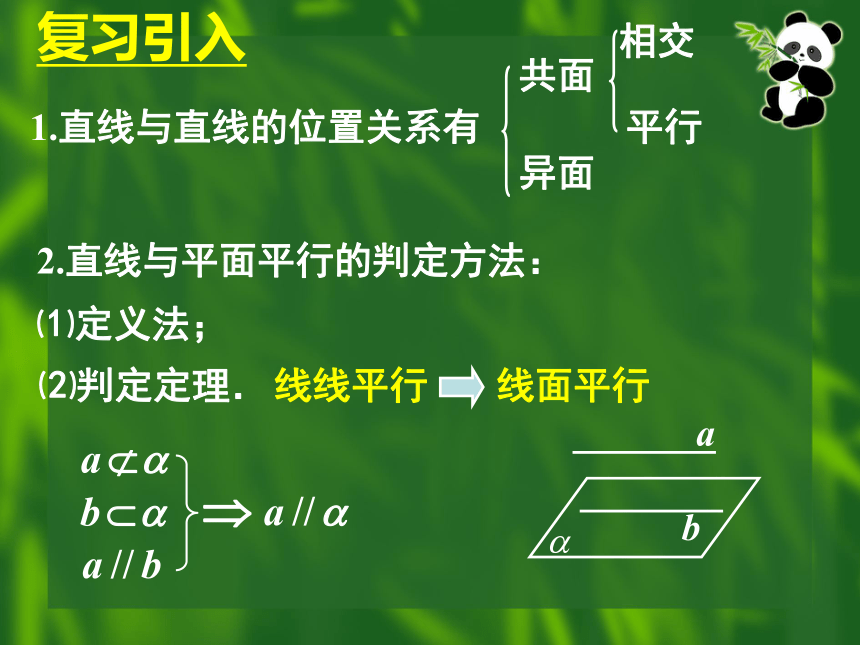
2.直线与平面平行的判定方法:
⑴定义法;
⑵判定定理.
线线平行
线面平行
a
b
1.直线与直线的位置关系有
共面
异面
平行
相交
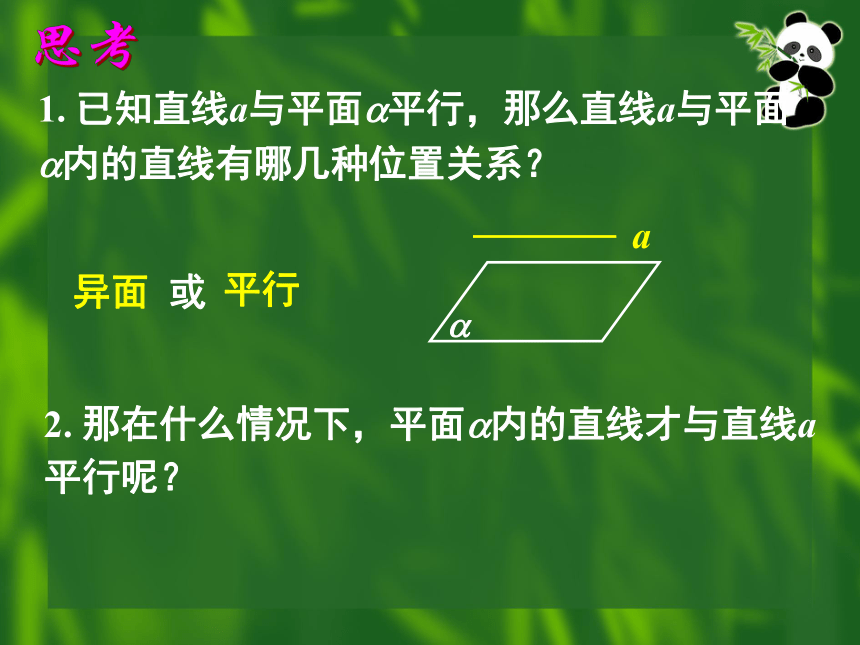
1. 已知直线a与平面 平行,那么直线a与平面
内的直线有哪几种位置关系?
a
1. 已知直线a与平面 平行,那么直线a与平面
内的直线有哪几种位置关系?
异面 或
平行
a
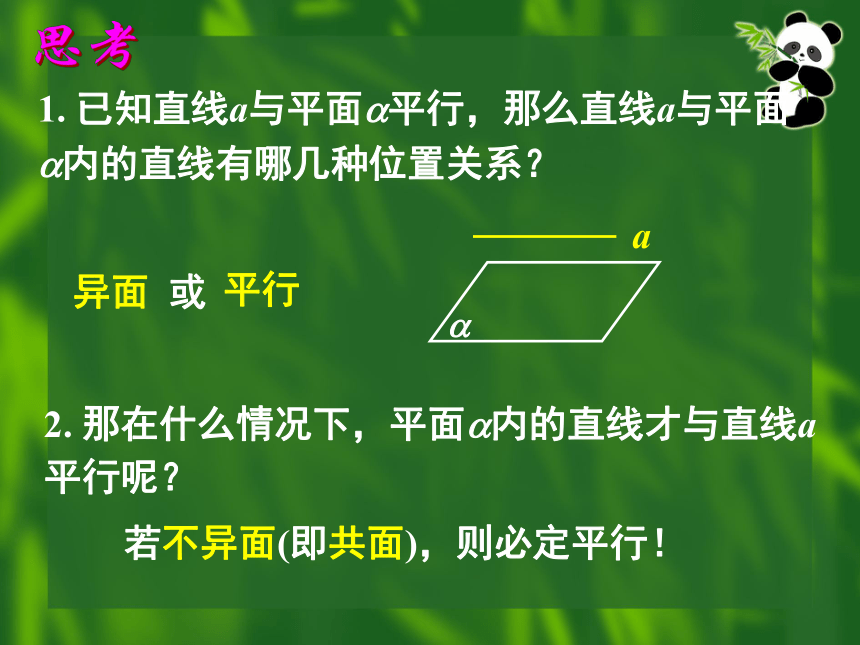
1. 已知直线a与平面 平行,那么直线a与平面
内的直线有哪几种位置关系?
异面 或
平行
2. 那在什么情况下,平面 内的直线才与直线a平行呢?
a
1. 已知直线a与平面 平行,那么直线a与平面
内的直线有哪几种位置关系?
异面 或
平行
若不异面(即共面),则必定平行!
a
2. 那在什么情况下,平面 内的直线才与直线a平行呢?
a
已知:直线a∥平面 ,
a
已知:直线a∥平面 ,
a
a
b
已知:直线a∥平面 ,
求证:a∥b.
a
b
已知:直线a∥平面 ,
证明:
求证:a∥b.
a
b
已知:直线a∥平面 ,
证明:
求证:a∥b.
a
b
已知:直线a∥平面 ,
证明:
∴a与b无公共点
求证:a∥b.
a
b
已知:直线a∥平面 ,
证明:
∴a与b无公共点
求证:a∥b.
又∵
a
b
已知:直线a∥平面 ,
证明:
∴a与b无公共点
求证:a∥b.
又∵
即a与b共面.
a
b
已知:直线a∥平面 ,
证明:
∴a与b无公共点
求证:a∥b.
又∵
即a与b共面.
∴ a∥b.
a
b
已知:直线a∥平面 ,
讲授新课
直线与平面平行的性质定理:
a
b
讲授新课
直线与平面平行的性质定理:
一条直线与一个平面平行,则过这条直线的任一个平面与此平面的交线和该直线平行.
a
b
讲授新课
直线与平面平行的性质定理
一条直线与一个平面平行,则过这条直线的任一个平面与此平面的交线和该直线平行.
符号语言:
a
b
讲授新课
直线与平面平行的性质定理
一条直线与一个平面平行,则过这条直线的任一个平面与此平面的交线和该直线平行.
a∥b.
符号语言:
a
b
讲授新课
直线与平面平行的性质定理
一条直线与一个平面平行,则过这条直线的任一个平面与此平面的交线和该直线平行.
线面平行
线线平行
a∥b.
符号语言:
a
b
例1 如图,一块木料中,棱BC平行于面A'C'.
P
B
C
A
D
A'
B'
C'
D'
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
例1 如图,一块木料中,棱BC平行于面A'C'.
作直线EF//B'C',
棱A'B'、C'D'于点E、F,
解:
⑴如图,
在平面A'C'内,
分别交
F
P
B
C
A
D
A'
B'
C'
D'
E
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
例1 如图,一块木料中,棱BC平行于面A'C'.
作直线EF//B'C',
棱A'B'、C'D'于点E、F,
连结BE、CF,
F
P
B
C
A
D
A'
B'
C'
D'
E
解:
⑴如图,
在平面A'C'内,
分别交
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
例1 如图,一块木料中,棱BC平行于面A'C'.
作直线EF//B'C',
棱A'B'、C'D'于点E、F,
连结BE、CF,
F
P
B
C
A
D
A'
B'
C'
D'
E
解:
⑴如图,
在平面A'C'内,
下面证明EF、BE、
CF为应画的线.
分别交
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑴
例1 如图,一块木料中,棱BC平行于面A'C'.
解:
F
P
B
C
A
D
A'
B'
C'
D'
E
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑴
例1 如图,一块木料中,棱BC平行于面A'C'.
解:
F
P
B
C
A
D
A'
B'
C'
D'
E
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑴
BC//B'C'
例1 如图,一块木料中,棱BC平行于面A'C'.
解:
F
P
B
C
A
D
A'
B'
C'
D'
E
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑴
BC//B'C'
EF//B'C'
BC//EF
例1 如图,一块木料中,棱BC平行于面A'C'.
解:
F
P
B
C
A
D
A'
B'
C'
D'
E
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑴
BC//B'C'
EF//B'C'
BC//EF
EF、BE、CF共面.
例1 如图,一块木料中,棱BC平行于面A'C'.
解:
F
P
B
C
A
D
A'
B'
C'
D'
E
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑴
则EF、BE、CF为应画的线.
BC//B'C'
EF//B'C'
BC//EF
EF、BE、CF共面.
例1 如图,一块木料中,棱BC平行于面A'C'.
解:
F
P
B
C
A
D
A'
B'
C'
D'
E
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
例1 如图,一块木料中,棱BC平行于面A'C'.
F
P
B
C
A
D
A'
B'
C'
D'
E
⑵
解:
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑵所画的线与平面AC是什么位置关系?
例1 如图,一块木料中,棱BC平行于面A'C'.
F
P
B
C
A
D
A'
B'
C'
D'
E
⑵
解:
由⑴,得
EF//BC,
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑵所画的线与平面AC是什么位置关系?
例1 如图,一块木料中,棱BC平行于面A'C'.
F
P
B
C
A
D
A'
B'
C'
D'
E
⑵
解:
由⑴,得
EF//BC,
EF//BC
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑵所画的线与平面AC是什么位置关系?
例1 如图,一块木料中,棱BC平行于面A'C'.
F
P
B
C
A
D
A'
B'
C'
D'
E
⑵
解:
EF//面AC
由⑴,得
EF//BC,
EF//BC
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑵所画的线与平面AC是什么位置关系?
例1 如图,一块木料中,棱BC平行于面A'C'.
F
P
B
C
A
D
A'
B'
C'
D'
E
⑵
解:
EF//面AC
由⑴,得
BE、CF都与平面AC相交.
EF//BC,
EF//BC
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑵所画的线与平面AC是什么位置关系?
例1 如图,一块木料中,棱BC平行于面A'C'.
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑵所画的线与平面AC是什么位置关系?
F
P
B
C
A
D
A'
B'
C'
D'
E
⑵
解:
EF//面AC
由⑴,得
BE、CF都与面相交.
EF//BC,
EF//BC
线面平行
线线平行
线面平行
⑷若平面外的两条平行直线中的一条平行于这
( )
( )
判断下列命题是否正确?
⑴若直线a与平面 平行,则a与 内任何直线平
行.
⑵若直线a、b都和平面 平行,
( )
则a与b平行.
⑶若直线a和平面 , 都平行,
则
练习1:
( )
个平面,则另一条也平行于这个平面.
⑷若平面外的两条平行直线中的一条平行于这
( )
( )
判断下列命题是否正确?
⑴若直线a与平面 平行,则a与 内任何直线平
行.
⑵若直线a、b都和平面 平行,
( )
则a与b平行.
⑶若直线a和平面 , 都平行,
则
练习1:
( )
个平面,则另一条也平行于这个平面.
⑷若平面外的两条平行直线中的一条平行于这
( )
( )
判断下列命题是否正确?
⑴若直线a与平面 平行,则a与 内任何直线平
行.
⑵若直线a、b都和平面 平行,
( )
则a与b平行.
⑶若直线a和平面 , 都平行,
则
练习1:
( )
个平面,则另一条也平行于这个平面.
⑷若平面外的两条平行直线中的一条平行于这
( )
( )
判断下列命题是否正确?
⑴若直线a与平面 平行,则a与 内任何直线平
行.
⑵若直线a、b都和平面 平行,
( )
则a与b平行.
⑶若直线a和平面 , 都平行,
则
练习1:
( )
个平面,则另一条也平行于这个平面.
⑷若平面外的两条平行直线中的一条平行于这
( )
( )
判断下列命题是否正确?
⑴若直线a与平面 平行,则a与 内任何直线平
行.
⑵若直线a、b都和平面 平行,
( )
则a与b平行.
⑶若直线a和平面 , 都平行,
则
练习1:
( )
个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
a
b
且a//b,
已知:直线a、b,平面 ,
b// .
求证:
a
b
证明:
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
a
b
过a作平面 ,
证明:
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
a
b
证明:
且
过a作平面 ,
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
a
b
证明:
且
过a作平面 ,
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
a
b
证明:
且
过a作平面 ,
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
性质定理
a
b
证明:
且
过a作平面 ,
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
性质定理
a
b
证明:
且
过a作平面 ,
a//b
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
性质定理
a
b
证明:
b//c
且
过a作平面 ,
a//b
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
性质定理
a
b
证明:
a//b
b//c
且
过a作平面 ,
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
性质定理
a
b
证明:
b//c
且
过a作平面 ,
a//b
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
性质定理
a
b
证明:
b//c
判定定理
且
过a作平面 ,
a//b
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
练习2:已知正方体ABCD—A1B1C1D1的棱长为
1,点P是面AA1D1D的中心,点Q是B1D1上一
点,
A
B
C
D
A1
B1
C1
D1
P
Q
且PQ//面AB1,则线段 PQ长为 .
练习2:已知正方体ABCD—A1B1C1D1的棱长为1,
点P是面AA1D1D的中心,点Q是B1D1上一点,
解析:
A
B
C
D
A1
B1
C1
D1
P
Q
连结AB1、AD1,
且PQ//面AB1,则线段 PQ长为 .
练习2:已知正方体ABCD—A1B1C1D1的棱长为1,
点P是面AA1D1D的中心,点Q是B1D1上一点,
解析:
A
B
C
D
A1
B1
C1
D1
P
Q
连结AB1、AD1,
∵点P是面AA1D1D的中心,
∴点P是 AD1的中点,
且PQ//面AB1,则线段 PQ长为 .
练习2:已知正方体ABCD—A1B1C1D1的棱长为1,
点P是面AA1D1D的中心,点Q是B1D1上一点,
解析:
A
B
C
D
A1
B1
C1
D1
P
Q
连结AB1、AD1,
∵点P是面AA1D1D的中心,
∴点P是 AD1的中点,
∵PQ//面AB1,
且PQ//面AB1,则线段 PQ长为 .
练习2:已知正方体ABCD—A1B1C1D1的棱长为1,
点P是面AA1D1D的中心,点Q是B1D1上一点,
解析:
A
B
C
D
A1
B1
C1
D1
P
Q
连结AB1、AD1,
∵点P是面AA1D1D的中心,
∴点P是 AD1的中点,
∵PQ//面AB1,
∴PQ//AB1,
且PQ//面AB1,则线段 PQ长为 .
课堂小结
⑴判定定理.
线线平行
线面平行
⑵性质定理.
线面平行
线线平行
1.直线与平面平行的性质定理
2.判定定理与性质定理展示的数学思想方法:
a∥b.
a
b
性质定理的运用:
作业:
习题 2.2A组5
2.2A组6
2.2.3直线与平面
平行的性质
复习引入
1.直线与直线的位置关系有哪几种?
复习引入
1.直线与直线的位置关系有
共面
异面
平行
相交
复习引入
1.直线与直线的位置关系有
共面
异面
平行
相交
2.直线与平面平行的判定方法:
复习引入
2.直线与平面平行的判定方法:
⑴定义法
1.直线与直线的位置关系有
共面
异面
平行
相交
复习引入
2.直线与平面平行的判定方法:
⑴定义法
⑵判定定理
1.直线与直线的位置关系有
共面
异面
平行
相交
复习引入
2.直线与平面平行的判定方法:
⑴定义法
⑵判定定理
a
b
1.直线与直线的位置关系有
共面
异面
平行
相交
复习引入
2.直线与平面平行的判定方法:
⑴定义法;
⑵判定定理.
线线平行
线面平行
a
b
1.直线与直线的位置关系有
共面
异面
平行
相交
1. 已知直线a与平面 平行,那么直线a与平面
内的直线有哪几种位置关系?
a
1. 已知直线a与平面 平行,那么直线a与平面
内的直线有哪几种位置关系?
异面 或
平行
a
1. 已知直线a与平面 平行,那么直线a与平面
内的直线有哪几种位置关系?
异面 或
平行
2. 那在什么情况下,平面 内的直线才与直线a平行呢?
a
1. 已知直线a与平面 平行,那么直线a与平面
内的直线有哪几种位置关系?
异面 或
平行
若不异面(即共面),则必定平行!
a
2. 那在什么情况下,平面 内的直线才与直线a平行呢?
a
已知:直线a∥平面 ,
a
已知:直线a∥平面 ,
a
a
b
已知:直线a∥平面 ,
求证:a∥b.
a
b
已知:直线a∥平面 ,
证明:
求证:a∥b.
a
b
已知:直线a∥平面 ,
证明:
求证:a∥b.
a
b
已知:直线a∥平面 ,
证明:
∴a与b无公共点
求证:a∥b.
a
b
已知:直线a∥平面 ,
证明:
∴a与b无公共点
求证:a∥b.
又∵
a
b
已知:直线a∥平面 ,
证明:
∴a与b无公共点
求证:a∥b.
又∵
即a与b共面.
a
b
已知:直线a∥平面 ,
证明:
∴a与b无公共点
求证:a∥b.
又∵
即a与b共面.
∴ a∥b.
a
b
已知:直线a∥平面 ,
讲授新课
直线与平面平行的性质定理:
a
b
讲授新课
直线与平面平行的性质定理:
一条直线与一个平面平行,则过这条直线的任一个平面与此平面的交线和该直线平行.
a
b
讲授新课
直线与平面平行的性质定理
一条直线与一个平面平行,则过这条直线的任一个平面与此平面的交线和该直线平行.
符号语言:
a
b
讲授新课
直线与平面平行的性质定理
一条直线与一个平面平行,则过这条直线的任一个平面与此平面的交线和该直线平行.
a∥b.
符号语言:
a
b
讲授新课
直线与平面平行的性质定理
一条直线与一个平面平行,则过这条直线的任一个平面与此平面的交线和该直线平行.
线面平行
线线平行
a∥b.
符号语言:
a
b
例1 如图,一块木料中,棱BC平行于面A'C'.
P
B
C
A
D
A'
B'
C'
D'
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
例1 如图,一块木料中,棱BC平行于面A'C'.
作直线EF//B'C',
棱A'B'、C'D'于点E、F,
解:
⑴如图,
在平面A'C'内,
分别交
F
P
B
C
A
D
A'
B'
C'
D'
E
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
例1 如图,一块木料中,棱BC平行于面A'C'.
作直线EF//B'C',
棱A'B'、C'D'于点E、F,
连结BE、CF,
F
P
B
C
A
D
A'
B'
C'
D'
E
解:
⑴如图,
在平面A'C'内,
分别交
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
例1 如图,一块木料中,棱BC平行于面A'C'.
作直线EF//B'C',
棱A'B'、C'D'于点E、F,
连结BE、CF,
F
P
B
C
A
D
A'
B'
C'
D'
E
解:
⑴如图,
在平面A'C'内,
下面证明EF、BE、
CF为应画的线.
分别交
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑴
例1 如图,一块木料中,棱BC平行于面A'C'.
解:
F
P
B
C
A
D
A'
B'
C'
D'
E
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑴
例1 如图,一块木料中,棱BC平行于面A'C'.
解:
F
P
B
C
A
D
A'
B'
C'
D'
E
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑴
BC//B'C'
例1 如图,一块木料中,棱BC平行于面A'C'.
解:
F
P
B
C
A
D
A'
B'
C'
D'
E
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑴
BC//B'C'
EF//B'C'
BC//EF
例1 如图,一块木料中,棱BC平行于面A'C'.
解:
F
P
B
C
A
D
A'
B'
C'
D'
E
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑴
BC//B'C'
EF//B'C'
BC//EF
EF、BE、CF共面.
例1 如图,一块木料中,棱BC平行于面A'C'.
解:
F
P
B
C
A
D
A'
B'
C'
D'
E
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑴
则EF、BE、CF为应画的线.
BC//B'C'
EF//B'C'
BC//EF
EF、BE、CF共面.
例1 如图,一块木料中,棱BC平行于面A'C'.
解:
F
P
B
C
A
D
A'
B'
C'
D'
E
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
例1 如图,一块木料中,棱BC平行于面A'C'.
F
P
B
C
A
D
A'
B'
C'
D'
E
⑵
解:
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑵所画的线与平面AC是什么位置关系?
例1 如图,一块木料中,棱BC平行于面A'C'.
F
P
B
C
A
D
A'
B'
C'
D'
E
⑵
解:
由⑴,得
EF//BC,
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑵所画的线与平面AC是什么位置关系?
例1 如图,一块木料中,棱BC平行于面A'C'.
F
P
B
C
A
D
A'
B'
C'
D'
E
⑵
解:
由⑴,得
EF//BC,
EF//BC
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑵所画的线与平面AC是什么位置关系?
例1 如图,一块木料中,棱BC平行于面A'C'.
F
P
B
C
A
D
A'
B'
C'
D'
E
⑵
解:
EF//面AC
由⑴,得
EF//BC,
EF//BC
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑵所画的线与平面AC是什么位置关系?
例1 如图,一块木料中,棱BC平行于面A'C'.
F
P
B
C
A
D
A'
B'
C'
D'
E
⑵
解:
EF//面AC
由⑴,得
BE、CF都与平面AC相交.
EF//BC,
EF//BC
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑵所画的线与平面AC是什么位置关系?
例1 如图,一块木料中,棱BC平行于面A'C'.
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑵所画的线与平面AC是什么位置关系?
F
P
B
C
A
D
A'
B'
C'
D'
E
⑵
解:
EF//面AC
由⑴,得
BE、CF都与面相交.
EF//BC,
EF//BC
线面平行
线线平行
线面平行
⑷若平面外的两条平行直线中的一条平行于这
( )
( )
判断下列命题是否正确?
⑴若直线a与平面 平行,则a与 内任何直线平
行.
⑵若直线a、b都和平面 平行,
( )
则a与b平行.
⑶若直线a和平面 , 都平行,
则
练习1:
( )
个平面,则另一条也平行于这个平面.
⑷若平面外的两条平行直线中的一条平行于这
( )
( )
判断下列命题是否正确?
⑴若直线a与平面 平行,则a与 内任何直线平
行.
⑵若直线a、b都和平面 平行,
( )
则a与b平行.
⑶若直线a和平面 , 都平行,
则
练习1:
( )
个平面,则另一条也平行于这个平面.
⑷若平面外的两条平行直线中的一条平行于这
( )
( )
判断下列命题是否正确?
⑴若直线a与平面 平行,则a与 内任何直线平
行.
⑵若直线a、b都和平面 平行,
( )
则a与b平行.
⑶若直线a和平面 , 都平行,
则
练习1:
( )
个平面,则另一条也平行于这个平面.
⑷若平面外的两条平行直线中的一条平行于这
( )
( )
判断下列命题是否正确?
⑴若直线a与平面 平行,则a与 内任何直线平
行.
⑵若直线a、b都和平面 平行,
( )
则a与b平行.
⑶若直线a和平面 , 都平行,
则
练习1:
( )
个平面,则另一条也平行于这个平面.
⑷若平面外的两条平行直线中的一条平行于这
( )
( )
判断下列命题是否正确?
⑴若直线a与平面 平行,则a与 内任何直线平
行.
⑵若直线a、b都和平面 平行,
( )
则a与b平行.
⑶若直线a和平面 , 都平行,
则
练习1:
( )
个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
a
b
且a//b,
已知:直线a、b,平面 ,
b// .
求证:
a
b
证明:
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
a
b
过a作平面 ,
证明:
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
a
b
证明:
且
过a作平面 ,
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
a
b
证明:
且
过a作平面 ,
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
a
b
证明:
且
过a作平面 ,
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
性质定理
a
b
证明:
且
过a作平面 ,
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
性质定理
a
b
证明:
且
过a作平面 ,
a//b
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
性质定理
a
b
证明:
b//c
且
过a作平面 ,
a//b
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
性质定理
a
b
证明:
a//b
b//c
且
过a作平面 ,
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
性质定理
a
b
证明:
b//c
且
过a作平面 ,
a//b
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
已知:直线a、b,平面 ,
b// .
求证:
性质定理
a
b
证明:
b//c
判定定理
且
过a作平面 ,
a//b
c
且a//b,
例2 若平面外的两条平行直线中的一条平行
于这个平面,则另一条也平行于这个平面.
练习2:已知正方体ABCD—A1B1C1D1的棱长为
1,点P是面AA1D1D的中心,点Q是B1D1上一
点,
A
B
C
D
A1
B1
C1
D1
P
Q
且PQ//面AB1,则线段 PQ长为 .
练习2:已知正方体ABCD—A1B1C1D1的棱长为1,
点P是面AA1D1D的中心,点Q是B1D1上一点,
解析:
A
B
C
D
A1
B1
C1
D1
P
Q
连结AB1、AD1,
且PQ//面AB1,则线段 PQ长为 .
练习2:已知正方体ABCD—A1B1C1D1的棱长为1,
点P是面AA1D1D的中心,点Q是B1D1上一点,
解析:
A
B
C
D
A1
B1
C1
D1
P
Q
连结AB1、AD1,
∵点P是面AA1D1D的中心,
∴点P是 AD1的中点,
且PQ//面AB1,则线段 PQ长为 .
练习2:已知正方体ABCD—A1B1C1D1的棱长为1,
点P是面AA1D1D的中心,点Q是B1D1上一点,
解析:
A
B
C
D
A1
B1
C1
D1
P
Q
连结AB1、AD1,
∵点P是面AA1D1D的中心,
∴点P是 AD1的中点,
∵PQ//面AB1,
且PQ//面AB1,则线段 PQ长为 .
练习2:已知正方体ABCD—A1B1C1D1的棱长为1,
点P是面AA1D1D的中心,点Q是B1D1上一点,
解析:
A
B
C
D
A1
B1
C1
D1
P
Q
连结AB1、AD1,
∵点P是面AA1D1D的中心,
∴点P是 AD1的中点,
∵PQ//面AB1,
∴PQ//AB1,
且PQ//面AB1,则线段 PQ长为 .
课堂小结
⑴判定定理.
线线平行
线面平行
⑵性质定理.
线面平行
线线平行
1.直线与平面平行的性质定理
2.判定定理与性质定理展示的数学思想方法:
a∥b.
a
b
性质定理的运用:
作业:
习题 2.2A组5
2.2A组6
