2021-2022学年人教版数学 九年级上册22.1.3 二次函数y=a(x-h)2+ k的图象和性质课件(共44张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学 九年级上册22.1.3 二次函数y=a(x-h)2+ k的图象和性质课件(共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 14:05:32 | ||
图片预览




文档简介
(共44张PPT)
人教版数学 九年级上册
第二十二章 二次函数
22.1.3 二次函数y=a(x-h) +k的图象和性质
第3课时 二次函数y=a(x-h) +k的图象和性质
y=ax2
y=a(x-h)2
y=ax2+k
y=ax2
k>0
k<0
上移
下移
左加
右减
说出平移方式,并指出其顶点与对称轴.
顶点
在x轴上(h,0)
顶点
在y轴上(0,k)
对称轴
y轴
对称轴 x=h
【思考】 顶点不在坐标轴上的二次函数又如何呢?
导入新知
1. 能画出y=a(x-h)2+k (a ≠0)的图象.
2. 理解二次函数y=a(x-h)2+k (a ≠0)与y=ax2 (a ≠0)之间的联系.
3. 能说出抛物线y=a(x-h)2+k的开口方向、对称轴、顶点.
学习目标
画出函数 的图象,并指出它的开口方向、
对称轴和顶点.
解:
-4
-2
y
-6
O
-2
2
x
4
-4
开口方向:
对称轴:
顶点:
向下.
x=-1.
(-1,-1).
新知一 二次函数y=a(x-h)2+k的图象和性质
合作探究
-4
-2
y
-6
O
-2
2
x
4
-4
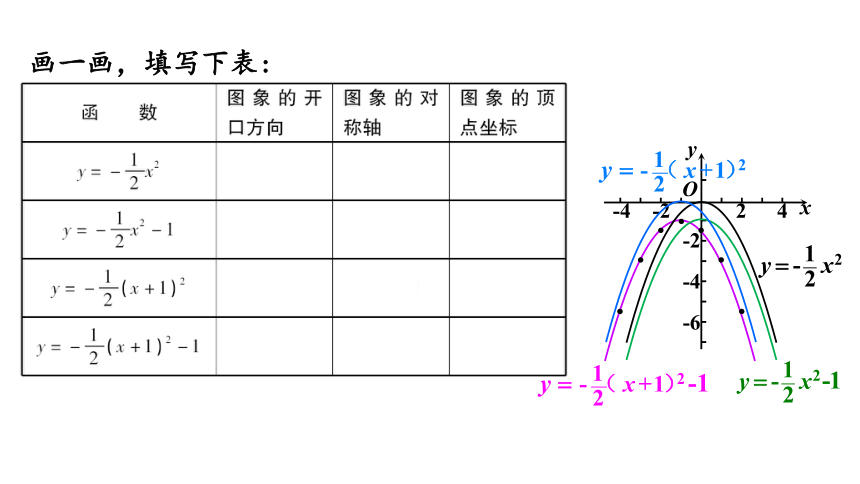
画一画,填写下表:
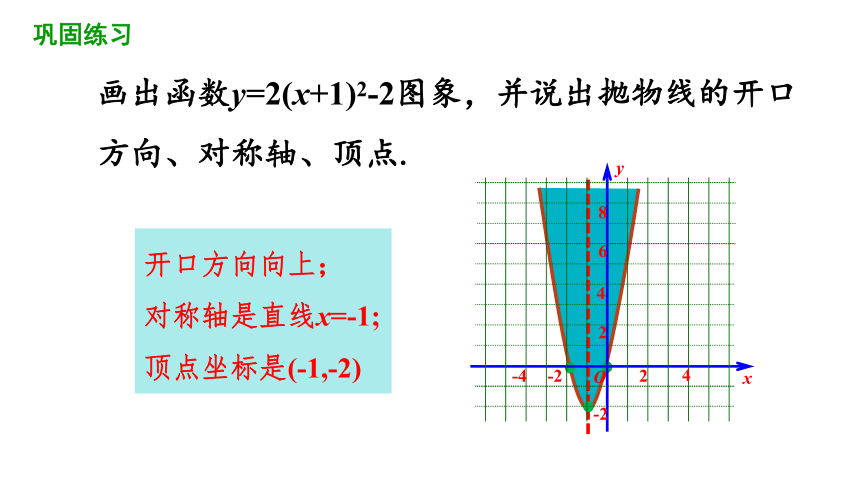
画出函数y=2(x+1)2-2图象,并说出抛物线的开口方向、对称轴、顶点.
开口方向向上;
对称轴是直线x=-1;
顶点坐标是(-1,-2)
-2
2
x
y
O
-2
4
6
8
-4
2
4
巩固练习
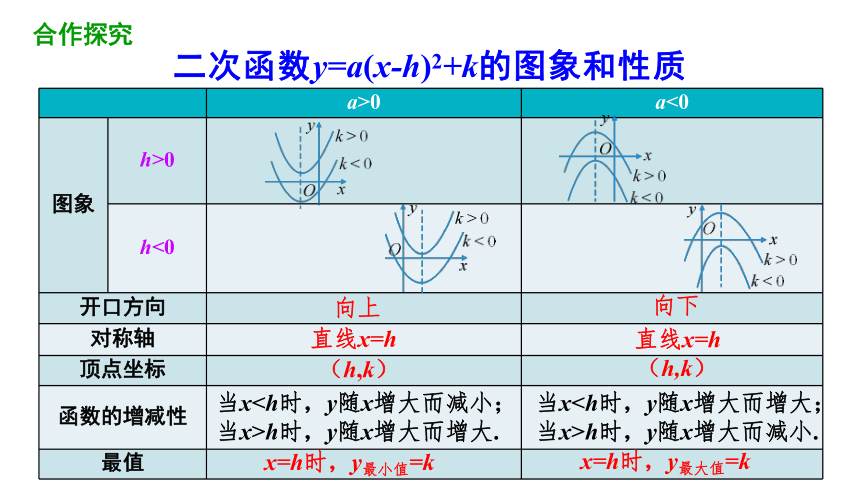
a>0 a<0
图象 h>0
h<0
开口方向
对称轴
顶点坐标
函数的增减性
最值
当xh时,y随x增大而减小.
当xh时,y随x增大而增大.
向上
向下
直线x=h
直线x=h
(h,k)
x=h时,y最小值=k
x=h时,y最大值=k
(h,k)
二次函数y=a(x-h)2+k的图象和性质
合作探究
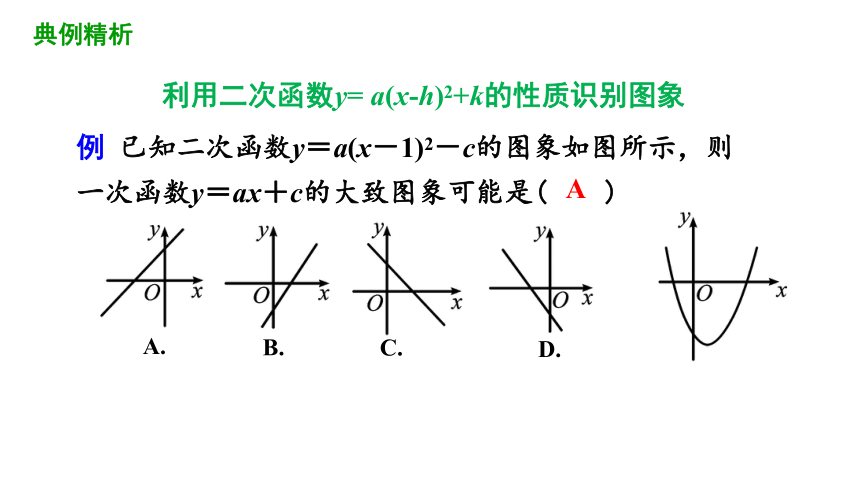
例 已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象可能是( )
A
利用二次函数y= a(x-h)2+k的性质识别图象
B.
D.
A.
C.
典例精析
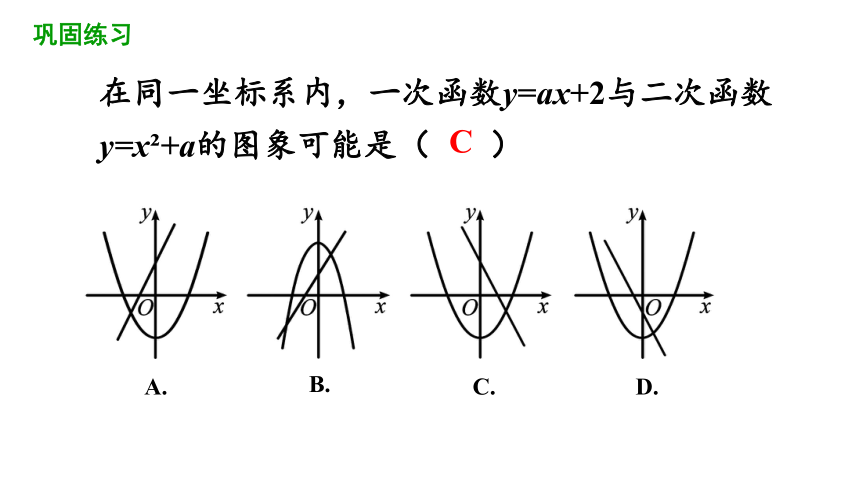
在同一坐标系内,一次函数y=ax+2与二次函数y=x +a的图象可能是( )
C
A.
B.
D.
C.
巩固练习
-4
-2
y
-6
O
-2
2
x
4
-4
向左平移一个单位
向下平移一个单位
向左平移一个单位,
再向下平移一个单位
新知二 二次函数y= a(x-h)2+k的图象与平移
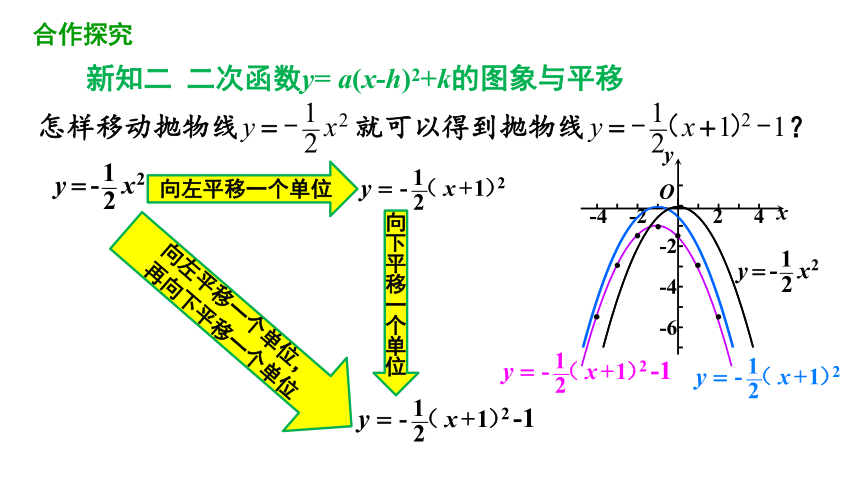
怎样移动抛物线 就可以得到抛物线 ?
合作探究
向左平移
1个单位
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
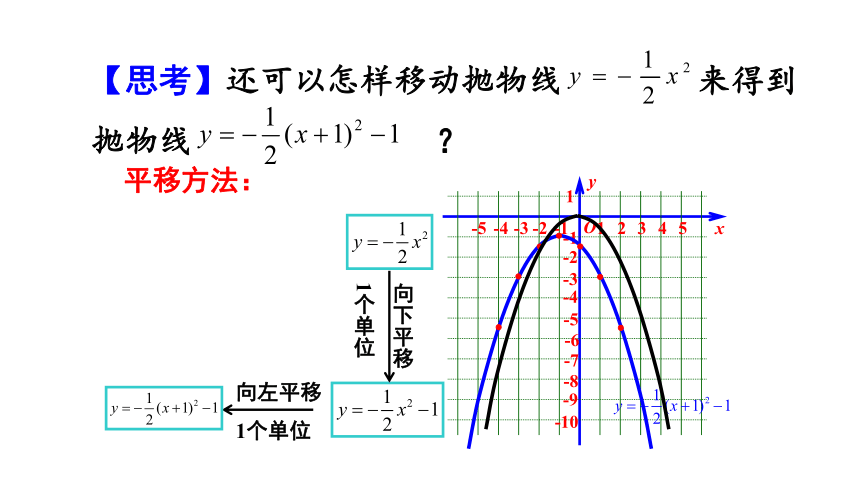
【思考】还可以怎样移动抛物线 来得到抛物线 ?
平移方法:
向下平移
1个单位
y=a(x-h)2+k
y=ax2
平移关系
?
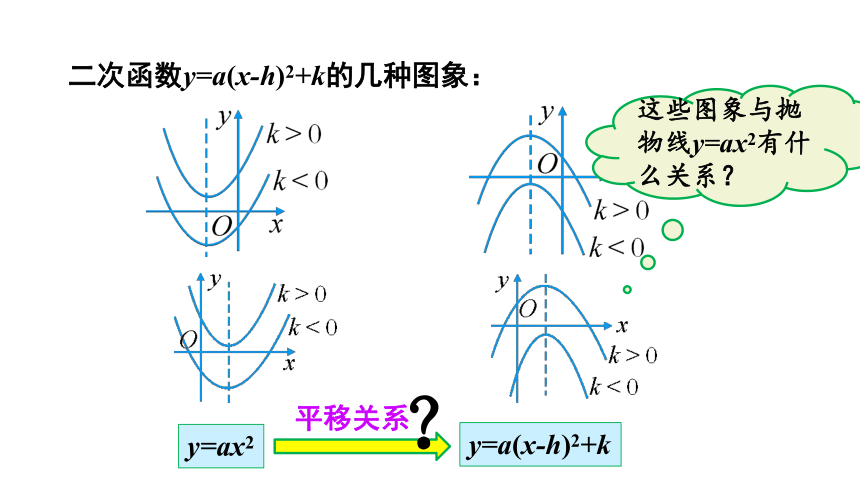
二次函数y=a(x-h)2+k的几种图象:
这些图象与抛物线y=ax2有什么关系?
一般地,抛物线y=a(x-h) +k与y=ax 形状相同,位置不同.把抛物线y=ax 向上(下)向右(左)平移,可以得到抛物线y=a(x-h) +k.平移的方向、距离要根据h、k的值来决定.
向左(右)平移|h|个单位
向上(下)平移|k|个单位
y=ax2
y=a(x-h)2
y=a(x-h) 2+k
y=ax2
y=a(x-h)2+k
向上(下)平移|k|个单位
y=ax +k
向左(右)平移|h|个单位
平移方法:
方法点拨
(1)当a>0时, 开口向上;
当a<0时,开口向下;
(2)对称轴是直线x=h;
(3)顶点是(h,k).
抛物线y=a(x-h)2+k的特点
可以看作互相平移得到的.
y = ax2
y = ax2 + k
y = a(x - h )2
y = a( x - h )2 + k
上下平移
左右平移
上下平移
左右平移
平移规律
简记为:
上下平移,
括号外上加下减;
左右平移,
括号内左加右减.
二次项系数a不变.
二次函数y=ax2 与y=a(x-h)2+k的关系
合作探究
如果一条抛物线的形状与 形状相同,且顶点坐标是(4,2),试求这个函数关系式.
巩固练习
例 要修建一个圆形喷水池,在池中心竖直安装一根水管.在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长
二次函数的应用
典例精析
C(3,0)
B(1,3)
A
x
O
y
1
2
3
1
2
3
解:如图建立直角坐标系,
点(1,3)是图中这段抛物线的顶点.
因此可设这段抛物线对应的函数是
∵这段抛物线经过点(3,0),
∴ 0=a(3-1)2+3.
解得:
因此抛物线的解析式为:
y=a(x-1)2+3 (0≤x≤3).
当x=0时,y=2.25.
答:水管长应为2.25m.
3
4
a=- .
y= (x-1)2+3 (0≤x≤3).
3
4
-
如图所示,已知一个大门呈抛物线型,其地面宽度AB=18m,一个同学站在门内,在离门脚B点1m远的D处,垂直地面立起一根1.7m长的木杆,其顶端恰好定在抛物线形门上C处,请你求出大门的高h的值.
巩固练习
解:如图,建立平面直角坐标系,
设抛物线解析式为y=ax2+k.由题意得B(9, 0),C(8, 1.7).
把B、C两点的坐标代入y=ax2+k,得
解得
∴y=-0.1x2+8.1,∴h=k=8.1,即大门高8.1m.
二次函数 开口方向 对称轴 顶点坐标
y=2(x+3)2+5
向上
( 1, -2 )
向下
向下
( 3 , 7)
( 2 , -6 )
向上
直线x=-3
直线x=1
直线x=3
直线x=2
(-3, 5 )
y=-3(x-1)2-2
y = 4(x-3)2+7
y=-5(2-x)2-6
1.完成下表:
课堂练习
2.把抛物线y=-3x2先向上平移2个单位,再向右平移1个单位,那么所得抛物线是___________________.
4.抛物线y=-3(x-1)2+2的图象如何得到 y=-3x2 .
3.抛物线y=-3x2+2的图象向右平移2个单位,再向上平移1个单位,得到抛物线的解析式为 _____________ .
答:先向左平移一个单位,再向下平移两个单位.
5.已知一个二次函数图象的顶点为A(-1,3),且它是由二次函数y=5x2平移得到,请直接写出该二次函数的解析式.
设该二次函数的解析式为y=a(x-h)2+k,
由题意得y=5(x+1)2+3.
向右(h>0)[或向左(h<0)]平移|h|个单位
y=ax2
y=a(x-h)2
y=a(x-h)2+k
y=ax2+k
向上(k>0)[或向下(k<0)]平移|k|个单位
向右(h>0)[或向左(h<0)]平移|h|个单位
向上(k>0)[或向下(k<0)]平移|k|个单位
向右(h>0)[或向左(h<0)]平移|h|个单位
向上(k>0)[或向下(k<0)]平移|k|个单位
y
O
x
y=ax2
y=a(x-h)2+k
h
k
归纳新知
1.抛物线y=3(x-1)2+1的顶点是( )
A.(1,1)
B.(-1,1)
C.(-1,-1)
D.(1,-1)
A
课后练习
C
3.在函数y=(x+1)2+3中,若y随x的增大而减小,则x的取值范围为( )
A.x>-1 B.x>3
C.x<-1 D.x<3
C
C
5.二次函数y=2(x-3)2-4的最小值为____.
-4
(1)解:开口向上,对称轴是x=1, 顶点(1,2)
(2)解:开口向下,对称轴是x=-1,顶点(-1,-5)
8.已知抛物线y=a(x-3)2+2经过点(1,-2).
(1)求a的值;
(2)若点A(m,y1),B(n,y2)(m<n<3)都在该抛物线上,试比较y1与y2的大小.
解:(1)a=-1
(2)由题意得抛物线的对称轴是直线x=3,∵抛物线开口向下,∴当x<3时,y随x的增大而增大,而m<n<3,∴y1<y2
9.抛物线y=(x+2)2-1可以由抛物线y=x2平移得到,下列平移方法中正确的是( )
A.先向左平移2个单位长度,再向上平移1个单位长度
B.先向左平移2个单位长度,再向下平移1个单位长度
C.先向右平移2个单位长度,再向上平移1个单位长度
D.先向右平移2个单位长度,再向下平移1个单位长度
B
10.将如图所示的抛物线向右平移1个单位长度,再向上平移3个单位长度后,得到的抛物线解析式是( )
A.y=(x-1)2+1
B.y=(x+1)2+1
C.y=2(x-1)2+1
D.y=2(x+1)2+1
C
11.如图,动点A在抛物线y=-(x-1)2+4(0≤x≤3)上运动,直线l经过点(0,6),且与y轴垂直,过点A作AC⊥l于点C,以AC为对角线作矩形ABCD,则另一对角线BD的取值范围正确的是( )
A.2≤BD≤3 B.3≤BD≤6
C.1≤BD≤6 D.2≤BD≤6
D
12.(2020·南京)下列关于二次函数y=-(x-m)2+m2+1(m为常数)的结论:①该函数的图象与函数y=-x2的图象形状相同;②该函数的图象一定经过点(0,1);③当x>0时,y随x的增大而减小;④该函数的图象的顶点在函数y=x2+1的图象上.其中所有正确结论的序号是________.
①②④
16.已知抛物线y=-(x-m)2+1与x轴的交点为A,B(点B在点A的右边),与y轴的交点为C.
(1)写出m=1时与抛物线有关的三个正确结论.
(2)当点B在原点的右边,点C在原点的下方时,是否存在△BOC为等腰三角形的情形?若存在,求出m的值;若不存在,请说明理由.
解:(1)正确的结论有:①顶点坐标为(1,1);②图象开口向下;③图象的对称轴为直线x=1;④函数有最大值1;⑤当x<1时,y随x的增大而增大;⑥当x>1时,y随x的增大而减小等(选答3个即可)
再 见
人教版数学 九年级上册
第二十二章 二次函数
22.1.3 二次函数y=a(x-h) +k的图象和性质
第3课时 二次函数y=a(x-h) +k的图象和性质
y=ax2
y=a(x-h)2
y=ax2+k
y=ax2
k>0
k<0
上移
下移
左加
右减
说出平移方式,并指出其顶点与对称轴.
顶点
在x轴上(h,0)
顶点
在y轴上(0,k)
对称轴
y轴
对称轴 x=h
【思考】 顶点不在坐标轴上的二次函数又如何呢?
导入新知
1. 能画出y=a(x-h)2+k (a ≠0)的图象.
2. 理解二次函数y=a(x-h)2+k (a ≠0)与y=ax2 (a ≠0)之间的联系.
3. 能说出抛物线y=a(x-h)2+k的开口方向、对称轴、顶点.
学习目标
画出函数 的图象,并指出它的开口方向、
对称轴和顶点.
解:
-4
-2
y
-6
O
-2
2
x
4
-4
开口方向:
对称轴:
顶点:
向下.
x=-1.
(-1,-1).
新知一 二次函数y=a(x-h)2+k的图象和性质
合作探究
-4
-2
y
-6
O
-2
2
x
4
-4
画一画,填写下表:
画出函数y=2(x+1)2-2图象,并说出抛物线的开口方向、对称轴、顶点.
开口方向向上;
对称轴是直线x=-1;
顶点坐标是(-1,-2)
-2
2
x
y
O
-2
4
6
8
-4
2
4
巩固练习
a>0 a<0
图象 h>0
h<0
开口方向
对称轴
顶点坐标
函数的增减性
最值
当x
当x
向上
向下
直线x=h
直线x=h
(h,k)
x=h时,y最小值=k
x=h时,y最大值=k
(h,k)
二次函数y=a(x-h)2+k的图象和性质
合作探究
例 已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象可能是( )
A
利用二次函数y= a(x-h)2+k的性质识别图象
B.
D.
A.
C.
典例精析
在同一坐标系内,一次函数y=ax+2与二次函数y=x +a的图象可能是( )
C
A.
B.
D.
C.
巩固练习
-4
-2
y
-6
O
-2
2
x
4
-4
向左平移一个单位
向下平移一个单位
向左平移一个单位,
再向下平移一个单位
新知二 二次函数y= a(x-h)2+k的图象与平移
怎样移动抛物线 就可以得到抛物线 ?
合作探究
向左平移
1个单位
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
【思考】还可以怎样移动抛物线 来得到抛物线 ?
平移方法:
向下平移
1个单位
y=a(x-h)2+k
y=ax2
平移关系
?
二次函数y=a(x-h)2+k的几种图象:
这些图象与抛物线y=ax2有什么关系?
一般地,抛物线y=a(x-h) +k与y=ax 形状相同,位置不同.把抛物线y=ax 向上(下)向右(左)平移,可以得到抛物线y=a(x-h) +k.平移的方向、距离要根据h、k的值来决定.
向左(右)平移|h|个单位
向上(下)平移|k|个单位
y=ax2
y=a(x-h)2
y=a(x-h) 2+k
y=ax2
y=a(x-h)2+k
向上(下)平移|k|个单位
y=ax +k
向左(右)平移|h|个单位
平移方法:
方法点拨
(1)当a>0时, 开口向上;
当a<0时,开口向下;
(2)对称轴是直线x=h;
(3)顶点是(h,k).
抛物线y=a(x-h)2+k的特点
可以看作互相平移得到的.
y = ax2
y = ax2 + k
y = a(x - h )2
y = a( x - h )2 + k
上下平移
左右平移
上下平移
左右平移
平移规律
简记为:
上下平移,
括号外上加下减;
左右平移,
括号内左加右减.
二次项系数a不变.
二次函数y=ax2 与y=a(x-h)2+k的关系
合作探究
如果一条抛物线的形状与 形状相同,且顶点坐标是(4,2),试求这个函数关系式.
巩固练习
例 要修建一个圆形喷水池,在池中心竖直安装一根水管.在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长
二次函数的应用
典例精析
C(3,0)
B(1,3)
A
x
O
y
1
2
3
1
2
3
解:如图建立直角坐标系,
点(1,3)是图中这段抛物线的顶点.
因此可设这段抛物线对应的函数是
∵这段抛物线经过点(3,0),
∴ 0=a(3-1)2+3.
解得:
因此抛物线的解析式为:
y=a(x-1)2+3 (0≤x≤3).
当x=0时,y=2.25.
答:水管长应为2.25m.
3
4
a=- .
y= (x-1)2+3 (0≤x≤3).
3
4
-
如图所示,已知一个大门呈抛物线型,其地面宽度AB=18m,一个同学站在门内,在离门脚B点1m远的D处,垂直地面立起一根1.7m长的木杆,其顶端恰好定在抛物线形门上C处,请你求出大门的高h的值.
巩固练习
解:如图,建立平面直角坐标系,
设抛物线解析式为y=ax2+k.由题意得B(9, 0),C(8, 1.7).
把B、C两点的坐标代入y=ax2+k,得
解得
∴y=-0.1x2+8.1,∴h=k=8.1,即大门高8.1m.
二次函数 开口方向 对称轴 顶点坐标
y=2(x+3)2+5
向上
( 1, -2 )
向下
向下
( 3 , 7)
( 2 , -6 )
向上
直线x=-3
直线x=1
直线x=3
直线x=2
(-3, 5 )
y=-3(x-1)2-2
y = 4(x-3)2+7
y=-5(2-x)2-6
1.完成下表:
课堂练习
2.把抛物线y=-3x2先向上平移2个单位,再向右平移1个单位,那么所得抛物线是___________________.
4.抛物线y=-3(x-1)2+2的图象如何得到 y=-3x2 .
3.抛物线y=-3x2+2的图象向右平移2个单位,再向上平移1个单位,得到抛物线的解析式为 _____________ .
答:先向左平移一个单位,再向下平移两个单位.
5.已知一个二次函数图象的顶点为A(-1,3),且它是由二次函数y=5x2平移得到,请直接写出该二次函数的解析式.
设该二次函数的解析式为y=a(x-h)2+k,
由题意得y=5(x+1)2+3.
向右(h>0)[或向左(h<0)]平移|h|个单位
y=ax2
y=a(x-h)2
y=a(x-h)2+k
y=ax2+k
向上(k>0)[或向下(k<0)]平移|k|个单位
向右(h>0)[或向左(h<0)]平移|h|个单位
向上(k>0)[或向下(k<0)]平移|k|个单位
向右(h>0)[或向左(h<0)]平移|h|个单位
向上(k>0)[或向下(k<0)]平移|k|个单位
y
O
x
y=ax2
y=a(x-h)2+k
h
k
归纳新知
1.抛物线y=3(x-1)2+1的顶点是( )
A.(1,1)
B.(-1,1)
C.(-1,-1)
D.(1,-1)
A
课后练习
C
3.在函数y=(x+1)2+3中,若y随x的增大而减小,则x的取值范围为( )
A.x>-1 B.x>3
C.x<-1 D.x<3
C
C
5.二次函数y=2(x-3)2-4的最小值为____.
-4
(1)解:开口向上,对称轴是x=1, 顶点(1,2)
(2)解:开口向下,对称轴是x=-1,顶点(-1,-5)
8.已知抛物线y=a(x-3)2+2经过点(1,-2).
(1)求a的值;
(2)若点A(m,y1),B(n,y2)(m<n<3)都在该抛物线上,试比较y1与y2的大小.
解:(1)a=-1
(2)由题意得抛物线的对称轴是直线x=3,∵抛物线开口向下,∴当x<3时,y随x的增大而增大,而m<n<3,∴y1<y2
9.抛物线y=(x+2)2-1可以由抛物线y=x2平移得到,下列平移方法中正确的是( )
A.先向左平移2个单位长度,再向上平移1个单位长度
B.先向左平移2个单位长度,再向下平移1个单位长度
C.先向右平移2个单位长度,再向上平移1个单位长度
D.先向右平移2个单位长度,再向下平移1个单位长度
B
10.将如图所示的抛物线向右平移1个单位长度,再向上平移3个单位长度后,得到的抛物线解析式是( )
A.y=(x-1)2+1
B.y=(x+1)2+1
C.y=2(x-1)2+1
D.y=2(x+1)2+1
C
11.如图,动点A在抛物线y=-(x-1)2+4(0≤x≤3)上运动,直线l经过点(0,6),且与y轴垂直,过点A作AC⊥l于点C,以AC为对角线作矩形ABCD,则另一对角线BD的取值范围正确的是( )
A.2≤BD≤3 B.3≤BD≤6
C.1≤BD≤6 D.2≤BD≤6
D
12.(2020·南京)下列关于二次函数y=-(x-m)2+m2+1(m为常数)的结论:①该函数的图象与函数y=-x2的图象形状相同;②该函数的图象一定经过点(0,1);③当x>0时,y随x的增大而减小;④该函数的图象的顶点在函数y=x2+1的图象上.其中所有正确结论的序号是________.
①②④
16.已知抛物线y=-(x-m)2+1与x轴的交点为A,B(点B在点A的右边),与y轴的交点为C.
(1)写出m=1时与抛物线有关的三个正确结论.
(2)当点B在原点的右边,点C在原点的下方时,是否存在△BOC为等腰三角形的情形?若存在,求出m的值;若不存在,请说明理由.
解:(1)正确的结论有:①顶点坐标为(1,1);②图象开口向下;③图象的对称轴为直线x=1;④函数有最大值1;⑤当x<1时,y随x的增大而增大;⑥当x>1时,y随x的增大而减小等(选答3个即可)
再 见
同课章节目录
