2021-2022学年人教版七年级数学上册3.3解一元一次方程(二)(第一课时)课件(共41张PPT)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册3.3解一元一次方程(二)(第一课时)课件(共41张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 728.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 14:14:39 | ||
图片预览











文档简介
(共41张PPT)
第三章 一元一次方程
3.3解一元一次方程(二)
第一课时
【学习目标】
1.了解“去括号”是解方程的重要步骤.
2.准确而熟练地运用去括号法则解带有括号的一元一次方程.
3.进一步培养学生分析解决问题的能力。
【课前预习】
1.在解方程3(x-1)-(x-3)=0 时,去括号正确的是( )
A.3x-1-x+3=0 B.3x-3-x-3=0 C.3x-1-x-3=0 D.3x-3-x+3=0
2.代数式a-2与1-2a的差是0,则a的值是( )
A.1 B.0 C.3 D.2
3.若方程2(2x-3)=1-3x的解与关于x的方程8-m=2(x+1)的解相同,则m的值为( )
A.-4 B.4 C.-12 D.12
4.解方程4.5(x+0.7)=9x,最简便的方法应该首先( )
A.去括号 B.方程两边同时乘以10 C.移项 D.方程两边同时除以4.5
5.当x=4时,式子5(x+m)-10与式子mx+4x的值相等,则m=( )
A.-2; B.2; C.4; D.6;
【课前预习】答案
1.D
2.A
3.B
4.D
5.D
化简下列各式:
(1) (-3a+2b) +3(a-b);
(2) -5a+4b-(-3a+b).
解:(1) 原式=-b;(2) 原式=-2a+3b.
复习回顾
去掉“+ ( )”,括号内各项的符号不变.
去掉“– ( )”,括号内各项的符号改变.
去括号法则:
用三个字母a,b,c表示去括号前后的变化规律:
a + (b + c) =
a -(b + c) =
a + b + c
a -b - c
移项,合并同类项,系数为化1,要注意什么?
②合并同类项时,只是把同类项的系数相加作为所得项的系数,字母部分不变。
③系数化为1,要方程两边同时除以未知数前面的系数。
①移项要变号。
★ 我们在方程6x-7=4x-1上加上一个括号得
6x-7=4(x-1)会解吗?
★ 再在前面再加上一个负号得6x-7=-4(x-1)
会解吗?
讨论
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 kW h (千瓦 时), 全年用电15万kW h. 这个工厂去年上半年每月平均用电是多少?
问 题
一、利用去括号解一元一次方程
设上半年每月平均用电x kW h,则下半年每月平均用电(x- 2 000) kW h; 上半年共用电6x kW h,下半年共用电6(x- 2 000) kW h.根据全年用电15万kW h,列得方程
6x+6(x- 2 000) =150 000.
如果去括号,就能简化方程的形式.
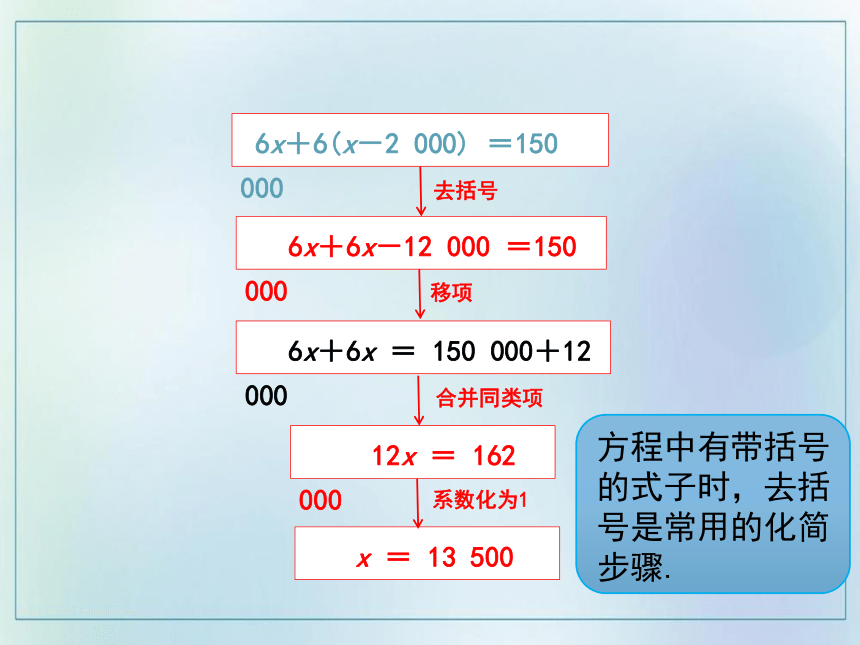
下面的框图表示了解这个方程的流程.
6x+6(x-2 000) =150 000
6x+6x-12 000 =150 000
6x+6x = 150 000+12 000
12x = 162 000
x = 13 500
去括号
移项
合并同类项
系数化为1
方程中有带括号的式子时,去括号是常用的化简步骤.
去括号的目的是能利用移项法解方程;其实质是
乘法的分配律.
例1 解下列方程:
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
典例精析
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
通过以上解方程的过程,你能总结出解含有括号的一元一次方程的一般步骤吗?
去括号
移项
合并同类项
系数化为1
解含有括号的一元一次方程时,要先利用前面学习的去括号法则去掉括号,再利用移项法解方程.
去括号解一元一次方程的步骤:
第一步:去括号(按照去括号法则去括号);
第二步:用移项法解这个一元一次方程:
移项→合并同类项→系数化为1.
移项,合并同类项,系数化为1,要注意什么?
②合并同类项时,只是把同类项的系数相加作为所得项的系数,字母部分不变.
③系数化为1,也就是说方程两边同时除以未知数前面的系数.
①移项时要变号.(变成相反数)
例2 解方程
3x-7(x-1)=3-2(x+3).
解:去括号,得:
3x-7x+7=3-2x -6.
移项得
3x-7x+2x =3-6-7.
合并同类项得
-2x=-10.
系数化为1,得
x=5.
例3 解方程:
导引:初看本例,我们可以利用去括号法解,但 我们只要仔细分析本例的特征,不难发现四个括号里,有两个(x+1)和两个(x-1),因此可先将它们各看作一个整体,再移项、合并进行解答.
解:移项,得
合并,得
去括号,得
移项,得
合并同类项,得-x=-4.
系数化为1,得x=4.
1. 一般行程问题
1. 行程问题中的基本关系式:
路程=速度×时间,
时间=路程÷速度,
速度=路程÷时间.
二、去括号解方程的应用
2. 行程问题中的相等关系:
(1)相遇问题中的相等关系:
①若甲、乙相向而行,甲走的路程+乙走的路程
=甲、乙出发点之间的路程;
②若甲、乙同时出发,甲用的时间=乙用的时间.
(2)追及问题中的相等关系:
①快者走的路程-慢者走的路程=追及路程;
②若同时出发,快者追上慢者时,快者用的时
间=慢者用的时间.
例4 甲站和乙站相距1 500 km,一列慢车从甲站开出,速度为60 km/h,一列快车从乙站开出,速度为90 km/h.
(1)若两车相向而行,慢车先开30 min,快车开出几小时后两车相遇?
(2)若两车同时开出,相背而行,多少小时后两
车相距1 800 km
(3)若两车同时开出,快车在慢车后面同向而行,
多少小时后两车相距1 200 km(此时快车在慢
车的后面)
导引:(1)设快车开出x h后两车相遇.列表:
相等关系:慢车行驶的路程+快车行驶的
路程=1 500 km.
路程/km 速度/(km/h) 时间/h
慢车 60
快车 90x 90 x
(2)设y h后两车相距1 800 km.列表:
相等关系:
两车行驶的路程和+1 500 km=1 800 km.
路程/km 速度/(km/h) 时间/h
慢车 60y 60 y
快车 90y 90 y
(3)设z h后两车相距1 200 km(此时快车在慢车的后
面).列表:
相等关系:慢车行驶的路程+1 500 km-快车行
驶的路程=1 200 km.
路程/km 速度/(km/h) 时间/h
慢车 60z 60 z
快车 90z 90 z
解:(1)设快车开出x h后两车相遇.
由题意,得
解得x=9.8.
答:快车开出9.8 h后两车相遇.
(2)设y h后两车相距1 800 km.
由题意,得60y+90y+1 500=1 800.
解得y=2.
答:2 h后两车相距1 800 km.
(3)设z h后两车相距1 200 km(此时快车在慢车的后面).
由题意,得60z+1 500-90z=1 200.
解得z=10.
答:10 h后两车相距1 200 km(此时快车在慢车
的后面).
(1)分析行程问题时,可借助图示、列表来分析数量
关系,图示可直观找出路程的相等关系,列表可
将路程、速度、时间的关系清晰地展示出来.
(2)本例是求时间,我们可设时间为未知数,从表中
求路程;如果要求的是路程,那么我们可设路程
为未知数,从表中求时间,其依据是路程、速度
总 结
2.顺流(风)、逆流(风)问题
航行问题中的基本关系式:
顺水(风)速度=静水(风)速度+水(风)速度.
逆水(风)速度=静水(风)速度-水(风)速度.
例5 一艘船从甲码头到乙码头顺流而行,用了 2 h;从乙码头返回甲码头逆流而行,用了 2.5 h,已知水流的速度是3 km/h,求船在静水中的平均速度.
分析:一般情况下可以认为这艘船往返的路程相等,
由此填空:
顺流速度________顺流时间________逆流速度 ________逆流时间.
×
=
×
解:设船在静水中的平均速度为x km/h,则顺流速
度为(x+3)km/h,逆流 速度为(x-3)km/k.根据往返路程相等,列得 2(x+3) =2. 5(x-3).
去括号,得2x+6=2.5x-7. 5.
移项及合并同类项,得0. 5x=13. 5.
系数化为1,得x=27.
答:船在静水中的平均速度为27 km/h.
(1)行程问题:虽然不同的问题有不同的关系式,但列表格分析的方式是一致的,在路程、速度、时
间这三个量中,已知量相同,设的未知量不同,所列方程也不同.
(2)解有关行程问题时,我们始终要记住一句话:在行程问题三个基本量(路程、速度、时间)中:
总 结
①如果速度已知,若从时间设元,则从路程找相等
关系列方程;若从路程设元,则从时间找相等关系
列方程;②如果时间已知,若从速度设元,则从路
程找相等关系列方程;若从路程设元,则从速度找
相等关系列方程;③如果路程已知,若从时间设元,
则从速度找相等关系列方程;若从速度设元,则从
时间找相等关系列方程.
3.上坡、下坡问题
例6 从甲地到乙地的路有一段平路与一段上坡路.
如果骑自行车保持平路每小时行15 km,上坡
路每小时行10 km,下坡路每小时行18 km,
那么从甲地到乙地需29 min,从乙地到甲地需
25 min.从甲地到乙地的路程是多少?
解:设在平路段所用的时间为x小时,
则依题意得:
解得 :
则从甲地到乙地的路程是
答:从甲地到乙地的路程是6.5 km.
课堂小结
1. 解一元一次方程的步骤:去括号→移项→合并同类项→系数化为1.
2. 若括号外的因数是负数,去括号时,原括
号内各项的符号要改变.
【课后练习】
1.下列方程有解的是( )
A.x-2=2-x B.x+2=x-2 C.2(x+1)=2x D.|x+2|=-3
2.关于x的方程a-3(x+5)=b(x+2)是关于x的一元一次方程,则( )
A.b=2 B.b=-3 C.b≠2 D.b≠-3
3.若方程2(2x+1)=3+3x的解与关于x的方程2k+6=2(x+3)的解相同,则k的值为( )
A.1 B.-1 C.7 D.-7
4.若代数式4x-7与代数式5(x-0.4)的值相等,则x的值是( )
A.-9 B.1 C.-5 D.3
5.将方程x﹣3(4﹣3x)=5去括号正确的是( )
A.x﹣12﹣6x=5B.x﹣12﹣2x=5C.x﹣12+9x=5D.x﹣3+6x=5
6.已知关于x的方程(a+1)x+(4a-1)=0的解为-2,则a的值为_________.
7.当x=___________时,式子3(x-2)和4(x+3)-4的值相等.
8.已知x=3是关于x的方程ax﹣5=9x﹣a的解,那么关于x的方程a(x﹣1)﹣5=9(x﹣1)﹣a的解是x=___.
9.方程2(x﹣1)=4的解是_____.
10.如果5x 5的值与2x 9的值互为相反数,那么x等于______.
【课后练习】答案
1.A 2.D 3.A 4.C 5.C
6.
7.-14
8.4
9.x=3
10.2
第三章 一元一次方程
3.3解一元一次方程(二)
第一课时
【学习目标】
1.了解“去括号”是解方程的重要步骤.
2.准确而熟练地运用去括号法则解带有括号的一元一次方程.
3.进一步培养学生分析解决问题的能力。
【课前预习】
1.在解方程3(x-1)-(x-3)=0 时,去括号正确的是( )
A.3x-1-x+3=0 B.3x-3-x-3=0 C.3x-1-x-3=0 D.3x-3-x+3=0
2.代数式a-2与1-2a的差是0,则a的值是( )
A.1 B.0 C.3 D.2
3.若方程2(2x-3)=1-3x的解与关于x的方程8-m=2(x+1)的解相同,则m的值为( )
A.-4 B.4 C.-12 D.12
4.解方程4.5(x+0.7)=9x,最简便的方法应该首先( )
A.去括号 B.方程两边同时乘以10 C.移项 D.方程两边同时除以4.5
5.当x=4时,式子5(x+m)-10与式子mx+4x的值相等,则m=( )
A.-2; B.2; C.4; D.6;
【课前预习】答案
1.D
2.A
3.B
4.D
5.D
化简下列各式:
(1) (-3a+2b) +3(a-b);
(2) -5a+4b-(-3a+b).
解:(1) 原式=-b;(2) 原式=-2a+3b.
复习回顾
去掉“+ ( )”,括号内各项的符号不变.
去掉“– ( )”,括号内各项的符号改变.
去括号法则:
用三个字母a,b,c表示去括号前后的变化规律:
a + (b + c) =
a -(b + c) =
a + b + c
a -b - c
移项,合并同类项,系数为化1,要注意什么?
②合并同类项时,只是把同类项的系数相加作为所得项的系数,字母部分不变。
③系数化为1,要方程两边同时除以未知数前面的系数。
①移项要变号。
★ 我们在方程6x-7=4x-1上加上一个括号得
6x-7=4(x-1)会解吗?
★ 再在前面再加上一个负号得6x-7=-4(x-1)
会解吗?
讨论
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 kW h (千瓦 时), 全年用电15万kW h. 这个工厂去年上半年每月平均用电是多少?
问 题
一、利用去括号解一元一次方程
设上半年每月平均用电x kW h,则下半年每月平均用电(x- 2 000) kW h; 上半年共用电6x kW h,下半年共用电6(x- 2 000) kW h.根据全年用电15万kW h,列得方程
6x+6(x- 2 000) =150 000.
如果去括号,就能简化方程的形式.
下面的框图表示了解这个方程的流程.
6x+6(x-2 000) =150 000
6x+6x-12 000 =150 000
6x+6x = 150 000+12 000
12x = 162 000
x = 13 500
去括号
移项
合并同类项
系数化为1
方程中有带括号的式子时,去括号是常用的化简步骤.
去括号的目的是能利用移项法解方程;其实质是
乘法的分配律.
例1 解下列方程:
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
典例精析
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
通过以上解方程的过程,你能总结出解含有括号的一元一次方程的一般步骤吗?
去括号
移项
合并同类项
系数化为1
解含有括号的一元一次方程时,要先利用前面学习的去括号法则去掉括号,再利用移项法解方程.
去括号解一元一次方程的步骤:
第一步:去括号(按照去括号法则去括号);
第二步:用移项法解这个一元一次方程:
移项→合并同类项→系数化为1.
移项,合并同类项,系数化为1,要注意什么?
②合并同类项时,只是把同类项的系数相加作为所得项的系数,字母部分不变.
③系数化为1,也就是说方程两边同时除以未知数前面的系数.
①移项时要变号.(变成相反数)
例2 解方程
3x-7(x-1)=3-2(x+3).
解:去括号,得:
3x-7x+7=3-2x -6.
移项得
3x-7x+2x =3-6-7.
合并同类项得
-2x=-10.
系数化为1,得
x=5.
例3 解方程:
导引:初看本例,我们可以利用去括号法解,但 我们只要仔细分析本例的特征,不难发现四个括号里,有两个(x+1)和两个(x-1),因此可先将它们各看作一个整体,再移项、合并进行解答.
解:移项,得
合并,得
去括号,得
移项,得
合并同类项,得-x=-4.
系数化为1,得x=4.
1. 一般行程问题
1. 行程问题中的基本关系式:
路程=速度×时间,
时间=路程÷速度,
速度=路程÷时间.
二、去括号解方程的应用
2. 行程问题中的相等关系:
(1)相遇问题中的相等关系:
①若甲、乙相向而行,甲走的路程+乙走的路程
=甲、乙出发点之间的路程;
②若甲、乙同时出发,甲用的时间=乙用的时间.
(2)追及问题中的相等关系:
①快者走的路程-慢者走的路程=追及路程;
②若同时出发,快者追上慢者时,快者用的时
间=慢者用的时间.
例4 甲站和乙站相距1 500 km,一列慢车从甲站开出,速度为60 km/h,一列快车从乙站开出,速度为90 km/h.
(1)若两车相向而行,慢车先开30 min,快车开出几小时后两车相遇?
(2)若两车同时开出,相背而行,多少小时后两
车相距1 800 km
(3)若两车同时开出,快车在慢车后面同向而行,
多少小时后两车相距1 200 km(此时快车在慢
车的后面)
导引:(1)设快车开出x h后两车相遇.列表:
相等关系:慢车行驶的路程+快车行驶的
路程=1 500 km.
路程/km 速度/(km/h) 时间/h
慢车 60
快车 90x 90 x
(2)设y h后两车相距1 800 km.列表:
相等关系:
两车行驶的路程和+1 500 km=1 800 km.
路程/km 速度/(km/h) 时间/h
慢车 60y 60 y
快车 90y 90 y
(3)设z h后两车相距1 200 km(此时快车在慢车的后
面).列表:
相等关系:慢车行驶的路程+1 500 km-快车行
驶的路程=1 200 km.
路程/km 速度/(km/h) 时间/h
慢车 60z 60 z
快车 90z 90 z
解:(1)设快车开出x h后两车相遇.
由题意,得
解得x=9.8.
答:快车开出9.8 h后两车相遇.
(2)设y h后两车相距1 800 km.
由题意,得60y+90y+1 500=1 800.
解得y=2.
答:2 h后两车相距1 800 km.
(3)设z h后两车相距1 200 km(此时快车在慢车的后面).
由题意,得60z+1 500-90z=1 200.
解得z=10.
答:10 h后两车相距1 200 km(此时快车在慢车
的后面).
(1)分析行程问题时,可借助图示、列表来分析数量
关系,图示可直观找出路程的相等关系,列表可
将路程、速度、时间的关系清晰地展示出来.
(2)本例是求时间,我们可设时间为未知数,从表中
求路程;如果要求的是路程,那么我们可设路程
为未知数,从表中求时间,其依据是路程、速度
总 结
2.顺流(风)、逆流(风)问题
航行问题中的基本关系式:
顺水(风)速度=静水(风)速度+水(风)速度.
逆水(风)速度=静水(风)速度-水(风)速度.
例5 一艘船从甲码头到乙码头顺流而行,用了 2 h;从乙码头返回甲码头逆流而行,用了 2.5 h,已知水流的速度是3 km/h,求船在静水中的平均速度.
分析:一般情况下可以认为这艘船往返的路程相等,
由此填空:
顺流速度________顺流时间________逆流速度 ________逆流时间.
×
=
×
解:设船在静水中的平均速度为x km/h,则顺流速
度为(x+3)km/h,逆流 速度为(x-3)km/k.根据往返路程相等,列得 2(x+3) =2. 5(x-3).
去括号,得2x+6=2.5x-7. 5.
移项及合并同类项,得0. 5x=13. 5.
系数化为1,得x=27.
答:船在静水中的平均速度为27 km/h.
(1)行程问题:虽然不同的问题有不同的关系式,但列表格分析的方式是一致的,在路程、速度、时
间这三个量中,已知量相同,设的未知量不同,所列方程也不同.
(2)解有关行程问题时,我们始终要记住一句话:在行程问题三个基本量(路程、速度、时间)中:
总 结
①如果速度已知,若从时间设元,则从路程找相等
关系列方程;若从路程设元,则从时间找相等关系
列方程;②如果时间已知,若从速度设元,则从路
程找相等关系列方程;若从路程设元,则从速度找
相等关系列方程;③如果路程已知,若从时间设元,
则从速度找相等关系列方程;若从速度设元,则从
时间找相等关系列方程.
3.上坡、下坡问题
例6 从甲地到乙地的路有一段平路与一段上坡路.
如果骑自行车保持平路每小时行15 km,上坡
路每小时行10 km,下坡路每小时行18 km,
那么从甲地到乙地需29 min,从乙地到甲地需
25 min.从甲地到乙地的路程是多少?
解:设在平路段所用的时间为x小时,
则依题意得:
解得 :
则从甲地到乙地的路程是
答:从甲地到乙地的路程是6.5 km.
课堂小结
1. 解一元一次方程的步骤:去括号→移项→合并同类项→系数化为1.
2. 若括号外的因数是负数,去括号时,原括
号内各项的符号要改变.
【课后练习】
1.下列方程有解的是( )
A.x-2=2-x B.x+2=x-2 C.2(x+1)=2x D.|x+2|=-3
2.关于x的方程a-3(x+5)=b(x+2)是关于x的一元一次方程,则( )
A.b=2 B.b=-3 C.b≠2 D.b≠-3
3.若方程2(2x+1)=3+3x的解与关于x的方程2k+6=2(x+3)的解相同,则k的值为( )
A.1 B.-1 C.7 D.-7
4.若代数式4x-7与代数式5(x-0.4)的值相等,则x的值是( )
A.-9 B.1 C.-5 D.3
5.将方程x﹣3(4﹣3x)=5去括号正确的是( )
A.x﹣12﹣6x=5B.x﹣12﹣2x=5C.x﹣12+9x=5D.x﹣3+6x=5
6.已知关于x的方程(a+1)x+(4a-1)=0的解为-2,则a的值为_________.
7.当x=___________时,式子3(x-2)和4(x+3)-4的值相等.
8.已知x=3是关于x的方程ax﹣5=9x﹣a的解,那么关于x的方程a(x﹣1)﹣5=9(x﹣1)﹣a的解是x=___.
9.方程2(x﹣1)=4的解是_____.
10.如果5x 5的值与2x 9的值互为相反数,那么x等于______.
【课后练习】答案
1.A 2.D 3.A 4.C 5.C
6.
7.-14
8.4
9.x=3
10.2
