5.7三角函数的应用课时练习-2021-2022学年高一数学上学期人教A版(2019)必修第一册(word含答案)
文档属性
| 名称 | 5.7三角函数的应用课时练习-2021-2022学年高一数学上学期人教A版(2019)必修第一册(word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 18:08:56 | ||
图片预览




文档简介
5.7三角函数的应用
一、单选题(共15 题)
1.风力发电不需要燃料 不占耕地 没有污染,运行成本低,所以产业发展前景非常广阔,在某风速时,传感器显示的电压按正弦规律变化,下表是时间和电压的相关数据,则风力发电的风叶转一圈的时间为( )
时间t(单位:) 0 0.1 0.2 0.3 0.4 0.5 0.6
电压U(单位:) 0 22 0 0 22 0
A.0.2 B.0.4 C.0.6 D.0.8
2.简谐运动的相位与初相分别是( )
A., B.,
C., D.,
3.函数f(x)=cosx·|tanx|在区间上的大致图象为( )
A. B.
C. D.
4.动点在圆上绕坐标原点作逆时针匀速圆周运动,旋转一周的时间恰好是12秒,已知时间时,点的坐标是,则动点的纵坐标关于(单位:秒)的函数在下列哪个区间上单调递增( )
A. B. C. D.
5.某市一年12个月的月平均气温与月份的关系可近似地用函数()来表示,已知该市6月份的平均气温最高,为,12月份的平均气温最低,为,则该市8月份的平均气温为( )
A. B. C. D.
6.某摩天轮建筑,其旋转半径50米,最高点距地面110米,运行一周大约21分钟.某人在最低点的位置坐上摩天轮,则第7分钟时他距地面大约为( )
A.75米 B.85米 C.100米 D.110米
7. 若函数的相邻两个零点的距离为,且,则函数的极值点为( )
A. B.
C. D.
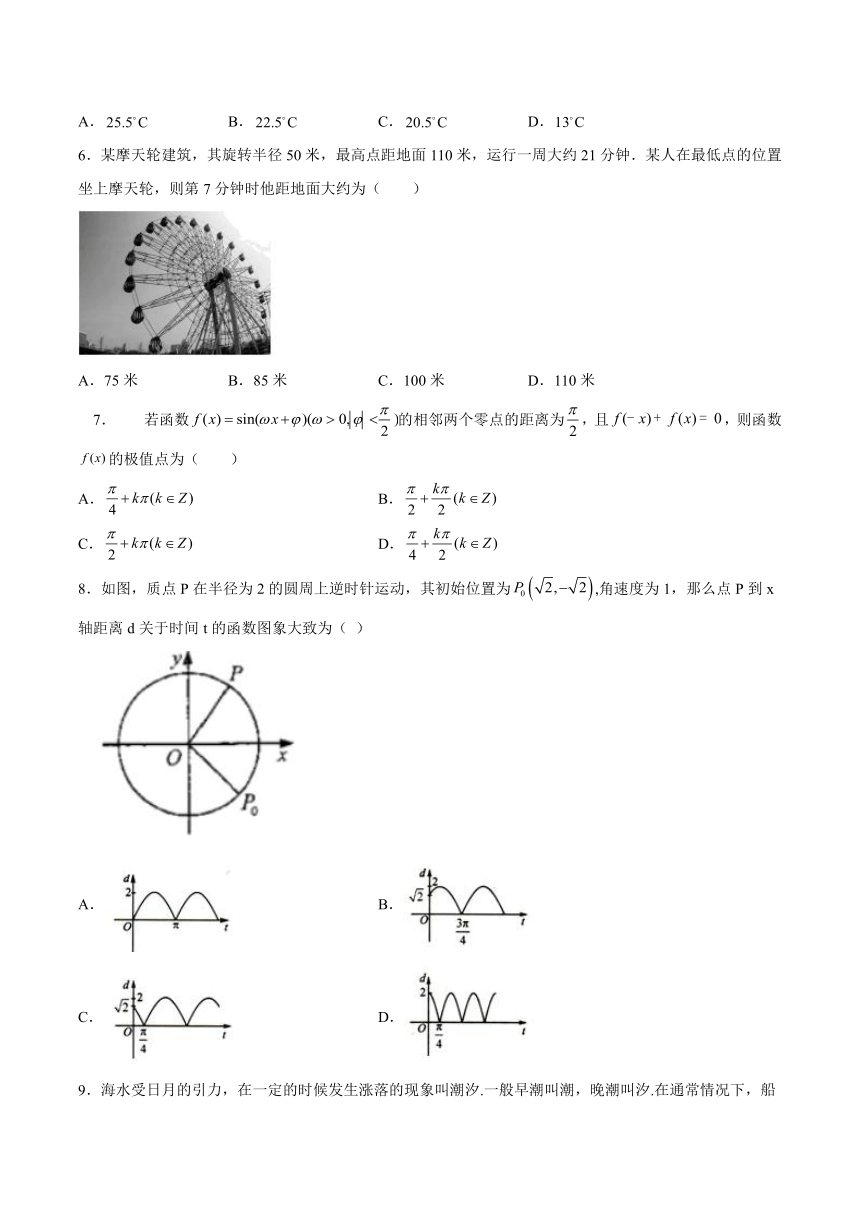
8.如图,质点P在半径为2的圆周上逆时针运动,其初始位置为,角速度为1,那么点P到x轴距离d关于时间t的函数图象大致为( )
A. B.
C. D.
9.海水受日月的引力,在一定的时候发生涨落的现象叫潮汐.一般早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮时返回海洋.下面是某港口在某季节每天的时间与水深值(单位:)记录表
时刻 0:00 3:00 6:00 9:00 12:00 15:00 18:00 21:00 24:00
水深值
已知港口的水的深度随时间变化符合函数,现有一条货船的吃水深度(船底与水面的距离)为,安全条例规定至少要有的安全间隙(船底与海底的距离),该船计划在中午点之后按规定驶入港口,并开始卸货,卸货时,其吃水深度以每小时的速度减小,小时卸完,则其在港口最多能停放( )
A.小时 B.小时 C.小时 D.小时
10.若两个函数的图象经过若干次平移后能够重合,则称这两个函数为“同形”函数,给出下列四个函数:,,,,则“同形”函数是( )
A.与 B.与 C.与 D.与
11.函数的部分图象如图所示,则下列叙述正确的是
A.函数的图象可由的图象向左平移个单位得到
B.函数的图象关于直线对称
C.函数在区间上是单调递增的
D.函数图象的对称中心为
12.第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如图,会标是由4个全等的直角三角形与一个小正方形拼成的一个大正方形,若小正方形的面积为4,大正方形的面积为100,设直角三角形中较大的锐角为,则( ).
A. B. C. D.
13.某艺术爱好者对《蒙娜丽莎》的同比例影像作品进行了测绘.将画中女子的嘴唇近似看作一个圆弧,在嘴角,处作圆弧的切线,两条切线交于点,测得如下数据:,,.根据测量得到的结果推算女子的嘴唇视作的圆弧对应的圆心角位于( )
A. B. C. D.
14.若函数在为增函数,则实数a的取值范围是
A. B.
C. D.
15.2020年3月14日是全球首个国际圆周率日( Day).历史上,求圆周率的方法有多种,与中国传统数学中的“割圆术”相似.数学家阿尔·卡西的方法是:当正整数充分大时,计算单位圆的内接正边形的周长和外切正边形(各边均与圆相切的正边形)的周长,将它们的算术平均数作为的近似值.按照阿尔·卡西的方法,的近似值的表达式是( ).
A. B.
C. D.
二、填空题(共4题)
16.圆的半径为,为圆周上一点,现将如图放置的边长为的正方形(实线所示 ,正方形的顶点和点重合)沿着圆周顺时针滚动,经过若干次滚动,点第一次回到点的位置,则点走过的路径的长度为_____.
17.如图,直线,垂足为O,已知中,为直角,AB=2,BC=1,该直角三角形做符合以下条件的自由运动:(1),(2).则C、O两点间的最大距离为______.
18.已知点,点是以原点为圆心,1为半径的圆上的任意一点,将点绕点逆时针旋转90°得点,线段的中点为,则的最大值是______
19.已知南北回归线的纬度为,设地球表面某地正午太阳高度角为,为此时太阳直射纬度,为该地的纬度值,那么这三个量之间的关系是.当地夏半年取正值,冬半年取负值,如果在北半球某地(纬度为)的一幢高为的楼房北面盖一新楼,要使新楼一层正午的太阳全年不被前面的楼房遮挡,两楼的距离应不小于______(结果用含有和的式子表示).
三、解答题(共5题)
20.天津海河永乐桥上的摩天轮被誉为“天津之眼”,是世界上唯一一座建在桥上的摩天轮.如图所示,该摩天轮直径为米,最高点距离地面米,相当于层楼高,摩天轮的圆周上均匀的安装了个透明座舱,每个座舱最多可坐人,整个摩天轮可同时供余人观光,并且运行时按逆时针匀速旋转,转一周需要分钟.
(1)某游客自最低点处登上摩天轮,请问分钟后他距离地面的高度是多少?
(2)若甲乙两游客分别坐在,两个座舱里,且他们之间间隔个座舱,求,两个座舱的直线距离;
(3)若游客在距离地面至少米的高度能够获得俯瞰天津市美景的最佳视觉效果,请问摩天轮转动一周能有多长时间会有这种最佳视觉效果.
21.某工厂制作如图所示的一种标识,在半径为R的圆内做一个关于圆心对称的“H型”图形,“H”型图形由两竖一横三个等宽的矩形组成,两个竖直的矩形全等且它们的长边是横向矩形长边的倍,设O为圆心,,“H”型图形的面积为S.
(1)将AB、AD用R、表示,并将S表示成的函数;
(2)为了突出“H”型图形,设计时应使S尽可能大,则当为何值时,S最大?并求出S的最大值.
22.某公园内有一块以O为圆心半径为20米的圆形区域.为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形OAB区域,其中两个端点A,B分别在圆周上;观众席为等腰梯形ABQP内且在圆O外的区域,其中,,且AB,PQ在点O的同侧.为保证视听效果,要求观众席内每一个观众到舞台中心O处的距离都不超过60米(即要求).设,.
(1)当时求舞台表演区域的面积;
(2)对于任意α,上述设计方案是否均能符合要求?
23.如图,某公园摩天轮的半径为40,圆心O距地面的高度为50,摩天轮做匀速转动,每3转一圈,摩天轮上的点P的起始位置在距地面最近处.
(1)已知在时点P距离地面的高度为,求时,点P距离地面的高度;
(2)当离地面以上时,可以看到公园的全貌,求转一圈中在点P处有多少时间可以看到公园的全貌.
24.已知的最小正周期为.
(1)若,求;
(2)若,,求的值.
参考答案
1.B
【详解】
观察表格信息可知:
电压从0到、从到0、从0到22、从22到0,四个过程是一个周期,
所以风力发电的风叶转一圈的时间为0.4,
故选:B
2.C
【详解】
相位是;当时的相位为初相,即.
故选:C
3.C
【详解】
,
故选:C.
4.D
【详解】
解:根据题意,
得,点每秒旋转,
所以秒旋转,,
则.
令,
解得:,
经检验:当时,,故D符合,
故选:D.
5.A
【详解】
由题意可得:
即,解得:,
所以,
所以该市8月份的平均气温为,
故选:A.
6.B
【详解】
设他与地面的高度与时间的关系为
,,,,
由题意可知,,,
,
即,
又,
即,
故,
,
(7).
故选:B.
7.D
【解析】
∵函数的相邻两个零点的距离为,∴,故,又∵,即函数为奇函数,故可得,结合得,故,∴,令,得,经检验为极值点,故选D.
8.C
【详解】
通过分析可知当时,点 到 轴距离为,于是可以排除答案A,D;
再根据当时,可知点 在 轴上此时点 到 轴距离 为 0 ,排除答案 B
故选C.
9.B
【详解】
由表格中的数据可知,,则.
由T=12,∴,故,
当x=3时,f(x)=7,则∴,即,得.
∴.
由,得,
即或
∴或.
又该船计划在中午12点之后按规定驶入港口,
∴k=1时,x=13,即该船应在13点入港并开始卸货,
卸货时,其吃水深度以每小时的速度减小,小时卸完,卸完后的吃水深度为,
所以该货船需要的安全水深为3+2=5米,由,得,
即或
∴或.
所以可以停留到18点,此时水深为5米,货船需要离港,则其在港口最多能停放5小时.
故选:B
10.D
【详解】
根据本题所给的信息:两个函数的图象经过若干次平移后能够重合,则称这两个函数为“同形”函数,所以,所选的两个函数最小正周期相等,振幅也相等.
,该函数的最小正周期为,振幅为;
,该函数的最小正周期为,振幅为;
,该函数的最小正周期为,振幅为;
,该函数的最小正周期为,振幅为.
所以要得到函数的图象,只需将函数的图象先向左平移个单位长度,再向下平移个单位长度即可.
故选:D.
11.D
【详解】
由图象可知A=2,f(0)=1,
∵f(0)=2sinφ=1,且,
∴,
∴f(x)=2sin(ωx),
∵f()=0且为单调递减时的零点,
∴,k∈Z,
∴,k∈Z,
由图象知,
∴ω,
又∵ω>0,
∴ω=2,
∴f(x)=2sin(2x),
∵函数f(x)的图象可由y=Asinωx的图象向左平移个单位得,
∴A错,
令2x,k∈Z,对称轴为x,则B错,
令2x,则x,则C错,
令2xkπ,k∈Z,则x=,则D对,
故选:D.
12.B
【详解】
解:根据题意,每个直角三角形的两条直角边的长度之差为2、斜边的长度为10,
故设直角三角形较大直角边为,则另一直角边为,
所以,解方程得:,
∴,,则,
∴.
故选:B.
13.B
【详解】
解:取,设
则
设《蒙娜丽莎》中女子的嘴唇视作的圆弧对应的圆心角为
则
故选:B
14.A
【详解】
由题意,当时,在区间不是单调函数,不符合题意;
当时,,其中,
要使得函数单调递增,则,即,
因为函数在区间上单调递增,
所以且,解得,
所以,即恒成立,所以,故选A.
15.A
【详解】
单位圆内接正边形的每条边所对应的圆心角为,每条边长为 ,
所以,单位圆的内接正边形的周长为,
单位圆的外切正边形的每条边长为,其周长为,
,
则.
故选:A.
16.
【解析】
试题分析:A走过的路径由9段圆心角均为的劣弧组成,其中6个劣弧所在圆的半径为1,3个劣弧所在圆的半径为,所以点A走过的路径的长度为.
考点:弧长公式.
17.
【解析】
试题分析:以为原点,为轴,为建立直角坐标系,如图所示,设,则有,,所以
,当时,最大,最大值为,则两点间的最大距离为.
考点:点、线、面间的距离的计算.
18.
【详解】
解:由题可知,设,则,
因为,所以线段的中点得坐标为,
所以
,其中,
因为,
所以当时,取最大值为.
故答案为:.
19.
【详解】
如图:
设点A,B,C分别为太阳直射北回归线,赤道,南回归线时楼顶在地面上得投射点,要使新楼一层正午的太阳全年不被前面的楼房遮挡,应取太阳直射南回归线时的情况考虑,此时的太阳直射纬度为,依题意两楼的间距不小于MC,根据太阳高度角的定义得:
故答案为:
20.(1)37.5米;(2);(3)分钟.
【详解】
(1)设摩天轮转动分钟()时游客的高度为,
摩天轮旋转一周需要分钟,所以座舱每分钟旋转角的大小为,
由题意可得,,
当时, ,
所以游客分钟后距离地面的高度是米 .
(2) 由题意可知,,
在中,,
(3)由题意可知,要获得俯瞰的最佳视觉效果,
应满足,
化简得,
因为,所以
所以 ,解得,
所以摩天轮旋转一周能有分钟最佳视觉效果.
21.(1),;;(2)时,.
【详解】
(1)如图所示:
设OM交CD于N,
因为,
所以,
所以,
所以,,
因为,所以,所以;
;
(2),
,
,
,
因为,所以,
所以,即时,S取得最大值.
22.(1)平方米(2)对于任意α,上述设计方案均能符合要求,详见解析
【详解】
(1)当时,
所以舞台表演区域的面积平方米
(2)
作于H,则
在中,
因为,所以当时,
所以对于任意α,上述设计方案均能符合要求.
23.(1)70;(2)0.5.
【详解】
(1)依题意,,,,
由得,所以.
因为,所以,又,所以.
所以,
所以.
即时点P距离地面的高度为70m.
(2)由(1)知.
令,即,
从而,
∴.
∵,
∴转一圈中在点P处有0.5min的时间可以看到公园的全貌.
24.(1);(2).
【解析】
试题分析:
(1)整理函数的解析式有:,则,结合三角函数的性质可得,,则.
(2)由题意可得,则,据此可得 .
试题解析:
(1) ,
由得,
所以,当时,有,
所以,所以,解得.
(2)因为,所以,
所以,
,
所以 .
一、单选题(共15 题)
1.风力发电不需要燃料 不占耕地 没有污染,运行成本低,所以产业发展前景非常广阔,在某风速时,传感器显示的电压按正弦规律变化,下表是时间和电压的相关数据,则风力发电的风叶转一圈的时间为( )
时间t(单位:) 0 0.1 0.2 0.3 0.4 0.5 0.6
电压U(单位:) 0 22 0 0 22 0
A.0.2 B.0.4 C.0.6 D.0.8
2.简谐运动的相位与初相分别是( )
A., B.,
C., D.,
3.函数f(x)=cosx·|tanx|在区间上的大致图象为( )
A. B.
C. D.
4.动点在圆上绕坐标原点作逆时针匀速圆周运动,旋转一周的时间恰好是12秒,已知时间时,点的坐标是,则动点的纵坐标关于(单位:秒)的函数在下列哪个区间上单调递增( )
A. B. C. D.
5.某市一年12个月的月平均气温与月份的关系可近似地用函数()来表示,已知该市6月份的平均气温最高,为,12月份的平均气温最低,为,则该市8月份的平均气温为( )
A. B. C. D.
6.某摩天轮建筑,其旋转半径50米,最高点距地面110米,运行一周大约21分钟.某人在最低点的位置坐上摩天轮,则第7分钟时他距地面大约为( )
A.75米 B.85米 C.100米 D.110米
7. 若函数的相邻两个零点的距离为,且,则函数的极值点为( )
A. B.
C. D.
8.如图,质点P在半径为2的圆周上逆时针运动,其初始位置为,角速度为1,那么点P到x轴距离d关于时间t的函数图象大致为( )
A. B.
C. D.
9.海水受日月的引力,在一定的时候发生涨落的现象叫潮汐.一般早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮时返回海洋.下面是某港口在某季节每天的时间与水深值(单位:)记录表
时刻 0:00 3:00 6:00 9:00 12:00 15:00 18:00 21:00 24:00
水深值
已知港口的水的深度随时间变化符合函数,现有一条货船的吃水深度(船底与水面的距离)为,安全条例规定至少要有的安全间隙(船底与海底的距离),该船计划在中午点之后按规定驶入港口,并开始卸货,卸货时,其吃水深度以每小时的速度减小,小时卸完,则其在港口最多能停放( )
A.小时 B.小时 C.小时 D.小时
10.若两个函数的图象经过若干次平移后能够重合,则称这两个函数为“同形”函数,给出下列四个函数:,,,,则“同形”函数是( )
A.与 B.与 C.与 D.与
11.函数的部分图象如图所示,则下列叙述正确的是
A.函数的图象可由的图象向左平移个单位得到
B.函数的图象关于直线对称
C.函数在区间上是单调递增的
D.函数图象的对称中心为
12.第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如图,会标是由4个全等的直角三角形与一个小正方形拼成的一个大正方形,若小正方形的面积为4,大正方形的面积为100,设直角三角形中较大的锐角为,则( ).
A. B. C. D.
13.某艺术爱好者对《蒙娜丽莎》的同比例影像作品进行了测绘.将画中女子的嘴唇近似看作一个圆弧,在嘴角,处作圆弧的切线,两条切线交于点,测得如下数据:,,.根据测量得到的结果推算女子的嘴唇视作的圆弧对应的圆心角位于( )
A. B. C. D.
14.若函数在为增函数,则实数a的取值范围是
A. B.
C. D.
15.2020年3月14日是全球首个国际圆周率日( Day).历史上,求圆周率的方法有多种,与中国传统数学中的“割圆术”相似.数学家阿尔·卡西的方法是:当正整数充分大时,计算单位圆的内接正边形的周长和外切正边形(各边均与圆相切的正边形)的周长,将它们的算术平均数作为的近似值.按照阿尔·卡西的方法,的近似值的表达式是( ).
A. B.
C. D.
二、填空题(共4题)
16.圆的半径为,为圆周上一点,现将如图放置的边长为的正方形(实线所示 ,正方形的顶点和点重合)沿着圆周顺时针滚动,经过若干次滚动,点第一次回到点的位置,则点走过的路径的长度为_____.
17.如图,直线,垂足为O,已知中,为直角,AB=2,BC=1,该直角三角形做符合以下条件的自由运动:(1),(2).则C、O两点间的最大距离为______.
18.已知点,点是以原点为圆心,1为半径的圆上的任意一点,将点绕点逆时针旋转90°得点,线段的中点为,则的最大值是______
19.已知南北回归线的纬度为,设地球表面某地正午太阳高度角为,为此时太阳直射纬度,为该地的纬度值,那么这三个量之间的关系是.当地夏半年取正值,冬半年取负值,如果在北半球某地(纬度为)的一幢高为的楼房北面盖一新楼,要使新楼一层正午的太阳全年不被前面的楼房遮挡,两楼的距离应不小于______(结果用含有和的式子表示).
三、解答题(共5题)
20.天津海河永乐桥上的摩天轮被誉为“天津之眼”,是世界上唯一一座建在桥上的摩天轮.如图所示,该摩天轮直径为米,最高点距离地面米,相当于层楼高,摩天轮的圆周上均匀的安装了个透明座舱,每个座舱最多可坐人,整个摩天轮可同时供余人观光,并且运行时按逆时针匀速旋转,转一周需要分钟.
(1)某游客自最低点处登上摩天轮,请问分钟后他距离地面的高度是多少?
(2)若甲乙两游客分别坐在,两个座舱里,且他们之间间隔个座舱,求,两个座舱的直线距离;
(3)若游客在距离地面至少米的高度能够获得俯瞰天津市美景的最佳视觉效果,请问摩天轮转动一周能有多长时间会有这种最佳视觉效果.
21.某工厂制作如图所示的一种标识,在半径为R的圆内做一个关于圆心对称的“H型”图形,“H”型图形由两竖一横三个等宽的矩形组成,两个竖直的矩形全等且它们的长边是横向矩形长边的倍,设O为圆心,,“H”型图形的面积为S.
(1)将AB、AD用R、表示,并将S表示成的函数;
(2)为了突出“H”型图形,设计时应使S尽可能大,则当为何值时,S最大?并求出S的最大值.
22.某公园内有一块以O为圆心半径为20米的圆形区域.为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形OAB区域,其中两个端点A,B分别在圆周上;观众席为等腰梯形ABQP内且在圆O外的区域,其中,,且AB,PQ在点O的同侧.为保证视听效果,要求观众席内每一个观众到舞台中心O处的距离都不超过60米(即要求).设,.
(1)当时求舞台表演区域的面积;
(2)对于任意α,上述设计方案是否均能符合要求?
23.如图,某公园摩天轮的半径为40,圆心O距地面的高度为50,摩天轮做匀速转动,每3转一圈,摩天轮上的点P的起始位置在距地面最近处.
(1)已知在时点P距离地面的高度为,求时,点P距离地面的高度;
(2)当离地面以上时,可以看到公园的全貌,求转一圈中在点P处有多少时间可以看到公园的全貌.
24.已知的最小正周期为.
(1)若,求;
(2)若,,求的值.
参考答案
1.B
【详解】
观察表格信息可知:
电压从0到、从到0、从0到22、从22到0,四个过程是一个周期,
所以风力发电的风叶转一圈的时间为0.4,
故选:B
2.C
【详解】
相位是;当时的相位为初相,即.
故选:C
3.C
【详解】
,
故选:C.
4.D
【详解】
解:根据题意,
得,点每秒旋转,
所以秒旋转,,
则.
令,
解得:,
经检验:当时,,故D符合,
故选:D.
5.A
【详解】
由题意可得:
即,解得:,
所以,
所以该市8月份的平均气温为,
故选:A.
6.B
【详解】
设他与地面的高度与时间的关系为
,,,,
由题意可知,,,
,
即,
又,
即,
故,
,
(7).
故选:B.
7.D
【解析】
∵函数的相邻两个零点的距离为,∴,故,又∵,即函数为奇函数,故可得,结合得,故,∴,令,得,经检验为极值点,故选D.
8.C
【详解】
通过分析可知当时,点 到 轴距离为,于是可以排除答案A,D;
再根据当时,可知点 在 轴上此时点 到 轴距离 为 0 ,排除答案 B
故选C.
9.B
【详解】
由表格中的数据可知,,则.
由T=12,∴,故,
当x=3时,f(x)=7,则∴,即,得.
∴.
由,得,
即或
∴或.
又该船计划在中午12点之后按规定驶入港口,
∴k=1时,x=13,即该船应在13点入港并开始卸货,
卸货时,其吃水深度以每小时的速度减小,小时卸完,卸完后的吃水深度为,
所以该货船需要的安全水深为3+2=5米,由,得,
即或
∴或.
所以可以停留到18点,此时水深为5米,货船需要离港,则其在港口最多能停放5小时.
故选:B
10.D
【详解】
根据本题所给的信息:两个函数的图象经过若干次平移后能够重合,则称这两个函数为“同形”函数,所以,所选的两个函数最小正周期相等,振幅也相等.
,该函数的最小正周期为,振幅为;
,该函数的最小正周期为,振幅为;
,该函数的最小正周期为,振幅为;
,该函数的最小正周期为,振幅为.
所以要得到函数的图象,只需将函数的图象先向左平移个单位长度,再向下平移个单位长度即可.
故选:D.
11.D
【详解】
由图象可知A=2,f(0)=1,
∵f(0)=2sinφ=1,且,
∴,
∴f(x)=2sin(ωx),
∵f()=0且为单调递减时的零点,
∴,k∈Z,
∴,k∈Z,
由图象知,
∴ω,
又∵ω>0,
∴ω=2,
∴f(x)=2sin(2x),
∵函数f(x)的图象可由y=Asinωx的图象向左平移个单位得,
∴A错,
令2x,k∈Z,对称轴为x,则B错,
令2x,则x,则C错,
令2xkπ,k∈Z,则x=,则D对,
故选:D.
12.B
【详解】
解:根据题意,每个直角三角形的两条直角边的长度之差为2、斜边的长度为10,
故设直角三角形较大直角边为,则另一直角边为,
所以,解方程得:,
∴,,则,
∴.
故选:B.
13.B
【详解】
解:取,设
则
设《蒙娜丽莎》中女子的嘴唇视作的圆弧对应的圆心角为
则
故选:B
14.A
【详解】
由题意,当时,在区间不是单调函数,不符合题意;
当时,,其中,
要使得函数单调递增,则,即,
因为函数在区间上单调递增,
所以且,解得,
所以,即恒成立,所以,故选A.
15.A
【详解】
单位圆内接正边形的每条边所对应的圆心角为,每条边长为 ,
所以,单位圆的内接正边形的周长为,
单位圆的外切正边形的每条边长为,其周长为,
,
则.
故选:A.
16.
【解析】
试题分析:A走过的路径由9段圆心角均为的劣弧组成,其中6个劣弧所在圆的半径为1,3个劣弧所在圆的半径为,所以点A走过的路径的长度为.
考点:弧长公式.
17.
【解析】
试题分析:以为原点,为轴,为建立直角坐标系,如图所示,设,则有,,所以
,当时,最大,最大值为,则两点间的最大距离为.
考点:点、线、面间的距离的计算.
18.
【详解】
解:由题可知,设,则,
因为,所以线段的中点得坐标为,
所以
,其中,
因为,
所以当时,取最大值为.
故答案为:.
19.
【详解】
如图:
设点A,B,C分别为太阳直射北回归线,赤道,南回归线时楼顶在地面上得投射点,要使新楼一层正午的太阳全年不被前面的楼房遮挡,应取太阳直射南回归线时的情况考虑,此时的太阳直射纬度为,依题意两楼的间距不小于MC,根据太阳高度角的定义得:
故答案为:
20.(1)37.5米;(2);(3)分钟.
【详解】
(1)设摩天轮转动分钟()时游客的高度为,
摩天轮旋转一周需要分钟,所以座舱每分钟旋转角的大小为,
由题意可得,,
当时, ,
所以游客分钟后距离地面的高度是米 .
(2) 由题意可知,,
在中,,
(3)由题意可知,要获得俯瞰的最佳视觉效果,
应满足,
化简得,
因为,所以
所以 ,解得,
所以摩天轮旋转一周能有分钟最佳视觉效果.
21.(1),;;(2)时,.
【详解】
(1)如图所示:
设OM交CD于N,
因为,
所以,
所以,
所以,,
因为,所以,所以;
;
(2),
,
,
,
因为,所以,
所以,即时,S取得最大值.
22.(1)平方米(2)对于任意α,上述设计方案均能符合要求,详见解析
【详解】
(1)当时,
所以舞台表演区域的面积平方米
(2)
作于H,则
在中,
因为,所以当时,
所以对于任意α,上述设计方案均能符合要求.
23.(1)70;(2)0.5.
【详解】
(1)依题意,,,,
由得,所以.
因为,所以,又,所以.
所以,
所以.
即时点P距离地面的高度为70m.
(2)由(1)知.
令,即,
从而,
∴.
∵,
∴转一圈中在点P处有0.5min的时间可以看到公园的全貌.
24.(1);(2).
【解析】
试题分析:
(1)整理函数的解析式有:,则,结合三角函数的性质可得,,则.
(2)由题意可得,则,据此可得 .
试题解析:
(1) ,
由得,
所以,当时,有,
所以,所以,解得.
(2)因为,所以,
所以,
,
所以 .
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
