北师大版八年级数学上册第二章《二次根式》复习课件(共21张PPT)
文档属性
| 名称 | 北师大版八年级数学上册第二章《二次根式》复习课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 475.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 09:23:04 | ||
图片预览








文档简介
(共21张PPT)
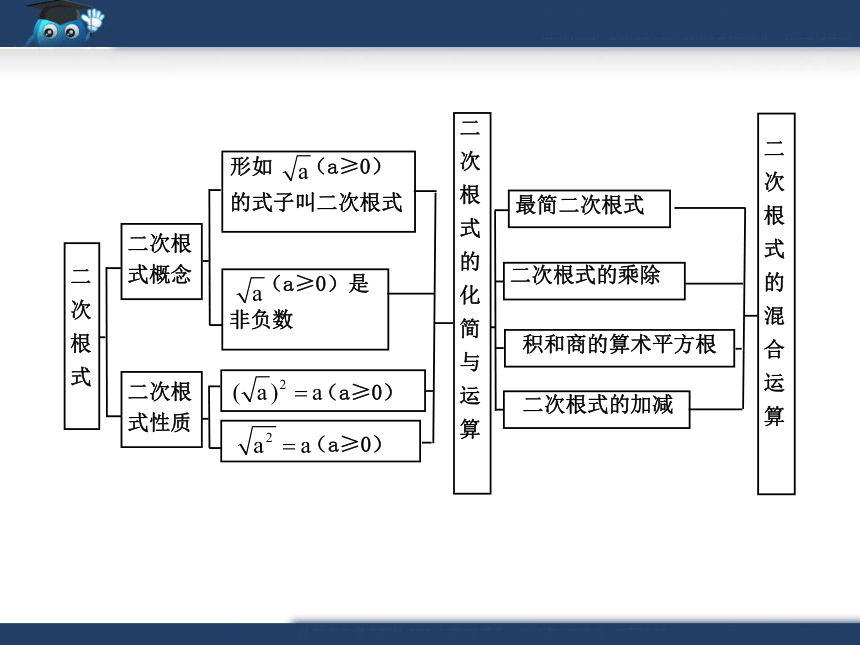
二次根式
二
次
根
式
二次根
式概念
二次根
式性质
形如 (a≥0)
的式子叫二次根式
(a≥0)是
非负数
(a≥0)
(a≥0)
二
次
根
式的化简与运算
最简二次根式
二次根式的乘除
积和商的算术平方根
二次根式的加减
二
次
根
式的混合运算
重点知识一 二次根式的定义及性质
二次根式的概念主要涉及两个非负性,即
中的a≥0, ≥0;二次根式的性质主要涉及( )2=
a(a≥0)、 (a≥0).
【例1】(黄石中考)已知x<1,则 化简的
结果是( )
(A)x-1 (B)x+1 (C)-x-1 (D)1-x
【思路点拨】 → 的形式 →
判断a的符号化简
【解析】选D.∵ x<1.
∴x-1<0.∴
重点知识二 二次根式的乘除及最简二次根式
二次根式的乘除主要涉及
两个法则,逆运用二次根式的乘
除法法则,结合二次根式的性质可将二次根式化为最简二次
根式(不含分母、不含开得尽方的因数或因式),注意结果的
分母中不能含有根号.
【例2】(乌鲁木齐中考)计算:
【思路点拨】将括号内的各代数式化为最简二次根式 →
合并 → 除法
(或 除法 → 将各代数式化为最简二次根式 → 合并 )
【解析】
重点知识三 二次根式的加减及其混合运算
首先要会二次根式的化简,能将一个二次根式化为最简二次根式;其次要分清运算顺序,先乘方、再乘除,最后加减,有括号的先算括号里面的;最后注意将结果化为最简.在运算的过程中要能合理地利用运算律和乘法公式简化运算.
【例3】(湘潭中考)先化简,再求值:
【思路点拨】 先化简 → 再代入求值 .
【解析】
重点知识一:二次根式的定义及性质
1.(无锡中考)使 有意义的x的取值范围是( )
(A)x> (B)x>-
(C)x≥ (D)x≥-
【解析】选C.根式有意义需3x-1≥0,所以x≥ .
2.(荆门中考)若a、b为实数,且满足│a-2│+ =0,则b-a的值为( )
(A)2 (B)0
(C)-2 (D)以上都不对
【解析】选C.根据非负性知a=2,b=0,则b-a=-2.
3.(武汉中考)二次根式 的值是( )
(A)-3 (B)3或-3 (C)9 (D)3
【解析】选D.
4.(黔东南州中考) =_______.
【解析】据算术平方根的意义得到结论,
即
答案:|x|
重点知识二:二次根式的乘除及最简二次根式
5.(贺州中考)下列根式中不是最简二次根式的是( )
【解析】选C.∵
6.(襄樊中考)计算 的结果估计在( )
(A)6至7之间 (B)7至8之间
(C)8至9之间 (D)9至10之间
【解析】选B.
∵3< <4,∴4+3<4+ <4+4.即7<4+ <8.
7.(德化中考)化简:
【解析】原式=
重点知识三:二次根式的加减及其混合运算
8.(新疆建设兵团中考)化简 =________.
【解析】
答案:
9.(日照中考)计算:
【解析】原式=
10.(东营中考)先化简,再求值:
【解析】
11.(烟台中考)化简:
【解析】
二次根式
二
次
根
式
二次根
式概念
二次根
式性质
形如 (a≥0)
的式子叫二次根式
(a≥0)是
非负数
(a≥0)
(a≥0)
二
次
根
式的化简与运算
最简二次根式
二次根式的乘除
积和商的算术平方根
二次根式的加减
二
次
根
式的混合运算
重点知识一 二次根式的定义及性质
二次根式的概念主要涉及两个非负性,即
中的a≥0, ≥0;二次根式的性质主要涉及( )2=
a(a≥0)、 (a≥0).
【例1】(黄石中考)已知x<1,则 化简的
结果是( )
(A)x-1 (B)x+1 (C)-x-1 (D)1-x
【思路点拨】 → 的形式 →
判断a的符号化简
【解析】选D.∵ x<1.
∴x-1<0.∴
重点知识二 二次根式的乘除及最简二次根式
二次根式的乘除主要涉及
两个法则,逆运用二次根式的乘
除法法则,结合二次根式的性质可将二次根式化为最简二次
根式(不含分母、不含开得尽方的因数或因式),注意结果的
分母中不能含有根号.
【例2】(乌鲁木齐中考)计算:
【思路点拨】将括号内的各代数式化为最简二次根式 →
合并 → 除法
(或 除法 → 将各代数式化为最简二次根式 → 合并 )
【解析】
重点知识三 二次根式的加减及其混合运算
首先要会二次根式的化简,能将一个二次根式化为最简二次根式;其次要分清运算顺序,先乘方、再乘除,最后加减,有括号的先算括号里面的;最后注意将结果化为最简.在运算的过程中要能合理地利用运算律和乘法公式简化运算.
【例3】(湘潭中考)先化简,再求值:
【思路点拨】 先化简 → 再代入求值 .
【解析】
重点知识一:二次根式的定义及性质
1.(无锡中考)使 有意义的x的取值范围是( )
(A)x> (B)x>-
(C)x≥ (D)x≥-
【解析】选C.根式有意义需3x-1≥0,所以x≥ .
2.(荆门中考)若a、b为实数,且满足│a-2│+ =0,则b-a的值为( )
(A)2 (B)0
(C)-2 (D)以上都不对
【解析】选C.根据非负性知a=2,b=0,则b-a=-2.
3.(武汉中考)二次根式 的值是( )
(A)-3 (B)3或-3 (C)9 (D)3
【解析】选D.
4.(黔东南州中考) =_______.
【解析】据算术平方根的意义得到结论,
即
答案:|x|
重点知识二:二次根式的乘除及最简二次根式
5.(贺州中考)下列根式中不是最简二次根式的是( )
【解析】选C.∵
6.(襄樊中考)计算 的结果估计在( )
(A)6至7之间 (B)7至8之间
(C)8至9之间 (D)9至10之间
【解析】选B.
∵3< <4,∴4+3<4+ <4+4.即7<4+ <8.
7.(德化中考)化简:
【解析】原式=
重点知识三:二次根式的加减及其混合运算
8.(新疆建设兵团中考)化简 =________.
【解析】
答案:
9.(日照中考)计算:
【解析】原式=
10.(东营中考)先化简,再求值:
【解析】
11.(烟台中考)化简:
【解析】
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
