河南省焦作市县级重点中学2021-2022学年高三上学期期中考试文科数学试题(Word含答案解析)
文档属性
| 名称 | 河南省焦作市县级重点中学2021-2022学年高三上学期期中考试文科数学试题(Word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 514.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 10:33:06 | ||
图片预览




文档简介
2021-2022学年河南省焦作市县级重点中学高三(上)期中联考数学试卷(文科)(附教师版答案详细解析)
一、选择题(本大题共12小题,每小题5分,共60分)
1.(5分)设a,b∈R,集合{1,a+b,a}={0,,b},则b﹣a=( )
A.1 B.﹣1 C.2 D.﹣2
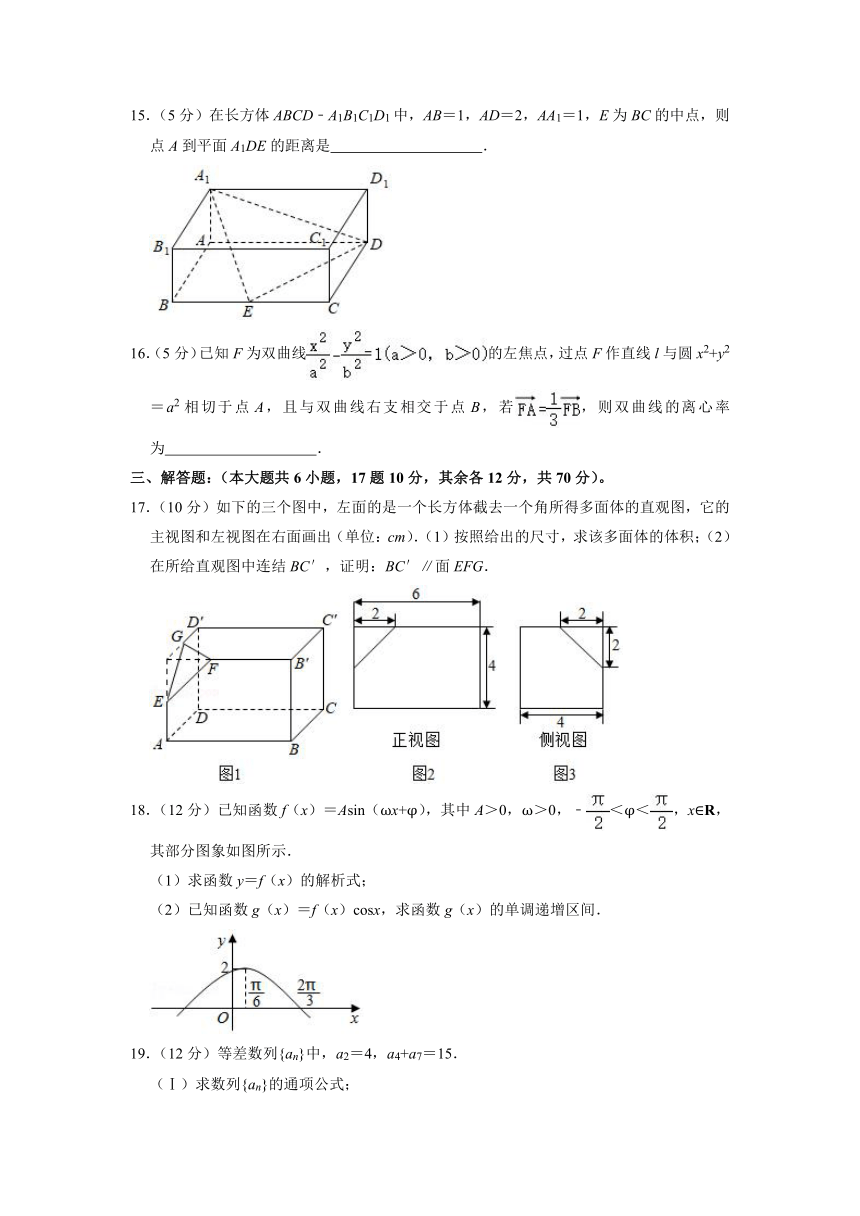
2.(5分)集合A={x|y=},B={y|y=2x,x>0},则A∩B=( )
A.[0,2] B.(1,2] C.[1,2] D.(1,+∞)
3.(5分)已知﹣<α<0,sinα+cosα=,则的值为( )
A. B. C. D.
4.(5分)在某种新型材料的研制中,实验人员获得了下列一组实验数据:现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是( )
x 1.992 3 4 5.15 6.126
y 1.517 4.0418 7.5 12 18.01
A.y=2x﹣2 B.y=(x2﹣1) C.y=log2x D.y=x
5.(5分)已知函数f(x)=,若互不相等的实数x1,x2,x3满足f(x1)=f(x2)=f(x3),则x1+x2+x3的取值范围为( )
A.() B.(﹣,) C.(,6] D.(﹣,]
6.(5分)函数f(x)=sin(2x+)向右平移φ(0≤φ≤π)个单位后得到函数g(x),若g(x)在(﹣,)上单调递增,则φ的取值范围是( )
A.[0,] B.[0,] C.[,] D.[,]
7.(5分)某几何体的三视图如图所示,则该几何体的外接球的球面面积为( )
A.5π B.12π C.20π D.8π
8.(5分)已知函数f(x)是定义在R上的偶函数,且在(﹣∞,0)上单调递减,若,b=f(log24.1),c=f(20.8),则a,b,c的大小关系是( )
A.a<b<c B.b<a<c C.c<a<b D.c<b<a
9.(5分)下列选项叙述错误的是( )
A.命题“若x≠1,则x2﹣3x+2≠0”的逆否命题是“若x2﹣3x+2=0,则x=1”
B.若命题p:x∈A∩B,则命题¬p是x A或x B
C.若p∨q为真命题,则p,q均为真命题
D.“x>2”是“x2﹣3x+2>0”的充分不必要条件
10.(5分)函数y=loga(x+3)﹣1(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny+2=0上(其中m,n>0),则的最小值等于( )
A.10 B.8 C.6 D.4
11.(5分)已知f(x)是定义在R上的偶函数,对任意的x∈R,都有f(2+x)=﹣f(x),且当x∈[0,1]时f(x)=﹣x2+1,则方程f(x)=k,k∈[0,1)在[﹣1,5]的所有实根之和为( )
A.0 B.2 C.4 D.8
12.(5分)设函数f'(x)是定义在(0,π)上的函数f(x)的导函数,有f'(x)cosx﹣f(x)sinx>0,若,,则a,b,c的大小关系是( )
A.a<b<c B.b<c<a C.c<b<a D.c<a<b
二、填空题(本大题共4小题,共20分)
13.(5分)已知f(x+1)是定义域为R的偶函数,对于任意x1,x2∈(﹣∞,1]且x1≠x2,都有,且f(3)=0,则的解集为 .
14.(5分)已知F为抛物线C:y2=x的焦点,点A,B在抛物线上,且分别位于x轴的上、下两侧,若△BFO的面积是(O为坐标原点),且=12,则直线AB的斜率是 .
15.(5分)在长方体ABCD﹣A1B1C1D1中,AB=1,AD=2,AA1=1,E为BC的中点,则点A到平面A1DE的距离是 .
16.(5分)已知F为双曲线的左焦点,过点F作直线l与圆x2+y2=a2相切于点A,且与双曲线右支相交于点B,若,则双曲线的离心率为 .
三、解答题:(本大题共6小题,17题10分,其余各12分,共70分)。
17.(10分)如下的三个图中,左面的是一个长方体截去一个角所得多面体的直观图,它的主视图和左视图在右面画出(单位:cm).(1)按照给出的尺寸,求该多面体的体积;(2)在所给直观图中连结BC′,证明:BC′∥面EFG.
18.(12分)已知函数f(x)=Asin(ωx+φ),其中A>0,ω>0,﹣<φ<,x∈R,其部分图象如图所示.
(1)求函数y=f(x)的解析式;
(2)已知函数g(x)=f(x)cosx,求函数g(x)的单调递增区间.
19.(12分)等差数列{an}中,a2=4,a4+a7=15.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=+n,求b1+b2+b3+…+b10的值.
20.(12分)在△ABC中,a,b,c分别是角A,B,C的对边,已知(sinA+sinB)2﹣sin2C=3sinAsinB.
(1)求角C;
(2)若b=4,且△ABC为锐角三角形,求△ABC面积的取值范围.
21.(12分)设函数f(x)=(a,b>0).
(1)若函数f(x)在x=1处的切线方程是bx+4y﹣3=0,求实数a,b的值;
(2)在(1)的条件下,若2(x﹣k)f(x)≥lnx对于0<x≤1恒成立,求实数k的取值范围.
22.(12分)已知数列{an}是首项为正数的等差数列,数列{}的前n项和为.
(1)求数列{an}的通项公式;
(2)设bn=(an+1) 2an,求数列{bn}的前n项和Tn.
2021-2022学年河南省焦作市县级重点中学高三(上)期中联考
数学试卷(文科)
参考答案与试题解析
一、选择题(本大题共12小题,每小题5分,共60分)
1.(5分)设a,b∈R,集合{1,a+b,a}={0,,b},则b﹣a=( )
A.1 B.﹣1 C.2 D.﹣2
【分析】根据题意,集合,注意到后面集合中有元素0,由集合相等的意义,结合集合中元素的特征,可得a+b=0,进而分析可得a、b的值,计算可得答案.
【解答】解:根据题意,集合,
又∵a≠0,
∴a+b=0,即a=﹣b,
∴,
b=1;
故a=﹣1,b=1,
则b﹣a=2,
故选:C.
2.(5分)集合A={x|y=},B={y|y=2x,x>0},则A∩B=( )
A.[0,2] B.(1,2] C.[1,2] D.(1,+∞)
【分析】先分别求出集合A,B,由此能求出A∩B.
【解答】解:∵集合={x|0≤x≤2}.
B={y|y=2x,x>0}={y|y>1},
∴A∩B={x|1<x≤2}=(1,2].
故选:B.
3.(5分)已知﹣<α<0,sinα+cosα=,则的值为( )
A. B. C. D.
【分析】先求出sin2α,再求出cos2α,即可求出的值.
【解答】解:∵sinα+cosα=,
∴1+2sinαcosα=,
∴sin2α=﹣,
∵﹣<α<0,sinα+cosα=,
∴﹣π<2α<0,|sinα|<|cosα|,
∴cos2α=,
∴==,
故选:C.
4.(5分)在某种新型材料的研制中,实验人员获得了下列一组实验数据:现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是( )
x 1.992 3 4 5.15 6.126
y 1.517 4.0418 7.5 12 18.01
A.y=2x﹣2 B.y=(x2﹣1) C.y=log2x D.y=x
【分析】由表中的数据分析得出,自变量基本上是等速增加,相应的函数值增加的速度越来越快,结合基本初等函数的图象与性质,利用排除法即可得出正确的答案.
【解答】解:由题意得,表中数据y随x的变化趋势,函数在(0,+∞)上是增函数,
且y的变化随x的增大越来越快;
∵A中函数是线性增加的函数,C中函数是比线性增加还缓慢的函数,D中函数是减函数;
∴排除A,C、D答案;
∴B中函数y=(x2﹣1)符合题意.
故选:B.
5.(5分)已知函数f(x)=,若互不相等的实数x1,x2,x3满足f(x1)=f(x2)=f(x3),则x1+x2+x3的取值范围为( )
A.() B.(﹣,) C.(,6] D.(﹣,]
【分析】先作出函数f(x)=的图象,如图,不妨设x1<x2<x3,则x2,x3关于直线x=3对称,得到x2+x3=6,且﹣<x1<0;最后结合求得x1+x2+x3的取值范围即可.
【解答】解:函数f(x)=的图象,如图,
不妨设x1<x2<x3,则x2,x3关于直线x=3对称,故x2+x3=6,
且x1满足﹣<x1<0;
则x1+x2+x3的取值范围是:﹣+6<x1+x2+x3<0+6;
即x1+x2+x3∈(,6).
故选:A.
6.(5分)函数f(x)=sin(2x+)向右平移φ(0≤φ≤π)个单位后得到函数g(x),若g(x)在(﹣,)上单调递增,则φ的取值范围是( )
A.[0,] B.[0,] C.[,] D.[,]
【分析】利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再利用正弦函数的单调性,求得φ的取值范围.
【解答】解:把函数f(x)=sin(2x+)向右平移φ(0≤φ≤π)个单位后得到函数g(x)=sin(2x﹣2φ+)的图象,
若g(x)在(﹣,)上单调递增,则﹣﹣2φ+≥﹣,且 ﹣2φ+≤,
求得≤φ≤,
故选:D.
7.(5分)某几何体的三视图如图所示,则该几何体的外接球的球面面积为( )
A.5π B.12π C.20π D.8π
【分析】三视图复原的几何体是底面为长、宽分别为3,4的长方形,侧棱垂直于底面的四棱锥;把它扩展为长方体,它的外接球的直径就是长方体的对角线的长,求出对角线长,即可求出外接球的表面积.
【解答】解:三视图复原的几何体是底面为长、宽分别为3,4的长方形,侧棱垂直于底面的四棱锥;把它扩展为长方体,
则长、宽、高分别为1,1,,
则它的外接球的直径就是长方体的对角线的长,
所以长方体的对角线长为:=
所以球的半径为:R=.
这个几何体的外接球的表面积是:4πR2=5π.
故选:A.
8.(5分)已知函数f(x)是定义在R上的偶函数,且在(﹣∞,0)上单调递减,若,b=f(log24.1),c=f(20.8),则a,b,c的大小关系是( )
A.a<b<c B.b<a<c C.c<a<b D.c<b<a
【分析】由奇偶性将数转化为(0,+∞)上,然后根据单调性比较大小.
【解答】解:由于f(x)为偶函数,则=f(﹣log25)=f(log25),
∵,函数f(x)是定义在R上的偶函数,且在(﹣∞,0)上单调递减
∴函数f(x)在(0,+∞)上单调递增,
∴>b=f(log24.1)>c=f(20.8),
故选:D.
9.(5分)下列选项叙述错误的是( )
A.命题“若x≠1,则x2﹣3x+2≠0”的逆否命题是“若x2﹣3x+2=0,则x=1”
B.若命题p:x∈A∩B,则命题¬p是x A或x B
C.若p∨q为真命题,则p,q均为真命题
D.“x>2”是“x2﹣3x+2>0”的充分不必要条件
【分析】利用逆否命题判断A的正误;命题的否定判断B的正误;或命题的真假判断C的正误;充要条件判断D的正误;
【解答】解:对于A,命题“若x≠1,则x2﹣3x+2≠0”的逆否命题是“若x2﹣3x+2=0,则x=1”,满足逆否命题的形式,所以A正确;
对于B,若命题p:x∈A∩B,则命题¬p是x A或x B,满足命题的否定的形式,所以B正确;
对于C,若p∨q为真命题,则p,q一真即可,说p,q均为真命题,不正确,所以C不正确;
对于D,“x>2”是“x2﹣3x+2>0”的充分不必要条件,前者能够说明后者,后者推不出前者,所以D正确;
故选:C.
10.(5分)函数y=loga(x+3)﹣1(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny+2=0上(其中m,n>0),则的最小值等于( )
A.10 B.8 C.6 D.4
【分析】先求出定点A的坐标,再把A代入直线方程,利用基本不等式求得的最小值.
【解答】解:令x+3=1,求得x=﹣2,可得函数y=loga(x+3)﹣1(a>0,且a≠1)的图象恒过定点A(﹣2,﹣1),
若点A在直线mx+ny+2=0上(其中m,n>0),则﹣2m﹣n+2=0,即 2m+n=2.
由基本不等式可得2≥2,即mn≤,即≥2,当且仅当2m=n=1时,取等号.
则==≥4,
故选:D.
11.(5分)已知f(x)是定义在R上的偶函数,对任意的x∈R,都有f(2+x)=﹣f(x),且当x∈[0,1]时f(x)=﹣x2+1,则方程f(x)=k,k∈[0,1)在[﹣1,5]的所有实根之和为( )
A.0 B.2 C.4 D.8
【分析】由f(x+2)=﹣f(x),可知f(x)是周期为4的周期函数.再由f(x)是偶函数,当x∈[0,1]时,f(x)=﹣x2+1,可得函数在[﹣1,5]上的解析式.利用数形结合即可得到方程f(x)=k,k∈[0,1)在[﹣1,5]的所有实根之和.
【解答】解:∵对任意的x∈R,都有f(2+x)=﹣f(x),
∴f(4+x)=f(x),
故f(x)是周期为4的周期函数.
∵函数f(x)是偶函数,
∴当x∈[﹣1,0]时,f(x)=﹣x2+1,
即x∈[﹣1,1]时,f(x)=﹣x2+1,对称轴为x=0,
当1≤x≤3时,﹣1≤x﹣2≤1,
∵f(2+x)=﹣f(x),
∴f(x)=﹣f(x﹣2),
此时f(x)=﹣f(x﹣2)=﹣[﹣(x﹣2)2+1]=(x﹣2)2﹣1.当3≤x≤5时,﹣1≤x﹣4≤1,
此时f(x)=f(x﹣4)=﹣(x﹣4)2+1.
作出函数f(x)在[﹣1,5]的图象如图:
由图象可知当1≤x≤3时,对称轴为x=2,
当3≤x≤5时,对称轴为x=4,
则当k∈[0,1),函数f(x)与y=k,有4个交点,
它们分别关于x=0,x=4对称,
设对称的交点的横坐标分别为x1,x2,x5,x6,
则x1+x2=0,x5+x6=2×4=8,
∴方程f(x)=k,k∈[0,1)在[﹣1,5]的所有实根之和为0+8=8,
故选:D.
12.(5分)设函数f'(x)是定义在(0,π)上的函数f(x)的导函数,有f'(x)cosx﹣f(x)sinx>0,若,,则a,b,c的大小关系是( )
A.a<b<c B.b<c<a C.c<b<a D.c<a<b
【分析】根据题意,构造新函数g(x)=f(x)cosx,求出其导数以及符号,分析可得g(x)在(0,π)上为增函数,又由=cosf()=g(),b=0=cosf()=g(),c=﹣f()=cosf()=g(),结合函数的单调性分析可得答案.
【解答】解:根据题意,设g(x)=f(x)cosx,
则g′(x)=f′(x)cosx+f(x)(cosx)′=f'(x)cosx﹣f(x)sinx,
又由f'(x)cosx﹣f(x)sinx>0,
则g′(x)>0,函数g(x)在(0,π)上为增函数,
=cosf()=g(),
b=0=cosf()=g(),c=﹣f()=cosf()=g(),
则有a<b<c;
故选:A.
二、填空题(本大题共4小题,共20分)
13.(5分)已知f(x+1)是定义域为R的偶函数,对于任意x1,x2∈(﹣∞,1]且x1≠x2,都有,且f(3)=0,则的解集为 (﹣∞,﹣1) (0,3) .
【分析】根据条件得到函数f(x)关于x=1对称,且当x≤1时,函数为增函数,则当x≥1时为减函数,结合函数单调性和对称性的关系,求解即可.
【解答】解:∵f(x+1)是定义域为R的偶函数,
∴f(﹣x+1)=f(x+1),即f(x)关于x=1对称,
∵对于任意x1,x2∈(﹣∞,1]且x1≠x2,都有,
∴当x≤1时,函数为增函数,则当x≥1时为减函数,
∵f(3)=0,∴f(﹣1)=f(3)=0,
作出函数f(x)的图象如图:
则等价为或,
∴0<x<3或x<﹣1,
即不等式的解集为(﹣∞,﹣1) (0,3),
故答案为:(﹣∞,﹣1) (0,3).
14.(5分)已知F为抛物线C:y2=x的焦点,点A,B在抛物线上,且分别位于x轴的上、下两侧,若△BFO的面积是(O为坐标原点),且=12,则直线AB的斜率是 ﹣ .
【分析】设直线AB的方程为:x=ty+m,点A(x1,y1),B(x2,y2),代入抛物线方程,运用韦达定理和三角形的面积,计算可得所求值.
【解答】解:设直线AB的方程为:x=ty+m,
点A(x1,y1),B(x2,y2),
x=ty+m代入y2=x,可得y2﹣ty﹣m=0,
根据韦达定理有y1 y2=﹣m,
∵=12,∴x1 x2+y1 y2=12,从而(y1 y2)2+y1 y2﹣12=0,
∵点A,B位于x轴的两侧,
∴y1 y2=﹣4,故m=4.
不妨令点A在x轴上方,则y1>0,
又F(,0),△BFO的面积是,可得×(﹣y2)=,
即有y1=1,y2=﹣4,x1=1,x2=16,
直线AB的斜率是:.
故答案为:.
15.(5分)在长方体ABCD﹣A1B1C1D1中,AB=1,AD=2,AA1=1,E为BC的中点,则点A到平面A1DE的距离是 .
【分析】利用等体积法,转化求解点A到平面A1DE的距离即可.
【解答】解:,,解得.
故答案为:.
16.(5分)已知F为双曲线的左焦点,过点F作直线l与圆x2+y2=a2相切于点A,且与双曲线右支相交于点B,若,则双曲线的离心率为 .
【分析】在△AFO中计算AF,cos∠AFO,利用余弦定理计算BF′,根据双曲线的定义得出BF′,列方程得出a,b,c的关系,从而可求出双曲线的离心率.
【解答】解:设双曲线的右焦点为F′,
∵OA=a,AF⊥OA,OF=c,
∴AF==b,∴cos∠AFO=,
∵,O是FF′的中点,
∴BF=3b,FF′=2c,
由双曲线的定义可知BF﹣BF′=2a,∴BF′=3b﹣2a,
在△BFF′中,由余弦定理可得BF′2=9b2+4c2﹣2=4c2﹣3b2,
∴(3b﹣2a)2=4c2﹣3b2,整理可得=,
∴e===.
故答案为:.
三、解答题:(本大题共6小题,17题10分,其余各12分,共70分)。
17.(10分)如下的三个图中,左面的是一个长方体截去一个角所得多面体的直观图,它的主视图和左视图在右面画出(单位:cm).(1)按照给出的尺寸,求该多面体的体积;(2)在所给直观图中连结BC′,证明:BC′∥面EFG.
【分析】(1)按照给出的尺寸,利用切割法得V=V长方体﹣V正三棱锥,代入体积公式求该多面体的体积;
(2)在长方体ABCD﹣A′B′C′D′中,连接AD′,根据条件和长方体的几何特征证明EG∥BC′,再由线面平行的判定定理证明BC′∥面EFG.
【解答】解:(1)由题意可得:
所求多面体体积V=V长方体﹣V正三棱锥
=4×4×6﹣××2×2×2=(cm2),
(2)证明:如图,
由多面体的左视图可得:点G、F分别是正方形的中点,
在长方体ABCD﹣A′B′C′D′中,连接AD′,
则AD′∥BC′
∵E,G分别为AA′,A′D′中点,
∴AD′∥EG,从而EG∥BC′,
又∵EG 平面EFG,BC′ 平面EFG,
∴BC′∥平面EFG.
18.(12分)已知函数f(x)=Asin(ωx+φ),其中A>0,ω>0,﹣<φ<,x∈R,其部分图象如图所示.
(1)求函数y=f(x)的解析式;
(2)已知函数g(x)=f(x)cosx,求函数g(x)的单调递增区间.
【分析】(1)直接利用函数的图象求出函数的关系式;
(2)利用三角恒等变换化简g(x),再利用正弦型函数的性质即可求出结果.
【解答】解:(1)由函数y=f(x)的图象可知,A=2,
=﹣=,故T=2π,所以ω=1,
又当x=时,sin(+φ)=1,且,﹣<φ<,故φ=,
所以f(x)=2sin(x+).
(2)g(x)=f(x)cosx=2sin(x+)cosx=2(sinx+cosx)cosx
=sinxcosx+cos2x=sin2x+cos2x+
=sin(2x+)+,
令﹣+2kπ≤2x+≤+2kπ,k∈Z,解得﹣+kπ≤x≤+kπ,k∈Z,
故g(x)的单调递增区间为[﹣+kπ,+kπ],k∈Z.
19.(12分)等差数列{an}中,a2=4,a4+a7=15.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=+n,求b1+b2+b3+…+b10的值.
【分析】(Ⅰ)建立方程组求出首项与公差,即可求数列{an}的通项公式;
(Ⅱ)bn=+n=2n+n,利用分组求和求b1+b2+b3+…+b10的值.
【解答】解:(Ⅰ)设公差为d,则,
解得,
所以an=3+(n﹣1)=n+2;
(Ⅱ)bn=+n=2n+n,
所以b1+b2+b3+…+b10=(2+1)+(22+2)+…+(210+10)
=(2+22+…+210)+(1+2+…+10)
=+=2101.
20.(12分)在△ABC中,a,b,c分别是角A,B,C的对边,已知(sinA+sinB)2﹣sin2C=3sinAsinB.
(1)求角C;
(2)若b=4,且△ABC为锐角三角形,求△ABC面积的取值范围.
【分析】(1)利用正弦定理将已知等式中的角化边,再结合余弦定理,即可得解;
(2)结合C=和锐角△ABC,可推出B的取值范围,再由正弦定理可得c=,最后根据S=bcsinA、正弦的两角差公式和正切函数的性质,得解.
【解答】解:(1)由正弦定理知,==,
因为(sinA+sinB)2﹣sin2C=3sinAsinB,
所以(a+b)2﹣c2=3ab,化简得a2+b2﹣c2=ab,
由余弦定理知,cosC===,
因为C∈(0,π),所以C=.
(2)由(1)知,C=,
所以A+B=,
又△ABC是锐角三角形,
所以,解得<B<,
由正弦定理知,=,所以c=,
△ABC面积S=bcsinA=×4××sin(﹣B)
=4×
==+2,
因为<B<,所以tanB>,
所以2<S<8,
故△ABC面积的取值范围为(2,8).
21.(12分)设函数f(x)=(a,b>0).
(1)若函数f(x)在x=1处的切线方程是bx+4y﹣3=0,求实数a,b的值;
(2)在(1)的条件下,若2(x﹣k)f(x)≥lnx对于0<x≤1恒成立,求实数k的取值范围.
【分析】(1)求出函数的导数,计算f(1),f′(1),求出切线方程,根据对应关系求出a,b的值即可;
(2)问题转化为k≤x﹣(x+1)lnx,令g(x)=x﹣(x+1)lnx,根据函数的单调性求出k的范围即可.
【解答】解:(1)∵f′(x)=﹣,∴f′(1)=﹣,
∴f(x)在x=1处的切线方程是y﹣=﹣(x﹣1),
由题意得,解得:或,
∵a,b>0,∴a=b=1;
(2)∵2(x﹣k)f(x)≥lnx,∴k≤x﹣(x+1)lnx,
令g(x)=x﹣(x+1)lnx,则g′(x)=(1﹣lnx﹣),
令h(x)=g′(x)=(1﹣lnx﹣),∴h′(x)=(﹣+)=,
当x∈(0,1]时,h′(x)≥0,h(x)递增,即g′(x)递增,
∴g′(x)≤(1﹣ln1﹣1)=0,故g(x)在(0,1]递减,
故g(x)min=g(1)=1,
故实数k的取值范围是(﹣∞,1].
22.(12分)已知数列{an}是首项为正数的等差数列,数列{}的前n项和为.
(1)求数列{an}的通项公式;
(2)设bn=(an+1) 2an,求数列{bn}的前n项和Tn.
【分析】(1)利用等差数列的通项公式即可得出.
(2)由(1)可得bn=8n2﹣4n,分组求和即可
【解答】解:(1)设数列{an}的公差为d,
令n=1,得=,所以a1a2=3.
令n=2,得+=,所以a2a3=15.
解得a1=1,d=2,
∴an=2n﹣1,
(2)bn=(an+1) 2an=(2n+1﹣1)×2×(2n﹣1)=8n2﹣4n
∴Tn=b1+b2+…+bn,
=8(12+22+32+…+n2)﹣4(1+2+3+…+n),
=8×﹣4×
=
一、选择题(本大题共12小题,每小题5分,共60分)
1.(5分)设a,b∈R,集合{1,a+b,a}={0,,b},则b﹣a=( )
A.1 B.﹣1 C.2 D.﹣2
2.(5分)集合A={x|y=},B={y|y=2x,x>0},则A∩B=( )
A.[0,2] B.(1,2] C.[1,2] D.(1,+∞)
3.(5分)已知﹣<α<0,sinα+cosα=,则的值为( )
A. B. C. D.
4.(5分)在某种新型材料的研制中,实验人员获得了下列一组实验数据:现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是( )
x 1.992 3 4 5.15 6.126
y 1.517 4.0418 7.5 12 18.01
A.y=2x﹣2 B.y=(x2﹣1) C.y=log2x D.y=x
5.(5分)已知函数f(x)=,若互不相等的实数x1,x2,x3满足f(x1)=f(x2)=f(x3),则x1+x2+x3的取值范围为( )
A.() B.(﹣,) C.(,6] D.(﹣,]
6.(5分)函数f(x)=sin(2x+)向右平移φ(0≤φ≤π)个单位后得到函数g(x),若g(x)在(﹣,)上单调递增,则φ的取值范围是( )
A.[0,] B.[0,] C.[,] D.[,]
7.(5分)某几何体的三视图如图所示,则该几何体的外接球的球面面积为( )
A.5π B.12π C.20π D.8π
8.(5分)已知函数f(x)是定义在R上的偶函数,且在(﹣∞,0)上单调递减,若,b=f(log24.1),c=f(20.8),则a,b,c的大小关系是( )
A.a<b<c B.b<a<c C.c<a<b D.c<b<a
9.(5分)下列选项叙述错误的是( )
A.命题“若x≠1,则x2﹣3x+2≠0”的逆否命题是“若x2﹣3x+2=0,则x=1”
B.若命题p:x∈A∩B,则命题¬p是x A或x B
C.若p∨q为真命题,则p,q均为真命题
D.“x>2”是“x2﹣3x+2>0”的充分不必要条件
10.(5分)函数y=loga(x+3)﹣1(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny+2=0上(其中m,n>0),则的最小值等于( )
A.10 B.8 C.6 D.4
11.(5分)已知f(x)是定义在R上的偶函数,对任意的x∈R,都有f(2+x)=﹣f(x),且当x∈[0,1]时f(x)=﹣x2+1,则方程f(x)=k,k∈[0,1)在[﹣1,5]的所有实根之和为( )
A.0 B.2 C.4 D.8
12.(5分)设函数f'(x)是定义在(0,π)上的函数f(x)的导函数,有f'(x)cosx﹣f(x)sinx>0,若,,则a,b,c的大小关系是( )
A.a<b<c B.b<c<a C.c<b<a D.c<a<b
二、填空题(本大题共4小题,共20分)
13.(5分)已知f(x+1)是定义域为R的偶函数,对于任意x1,x2∈(﹣∞,1]且x1≠x2,都有,且f(3)=0,则的解集为 .
14.(5分)已知F为抛物线C:y2=x的焦点,点A,B在抛物线上,且分别位于x轴的上、下两侧,若△BFO的面积是(O为坐标原点),且=12,则直线AB的斜率是 .
15.(5分)在长方体ABCD﹣A1B1C1D1中,AB=1,AD=2,AA1=1,E为BC的中点,则点A到平面A1DE的距离是 .
16.(5分)已知F为双曲线的左焦点,过点F作直线l与圆x2+y2=a2相切于点A,且与双曲线右支相交于点B,若,则双曲线的离心率为 .
三、解答题:(本大题共6小题,17题10分,其余各12分,共70分)。
17.(10分)如下的三个图中,左面的是一个长方体截去一个角所得多面体的直观图,它的主视图和左视图在右面画出(单位:cm).(1)按照给出的尺寸,求该多面体的体积;(2)在所给直观图中连结BC′,证明:BC′∥面EFG.
18.(12分)已知函数f(x)=Asin(ωx+φ),其中A>0,ω>0,﹣<φ<,x∈R,其部分图象如图所示.
(1)求函数y=f(x)的解析式;
(2)已知函数g(x)=f(x)cosx,求函数g(x)的单调递增区间.
19.(12分)等差数列{an}中,a2=4,a4+a7=15.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=+n,求b1+b2+b3+…+b10的值.
20.(12分)在△ABC中,a,b,c分别是角A,B,C的对边,已知(sinA+sinB)2﹣sin2C=3sinAsinB.
(1)求角C;
(2)若b=4,且△ABC为锐角三角形,求△ABC面积的取值范围.
21.(12分)设函数f(x)=(a,b>0).
(1)若函数f(x)在x=1处的切线方程是bx+4y﹣3=0,求实数a,b的值;
(2)在(1)的条件下,若2(x﹣k)f(x)≥lnx对于0<x≤1恒成立,求实数k的取值范围.
22.(12分)已知数列{an}是首项为正数的等差数列,数列{}的前n项和为.
(1)求数列{an}的通项公式;
(2)设bn=(an+1) 2an,求数列{bn}的前n项和Tn.
2021-2022学年河南省焦作市县级重点中学高三(上)期中联考
数学试卷(文科)
参考答案与试题解析
一、选择题(本大题共12小题,每小题5分,共60分)
1.(5分)设a,b∈R,集合{1,a+b,a}={0,,b},则b﹣a=( )
A.1 B.﹣1 C.2 D.﹣2
【分析】根据题意,集合,注意到后面集合中有元素0,由集合相等的意义,结合集合中元素的特征,可得a+b=0,进而分析可得a、b的值,计算可得答案.
【解答】解:根据题意,集合,
又∵a≠0,
∴a+b=0,即a=﹣b,
∴,
b=1;
故a=﹣1,b=1,
则b﹣a=2,
故选:C.
2.(5分)集合A={x|y=},B={y|y=2x,x>0},则A∩B=( )
A.[0,2] B.(1,2] C.[1,2] D.(1,+∞)
【分析】先分别求出集合A,B,由此能求出A∩B.
【解答】解:∵集合={x|0≤x≤2}.
B={y|y=2x,x>0}={y|y>1},
∴A∩B={x|1<x≤2}=(1,2].
故选:B.
3.(5分)已知﹣<α<0,sinα+cosα=,则的值为( )
A. B. C. D.
【分析】先求出sin2α,再求出cos2α,即可求出的值.
【解答】解:∵sinα+cosα=,
∴1+2sinαcosα=,
∴sin2α=﹣,
∵﹣<α<0,sinα+cosα=,
∴﹣π<2α<0,|sinα|<|cosα|,
∴cos2α=,
∴==,
故选:C.
4.(5分)在某种新型材料的研制中,实验人员获得了下列一组实验数据:现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是( )
x 1.992 3 4 5.15 6.126
y 1.517 4.0418 7.5 12 18.01
A.y=2x﹣2 B.y=(x2﹣1) C.y=log2x D.y=x
【分析】由表中的数据分析得出,自变量基本上是等速增加,相应的函数值增加的速度越来越快,结合基本初等函数的图象与性质,利用排除法即可得出正确的答案.
【解答】解:由题意得,表中数据y随x的变化趋势,函数在(0,+∞)上是增函数,
且y的变化随x的增大越来越快;
∵A中函数是线性增加的函数,C中函数是比线性增加还缓慢的函数,D中函数是减函数;
∴排除A,C、D答案;
∴B中函数y=(x2﹣1)符合题意.
故选:B.
5.(5分)已知函数f(x)=,若互不相等的实数x1,x2,x3满足f(x1)=f(x2)=f(x3),则x1+x2+x3的取值范围为( )
A.() B.(﹣,) C.(,6] D.(﹣,]
【分析】先作出函数f(x)=的图象,如图,不妨设x1<x2<x3,则x2,x3关于直线x=3对称,得到x2+x3=6,且﹣<x1<0;最后结合求得x1+x2+x3的取值范围即可.
【解答】解:函数f(x)=的图象,如图,
不妨设x1<x2<x3,则x2,x3关于直线x=3对称,故x2+x3=6,
且x1满足﹣<x1<0;
则x1+x2+x3的取值范围是:﹣+6<x1+x2+x3<0+6;
即x1+x2+x3∈(,6).
故选:A.
6.(5分)函数f(x)=sin(2x+)向右平移φ(0≤φ≤π)个单位后得到函数g(x),若g(x)在(﹣,)上单调递增,则φ的取值范围是( )
A.[0,] B.[0,] C.[,] D.[,]
【分析】利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再利用正弦函数的单调性,求得φ的取值范围.
【解答】解:把函数f(x)=sin(2x+)向右平移φ(0≤φ≤π)个单位后得到函数g(x)=sin(2x﹣2φ+)的图象,
若g(x)在(﹣,)上单调递增,则﹣﹣2φ+≥﹣,且 ﹣2φ+≤,
求得≤φ≤,
故选:D.
7.(5分)某几何体的三视图如图所示,则该几何体的外接球的球面面积为( )
A.5π B.12π C.20π D.8π
【分析】三视图复原的几何体是底面为长、宽分别为3,4的长方形,侧棱垂直于底面的四棱锥;把它扩展为长方体,它的外接球的直径就是长方体的对角线的长,求出对角线长,即可求出外接球的表面积.
【解答】解:三视图复原的几何体是底面为长、宽分别为3,4的长方形,侧棱垂直于底面的四棱锥;把它扩展为长方体,
则长、宽、高分别为1,1,,
则它的外接球的直径就是长方体的对角线的长,
所以长方体的对角线长为:=
所以球的半径为:R=.
这个几何体的外接球的表面积是:4πR2=5π.
故选:A.
8.(5分)已知函数f(x)是定义在R上的偶函数,且在(﹣∞,0)上单调递减,若,b=f(log24.1),c=f(20.8),则a,b,c的大小关系是( )
A.a<b<c B.b<a<c C.c<a<b D.c<b<a
【分析】由奇偶性将数转化为(0,+∞)上,然后根据单调性比较大小.
【解答】解:由于f(x)为偶函数,则=f(﹣log25)=f(log25),
∵,函数f(x)是定义在R上的偶函数,且在(﹣∞,0)上单调递减
∴函数f(x)在(0,+∞)上单调递增,
∴>b=f(log24.1)>c=f(20.8),
故选:D.
9.(5分)下列选项叙述错误的是( )
A.命题“若x≠1,则x2﹣3x+2≠0”的逆否命题是“若x2﹣3x+2=0,则x=1”
B.若命题p:x∈A∩B,则命题¬p是x A或x B
C.若p∨q为真命题,则p,q均为真命题
D.“x>2”是“x2﹣3x+2>0”的充分不必要条件
【分析】利用逆否命题判断A的正误;命题的否定判断B的正误;或命题的真假判断C的正误;充要条件判断D的正误;
【解答】解:对于A,命题“若x≠1,则x2﹣3x+2≠0”的逆否命题是“若x2﹣3x+2=0,则x=1”,满足逆否命题的形式,所以A正确;
对于B,若命题p:x∈A∩B,则命题¬p是x A或x B,满足命题的否定的形式,所以B正确;
对于C,若p∨q为真命题,则p,q一真即可,说p,q均为真命题,不正确,所以C不正确;
对于D,“x>2”是“x2﹣3x+2>0”的充分不必要条件,前者能够说明后者,后者推不出前者,所以D正确;
故选:C.
10.(5分)函数y=loga(x+3)﹣1(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny+2=0上(其中m,n>0),则的最小值等于( )
A.10 B.8 C.6 D.4
【分析】先求出定点A的坐标,再把A代入直线方程,利用基本不等式求得的最小值.
【解答】解:令x+3=1,求得x=﹣2,可得函数y=loga(x+3)﹣1(a>0,且a≠1)的图象恒过定点A(﹣2,﹣1),
若点A在直线mx+ny+2=0上(其中m,n>0),则﹣2m﹣n+2=0,即 2m+n=2.
由基本不等式可得2≥2,即mn≤,即≥2,当且仅当2m=n=1时,取等号.
则==≥4,
故选:D.
11.(5分)已知f(x)是定义在R上的偶函数,对任意的x∈R,都有f(2+x)=﹣f(x),且当x∈[0,1]时f(x)=﹣x2+1,则方程f(x)=k,k∈[0,1)在[﹣1,5]的所有实根之和为( )
A.0 B.2 C.4 D.8
【分析】由f(x+2)=﹣f(x),可知f(x)是周期为4的周期函数.再由f(x)是偶函数,当x∈[0,1]时,f(x)=﹣x2+1,可得函数在[﹣1,5]上的解析式.利用数形结合即可得到方程f(x)=k,k∈[0,1)在[﹣1,5]的所有实根之和.
【解答】解:∵对任意的x∈R,都有f(2+x)=﹣f(x),
∴f(4+x)=f(x),
故f(x)是周期为4的周期函数.
∵函数f(x)是偶函数,
∴当x∈[﹣1,0]时,f(x)=﹣x2+1,
即x∈[﹣1,1]时,f(x)=﹣x2+1,对称轴为x=0,
当1≤x≤3时,﹣1≤x﹣2≤1,
∵f(2+x)=﹣f(x),
∴f(x)=﹣f(x﹣2),
此时f(x)=﹣f(x﹣2)=﹣[﹣(x﹣2)2+1]=(x﹣2)2﹣1.当3≤x≤5时,﹣1≤x﹣4≤1,
此时f(x)=f(x﹣4)=﹣(x﹣4)2+1.
作出函数f(x)在[﹣1,5]的图象如图:
由图象可知当1≤x≤3时,对称轴为x=2,
当3≤x≤5时,对称轴为x=4,
则当k∈[0,1),函数f(x)与y=k,有4个交点,
它们分别关于x=0,x=4对称,
设对称的交点的横坐标分别为x1,x2,x5,x6,
则x1+x2=0,x5+x6=2×4=8,
∴方程f(x)=k,k∈[0,1)在[﹣1,5]的所有实根之和为0+8=8,
故选:D.
12.(5分)设函数f'(x)是定义在(0,π)上的函数f(x)的导函数,有f'(x)cosx﹣f(x)sinx>0,若,,则a,b,c的大小关系是( )
A.a<b<c B.b<c<a C.c<b<a D.c<a<b
【分析】根据题意,构造新函数g(x)=f(x)cosx,求出其导数以及符号,分析可得g(x)在(0,π)上为增函数,又由=cosf()=g(),b=0=cosf()=g(),c=﹣f()=cosf()=g(),结合函数的单调性分析可得答案.
【解答】解:根据题意,设g(x)=f(x)cosx,
则g′(x)=f′(x)cosx+f(x)(cosx)′=f'(x)cosx﹣f(x)sinx,
又由f'(x)cosx﹣f(x)sinx>0,
则g′(x)>0,函数g(x)在(0,π)上为增函数,
=cosf()=g(),
b=0=cosf()=g(),c=﹣f()=cosf()=g(),
则有a<b<c;
故选:A.
二、填空题(本大题共4小题,共20分)
13.(5分)已知f(x+1)是定义域为R的偶函数,对于任意x1,x2∈(﹣∞,1]且x1≠x2,都有,且f(3)=0,则的解集为 (﹣∞,﹣1) (0,3) .
【分析】根据条件得到函数f(x)关于x=1对称,且当x≤1时,函数为增函数,则当x≥1时为减函数,结合函数单调性和对称性的关系,求解即可.
【解答】解:∵f(x+1)是定义域为R的偶函数,
∴f(﹣x+1)=f(x+1),即f(x)关于x=1对称,
∵对于任意x1,x2∈(﹣∞,1]且x1≠x2,都有,
∴当x≤1时,函数为增函数,则当x≥1时为减函数,
∵f(3)=0,∴f(﹣1)=f(3)=0,
作出函数f(x)的图象如图:
则等价为或,
∴0<x<3或x<﹣1,
即不等式的解集为(﹣∞,﹣1) (0,3),
故答案为:(﹣∞,﹣1) (0,3).
14.(5分)已知F为抛物线C:y2=x的焦点,点A,B在抛物线上,且分别位于x轴的上、下两侧,若△BFO的面积是(O为坐标原点),且=12,则直线AB的斜率是 ﹣ .
【分析】设直线AB的方程为:x=ty+m,点A(x1,y1),B(x2,y2),代入抛物线方程,运用韦达定理和三角形的面积,计算可得所求值.
【解答】解:设直线AB的方程为:x=ty+m,
点A(x1,y1),B(x2,y2),
x=ty+m代入y2=x,可得y2﹣ty﹣m=0,
根据韦达定理有y1 y2=﹣m,
∵=12,∴x1 x2+y1 y2=12,从而(y1 y2)2+y1 y2﹣12=0,
∵点A,B位于x轴的两侧,
∴y1 y2=﹣4,故m=4.
不妨令点A在x轴上方,则y1>0,
又F(,0),△BFO的面积是,可得×(﹣y2)=,
即有y1=1,y2=﹣4,x1=1,x2=16,
直线AB的斜率是:.
故答案为:.
15.(5分)在长方体ABCD﹣A1B1C1D1中,AB=1,AD=2,AA1=1,E为BC的中点,则点A到平面A1DE的距离是 .
【分析】利用等体积法,转化求解点A到平面A1DE的距离即可.
【解答】解:,,解得.
故答案为:.
16.(5分)已知F为双曲线的左焦点,过点F作直线l与圆x2+y2=a2相切于点A,且与双曲线右支相交于点B,若,则双曲线的离心率为 .
【分析】在△AFO中计算AF,cos∠AFO,利用余弦定理计算BF′,根据双曲线的定义得出BF′,列方程得出a,b,c的关系,从而可求出双曲线的离心率.
【解答】解:设双曲线的右焦点为F′,
∵OA=a,AF⊥OA,OF=c,
∴AF==b,∴cos∠AFO=,
∵,O是FF′的中点,
∴BF=3b,FF′=2c,
由双曲线的定义可知BF﹣BF′=2a,∴BF′=3b﹣2a,
在△BFF′中,由余弦定理可得BF′2=9b2+4c2﹣2=4c2﹣3b2,
∴(3b﹣2a)2=4c2﹣3b2,整理可得=,
∴e===.
故答案为:.
三、解答题:(本大题共6小题,17题10分,其余各12分,共70分)。
17.(10分)如下的三个图中,左面的是一个长方体截去一个角所得多面体的直观图,它的主视图和左视图在右面画出(单位:cm).(1)按照给出的尺寸,求该多面体的体积;(2)在所给直观图中连结BC′,证明:BC′∥面EFG.
【分析】(1)按照给出的尺寸,利用切割法得V=V长方体﹣V正三棱锥,代入体积公式求该多面体的体积;
(2)在长方体ABCD﹣A′B′C′D′中,连接AD′,根据条件和长方体的几何特征证明EG∥BC′,再由线面平行的判定定理证明BC′∥面EFG.
【解答】解:(1)由题意可得:
所求多面体体积V=V长方体﹣V正三棱锥
=4×4×6﹣××2×2×2=(cm2),
(2)证明:如图,
由多面体的左视图可得:点G、F分别是正方形的中点,
在长方体ABCD﹣A′B′C′D′中,连接AD′,
则AD′∥BC′
∵E,G分别为AA′,A′D′中点,
∴AD′∥EG,从而EG∥BC′,
又∵EG 平面EFG,BC′ 平面EFG,
∴BC′∥平面EFG.
18.(12分)已知函数f(x)=Asin(ωx+φ),其中A>0,ω>0,﹣<φ<,x∈R,其部分图象如图所示.
(1)求函数y=f(x)的解析式;
(2)已知函数g(x)=f(x)cosx,求函数g(x)的单调递增区间.
【分析】(1)直接利用函数的图象求出函数的关系式;
(2)利用三角恒等变换化简g(x),再利用正弦型函数的性质即可求出结果.
【解答】解:(1)由函数y=f(x)的图象可知,A=2,
=﹣=,故T=2π,所以ω=1,
又当x=时,sin(+φ)=1,且,﹣<φ<,故φ=,
所以f(x)=2sin(x+).
(2)g(x)=f(x)cosx=2sin(x+)cosx=2(sinx+cosx)cosx
=sinxcosx+cos2x=sin2x+cos2x+
=sin(2x+)+,
令﹣+2kπ≤2x+≤+2kπ,k∈Z,解得﹣+kπ≤x≤+kπ,k∈Z,
故g(x)的单调递增区间为[﹣+kπ,+kπ],k∈Z.
19.(12分)等差数列{an}中,a2=4,a4+a7=15.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=+n,求b1+b2+b3+…+b10的值.
【分析】(Ⅰ)建立方程组求出首项与公差,即可求数列{an}的通项公式;
(Ⅱ)bn=+n=2n+n,利用分组求和求b1+b2+b3+…+b10的值.
【解答】解:(Ⅰ)设公差为d,则,
解得,
所以an=3+(n﹣1)=n+2;
(Ⅱ)bn=+n=2n+n,
所以b1+b2+b3+…+b10=(2+1)+(22+2)+…+(210+10)
=(2+22+…+210)+(1+2+…+10)
=+=2101.
20.(12分)在△ABC中,a,b,c分别是角A,B,C的对边,已知(sinA+sinB)2﹣sin2C=3sinAsinB.
(1)求角C;
(2)若b=4,且△ABC为锐角三角形,求△ABC面积的取值范围.
【分析】(1)利用正弦定理将已知等式中的角化边,再结合余弦定理,即可得解;
(2)结合C=和锐角△ABC,可推出B的取值范围,再由正弦定理可得c=,最后根据S=bcsinA、正弦的两角差公式和正切函数的性质,得解.
【解答】解:(1)由正弦定理知,==,
因为(sinA+sinB)2﹣sin2C=3sinAsinB,
所以(a+b)2﹣c2=3ab,化简得a2+b2﹣c2=ab,
由余弦定理知,cosC===,
因为C∈(0,π),所以C=.
(2)由(1)知,C=,
所以A+B=,
又△ABC是锐角三角形,
所以,解得<B<,
由正弦定理知,=,所以c=,
△ABC面积S=bcsinA=×4××sin(﹣B)
=4×
==+2,
因为<B<,所以tanB>,
所以2<S<8,
故△ABC面积的取值范围为(2,8).
21.(12分)设函数f(x)=(a,b>0).
(1)若函数f(x)在x=1处的切线方程是bx+4y﹣3=0,求实数a,b的值;
(2)在(1)的条件下,若2(x﹣k)f(x)≥lnx对于0<x≤1恒成立,求实数k的取值范围.
【分析】(1)求出函数的导数,计算f(1),f′(1),求出切线方程,根据对应关系求出a,b的值即可;
(2)问题转化为k≤x﹣(x+1)lnx,令g(x)=x﹣(x+1)lnx,根据函数的单调性求出k的范围即可.
【解答】解:(1)∵f′(x)=﹣,∴f′(1)=﹣,
∴f(x)在x=1处的切线方程是y﹣=﹣(x﹣1),
由题意得,解得:或,
∵a,b>0,∴a=b=1;
(2)∵2(x﹣k)f(x)≥lnx,∴k≤x﹣(x+1)lnx,
令g(x)=x﹣(x+1)lnx,则g′(x)=(1﹣lnx﹣),
令h(x)=g′(x)=(1﹣lnx﹣),∴h′(x)=(﹣+)=,
当x∈(0,1]时,h′(x)≥0,h(x)递增,即g′(x)递增,
∴g′(x)≤(1﹣ln1﹣1)=0,故g(x)在(0,1]递减,
故g(x)min=g(1)=1,
故实数k的取值范围是(﹣∞,1].
22.(12分)已知数列{an}是首项为正数的等差数列,数列{}的前n项和为.
(1)求数列{an}的通项公式;
(2)设bn=(an+1) 2an,求数列{bn}的前n项和Tn.
【分析】(1)利用等差数列的通项公式即可得出.
(2)由(1)可得bn=8n2﹣4n,分组求和即可
【解答】解:(1)设数列{an}的公差为d,
令n=1,得=,所以a1a2=3.
令n=2,得+=,所以a2a3=15.
解得a1=1,d=2,
∴an=2n﹣1,
(2)bn=(an+1) 2an=(2n+1﹣1)×2×(2n﹣1)=8n2﹣4n
∴Tn=b1+b2+…+bn,
=8(12+22+32+…+n2)﹣4(1+2+3+…+n),
=8×﹣4×
=
同课章节目录
