人教版 六年级数学上册5.5解决生活中圆的问题(课件共18张PPT)
文档属性
| 名称 | 人教版 六年级数学上册5.5解决生活中圆的问题(课件共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-14 20:33:22 | ||
图片预览





文档简介
(共18张PPT)
解决生活中圆的问题
使学生能正确运用圆的有关知识,解决简单的实际问题。
使学生进一步体会运用已有知识解决新问题的乐趣,发展空间观念和初步的推理能力。
了解现实生活中有许多与圆的面积有关的问题,获得运用知识解决问题的成功体验。
你从中读出哪些数学信息?
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计,图中的两个圆半径都是1米,你能求出正方形和圆之间的面积吗?
新课导入
课前活动一:
讨论交流:
观看微课《解决生活中圆的问题》,举例说说解决生活中圆的问题的方法,归纳总结后,交流互评。
课前活动
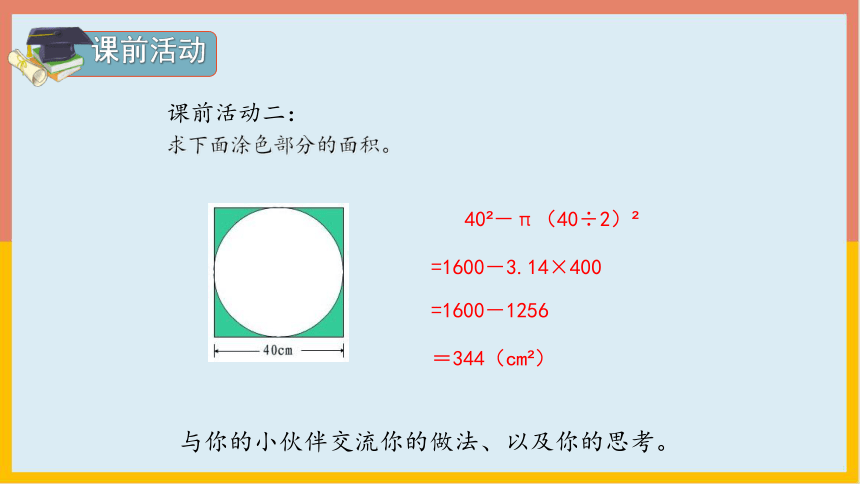
课前活动二:
求下面涂色部分的面积。
40 -π(40÷2)
=1600-3.14×400
=344(cm )
课前活动
与你的小伙伴交流你的做法、以及你的思考。
=1600-1256
探究一:
两个圆的半径都是1米。
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计,图中的两个圆半径都是1米,你能求出正方形和圆之间的面积吗?
左图求的是正方形比圆多的面积,
右图求的是圆比正方形多的面积。
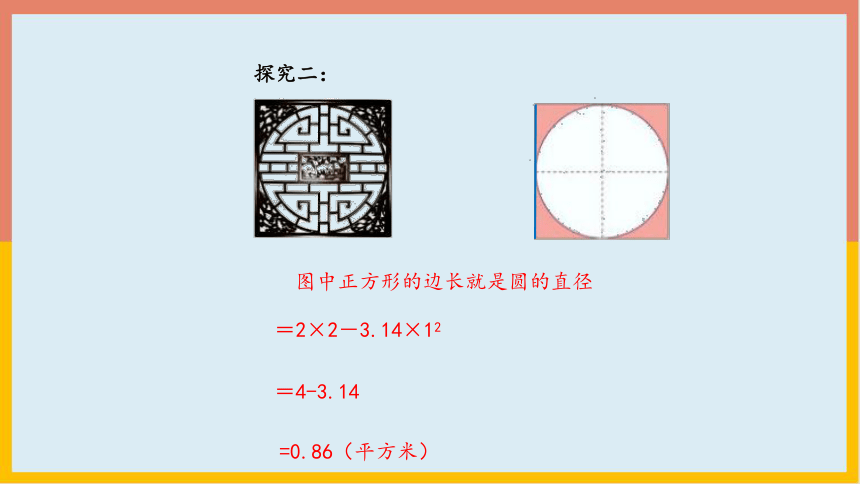
探究二:
图中正方形的边长就是圆的直径
=2×2-3.14×12
=4-3.14
=0.86(平方米)
探究二:
可以把正方形看成两个三角形,它的底是圆的直径,高是圆的半径。
=3.14×12-(2×1÷2)×2
=3.14-2
=1.14(平方米)
探究三:
左图:(2r)2-3.14×r2=0.86r2
如果两个圆的半径都是r,结果又是怎样的?
右图:3.14×r2-(2r×r÷2)×2=1.14r2
当r=1米时,和前面的结果是完全一样的。
答:左图中正方形与圆之间的面积是0.86平方米。
右图中圆与正方形之间的面积是1.14平方米。
1.14r2
答:外面的圆与内部的正方形之间的面积是164.16cm 。
图中是一面我国唐代外圆内方的铜镜。铜镜的直径是24厘米,外面的圆与内部的正方形之间的面积是多少?
=1.14×(24÷2)
=164.16(cm )
练一练
1.右图中的铜钱直径28毫米,中间的正方形边长为6毫米。这个铜钱的面积是多少?
答:这个铜钱的面积是579.44mm 。
3.14×(28÷2) -6
=615.44-36
=579.44(mm )
2.图中的大圆的半径等于小圆的直径,请你求出阴影部分的面积。
答:阴影部分的面积是84.78cm 。
3.14×【6 -(6÷2) 】
=3.14×27
=84.78(cm )
3.一个运动场如右图,两端是半圆形,中间是长方形,这个运动场的周长是多少米?面积是多少米?
周长:100×2+3.14×32×2
=200+200.96
=400.96(m)
答:这个运动场的周长是400.96m。
面积:100×(32×2)+3.14×322
=6400+3215.36
=9615.36(m2)
3.一个运动场如右图,两端是半圆形,中间是长方形,这个运动场的周长是多少米?面积是多少米?
答:这个运动场的面积是9615.36m2。
4.一个圆的周长是62.8米,半径增加了2米后,面积增加了多少平方米?
=138.16(m )
62.8÷3.14÷2=10(米)
3.14×(10+2)2-3.14×102
=452.16-314
答:面积增加了138.16m2。
1.外方内圆的两个图形的面积差为:0.86r2。
2.外圆内方的两个图形的面积差为:1.14r2。
3.求不规则的图形的面积可以根据实际情况来解答。
解决生活中圆的问题
课堂小结
1.完成《解决生活中圆的问题课后作业》;
2.讨论交流:
观看微课《扇形、圆心角和弧》,举例说说你对扇形的认识,归纳总结后,交流互评。
作业布置
再见
解决生活中圆的问题
使学生能正确运用圆的有关知识,解决简单的实际问题。
使学生进一步体会运用已有知识解决新问题的乐趣,发展空间观念和初步的推理能力。
了解现实生活中有许多与圆的面积有关的问题,获得运用知识解决问题的成功体验。
你从中读出哪些数学信息?
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计,图中的两个圆半径都是1米,你能求出正方形和圆之间的面积吗?
新课导入
课前活动一:
讨论交流:
观看微课《解决生活中圆的问题》,举例说说解决生活中圆的问题的方法,归纳总结后,交流互评。
课前活动
课前活动二:
求下面涂色部分的面积。
40 -π(40÷2)
=1600-3.14×400
=344(cm )
课前活动
与你的小伙伴交流你的做法、以及你的思考。
=1600-1256
探究一:
两个圆的半径都是1米。
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计,图中的两个圆半径都是1米,你能求出正方形和圆之间的面积吗?
左图求的是正方形比圆多的面积,
右图求的是圆比正方形多的面积。
探究二:
图中正方形的边长就是圆的直径
=2×2-3.14×12
=4-3.14
=0.86(平方米)
探究二:
可以把正方形看成两个三角形,它的底是圆的直径,高是圆的半径。
=3.14×12-(2×1÷2)×2
=3.14-2
=1.14(平方米)
探究三:
左图:(2r)2-3.14×r2=0.86r2
如果两个圆的半径都是r,结果又是怎样的?
右图:3.14×r2-(2r×r÷2)×2=1.14r2
当r=1米时,和前面的结果是完全一样的。
答:左图中正方形与圆之间的面积是0.86平方米。
右图中圆与正方形之间的面积是1.14平方米。
1.14r2
答:外面的圆与内部的正方形之间的面积是164.16cm 。
图中是一面我国唐代外圆内方的铜镜。铜镜的直径是24厘米,外面的圆与内部的正方形之间的面积是多少?
=1.14×(24÷2)
=164.16(cm )
练一练
1.右图中的铜钱直径28毫米,中间的正方形边长为6毫米。这个铜钱的面积是多少?
答:这个铜钱的面积是579.44mm 。
3.14×(28÷2) -6
=615.44-36
=579.44(mm )
2.图中的大圆的半径等于小圆的直径,请你求出阴影部分的面积。
答:阴影部分的面积是84.78cm 。
3.14×【6 -(6÷2) 】
=3.14×27
=84.78(cm )
3.一个运动场如右图,两端是半圆形,中间是长方形,这个运动场的周长是多少米?面积是多少米?
周长:100×2+3.14×32×2
=200+200.96
=400.96(m)
答:这个运动场的周长是400.96m。
面积:100×(32×2)+3.14×322
=6400+3215.36
=9615.36(m2)
3.一个运动场如右图,两端是半圆形,中间是长方形,这个运动场的周长是多少米?面积是多少米?
答:这个运动场的面积是9615.36m2。
4.一个圆的周长是62.8米,半径增加了2米后,面积增加了多少平方米?
=138.16(m )
62.8÷3.14÷2=10(米)
3.14×(10+2)2-3.14×102
=452.16-314
答:面积增加了138.16m2。
1.外方内圆的两个图形的面积差为:0.86r2。
2.外圆内方的两个图形的面积差为:1.14r2。
3.求不规则的图形的面积可以根据实际情况来解答。
解决生活中圆的问题
课堂小结
1.完成《解决生活中圆的问题课后作业》;
2.讨论交流:
观看微课《扇形、圆心角和弧》,举例说说你对扇形的认识,归纳总结后,交流互评。
作业布置
再见
