北师大版数学九年级上册4.7相似三角形的性质(一)课件(共19张PPT)
文档属性
| 名称 | 北师大版数学九年级上册4.7相似三角形的性质(一)课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 417.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 15:54:36 | ||
图片预览






文档简介
(共19张PPT)
4.7相似三角形的性质(一)
北师大版九上第四章《图形的相似》
还记得相似三角形的定义吗 还记得相似多边形的对应边、对应角有什么关系吗?
在两个相似三角形中是否只有对应角相等、对应边成比例这个性质呢?本节课我们将研究相似三角形的其他性质.
【回顾与反思】
相似三角形的对应边成比例、对应角相等。
学习目标:
经历探索相似三角形中对应线段比值与相似比的关系的过程,理解相似三角形的性质。
利用相似三角形的性质解决一些实际问题.
1、相似三角形有哪些判别方法?
2、相似三角形有什么性质?
相似三角形的的判别方法:
(1)两角分别相等的两个三角形相似
(2)两边成比例且夹角相等的两个三角形相似
(3)三边成比例的两个三角形相似
相似三角形的性质:
相似三角形的对应角相等,对应边成比例。
【复习引入】
3、如图,△ABC∽△A′B′C′。
(1)△ABC与△A′B′C′的相似比为 。
(2)请说出△ABC与△A′B′C′各角的关系,
各边的关系。
【复习引入】
2︰3
角:∠A=∠A′ ∠B=∠B′ ∠C=∠C′
边:
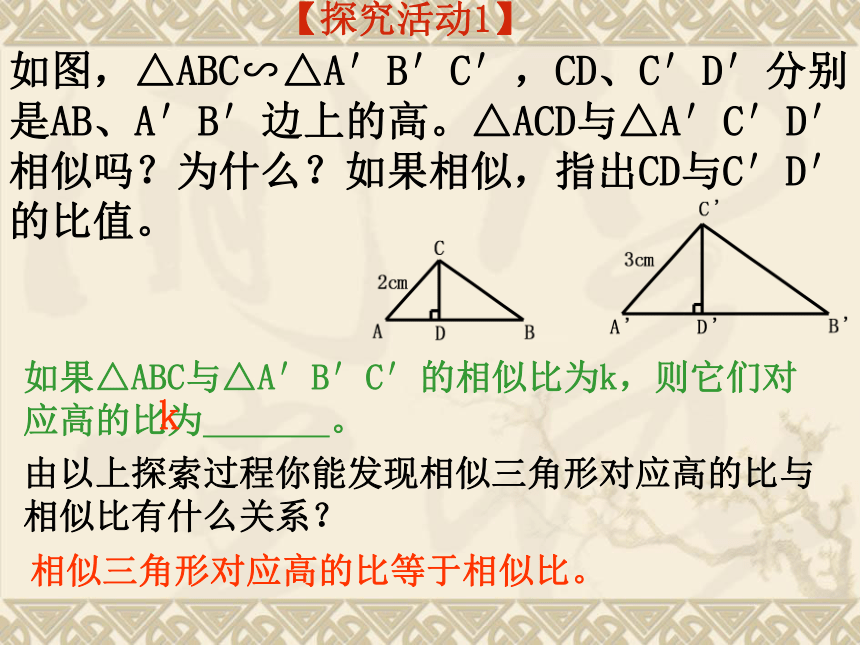
如图,△ABC∽△A′B′C′,CD、C′D′分别
是AB、A′B′边上的高。△ACD与△A′C′D′相似吗?为什么?如果相似,指出CD与C′D′的比值。
【探究活动1】
由以上探索过程你能发现相似三角形对应高的比与相似比有什么关系?
如果△ABC与△A′B′C′的相似比为k,则它们对应高的比为 。
相似三角形对应高的比等于相似比。
k
如图:已知△ABC∽△A′B′C′,相似比为k。CE、C′E′分别是∠ACB和∠A′C′B′的平分线,则CE与C′E′的比是多少?请证明你的结论。
【探究活动2】
k
由以上探索过程你又发现了相似三角形的什么性质?
如图:已知△ABC∽△A′B′C′,相似比为k。CF、C′F′分别是AB和A′B′边上的中线,则CF与C′F′的比是多少?请证明你的结论。
【探究活动3】
定理:相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比。
变式拓展探究:
如果把角平分线、中线变为对应角的三等分线、四等分线、…n等分线,对应边的三等分线、四等分线、…n等分线,那么它们也具有特殊关系吗?
类比探究相似三角形对应中线的比、
对应角平分线的比
【探究活动4】
【探究活动4】(变式拓展)
如图3-32,已知△ABC ∽△A'B'C',△ABC 与△A'B'C'的相似比为k.
(1)若 ,则 等于多少
(2)若 ,则 等于多少
(3)你还能提出哪些问题?与同伴交流.
相似三角形对应角的n等分线的比,对应边的n等分线的比都等于相似比。
【探究活动4】(变式拓展)
∵△ABC∽△A′B′C′
CF、C′F′分别是AB、A′B′
边的中线
∴
(3)
∵△ABC∽△A′B′C′
CD、C′D′分别是AB、A′B′
边上的高
∴
(1)
∵△ABC∽△A′B′C′
CE、C′E′分别是∠ACB、
∠A′C′B′ 的平分线
∴
(2)
【数学格式】
【学以致用】
8︰3
1、△ABC∽△A′B′C′,AD和A′D′是它们
的对应角平分线。已知AD=8cm, A′D′=3cm,
则△ABC与△A′B′C′对应高的比为 。
2、△ABC∽△A′B′C′,BD和B′D′是它们
的对应中线, , B′D′=4cm,则BD的长为 。
3、两个相似三角形中一组对应角平分线的长分
别是2cm和5cm,则这两个三角形的相似比为 。
在这两个三角形的一组对应中线中,如果较短的
中线是3cm,那么较长的中线的长为 。
6cm
2︰5
【学以致用】
4、如图,小章自制了一个小孔成像装置,其中纸筒的长度为15cm。他准备了一支长为20cm的蜡烛,想要得到高度为5cm的像,蜡烛应放在距离纸筒 cm的地方。
60
如图,AD是△ABC的高,点P、Q在BC边上,点R 在AC边上,点S在AB边上,BC=60cm,AD=40cm. 四边形PQRS是正方形。 (1)△ASR与△ABC相似吗?为什么? (2)求正方形PQRS的边长。
【拓展应用】
【课后作业】
1、如图,矩形EFGH内接于△ABC,且边FG落在BC上,AD⊥BC,垂足为D,交EH于点M.若BC=3,AD=2,EF= EH,求EH的长。
2、已知△ABC∽△A'B'C',BD和B'D‘是它们 的对应中线, = ,B'D'=4cm,求BD的长.
3、两个相似三角形中一组对应角平分线的长分别是2cm和5cm,求这两个三角形的相似比。在这两个三角形的一组对应中线中,如果较短的中线是3cm,那么较长的中线多长?
到目前为止,我们学习了相似三角形的哪些性质?请你总结出来。
【课堂小结】
相似三角形的性质:
1、相似三角形的对应角相等,对应边成比例。
2、相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比。
4.7相似三角形的性质(一)
北师大版九上第四章《图形的相似》
还记得相似三角形的定义吗 还记得相似多边形的对应边、对应角有什么关系吗?
在两个相似三角形中是否只有对应角相等、对应边成比例这个性质呢?本节课我们将研究相似三角形的其他性质.
【回顾与反思】
相似三角形的对应边成比例、对应角相等。
学习目标:
经历探索相似三角形中对应线段比值与相似比的关系的过程,理解相似三角形的性质。
利用相似三角形的性质解决一些实际问题.
1、相似三角形有哪些判别方法?
2、相似三角形有什么性质?
相似三角形的的判别方法:
(1)两角分别相等的两个三角形相似
(2)两边成比例且夹角相等的两个三角形相似
(3)三边成比例的两个三角形相似
相似三角形的性质:
相似三角形的对应角相等,对应边成比例。
【复习引入】
3、如图,△ABC∽△A′B′C′。
(1)△ABC与△A′B′C′的相似比为 。
(2)请说出△ABC与△A′B′C′各角的关系,
各边的关系。
【复习引入】
2︰3
角:∠A=∠A′ ∠B=∠B′ ∠C=∠C′
边:
如图,△ABC∽△A′B′C′,CD、C′D′分别
是AB、A′B′边上的高。△ACD与△A′C′D′相似吗?为什么?如果相似,指出CD与C′D′的比值。
【探究活动1】
由以上探索过程你能发现相似三角形对应高的比与相似比有什么关系?
如果△ABC与△A′B′C′的相似比为k,则它们对应高的比为 。
相似三角形对应高的比等于相似比。
k
如图:已知△ABC∽△A′B′C′,相似比为k。CE、C′E′分别是∠ACB和∠A′C′B′的平分线,则CE与C′E′的比是多少?请证明你的结论。
【探究活动2】
k
由以上探索过程你又发现了相似三角形的什么性质?
如图:已知△ABC∽△A′B′C′,相似比为k。CF、C′F′分别是AB和A′B′边上的中线,则CF与C′F′的比是多少?请证明你的结论。
【探究活动3】
定理:相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比。
变式拓展探究:
如果把角平分线、中线变为对应角的三等分线、四等分线、…n等分线,对应边的三等分线、四等分线、…n等分线,那么它们也具有特殊关系吗?
类比探究相似三角形对应中线的比、
对应角平分线的比
【探究活动4】
【探究活动4】(变式拓展)
如图3-32,已知△ABC ∽△A'B'C',△ABC 与△A'B'C'的相似比为k.
(1)若 ,则 等于多少
(2)若 ,则 等于多少
(3)你还能提出哪些问题?与同伴交流.
相似三角形对应角的n等分线的比,对应边的n等分线的比都等于相似比。
【探究活动4】(变式拓展)
∵△ABC∽△A′B′C′
CF、C′F′分别是AB、A′B′
边的中线
∴
(3)
∵△ABC∽△A′B′C′
CD、C′D′分别是AB、A′B′
边上的高
∴
(1)
∵△ABC∽△A′B′C′
CE、C′E′分别是∠ACB、
∠A′C′B′ 的平分线
∴
(2)
【数学格式】
【学以致用】
8︰3
1、△ABC∽△A′B′C′,AD和A′D′是它们
的对应角平分线。已知AD=8cm, A′D′=3cm,
则△ABC与△A′B′C′对应高的比为 。
2、△ABC∽△A′B′C′,BD和B′D′是它们
的对应中线, , B′D′=4cm,则BD的长为 。
3、两个相似三角形中一组对应角平分线的长分
别是2cm和5cm,则这两个三角形的相似比为 。
在这两个三角形的一组对应中线中,如果较短的
中线是3cm,那么较长的中线的长为 。
6cm
2︰5
【学以致用】
4、如图,小章自制了一个小孔成像装置,其中纸筒的长度为15cm。他准备了一支长为20cm的蜡烛,想要得到高度为5cm的像,蜡烛应放在距离纸筒 cm的地方。
60
如图,AD是△ABC的高,点P、Q在BC边上,点R 在AC边上,点S在AB边上,BC=60cm,AD=40cm. 四边形PQRS是正方形。 (1)△ASR与△ABC相似吗?为什么? (2)求正方形PQRS的边长。
【拓展应用】
【课后作业】
1、如图,矩形EFGH内接于△ABC,且边FG落在BC上,AD⊥BC,垂足为D,交EH于点M.若BC=3,AD=2,EF= EH,求EH的长。
2、已知△ABC∽△A'B'C',BD和B'D‘是它们 的对应中线, = ,B'D'=4cm,求BD的长.
3、两个相似三角形中一组对应角平分线的长分别是2cm和5cm,求这两个三角形的相似比。在这两个三角形的一组对应中线中,如果较短的中线是3cm,那么较长的中线多长?
到目前为止,我们学习了相似三角形的哪些性质?请你总结出来。
【课堂小结】
相似三角形的性质:
1、相似三角形的对应角相等,对应边成比例。
2、相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
