2021-2022学年华东师大版数学九年级下册27.1.2 圆的对称性 - 垂径定理 课件(30张)
文档属性
| 名称 | 2021-2022学年华东师大版数学九年级下册27.1.2 圆的对称性 - 垂径定理 课件(30张) |

|
|
| 格式 | zip | ||
| 文件大小 | 929.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 14:24:51 | ||
图片预览






文档简介
(共30张PPT)
——垂径定理及其推论
垂径定理及其推论
【教学目标】
1.知识目标:①通过观察实验,使学生理解圆的轴对称性;
②掌握垂径定理,理解其证明,并会用它解决有关的证明与计算问题;
③掌握辅助线的作法——过圆心作一条与弦垂直的线段。
2.能力目标:①通过定理探究,培养学生观察、分析、逻辑思维和归纳概括能力;
②向学生渗透“由特殊到一般,再由一般到特殊”的基本思想方法。
3.情感目标:①结合本课教学特点,向学生进行爱国主义教育和美育渗透;
②激发学生探究、发现数学问题的兴趣和欲望。
教学重点:
垂径定理及其应用
教学难点:
垂径定理的证明
知识回顾
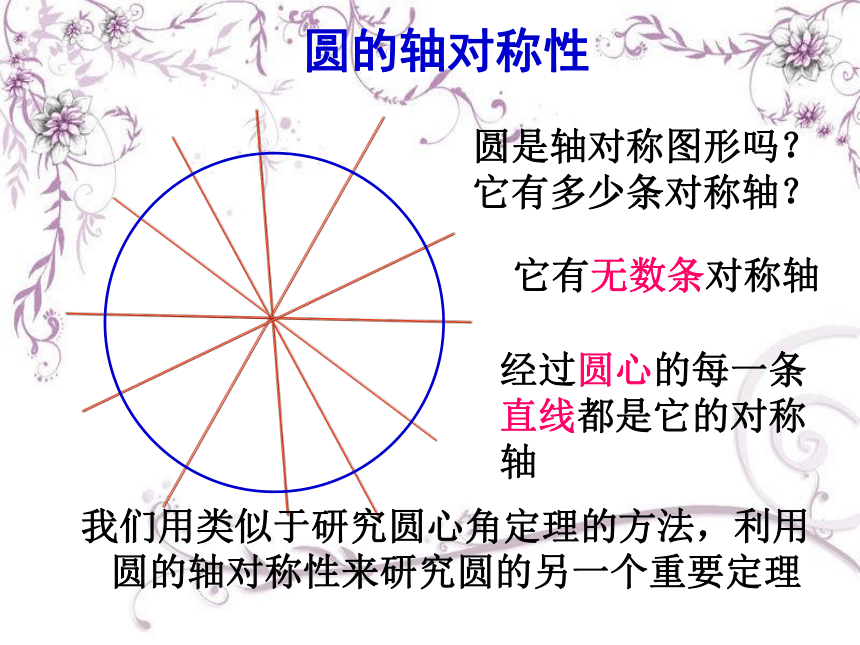
圆是轴对称图形吗?它有多少条对称轴?
它有无数条对称轴
经过圆心的每一条直线都是它的对称轴
圆的轴对称性
我们用类似于研究圆心角定理的方法,利用圆的轴对称性来研究圆的另一个重要定理
·
O
A
B
D
C
E
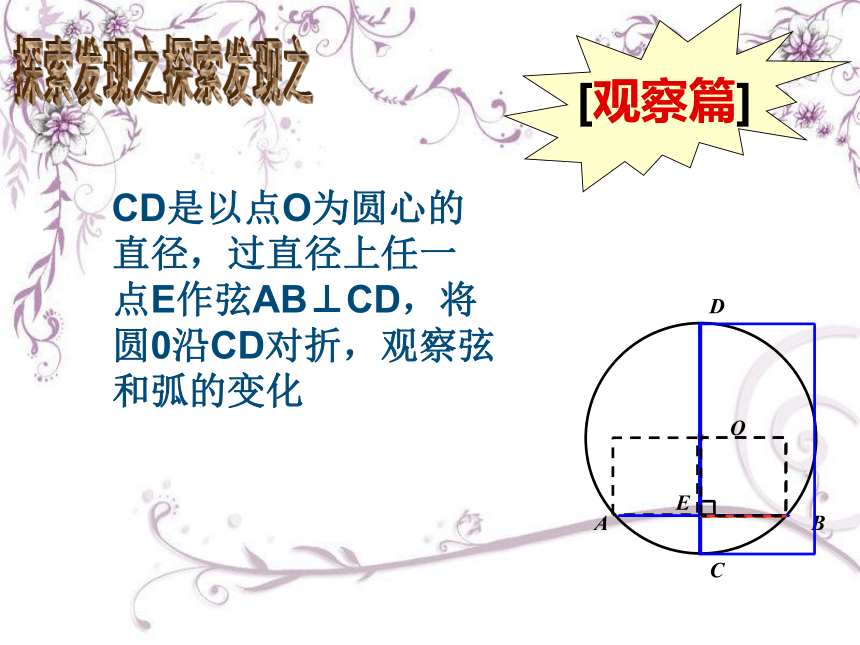
CD是以点O为圆心的直径,过直径上任一点E作弦AB⊥CD,将圆0沿CD对折,观察弦和弧的变化
[观察篇]
[发现篇]
猜想 :垂直于弦的直径平分弦,并且平分弦所对的两条弧。
即:如果CD过圆心,且垂直于AB,则AE=BE,弧AD=弧BD,弧AC=弧BC
垂直于弦的直径
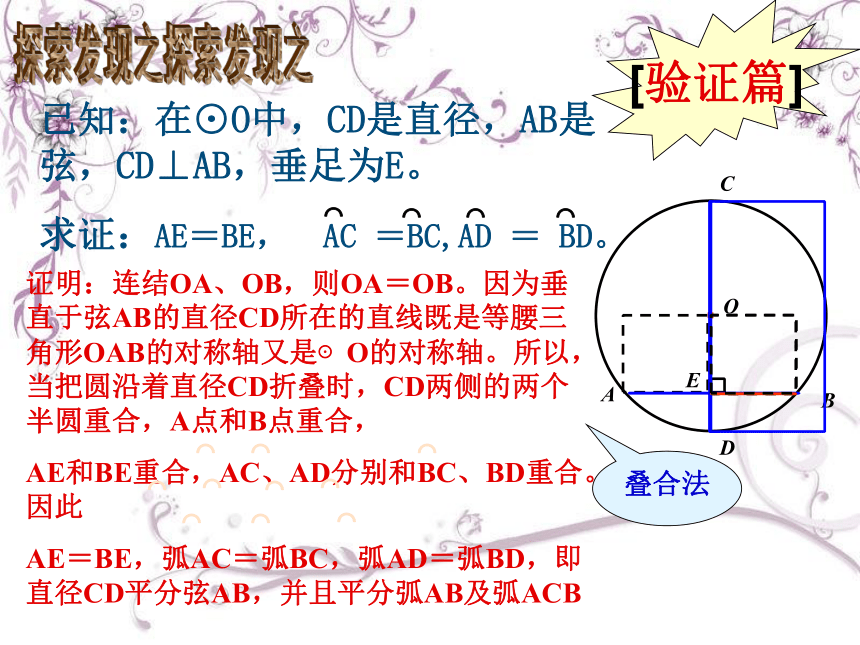
[验证篇]
⌒
证明:连结OA、OB,则OA=OB。因为垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴又是⊙O的对称轴。所以,当把圆沿着直径CD折叠时,CD两侧的两个半圆重合,A点和B点重合,
AE和BE重合,AC、AD分别和BC、BD重合。因此
AE=BE,弧AC=弧BC,弧AD=弧BD,即直径CD平分弦AB,并且平分弧AB及弧ACB
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。
求证:AE=BE, AC =BC,AD = BD。
⌒
⌒
⌒
⌒
叠合法
·
O
A
B
C
D
E
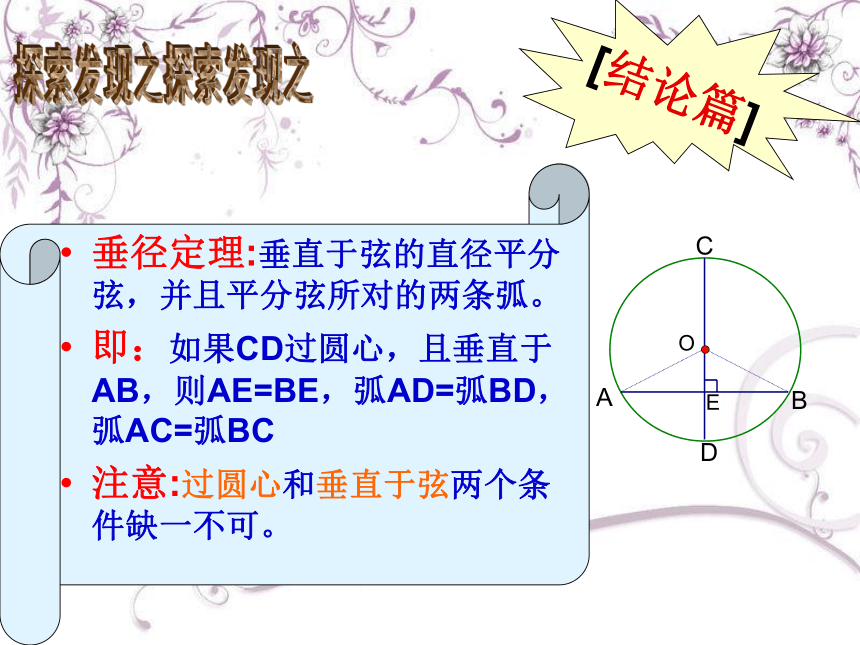
[结论篇]
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
即:如果CD过圆心,且垂直于AB,则AE=BE,弧AD=弧BD,弧AC=弧BC
注意:过圆心和垂直于弦两个条件缺一不可。
O
E
D
C
B
A
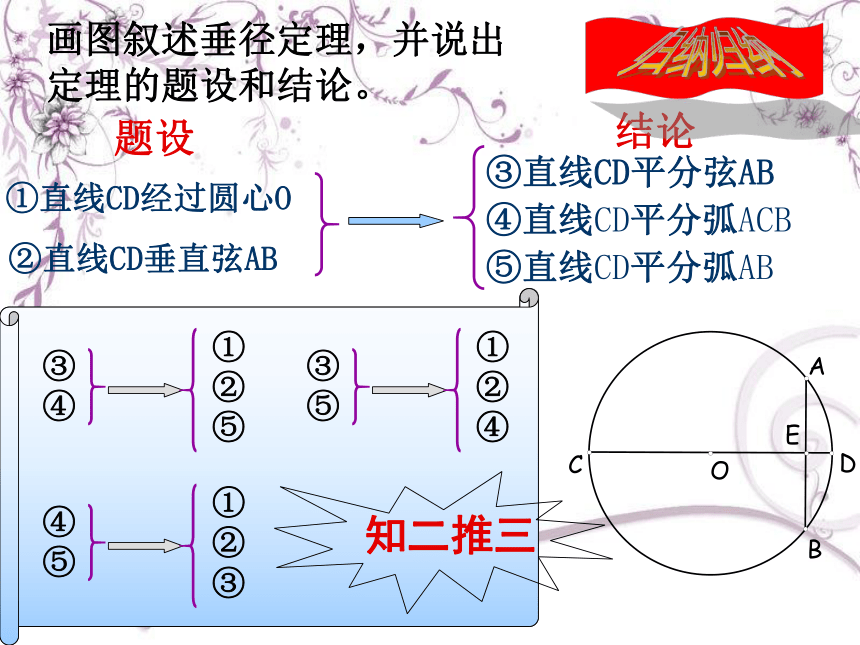
画图叙述垂径定理,并说出定理的题设和结论。
题设
结论
①直线CD经过圆心O
②直线CD垂直弦AB
③直线CD平分弦AB
④直线CD平分弧ACB
⑤直线CD平分弧AB
想一想:如果将题设和结论中的5个条件适当互换,情况会怎样?
① ③
②④⑤
② ③
① ④⑤
① ④
②③ ⑤
②④
① ③ ⑤
①②⑤
①②④
④⑤
①②③
③④
③
⑤
知二推三
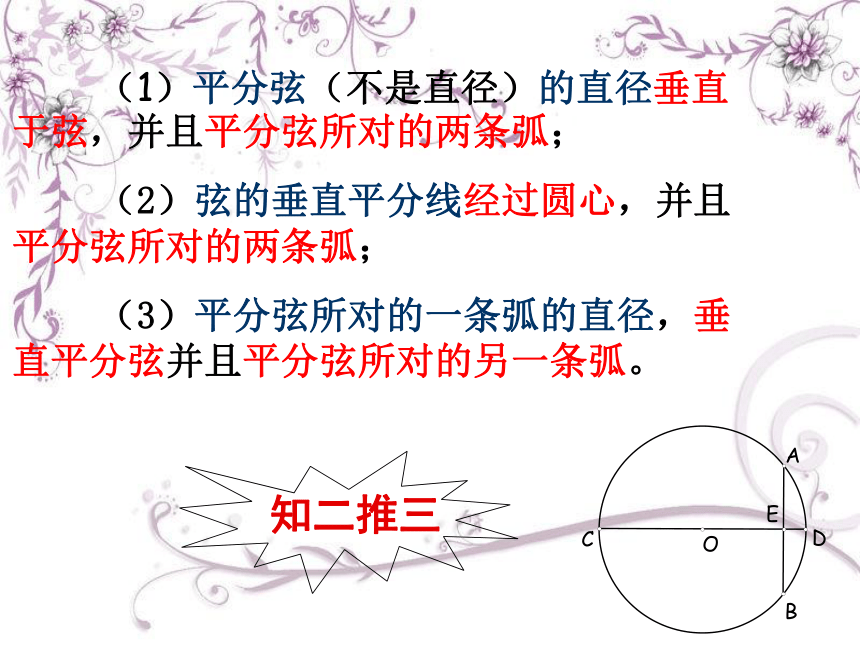
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦并且平分弦所对的另一条弧。
知二推三
注:①“平分弦的直径垂直于弦”这个推论中弦一定是非直径的弦(因为任何两条直径都互相平分);
②垂径定理反映出圆是轴对称图形这一特性,这是证明线段、角相等以及垂直关系的重要依据;
③垂径定理的结论有三个:直径平分弦,直径平分弦所对的优弧,直径平分弦所对的劣弧.连同两个题设共计五个结论,如果以其中任意两个作为已知,那么其余三个都是成立的;
④解决圆有关弦的问题,经常过圆心作弦的垂线,以便应用垂径定理解题,一般利用圆心到弦的距离(弦心距)、过弦的端点的半径、弦长的一半构成直角三角形,将计算线段的问题转化为解直角三角形的问题。
注意:定理中的两个条件(直径(过圆心),垂直于弦)缺一不可!
例题讲解
例1.如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E,并且CD=4,EM=6,求⊙O的半径.
【分析】因为M是⊙O弦CD的中点,根据垂径定理,EM⊥CD,则CM=DM=2,在Rt△COM中,有OC2=CM2+OM2,进而可求得半径OC.
.
【解答】解:连接OC
∵M是⊙O弦CD的中点,
根据垂径定理:EM⊥CD,
设圆的半径是x米,
在Rt△COM中,有OC2=CM2+OM2,
即:x2=22+(6﹣x)2,
例题讲解
例2.⊙O中,直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,且∠DEB=60°,求CD的长.
【分析】作OP⊥CD于P,连接OD,根据正弦的定义求出OP,根据勾股定理求出PD,根据垂径定理计算.
【解答】解:作OP⊥CD于P,连接OD,
∴CP=PD,
∵AE=1,EB=5,
∴AB=6,∴OE=2,
例题讲解
变式练习
在Rt△OPE中,OP=OE sin∠DEB= ,
∴PD= = ,
∴CD=2PD=2 (cm).
【点评】本题考查的是垂径定理,掌握垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
1.下列命题中正确的是( )
A.弦的垂线平分弦所对的弧 B.平分弦的直径垂直于这条弦
C.过弦中点的直线必过圆心 D.弦所对的两条弧的中点连线垂直平分弦
D
变式练习
C
2.如图,△ABC中,AB=5,AC=4,BC=2,以A为圆心AB为半径作圆A,延长BC交圆A于点D,则CD长为( )
A.5 B.4 C. D.2
3.如图,在⊙O中,直径AB=10,弦DE⊥AB于点C,若OC:OB=3:5,连接DO,则DE的长为( )
A.3 B.4 C.6 D.8
D
变式练习
20
12或4
5.如图是水平放置的水管截面示意图,已知水管的半径为50cm,水面宽AB=80cm,则水深CD约为 cm.
4.AB是⊙O的弦,OM⊥AB,垂足为M,连接OA.若△AOM中有一个角是30°,OM=2 ,则弦AB的长为 .
例题讲解
例3.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)求证:E是OB的中点;
(2)若AB=16,求CD的长.
【分析】(1)要证明:E是OB的中点,只要求证
即证明∠OCE=30°即可.
(2)在直角△OCE中,根据勾股定理就可以解得CE
的长,进而求出CD的长.
【解答】(1)证明:连接AC,如图
∵直径AB垂直于弦CD于点E,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.即:△ACD是等边三角形,
∴∠FCD=30°,
∴点E为OB的中点;
在Rt△COE中,
例题讲解
(2)解:在Rt△OCE中,AB=16,
又∵BE=OE,
∴OE=4,
【点评】本题考查垂径定理,勾股定理等知识,解题的
关键是灵活运用所学知识解决问题,属于中考常考题型.
1、对垂径定理的理解 (1)证明定理的方法——“叠合法”
(2)定理是解决有关弦的问题的重要方法 (3)定理中反映的弦的中点,弦所对的两条弧的中点都集中在“垂直于弦的直径”上。圆、弦又关于直径所在的直线对称。
2、关于垂径定理的运用 (1)辅助线的常用作法 (2)注意把问题化为解直角三角形的问题
教学反思:
垂径定理是圆的重要性质之一,也是全章的基础之一,在整章中占有举足轻重的地位,是今后研究圆与其他图形位置关系和数量关系的基础,这些知识在日常生活和生产中有广泛的应用。由于垂径定理及其推论反映了圆的重要性质,是证明线段相等、角相等、垂直关系的重要依据,因此,它是整节书的重点及难点
课后作业
C
B
C
1.如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则
①∠COE=∠DOE,②CE=DE,
其中正确的结论是( )
A.①②④ B.②③④ C.①②③④ D.①②
2.如图,在⊙O中,弦AB的长为16cm,圆心O到AB的距离为6cm,则⊙O的半径是( )
A.6cm B.10cm C.8cm D.20cm
3.如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )
A.AE=OE B.∠AOC=60° C.CE=DE D.OE= CE
课后作业
B
A
7.5
5.如图,坐标平面上,A、B两点分别为圆P与x轴y轴的交点,有一直线L通过P点且与AB垂直,C点为L与y轴的交点.若A、B、C的坐标分别为(a,0),(0,4),(0,﹣5),其中a<0,则a的值为何?( )
4.点P是⊙O内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为( )
A.3cm B.4cm C.5cm D.6cm、
6.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=12cm,则球的半径为 cm.
课后作业
1或7
7.已知⊙O的直径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=8cm,CD=6cm,则AB与CD之间的距离为 cm.
8.如图,AB为⊙O的直径,CD为弦,过A、B分别作
AE⊥CD、BF⊥CD,分别交直线CD于E、F.
(1)求证:CE=DF;
(2)若AB=20cm,CD=10cm,求AE+BF的值.
【分析】(1)过点O作OG⊥CD于G,AE∥OG∥BF,
根据平行线分线段成比例定理与垂径定理即可证明;
(2)OG是直角梯形ABFE的中位线,则AE+BF=2OG,
连接OC,根据勾股定理和垂径定理即可求得OG的长,进而求解.
【解答】(1)证明:过点O作OG⊥CD于G,
∵AE⊥EF,OG⊥EF,BF⊥EF,
∴AE∥OG∥BF,
又∵OA=OB,
课后作业
∴GE=GF,
∵OG过圆心O,OG⊥CD,
∴CG=GD,
∴EG﹣CG=GF﹣GD,
即CE=DF;
∵OG过圆心O,OG⊥CD,
【点评】本题主要考查了垂径定理的应用,利用垂径
定理可以把求弦长或圆心角的问题转化为解直角三角形的问题.
课后作业
9.一座桥,桥拱是圆弧形(水面以上部分),测量时只测
到桥下水面宽AB为16m(如图),桥拱最高处离水面4m.
(1)求桥拱半径;
(2)若大雨过后,桥下面河面宽度为12m,问水面涨高了多少?
【分析】已知到桥下水面宽AB为16m,即是已知圆的弦长,已知桥拱最高处离水面4m,就是已知弦心距,可以利用垂径定理转化为解直角三角形的问题
【解答】解:(1)如图所示,设点O为AB的圆心,
设⊙O半径为xm,则在Rt△AOD中,
OA2=AD2+OD2,即x2=82+(x-4)2,
解得x=10,所以桥拱的半径为10m;
课后作业
【点评】上涨高度即是弦心距的差.是正确解本题的关键.
(2)设河水上涨到EF位置(如图所示),
这时EF=12m,EF∥AB,有OC⊥EF(垂足为M),
连接OE,则有OE=10m,
OD=OC﹣CD=10﹣4=6(m),
DM=OM﹣OD=8﹣6=2(m).
课后作业
10.如图,∠C=90°,以AC为半径的圆C与AB相交于
点D.若AC=3,CB=4,求BD长.
【分析】根据勾股定理求得AB的长,再点C作
CE⊥AB于点E,由垂径定理得出AE,即可得出BD长.
【解答】解:(1)∵在三角形ABC中,
∠ACB=90°,AC=3,BC=4,
过点C作CE⊥AB于点E,则AD=2AE,
∵∠CAE=∠CAB,∠AEC=∠ACB=90°,
∴△ACE∽△ABC,
∴AC2=AE AB,即32=AE×5
∴AE=1.8,
∴AD=2AE=2×1.8=3.6
∴BD=AB﹣AD=5﹣3.6=1.4.
【点评】本题考查了垂径定理以及勾股定理,熟练掌
握垂径定理、勾股定理的具体内容是解题的关键.
——垂径定理及其推论
垂径定理及其推论
【教学目标】
1.知识目标:①通过观察实验,使学生理解圆的轴对称性;
②掌握垂径定理,理解其证明,并会用它解决有关的证明与计算问题;
③掌握辅助线的作法——过圆心作一条与弦垂直的线段。
2.能力目标:①通过定理探究,培养学生观察、分析、逻辑思维和归纳概括能力;
②向学生渗透“由特殊到一般,再由一般到特殊”的基本思想方法。
3.情感目标:①结合本课教学特点,向学生进行爱国主义教育和美育渗透;
②激发学生探究、发现数学问题的兴趣和欲望。
教学重点:
垂径定理及其应用
教学难点:
垂径定理的证明
知识回顾
圆是轴对称图形吗?它有多少条对称轴?
它有无数条对称轴
经过圆心的每一条直线都是它的对称轴
圆的轴对称性
我们用类似于研究圆心角定理的方法,利用圆的轴对称性来研究圆的另一个重要定理
·
O
A
B
D
C
E
CD是以点O为圆心的直径,过直径上任一点E作弦AB⊥CD,将圆0沿CD对折,观察弦和弧的变化
[观察篇]
[发现篇]
猜想 :垂直于弦的直径平分弦,并且平分弦所对的两条弧。
即:如果CD过圆心,且垂直于AB,则AE=BE,弧AD=弧BD,弧AC=弧BC
垂直于弦的直径
[验证篇]
⌒
证明:连结OA、OB,则OA=OB。因为垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴又是⊙O的对称轴。所以,当把圆沿着直径CD折叠时,CD两侧的两个半圆重合,A点和B点重合,
AE和BE重合,AC、AD分别和BC、BD重合。因此
AE=BE,弧AC=弧BC,弧AD=弧BD,即直径CD平分弦AB,并且平分弧AB及弧ACB
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。
求证:AE=BE, AC =BC,AD = BD。
⌒
⌒
⌒
⌒
叠合法
·
O
A
B
C
D
E
[结论篇]
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
即:如果CD过圆心,且垂直于AB,则AE=BE,弧AD=弧BD,弧AC=弧BC
注意:过圆心和垂直于弦两个条件缺一不可。
O
E
D
C
B
A
画图叙述垂径定理,并说出定理的题设和结论。
题设
结论
①直线CD经过圆心O
②直线CD垂直弦AB
③直线CD平分弦AB
④直线CD平分弧ACB
⑤直线CD平分弧AB
想一想:如果将题设和结论中的5个条件适当互换,情况会怎样?
① ③
②④⑤
② ③
① ④⑤
① ④
②③ ⑤
②④
① ③ ⑤
①②⑤
①②④
④⑤
①②③
③④
③
⑤
知二推三
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦并且平分弦所对的另一条弧。
知二推三
注:①“平分弦的直径垂直于弦”这个推论中弦一定是非直径的弦(因为任何两条直径都互相平分);
②垂径定理反映出圆是轴对称图形这一特性,这是证明线段、角相等以及垂直关系的重要依据;
③垂径定理的结论有三个:直径平分弦,直径平分弦所对的优弧,直径平分弦所对的劣弧.连同两个题设共计五个结论,如果以其中任意两个作为已知,那么其余三个都是成立的;
④解决圆有关弦的问题,经常过圆心作弦的垂线,以便应用垂径定理解题,一般利用圆心到弦的距离(弦心距)、过弦的端点的半径、弦长的一半构成直角三角形,将计算线段的问题转化为解直角三角形的问题。
注意:定理中的两个条件(直径(过圆心),垂直于弦)缺一不可!
例题讲解
例1.如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E,并且CD=4,EM=6,求⊙O的半径.
【分析】因为M是⊙O弦CD的中点,根据垂径定理,EM⊥CD,则CM=DM=2,在Rt△COM中,有OC2=CM2+OM2,进而可求得半径OC.
.
【解答】解:连接OC
∵M是⊙O弦CD的中点,
根据垂径定理:EM⊥CD,
设圆的半径是x米,
在Rt△COM中,有OC2=CM2+OM2,
即:x2=22+(6﹣x)2,
例题讲解
例2.⊙O中,直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,且∠DEB=60°,求CD的长.
【分析】作OP⊥CD于P,连接OD,根据正弦的定义求出OP,根据勾股定理求出PD,根据垂径定理计算.
【解答】解:作OP⊥CD于P,连接OD,
∴CP=PD,
∵AE=1,EB=5,
∴AB=6,∴OE=2,
例题讲解
变式练习
在Rt△OPE中,OP=OE sin∠DEB= ,
∴PD= = ,
∴CD=2PD=2 (cm).
【点评】本题考查的是垂径定理,掌握垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
1.下列命题中正确的是( )
A.弦的垂线平分弦所对的弧 B.平分弦的直径垂直于这条弦
C.过弦中点的直线必过圆心 D.弦所对的两条弧的中点连线垂直平分弦
D
变式练习
C
2.如图,△ABC中,AB=5,AC=4,BC=2,以A为圆心AB为半径作圆A,延长BC交圆A于点D,则CD长为( )
A.5 B.4 C. D.2
3.如图,在⊙O中,直径AB=10,弦DE⊥AB于点C,若OC:OB=3:5,连接DO,则DE的长为( )
A.3 B.4 C.6 D.8
D
变式练习
20
12或4
5.如图是水平放置的水管截面示意图,已知水管的半径为50cm,水面宽AB=80cm,则水深CD约为 cm.
4.AB是⊙O的弦,OM⊥AB,垂足为M,连接OA.若△AOM中有一个角是30°,OM=2 ,则弦AB的长为 .
例题讲解
例3.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)求证:E是OB的中点;
(2)若AB=16,求CD的长.
【分析】(1)要证明:E是OB的中点,只要求证
即证明∠OCE=30°即可.
(2)在直角△OCE中,根据勾股定理就可以解得CE
的长,进而求出CD的长.
【解答】(1)证明:连接AC,如图
∵直径AB垂直于弦CD于点E,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.即:△ACD是等边三角形,
∴∠FCD=30°,
∴点E为OB的中点;
在Rt△COE中,
例题讲解
(2)解:在Rt△OCE中,AB=16,
又∵BE=OE,
∴OE=4,
【点评】本题考查垂径定理,勾股定理等知识,解题的
关键是灵活运用所学知识解决问题,属于中考常考题型.
1、对垂径定理的理解 (1)证明定理的方法——“叠合法”
(2)定理是解决有关弦的问题的重要方法 (3)定理中反映的弦的中点,弦所对的两条弧的中点都集中在“垂直于弦的直径”上。圆、弦又关于直径所在的直线对称。
2、关于垂径定理的运用 (1)辅助线的常用作法 (2)注意把问题化为解直角三角形的问题
教学反思:
垂径定理是圆的重要性质之一,也是全章的基础之一,在整章中占有举足轻重的地位,是今后研究圆与其他图形位置关系和数量关系的基础,这些知识在日常生活和生产中有广泛的应用。由于垂径定理及其推论反映了圆的重要性质,是证明线段相等、角相等、垂直关系的重要依据,因此,它是整节书的重点及难点
课后作业
C
B
C
1.如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则
①∠COE=∠DOE,②CE=DE,
其中正确的结论是( )
A.①②④ B.②③④ C.①②③④ D.①②
2.如图,在⊙O中,弦AB的长为16cm,圆心O到AB的距离为6cm,则⊙O的半径是( )
A.6cm B.10cm C.8cm D.20cm
3.如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )
A.AE=OE B.∠AOC=60° C.CE=DE D.OE= CE
课后作业
B
A
7.5
5.如图,坐标平面上,A、B两点分别为圆P与x轴y轴的交点,有一直线L通过P点且与AB垂直,C点为L与y轴的交点.若A、B、C的坐标分别为(a,0),(0,4),(0,﹣5),其中a<0,则a的值为何?( )
4.点P是⊙O内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为( )
A.3cm B.4cm C.5cm D.6cm、
6.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=12cm,则球的半径为 cm.
课后作业
1或7
7.已知⊙O的直径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=8cm,CD=6cm,则AB与CD之间的距离为 cm.
8.如图,AB为⊙O的直径,CD为弦,过A、B分别作
AE⊥CD、BF⊥CD,分别交直线CD于E、F.
(1)求证:CE=DF;
(2)若AB=20cm,CD=10cm,求AE+BF的值.
【分析】(1)过点O作OG⊥CD于G,AE∥OG∥BF,
根据平行线分线段成比例定理与垂径定理即可证明;
(2)OG是直角梯形ABFE的中位线,则AE+BF=2OG,
连接OC,根据勾股定理和垂径定理即可求得OG的长,进而求解.
【解答】(1)证明:过点O作OG⊥CD于G,
∵AE⊥EF,OG⊥EF,BF⊥EF,
∴AE∥OG∥BF,
又∵OA=OB,
课后作业
∴GE=GF,
∵OG过圆心O,OG⊥CD,
∴CG=GD,
∴EG﹣CG=GF﹣GD,
即CE=DF;
∵OG过圆心O,OG⊥CD,
【点评】本题主要考查了垂径定理的应用,利用垂径
定理可以把求弦长或圆心角的问题转化为解直角三角形的问题.
课后作业
9.一座桥,桥拱是圆弧形(水面以上部分),测量时只测
到桥下水面宽AB为16m(如图),桥拱最高处离水面4m.
(1)求桥拱半径;
(2)若大雨过后,桥下面河面宽度为12m,问水面涨高了多少?
【分析】已知到桥下水面宽AB为16m,即是已知圆的弦长,已知桥拱最高处离水面4m,就是已知弦心距,可以利用垂径定理转化为解直角三角形的问题
【解答】解:(1)如图所示,设点O为AB的圆心,
设⊙O半径为xm,则在Rt△AOD中,
OA2=AD2+OD2,即x2=82+(x-4)2,
解得x=10,所以桥拱的半径为10m;
课后作业
【点评】上涨高度即是弦心距的差.是正确解本题的关键.
(2)设河水上涨到EF位置(如图所示),
这时EF=12m,EF∥AB,有OC⊥EF(垂足为M),
连接OE,则有OE=10m,
OD=OC﹣CD=10﹣4=6(m),
DM=OM﹣OD=8﹣6=2(m).
课后作业
10.如图,∠C=90°,以AC为半径的圆C与AB相交于
点D.若AC=3,CB=4,求BD长.
【分析】根据勾股定理求得AB的长,再点C作
CE⊥AB于点E,由垂径定理得出AE,即可得出BD长.
【解答】解:(1)∵在三角形ABC中,
∠ACB=90°,AC=3,BC=4,
过点C作CE⊥AB于点E,则AD=2AE,
∵∠CAE=∠CAB,∠AEC=∠ACB=90°,
∴△ACE∽△ABC,
∴AC2=AE AB,即32=AE×5
∴AE=1.8,
∴AD=2AE=2×1.8=3.6
∴BD=AB﹣AD=5﹣3.6=1.4.
【点评】本题考查了垂径定理以及勾股定理,熟练掌
握垂径定理、勾股定理的具体内容是解题的关键.
