2021-2022学年北师大版七年级数学上册5.3.1 列一元一次方程解决实际问题的基本方法 同步测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学上册5.3.1 列一元一次方程解决实际问题的基本方法 同步测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 64.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 14:39:23 | ||
图片预览


文档简介
5.3.1 列一元一次方程解决实际问题的基本方法同步测试卷 2021-2022学年北师大版七年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共7小题,共21分)
学校七年级师生共466人准备参加社会实践活动.现已预备了49座和37座两种客车共10辆,刚好坐满.设49座客车x辆,则根据题意可列方程为 ( )
A. B.
C. D.
某月的月历上竖列相邻的三个数的和是39,则该列的第一个数是()
A. B. C. D.
小丽在2月的月历上圈出5个数,呈“十字框”形,它们的和是55,则中间的数是()
A. B. C. D.
编写如下数学谜题:3×2□+5=□2,“□”内要求填写同一个数字,若设“□”内的数字为x.则列出方程正确的是 ( )
A. B.
C. D.
程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁?意思是有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人?下列求解结果正确的是()
A. 大和尚人,小和尚人 B. 大和尚人,小和尚人
C. 大和尚人,小和尚人 D. 大、小和尚各人
甲、乙、丙三村合修一条公路,计划出工84人,按3:4:7出工,求各村出工的人数.
设甲、乙、丙三村分别派3x人、4x人、7x人,依题意,得3x+4x+7x=84;
设甲村派x人,依题意,得x+4x+7x=84;设乙村派x人,依题意,得x+x+x=84;
设丙村派x人,依题意,得3x+4x+x=84.上面所列方程中正确的有( )
A. 个 B. 个 C. 个 D. 个
A,B,C,D四支足球队分在同一小组进行单循环足球比赛,争夺出线权.比赛规则规定:胜一场得3分,平一场得1分,负一场得0分,小组中积分最高的两个队(有且只有两个队)出线.小组赛结束后,如果A队没有全胜,那么A队的积分至少要( )分才能保证一定出线.【注:单循环比赛就是小组内的每一个队都要和其他队赛一场】
A. B. C. D.
二、填空题(本大题共6小题,共18分)
(1)已知一个三角形三边的长度之比为2:3:4,若设其中最短边的长度为2x,则该三角形的周长可表示为 .
(2)篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队14场比赛得到23分.若设该队胜的场数为x,则可列方程为 .
(3)有一列数,按一定的规律排列成,-1,3,-9,27,-81,….若其中某三个相邻数的和是-567,则这三个数中第一个数是 .
被誉为“最美高铁”的长春至珲春城际铁路途经许多隧道和桥梁,其中隧道累计长度与桥梁累计长度之和为342 km,隧道累计长度的2倍比桥梁累计长度长36 km.则隧道累计长度为 km,桥梁累计长度为 km.
(1)公元前1700年的古埃及纸草书中,记载着一个数学问题:“它的全部,加上它的七分之一,其和等于19.”此问题中“它”的值为 .
(2)小麦磨成面粉,质量减轻16%.如果要得到336 kg面粉,那么需要 kg小麦.
(3)小强同学生日的月数减去日数为2,月数的两倍与日数相加为31,则小强同学生日的月数与日数的和为 .
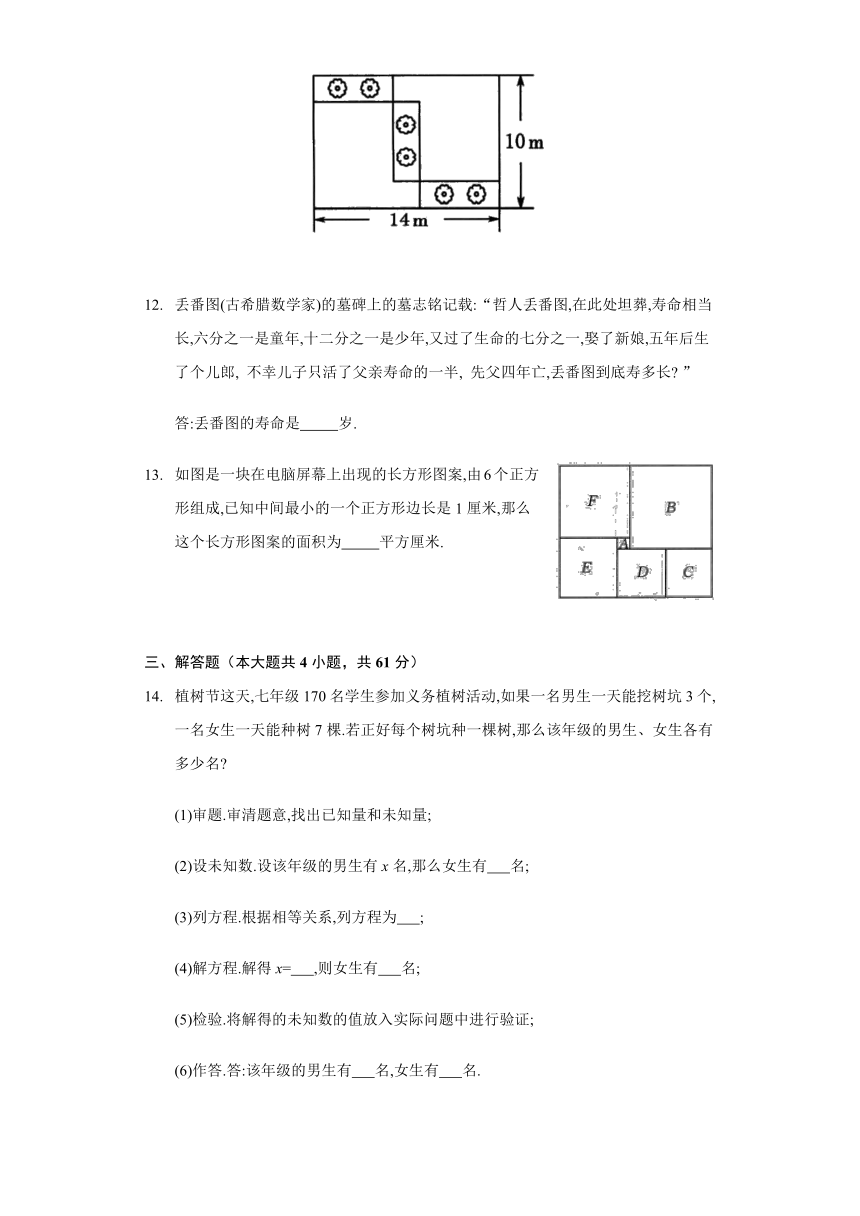
水仙花是漳州市市花,如图,在长为14 m、宽为10 m的长方形展厅中,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的长为 m.
丢番图(古希腊数学家)的墓碑上的墓志铭记载:“哲人丢番图,在此处坦葬,寿命相当长,六分之一是童年,十二分之一是少年,又过了生命的七分之一,娶了新娘,五年后生了个儿郎, 不幸儿子只活了父亲寿命的一半, 先父四年亡,丢番图到底寿多长 ”
答:丢番图的寿命是 岁.
如图是一块在电脑屏幕上出现的长方形图案,由6个正方形组成,已知中间最小的一个正方形边长是1厘米,那么这个长方形图案的面积为 平方厘米.
三、解答题(本大题共4小题,共61分)
植树节这天,七年级170名学生参加义务植树活动,如果一名男生一天能挖树坑3个,一名女生一天能种树7棵.若正好每个树坑种一棵树,那么该年级的男生、女生各有多少名
(1)审题.审清题意,找出已知量和未知量;
(2)设未知数.设该年级的男生有x名,那么女生有 名;
(3)列方程.根据相等关系,列方程为 ;
(4)解方程.解得x= ,则女生有 名;
(5)检验.将解得的未知数的值放入实际问题中进行验证;
(6)作答.答:该年级的男生有 名,女生有 名.
中秋节时阿柚制作的广式月饼、蛋黄酥、凤梨酥的数量比为2:1:3,其中只有制作广式月饼和蛋黄酥时使用咸蛋黄.若阿柚制作每个广式月饼使用2颗咸蛋黄,制作每个蛋黄酥使用1颗咸蛋黄,且总共使用120颗咸蛋黄,问他制作了多少个凤梨酥?
中国古代人民很早就在生产生活中发现了许多有趣的数学问题,《孙子算经》中有这样一个问题,原文:今有三人共车,二车空;二人共车,九人步.问人与车各几何 这道题的意思是:今有若干人乘车,若每3人共乘一车,最终剩余2辆车;若每2人共乘一车,最终剩余9人无车可乘.问共有多少人,多少辆车
在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.
(1)七年级(2)班有男生、女生各多少人
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底
参考答案
1.【答案】A
2.【答案】A
3.【答案】C
4.【答案】D
5.【答案】A
6.【答案】A
7.【答案】A
8.【答案】9x
2x+1×(14-x)=23
-81
9.【答案】126
216
10.【答案】
400
20
11.【答案】6
12.【答案】84
13.【答案】143
14.【答案】(2)(170-x)
(3)3x=7(170-x)
(4)119;51
(6)119;51
15.【答案】解:设阿柚制作了x个蛋黄酥,
则制作了2x个广式月饼,3x个凤梨酥.
根据题意,
得2×2x+x=120,
解得x=24,
此时3x=72.
答:他制作了72个凤梨酥.
16.【答案】解:设共有x人,
根据题意得+2=,
解得x=39,
所以=15(辆).
答:共有39人,15辆车.
17.【答案】解:(1)设七年级(2)班有女生x人,则有男生(x-2)人,由题意得x+(x-2)=44,
解得x=23,所以x-2=21,
则七年级(2)班有女生23人,男生21人.
(2)设分配a名学生剪筒身,则剪筒底的学生有(44-a)名,由题意得50a2=120(44-a),
解得a=24,所以44-a=20,
则分配24名学生剪筒身,20名学生剪筒底.
第6页,共6页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共7小题,共21分)
学校七年级师生共466人准备参加社会实践活动.现已预备了49座和37座两种客车共10辆,刚好坐满.设49座客车x辆,则根据题意可列方程为 ( )
A. B.
C. D.
某月的月历上竖列相邻的三个数的和是39,则该列的第一个数是()
A. B. C. D.
小丽在2月的月历上圈出5个数,呈“十字框”形,它们的和是55,则中间的数是()
A. B. C. D.
编写如下数学谜题:3×2□+5=□2,“□”内要求填写同一个数字,若设“□”内的数字为x.则列出方程正确的是 ( )
A. B.
C. D.
程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁?意思是有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人?下列求解结果正确的是()
A. 大和尚人,小和尚人 B. 大和尚人,小和尚人
C. 大和尚人,小和尚人 D. 大、小和尚各人
甲、乙、丙三村合修一条公路,计划出工84人,按3:4:7出工,求各村出工的人数.
设甲、乙、丙三村分别派3x人、4x人、7x人,依题意,得3x+4x+7x=84;
设甲村派x人,依题意,得x+4x+7x=84;设乙村派x人,依题意,得x+x+x=84;
设丙村派x人,依题意,得3x+4x+x=84.上面所列方程中正确的有( )
A. 个 B. 个 C. 个 D. 个
A,B,C,D四支足球队分在同一小组进行单循环足球比赛,争夺出线权.比赛规则规定:胜一场得3分,平一场得1分,负一场得0分,小组中积分最高的两个队(有且只有两个队)出线.小组赛结束后,如果A队没有全胜,那么A队的积分至少要( )分才能保证一定出线.【注:单循环比赛就是小组内的每一个队都要和其他队赛一场】
A. B. C. D.
二、填空题(本大题共6小题,共18分)
(1)已知一个三角形三边的长度之比为2:3:4,若设其中最短边的长度为2x,则该三角形的周长可表示为 .
(2)篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队14场比赛得到23分.若设该队胜的场数为x,则可列方程为 .
(3)有一列数,按一定的规律排列成,-1,3,-9,27,-81,….若其中某三个相邻数的和是-567,则这三个数中第一个数是 .
被誉为“最美高铁”的长春至珲春城际铁路途经许多隧道和桥梁,其中隧道累计长度与桥梁累计长度之和为342 km,隧道累计长度的2倍比桥梁累计长度长36 km.则隧道累计长度为 km,桥梁累计长度为 km.
(1)公元前1700年的古埃及纸草书中,记载着一个数学问题:“它的全部,加上它的七分之一,其和等于19.”此问题中“它”的值为 .
(2)小麦磨成面粉,质量减轻16%.如果要得到336 kg面粉,那么需要 kg小麦.
(3)小强同学生日的月数减去日数为2,月数的两倍与日数相加为31,则小强同学生日的月数与日数的和为 .
水仙花是漳州市市花,如图,在长为14 m、宽为10 m的长方形展厅中,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的长为 m.
丢番图(古希腊数学家)的墓碑上的墓志铭记载:“哲人丢番图,在此处坦葬,寿命相当长,六分之一是童年,十二分之一是少年,又过了生命的七分之一,娶了新娘,五年后生了个儿郎, 不幸儿子只活了父亲寿命的一半, 先父四年亡,丢番图到底寿多长 ”
答:丢番图的寿命是 岁.
如图是一块在电脑屏幕上出现的长方形图案,由6个正方形组成,已知中间最小的一个正方形边长是1厘米,那么这个长方形图案的面积为 平方厘米.
三、解答题(本大题共4小题,共61分)
植树节这天,七年级170名学生参加义务植树活动,如果一名男生一天能挖树坑3个,一名女生一天能种树7棵.若正好每个树坑种一棵树,那么该年级的男生、女生各有多少名
(1)审题.审清题意,找出已知量和未知量;
(2)设未知数.设该年级的男生有x名,那么女生有 名;
(3)列方程.根据相等关系,列方程为 ;
(4)解方程.解得x= ,则女生有 名;
(5)检验.将解得的未知数的值放入实际问题中进行验证;
(6)作答.答:该年级的男生有 名,女生有 名.
中秋节时阿柚制作的广式月饼、蛋黄酥、凤梨酥的数量比为2:1:3,其中只有制作广式月饼和蛋黄酥时使用咸蛋黄.若阿柚制作每个广式月饼使用2颗咸蛋黄,制作每个蛋黄酥使用1颗咸蛋黄,且总共使用120颗咸蛋黄,问他制作了多少个凤梨酥?
中国古代人民很早就在生产生活中发现了许多有趣的数学问题,《孙子算经》中有这样一个问题,原文:今有三人共车,二车空;二人共车,九人步.问人与车各几何 这道题的意思是:今有若干人乘车,若每3人共乘一车,最终剩余2辆车;若每2人共乘一车,最终剩余9人无车可乘.问共有多少人,多少辆车
在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.
(1)七年级(2)班有男生、女生各多少人
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底
参考答案
1.【答案】A
2.【答案】A
3.【答案】C
4.【答案】D
5.【答案】A
6.【答案】A
7.【答案】A
8.【答案】9x
2x+1×(14-x)=23
-81
9.【答案】126
216
10.【答案】
400
20
11.【答案】6
12.【答案】84
13.【答案】143
14.【答案】(2)(170-x)
(3)3x=7(170-x)
(4)119;51
(6)119;51
15.【答案】解:设阿柚制作了x个蛋黄酥,
则制作了2x个广式月饼,3x个凤梨酥.
根据题意,
得2×2x+x=120,
解得x=24,
此时3x=72.
答:他制作了72个凤梨酥.
16.【答案】解:设共有x人,
根据题意得+2=,
解得x=39,
所以=15(辆).
答:共有39人,15辆车.
17.【答案】解:(1)设七年级(2)班有女生x人,则有男生(x-2)人,由题意得x+(x-2)=44,
解得x=23,所以x-2=21,
则七年级(2)班有女生23人,男生21人.
(2)设分配a名学生剪筒身,则剪筒底的学生有(44-a)名,由题意得50a2=120(44-a),
解得a=24,所以44-a=20,
则分配24名学生剪筒身,20名学生剪筒底.
第6页,共6页
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
