2021-2022学年人教版八年级数学上册11.1.1 三角形的边同步测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册11.1.1 三角形的边同步测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 78.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 14:46:02 | ||
图片预览


文档简介
11.1.1 三角形的边同步测试卷 2021-2022学年人教版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共9小题,共36分)
三角形按边分类可以用如图所示的集合来表示,则图中小椭圆圈里的A表示( )
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 等边三角形
在下列长度的三条线段中,不能组成三角形的是( )
A. ,, B. ,,
C. ,, D. ,,
一个三角形的三边长之比是2:2:1,周长是10,此三角形按边分是( )
A. 等腰三角形 B. 等边三角形 C. 不等边三角形 D. 以上都不对
已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为( )
A. B. C. D.
若a,b,c为ABC的三边长,且满足|c-3|+=0,则a的值不可能是( )
A. B. C. D.
若实数m,n满足等式|m- 2|+=0,且m,n恰好是等腰三角形ABC的两条边的长,则ABC的周长是( )
A. B. C. 或 D.
下列说法正确的是( )
等腰三角形是等边三角形;
三角形按边分类可分为等腰三角形、等边三角形和不等边三角形;
等腰三角形至少有两条边相等.
A. B. C. D.
长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )
A. B. C. D.
已知n是正整数,若一个三角形的三边长分别是n+2,n+8,3n,则满足条件的n的值有( )
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共5小题,共20分)
若三角形的两边长分别是5和2,且第三边的长度是偶数,则第三边的长度可能是__ ___.
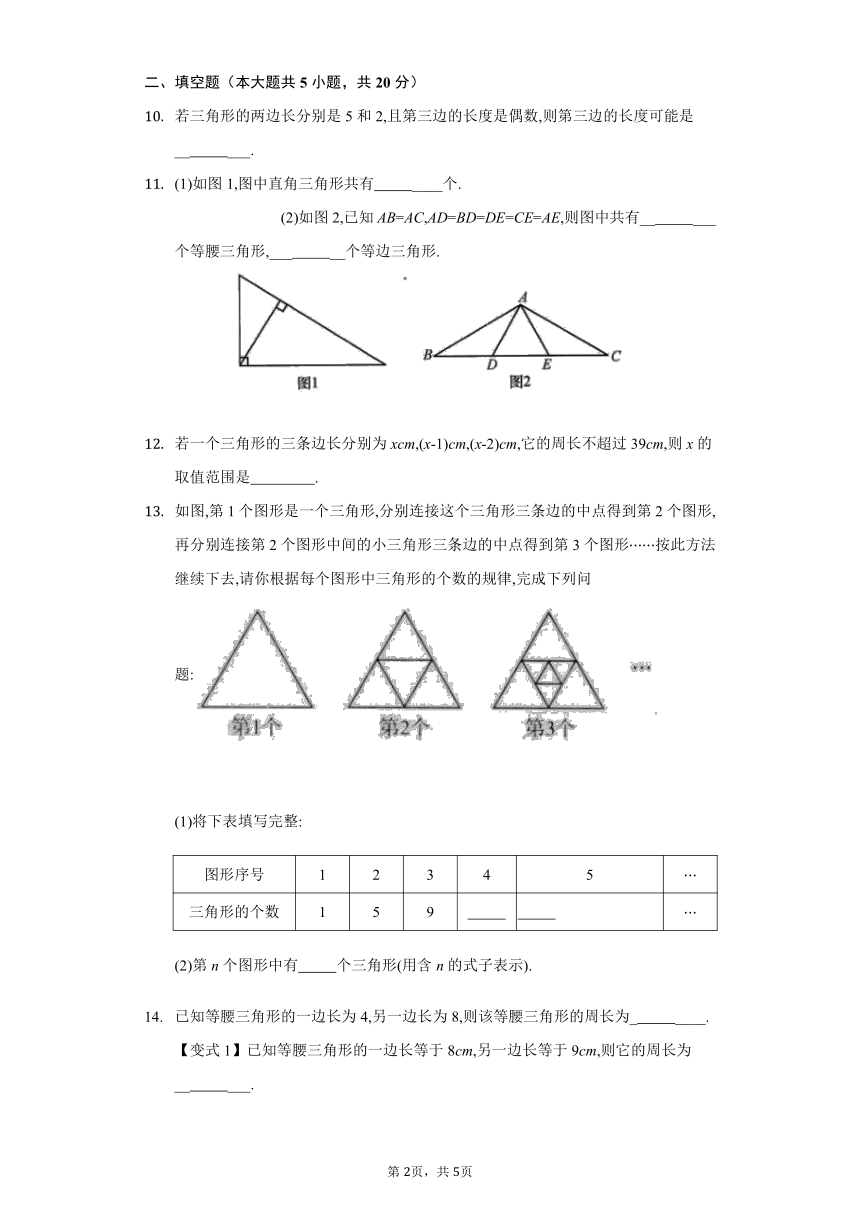
(1)如图1,图中直角三角形共有 ____个.
(2)如图2,已知AB=AC,AD=BD=DE=CE=AE,则图中共有__ ___个等腰三角形,___ __个等边三角形.
若一个三角形的三条边长分别为xcm,(x-1)cm,(x-2)cm,它的周长不超过39cm,则x的取值范围是 .
如图,第1个图形是一个三角形,分别连接这个三角形三条边的中点得到第2个图形,再分别连接第2个图形中间的小三角形三条边的中点得到第3个图形按此方法继续下去,请你根据每个图形中三角形的个数的规律,完成下列问题:
(1)将下表填写完整:
图形序号 1 2 3 4 5
三角形的个数 1 5 9
(2)第n个图形中有 个三角形(用含n的式子表示).
已知等腰三角形的一边长为4,另一边长为8,则该等腰三角形的周长为_ ____.
【变式1】已知等腰三角形的一边长等于8cm,另一边长等于9cm,则它的周长为__ ___.
【变式2】等腰三角形的一边长等于6cm,周长等于28cm,则其他两边的长为__ ___.
三、解答题(本大题共2小题,共44分)
已知a,b,c是ABC的三边长.
(1)若a,b,c满足|a-b|+=0,试判断ABC的形状;
(2)若a,b,c满足(a-b)(b-c)=0,试判断ABC的形状;
(3)化简:|a-b-c|+|b-c-a|+|c-a-b|.
16.如图,点P是ABC内部的一点.
(1)测量线段AB,AC,PB,PC的长度,根据测量结果比较AB+AC与PB+PC的大小.
(2)改变点P的位置,上述结论还成立吗
(3)你能说明上述结论为什么成立吗
参考答案
1.【答案】D
2.【答案】C
3.【答案】A
4.【答案】C
5.【答案】D
6.【答案】B
7.【答案】D
8.【答案】B
9.【答案】D
10.【答案】4或6
11.【答案】3 4 1
12.【答案】
13.【答案】13
17
(4n-3)
14.【答案】20
25cm或26cm
11cm,11cm
15.【答案】解:(1)|a-b|+=0,
a-b=0且b-c=0,
a=b=c,
ABC为等边三角形;
(2)(a-b)(b-c)=0,
a-b=0或b-c=0,
a=b或b=c,
ABC为等腰三角形;
(3)a,b,c是ABC的三边长,
a-b-c<0,b-c-a<0,c-a- b<0,
原式=-a+b+c-b+c+a-c+ a+b=a+b+c.
16.【答案】解:(1)AB+AC>PB+PC.
(2)改变点P的位置,上述结论还成立.
(3)连接AP,延长BP交AC于点E,
在ABE中,有AB+AE>BE=BP+PE.
在CEP中,有PE+CE>PC.
+,得AB+AE+PE+CE>BP+PE+PC,
即AB+AC+PE>BP+PE+PC,
AB+AC>BP+PC.
第4页,共5页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共9小题,共36分)
三角形按边分类可以用如图所示的集合来表示,则图中小椭圆圈里的A表示( )
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 等边三角形
在下列长度的三条线段中,不能组成三角形的是( )
A. ,, B. ,,
C. ,, D. ,,
一个三角形的三边长之比是2:2:1,周长是10,此三角形按边分是( )
A. 等腰三角形 B. 等边三角形 C. 不等边三角形 D. 以上都不对
已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为( )
A. B. C. D.
若a,b,c为ABC的三边长,且满足|c-3|+=0,则a的值不可能是( )
A. B. C. D.
若实数m,n满足等式|m- 2|+=0,且m,n恰好是等腰三角形ABC的两条边的长,则ABC的周长是( )
A. B. C. 或 D.
下列说法正确的是( )
等腰三角形是等边三角形;
三角形按边分类可分为等腰三角形、等边三角形和不等边三角形;
等腰三角形至少有两条边相等.
A. B. C. D.
长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )
A. B. C. D.
已知n是正整数,若一个三角形的三边长分别是n+2,n+8,3n,则满足条件的n的值有( )
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共5小题,共20分)
若三角形的两边长分别是5和2,且第三边的长度是偶数,则第三边的长度可能是__ ___.
(1)如图1,图中直角三角形共有 ____个.
(2)如图2,已知AB=AC,AD=BD=DE=CE=AE,则图中共有__ ___个等腰三角形,___ __个等边三角形.
若一个三角形的三条边长分别为xcm,(x-1)cm,(x-2)cm,它的周长不超过39cm,则x的取值范围是 .
如图,第1个图形是一个三角形,分别连接这个三角形三条边的中点得到第2个图形,再分别连接第2个图形中间的小三角形三条边的中点得到第3个图形按此方法继续下去,请你根据每个图形中三角形的个数的规律,完成下列问题:
(1)将下表填写完整:
图形序号 1 2 3 4 5
三角形的个数 1 5 9
(2)第n个图形中有 个三角形(用含n的式子表示).
已知等腰三角形的一边长为4,另一边长为8,则该等腰三角形的周长为_ ____.
【变式1】已知等腰三角形的一边长等于8cm,另一边长等于9cm,则它的周长为__ ___.
【变式2】等腰三角形的一边长等于6cm,周长等于28cm,则其他两边的长为__ ___.
三、解答题(本大题共2小题,共44分)
已知a,b,c是ABC的三边长.
(1)若a,b,c满足|a-b|+=0,试判断ABC的形状;
(2)若a,b,c满足(a-b)(b-c)=0,试判断ABC的形状;
(3)化简:|a-b-c|+|b-c-a|+|c-a-b|.
16.如图,点P是ABC内部的一点.
(1)测量线段AB,AC,PB,PC的长度,根据测量结果比较AB+AC与PB+PC的大小.
(2)改变点P的位置,上述结论还成立吗
(3)你能说明上述结论为什么成立吗
参考答案
1.【答案】D
2.【答案】C
3.【答案】A
4.【答案】C
5.【答案】D
6.【答案】B
7.【答案】D
8.【答案】B
9.【答案】D
10.【答案】4或6
11.【答案】3 4 1
12.【答案】
13.【答案】13
17
(4n-3)
14.【答案】20
25cm或26cm
11cm,11cm
15.【答案】解:(1)|a-b|+=0,
a-b=0且b-c=0,
a=b=c,
ABC为等边三角形;
(2)(a-b)(b-c)=0,
a-b=0或b-c=0,
a=b或b=c,
ABC为等腰三角形;
(3)a,b,c是ABC的三边长,
a-b-c<0,b-c-a<0,c-a- b<0,
原式=-a+b+c-b+c+a-c+ a+b=a+b+c.
16.【答案】解:(1)AB+AC>PB+PC.
(2)改变点P的位置,上述结论还成立.
(3)连接AP,延长BP交AC于点E,
在ABE中,有AB+AE>BE=BP+PE.
在CEP中,有PE+CE>PC.
+,得AB+AE+PE+CE>BP+PE+PC,
即AB+AC+PE>BP+PE+PC,
AB+AC>BP+PC.
第4页,共5页
