2021-2022学年人教版八年级数学上册11.3.2 多边形的内角和 同步测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册11.3.2 多边形的内角和 同步测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 161.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 14:50:18 | ||
图片预览

文档简介
11.3.2 多边形的内角和同步测试卷 2021-2022学年人教版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共9小题,共36分)
若正多边形的内角和是,则该正多边形的一个外角为( )
A. B. C. D.
若一个正n边形的每个内角为,则这个正n边形的所有对角线的条数是( )
A. B. C. D.
若一个多边形的每个外角都等于,则从此多边形的一个顶点出发可作的对角线共有( )
A. 条 B. 条 C. 条 D. 条
一个凸多边形的内角和比它的外角和的3倍还多,则这个多边形是( )
A. 九边形 B. 八边形 C. 七边形 D. 六边形
游戏中有数学智慧,找起点游戏规定:从起点走五段相等直路之后回到起点,要求每走完一段直路后向右边偏行,成功的招数不止一招,可助我们成功的一招是( )
A. 每走完一段直路后沿向右偏方向行走
B. 每段直路要短
C. 每走完一段直路后沿向右偏方向行走
D. 每段直路要长
一个多边形切去一个角后,形成的另一个多边形的内角和为,那么原多边形的边数为( )
A. B. 或 C. 或 D. 或或
一副三角尺如图所示摆放,则与的数量关系为( )
A. B.
C. D.
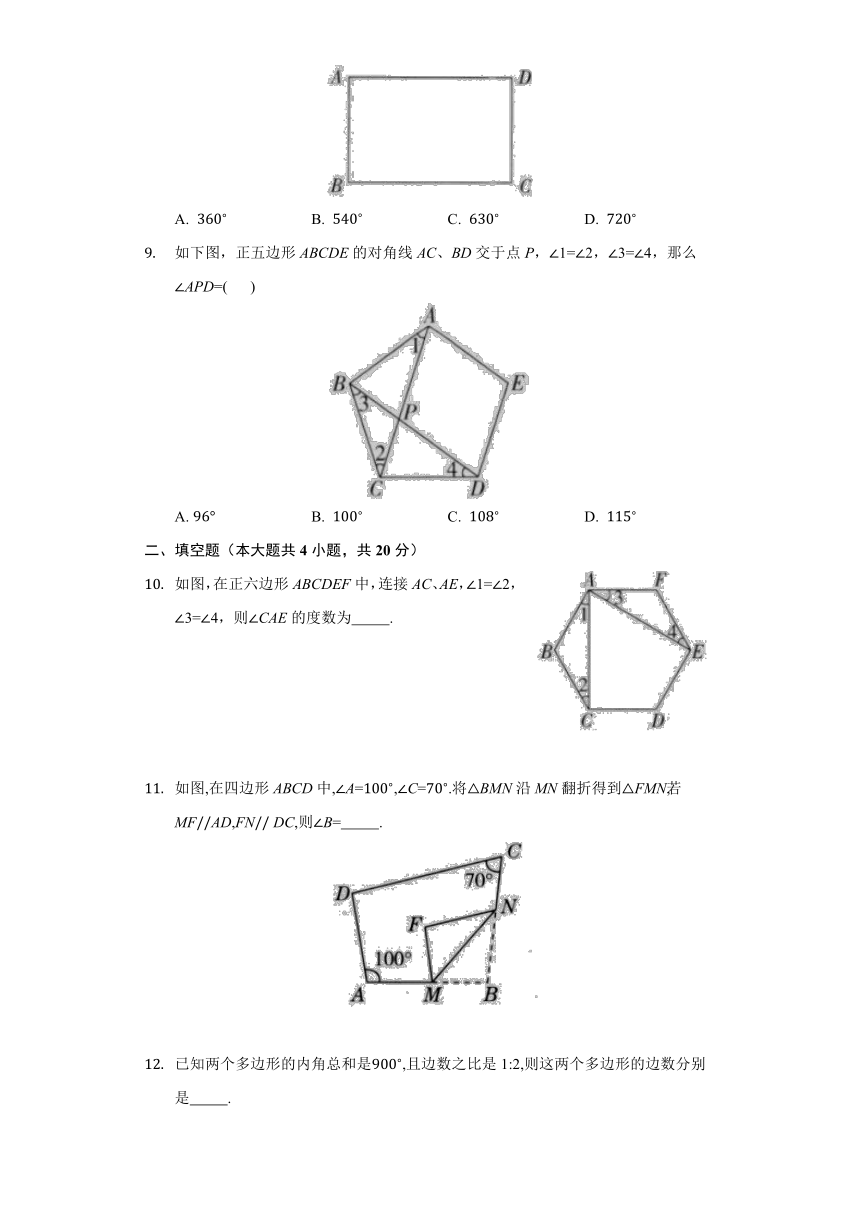
下图为长方形ABCD,一条直线将该长方形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )
A. B. C. D.
如下图,正五边形ABCDE的对角线AC、BD交于点P,1=2,3=4,那么APD=( )
A. B. C. D.
二、填空题(本大题共4小题,共20分)
如图,在正六边形ABCDEF中,连接AC、AE,1=2,3=4,则CAE的度数为 .
如图,在四边形ABCD中,A=,C=.将BMN沿MN翻折得到FMN,若MFAD,FN DC,则B= .
已知两个多边形的内角总和是,且边数之比是1:2,则这两个多边形的边数分别是 .
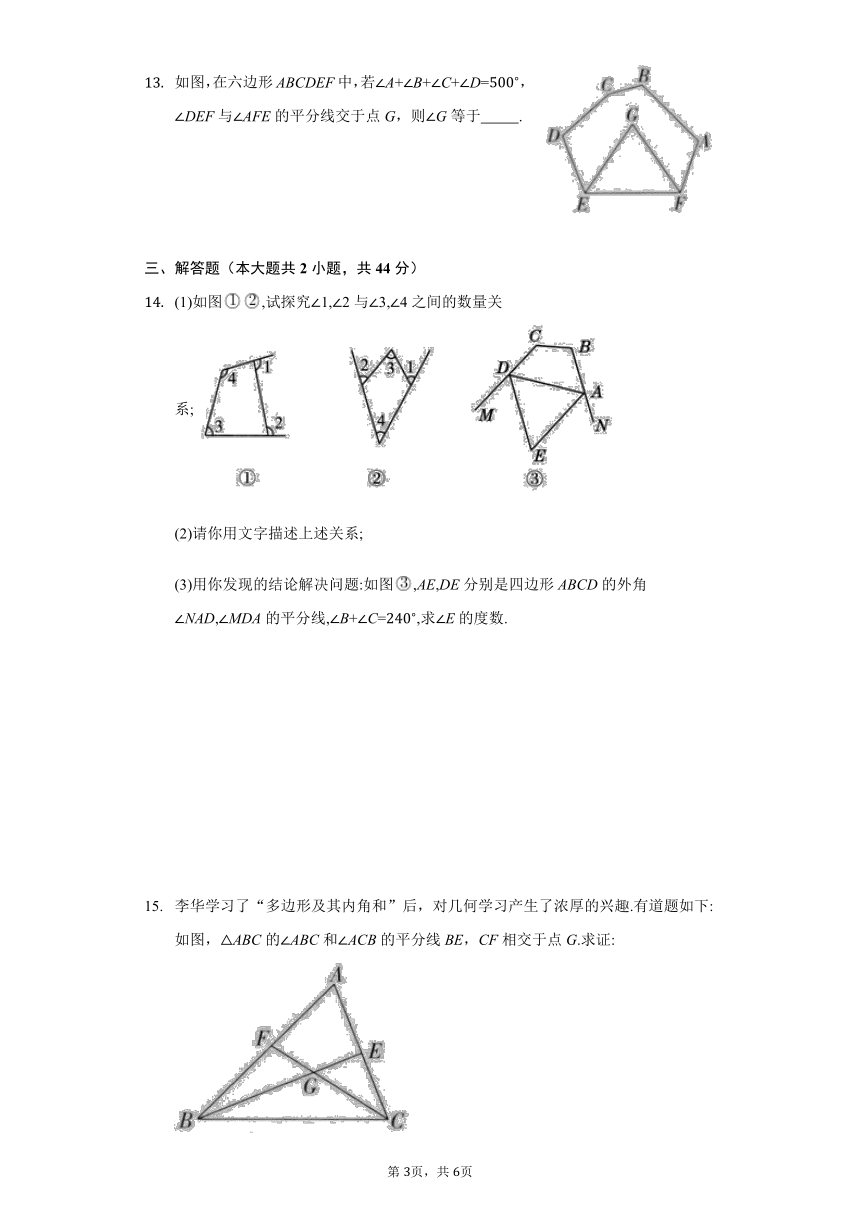
如图,在六边形ABCDEF中,若A+B+C+D=,DEF与AFE的平分线交于点G,则G等于 .
三、解答题(本大题共2小题,共44分)
(1)如图,试探究1,2与3,4之间的数量关系;
(2)请你用文字描述上述关系;
(3)用你发现的结论解决问题:如图,AE,DE分别是四边形ABCD的外角NAD,MDA的平分线,B+C=,求E的度数.
李华学习了“多边形及其内角和”后,对几何学习产生了浓厚的兴趣.有道题如下:
如图,ABC的ABC和ACB的平分线BE,CF相交于点G.求证:
(1)BGC=-(ABC+ACB);
(2)BGC=+A.
李华发现这个题目其实是解决“三角形的一个内角与另外两个内角的平分线所夹的钝角之间有何种关系”这个问题,他把这个问题改编如下:
问题1:若将ABC改为任意四边形ABCD呢?如图,在四边形ABCD中,DP、CP分别平分ADC和BCD,请你利用上述结论探究P与A+B的数量关系,并说明理由;
问题2:若将上题中的四边形ABCD改为六边形ABC-DEF呢?如图所示,请你利用上述结论探究P与A+B+E+F的数量关系,并说明理由.
参考答案
1.【答案】C
2.【答案】C
3.【答案】A
4.【答案】A
5.【答案】A
6.【答案】D
7.【答案】B
8.【答案】C
9.【答案】C
10.【答案】
11.【答案】
12.【答案】3,6
13.【答案】
14.【答案】解:(1)设1的邻补角为5,2的邻补角为6.
3,4,5,6是四边形的四个内角,
3+4+5+6=.
3+4=-(5+6).
1+5=,2+6=,
1+2=-(5+6).
1+2=3+4.
(2)在一个四边形中,两个外角的和等于与它们不相邻的两个内角的和.
(3)B+C=,
MDA+NAD=.
AE,DE分别是NAD,MDA的平分线,
ADE=MDA,DAE= NAD.
ADE+DAE=(MDA+ NAD)=.
E=-(ADE+DAE)= .
15.【答案】解:问题1:P=(A+B).
理由:DP、CP分别平分ADC和BCD,
PDC=ADC,PCD=BCD,
P=-PDC-PCD
=-ADC-BCD
=-(ADC+BCD)
=-(-A-B)
=(A+B).
问题2:P=(A+B+E+F)-.
理由:六边形ABCDEF的内角和为(6-2)=,
DP、CP分别平分EDC和BCD,
PDC= EDC,PCD=BCD,
P = -PDC-PCD
=-EDC-BCD
=-(EDC+BCD)
= - (- A- B- E- F)
= (A + B + E + F)- .
第5页,共6页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共9小题,共36分)
若正多边形的内角和是,则该正多边形的一个外角为( )
A. B. C. D.
若一个正n边形的每个内角为,则这个正n边形的所有对角线的条数是( )
A. B. C. D.
若一个多边形的每个外角都等于,则从此多边形的一个顶点出发可作的对角线共有( )
A. 条 B. 条 C. 条 D. 条
一个凸多边形的内角和比它的外角和的3倍还多,则这个多边形是( )
A. 九边形 B. 八边形 C. 七边形 D. 六边形
游戏中有数学智慧,找起点游戏规定:从起点走五段相等直路之后回到起点,要求每走完一段直路后向右边偏行,成功的招数不止一招,可助我们成功的一招是( )
A. 每走完一段直路后沿向右偏方向行走
B. 每段直路要短
C. 每走完一段直路后沿向右偏方向行走
D. 每段直路要长
一个多边形切去一个角后,形成的另一个多边形的内角和为,那么原多边形的边数为( )
A. B. 或 C. 或 D. 或或
一副三角尺如图所示摆放,则与的数量关系为( )
A. B.
C. D.
下图为长方形ABCD,一条直线将该长方形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )
A. B. C. D.
如下图,正五边形ABCDE的对角线AC、BD交于点P,1=2,3=4,那么APD=( )
A. B. C. D.
二、填空题(本大题共4小题,共20分)
如图,在正六边形ABCDEF中,连接AC、AE,1=2,3=4,则CAE的度数为 .
如图,在四边形ABCD中,A=,C=.将BMN沿MN翻折得到FMN,若MFAD,FN DC,则B= .
已知两个多边形的内角总和是,且边数之比是1:2,则这两个多边形的边数分别是 .
如图,在六边形ABCDEF中,若A+B+C+D=,DEF与AFE的平分线交于点G,则G等于 .
三、解答题(本大题共2小题,共44分)
(1)如图,试探究1,2与3,4之间的数量关系;
(2)请你用文字描述上述关系;
(3)用你发现的结论解决问题:如图,AE,DE分别是四边形ABCD的外角NAD,MDA的平分线,B+C=,求E的度数.
李华学习了“多边形及其内角和”后,对几何学习产生了浓厚的兴趣.有道题如下:
如图,ABC的ABC和ACB的平分线BE,CF相交于点G.求证:
(1)BGC=-(ABC+ACB);
(2)BGC=+A.
李华发现这个题目其实是解决“三角形的一个内角与另外两个内角的平分线所夹的钝角之间有何种关系”这个问题,他把这个问题改编如下:
问题1:若将ABC改为任意四边形ABCD呢?如图,在四边形ABCD中,DP、CP分别平分ADC和BCD,请你利用上述结论探究P与A+B的数量关系,并说明理由;
问题2:若将上题中的四边形ABCD改为六边形ABC-DEF呢?如图所示,请你利用上述结论探究P与A+B+E+F的数量关系,并说明理由.
参考答案
1.【答案】C
2.【答案】C
3.【答案】A
4.【答案】A
5.【答案】A
6.【答案】D
7.【答案】B
8.【答案】C
9.【答案】C
10.【答案】
11.【答案】
12.【答案】3,6
13.【答案】
14.【答案】解:(1)设1的邻补角为5,2的邻补角为6.
3,4,5,6是四边形的四个内角,
3+4+5+6=.
3+4=-(5+6).
1+5=,2+6=,
1+2=-(5+6).
1+2=3+4.
(2)在一个四边形中,两个外角的和等于与它们不相邻的两个内角的和.
(3)B+C=,
MDA+NAD=.
AE,DE分别是NAD,MDA的平分线,
ADE=MDA,DAE= NAD.
ADE+DAE=(MDA+ NAD)=.
E=-(ADE+DAE)= .
15.【答案】解:问题1:P=(A+B).
理由:DP、CP分别平分ADC和BCD,
PDC=ADC,PCD=BCD,
P=-PDC-PCD
=-ADC-BCD
=-(ADC+BCD)
=-(-A-B)
=(A+B).
问题2:P=(A+B+E+F)-.
理由:六边形ABCDEF的内角和为(6-2)=,
DP、CP分别平分EDC和BCD,
PDC= EDC,PCD=BCD,
P = -PDC-PCD
=-EDC-BCD
=-(EDC+BCD)
= - (- A- B- E- F)
= (A + B + E + F)- .
第5页,共6页
