2021--2022学年人教版九年级数学上册22.1二次函数的图像和性质同步习题
文档属性
| 名称 | 2021--2022学年人教版九年级数学上册22.1二次函数的图像和性质同步习题 |  | |
| 格式 | docx | ||
| 文件大小 | 493.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 18:07:46 | ||
图片预览


文档简介
22.1二次函数的图像和性质---2021--2022学年人教版(2012)九年级上学期
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.下列函数中不属于二次函数的是( )
A. B.
C. D.
2.如果是关于x的二次函数,则m的取值范围是( )
A. B. C.且 D.全体实数
3.若二次函数y=ax2+1的图象经过点(-2,0),则关于x的方程a(x-2)2+1=0的实数根为( )
A., B.,
C., D.,
4.苹果熟了,从树上落下所经过的路线s与下落的时间t满足s=(g是不为0的常数),则s与t的函数图象大致是( )
A. B. C. D.
5.函数y=ax2(a≠0)的图象经过点(a,8),则a的值为()
A.±2 B.-2 C.2 D.3
6.抛物线y=2x2﹣4的顶点坐标是( )
A.(1,﹣2) B.(0,﹣2) C.(1,﹣3) D.(0,﹣4)
7.某车的刹车距离y(m)与开始刹车时的速度x(m/s)之间满足二次函数(x>0),若该车某次的刹车距离为5 m,则开始刹车时的速度为( )
A.40 m/s B.20 m/s
C.10 m/s D.5 m/s
8.抛物线的顶点坐标是( )
A.(3,-5) B.(-3,5) C.(3,5) D.(-3,-5)
9.对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )
A.开口向下 B.对称轴是x=-1 C.顶点坐标是(1,2) D.与x轴有两个交点
10.要得到抛物线,可以将抛物线 ( ).
A.向左平移4个单位长度,再向下平移1个单位长度
B.向右平移4个单位长度,再向下平移1个单位长度
C.向左平移4个单位长度,再向上平移1个单位长度
D.向右平移4个单位长度,再向上平移1个单位长度
11.若二次函数y=-x2+bx+c中函数v与自变量x之间的部分对应值如下表
点A(x1,y1)、点B(x2,y2)在该函数图象上,当0<x1<1,2<x2<3,y1与y2的大小关系是( )
A.y1<y2 B.y1>y2 C.y1≤y2 D.y1≥y2
12.将二次函数化成的形式为( )
A. B.
C. D.
13.二次函数,当时,则( )
A. B. C. D.
14.抛物线的图像如图所示,则下列说法中:①;②;③方程没有实数根;④(为任意实数),正确的有( )个
A.1个 B.2个 C.3个 D.4个
评卷人得分
二、填空题
15.将的图像先向左平移2个单位,再向下平移5个单位,则最终所得的函数图像表达式为________.
16.如果点与点在抛物线(,,是常数,)上,那么该抛物线的对称轴为直线__________.
17.已知二次函数的图象经过(0,0),(1,2),(-1,-4)三点,那么这个二次函数的解析式是__________.
18.某商店从厂家以每件元的价格购进一批商品,该商店可以自行定价,若每件商品的售价为元,则可卖出件,那么卖出商品所赚钱元与售价元之间的函数关系为________.
评卷人得分
三、解答题
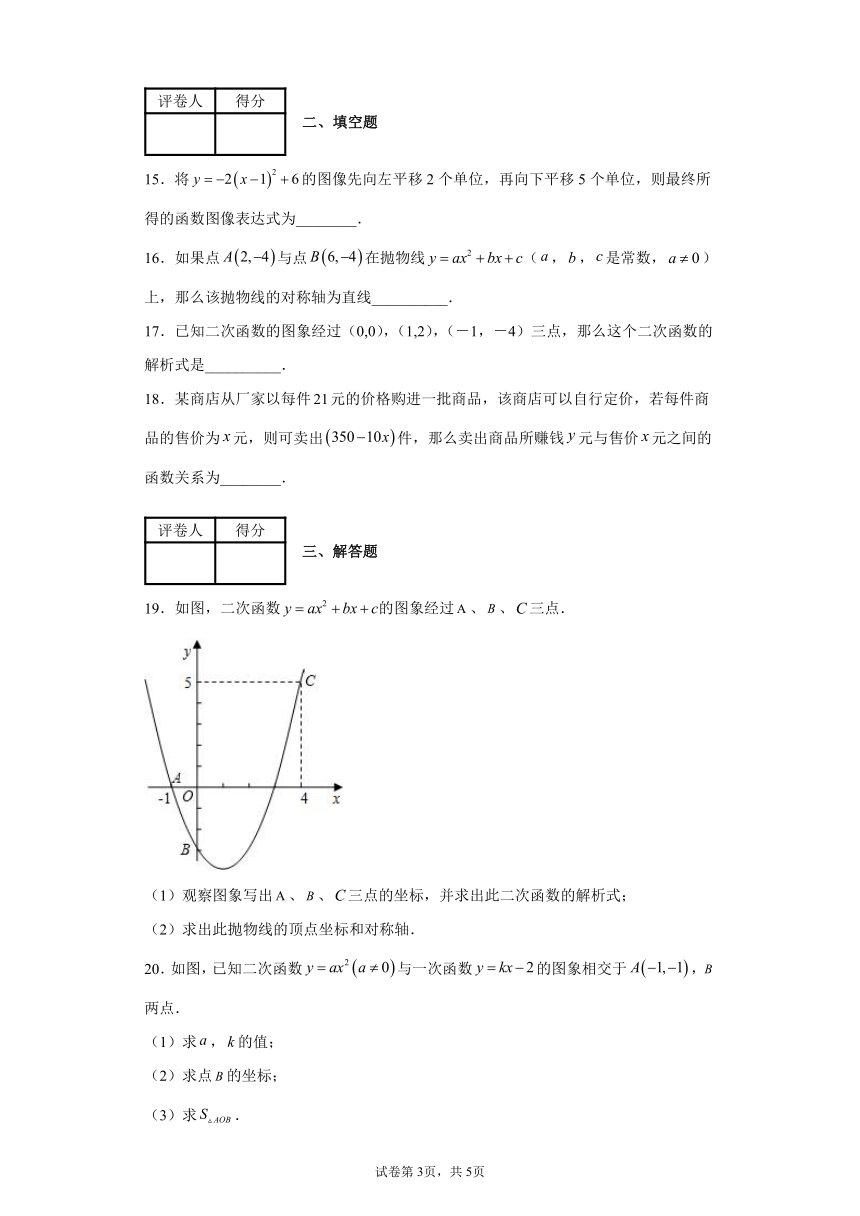
19.如图,二次函数的图象经过、、三点.
(1)观察图象写出、、三点的坐标,并求出此二次函数的解析式;
(2)求出此抛物线的顶点坐标和对称轴.
20.如图,已知二次函数与一次函数的图象相交于,两点.
(1)求,的值;
(2)求点的坐标;
(3)求.
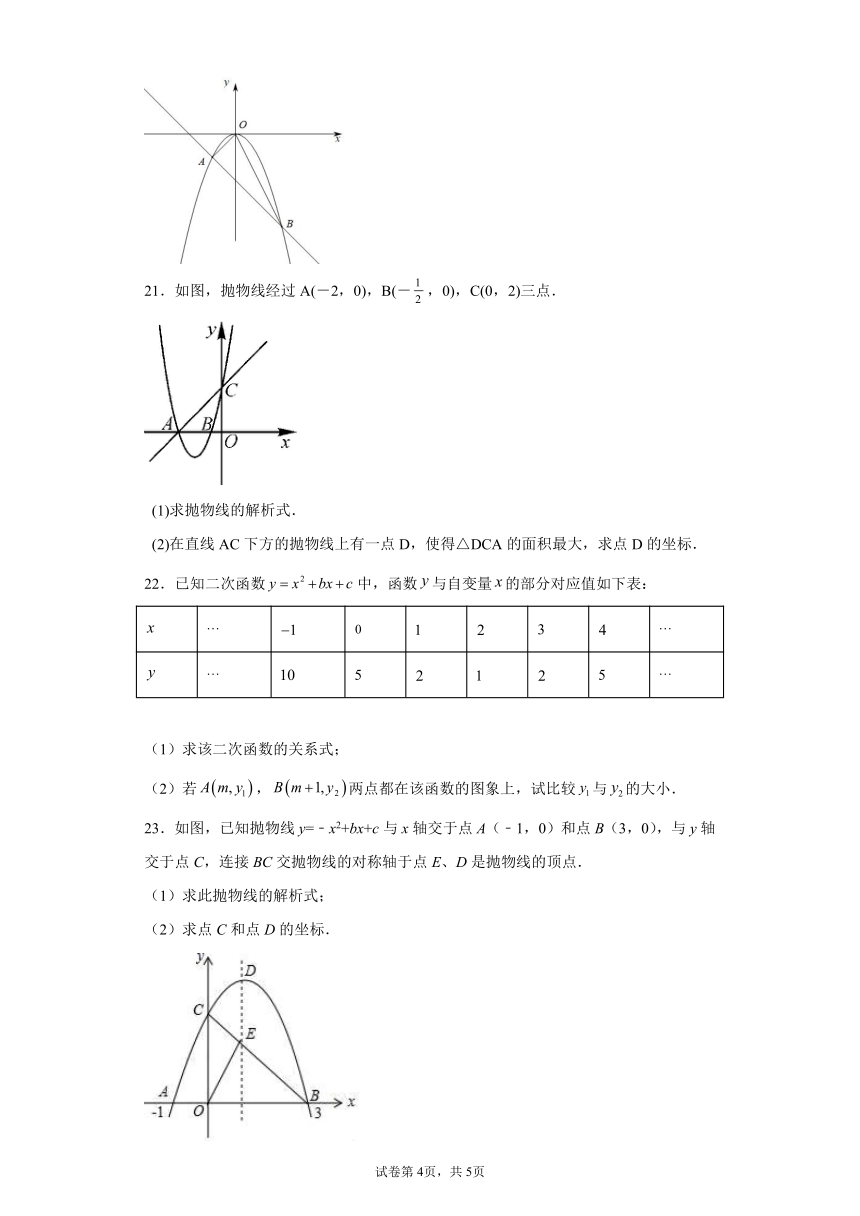
21.如图,抛物线经过A(-2,0),B(-,0),C(0,2)三点.
(1)求抛物线的解析式.
(2)在直线AC下方的抛物线上有一点D,使得△DCA的面积最大,求点D的坐标.
22.已知二次函数中,函数与自变量的部分对应值如下表:
(1)求该二次函数的关系式;
(2)若,两点都在该函数的图象上,试比较与的大小.
23.如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E、D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)求点C和点D的坐标.
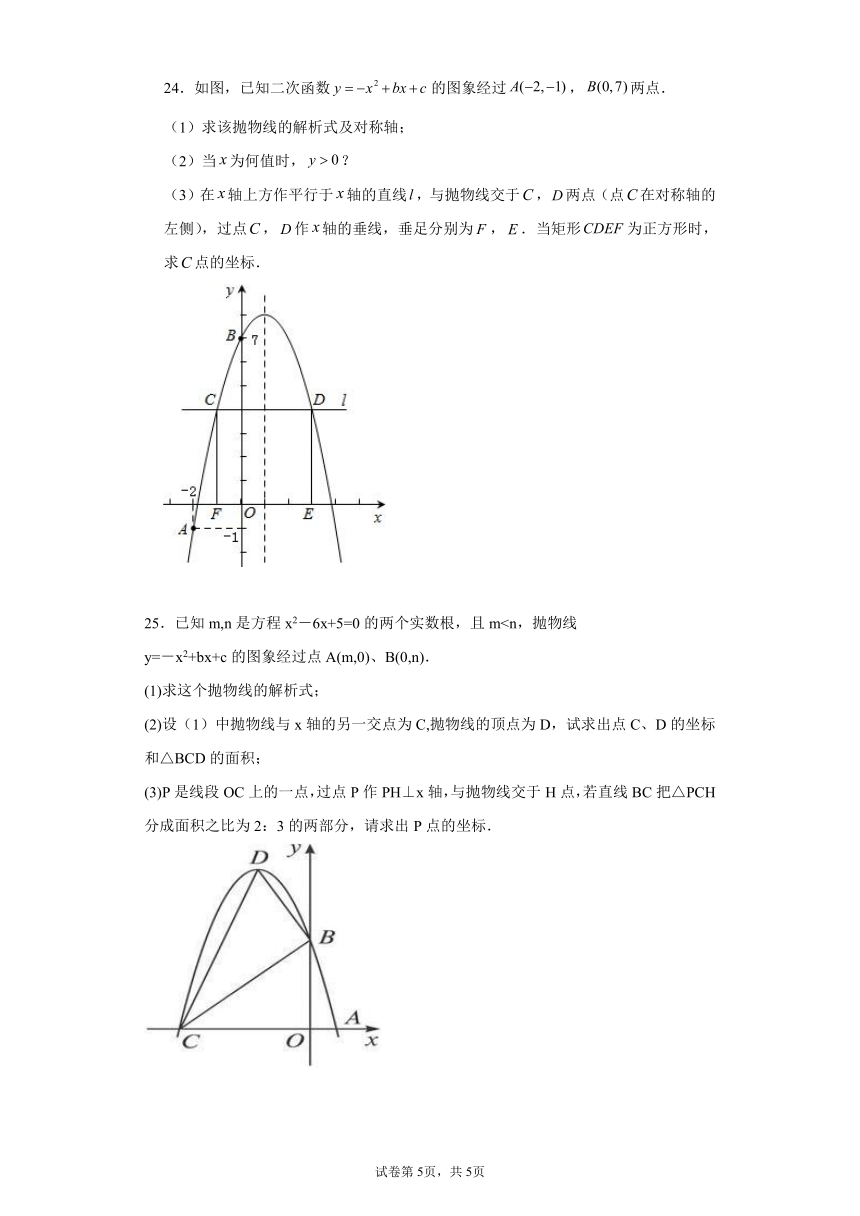
24.如图,已知二次函数的图象经过,两点.
(1)求该抛物线的解析式及对称轴;
(2)当为何值时,?
(3)在轴上方作平行于轴的直线,与抛物线交于,两点(点在对称轴的左侧),过点,作轴的垂线,垂足分别为,.当矩形为正方形时,求点的坐标.
25.已知m,n是方程x2-6x+5=0的两个实数根,且my=-x2+bx+c的图象经过点A(m,0)、B(0,n).
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;
(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
解:A、y=(x+1)(x﹣2)是二次函数,故此选项不合题意;
B、是二次函数,故此选项不合题意;
C、y=2(x+2)2﹣2x2=8x+8不是二次函数,故此选项符合题意;
D、y=1﹣x2是二次函数,故此选项不合题意;
故选:C.
2.A
解:∵是关于x的二次函数,
∴m-2≠0,即m≠2,
故选A.
3.A
解:∵二次函数y=ax2+1的图象经过点(-2,0),
∴4a+1=0,
∴a=-,
∴方程a(x-2)2+1=0为:方程-(x-2)2+1=0,
解得:x1=0,x2=4,
故选:A.
4.B
解:由
可得:是的二次函数,且函数图像经过原点,图像的开口向上,
所以:错误,正确,错误,
故选:
5.C
【解析】
把点(a,8)代入:y=ax2得:a3=8,解得:a=2.
故选C.
6.D
解:抛物线y=x2﹣4的顶点坐标为(0,﹣4).
故选D.
7.C
【解】
当y=5时,则,解之得(负值舍去),故选C
8.C
解:已知抛物,
则抛物线的顶点坐标是 (3,5);
故选:C.
9.C
解:二次函数y=(x-1)2+2的图象开口向上,顶点坐标为(1,2),对称轴为直线x=1,抛物线与x轴没有公共点.
故选:C.
10.B
解:∵y=2(x-4)2-1的顶点坐标为(4,-1),y=2x2的顶点坐标为(0,0),
∴将抛物线y=2x2向右平移4个单位,再向下平移1个单位,可得到抛物线y=2(x-4)2-1.
故选:B.
11.A
解:根据图表知,当x=1和x=3时,所对应的y值都是2,
∴抛物线的对称轴是直线x=2,
∵a=-1,
∴该二次函数的图象的开口方向是向下;
∵0<x1<1,2<x2<3,
∴A点离对称轴的距离大于B点离对称轴的距离,
∴y1<y2.
故选:A.
12.C
【解】
故选:C.
13.D
【解】
∵=,
∴当x=1时,y有最大值5;
当x=-1时,y==1;
当x=2时,y==4;
∴当时,;
故选D.
14.B
解:∵=-1,
∴b=2a,∴2a-b=0.故①错误;
∵x=1时,y<0,
∴a+b+c<0,
∴a+2a+c<0,即3a+c<0,
∵抛物线开口向下,
∴a<0,
∴b<0,
∴3a+2b+c<0,所以②正确;
∵
∴
∴
∵<2
∴无解.
即方程没有实数根;
故③正确;
∵当x=-1时,,
∴,
∴,
∴,
故④错误.
故选B.
15.y=-2(x+1)2+1y=2x2+4x+3
解:y=-2(x-1)2+6的图象先向左平移2个单位,再向下平移5个单位,则最终所得图象的函数表达式为y=-2(x-1+2)2+6-5,即y=-2(x+1)2+1.
故答案是:y=-2(x+1)2+1.
16.x=4
解:∵点A(2,-4)与点B(6,-4)的纵坐标相等,
∴点A、B关于抛物线对称轴对称,
∴抛物线的对称轴为直线x==4.
故答案为:x=4.
17.y=" -" x2+3x
【解】
:设y=ax2+bx+c,把点(0,0),(1,2),(-1,-4)代入可得:,解得,所以y= -x2+3x.
18.
解:由题意得:每件商品的盈利为:元,
所以:
故答案为:
19.解:(1)根据二次函数的图象可知:,,,
把,,代入可得,
解得,
即二次函数的解析式为.
(2)化为顶点式为;
抛物线的顶点坐标为,对称轴为直线.
20.【解】
(1)二次函数与一次函数的图象相交于,
则,解得
,解得
二次函数解析式为:
一次函数解析式为:
(2)由题意可知,已知二次函数与一次函数的图象相交于,两点
联立
解得
(3)设直线与轴的交点为,如图,
由,令,解得
,
21.【解】
(1) ∵该抛物线过点C(0,2),
∴设抛物线解析式为y=ax2+bx+2.
将A(-2,0),B(-,0)代入,得
解得
∴设该抛物线的解析式为y=2x2+5x+2.
(2) 设直线AC的解析式为y=kx+b
将A(-2,0),B(0,2)代入得
∴直线AC的解析式为y=x+2.
设D点的横坐标为t(-2<t<0),则D点的纵坐标为2t2+5t+2.
过D作y轴的平行线交AC于E,则E点的坐标为(t,t+2).
∴DE=(t+2)-(2t2+5t+2)=-2t2-4t,
用h表示点C到线段DE所在直线的距离,
∴S△DCA=S△CDE+S△ADE
=DE·h+DE·(2-h)
=DE·2
=-2t2-4t
=-2(t+1)2+2.
∵-2<t<0,
∴当t=-1时,△DCA面积最大,此时点D的坐标为(-1,-1).
22.【解】根据题意,当时,;当时,;
解得:,该二次函数关系式为;
(2),两点都在函数的图象上,
,
,
①当,即时,;
②当,即时,;
③当,即时,.
23.【解】(1)由点A(﹣1,0)和点B(3,0)得
,
解得:,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)对于抛物线y=﹣x2+2x+3,令x=0,得到y=3,
∴C(0,3),
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D(1,4).
24.解:(1)二次函数的图象经过,两点.
,
解得:,
,
,
,
,
对称轴为:直线.
(2)当,
,
,
,,
抛物线与轴交点坐标为:,,,,
当时,;
(3)当矩形为正方形时,
假设点坐标为,
点坐标为,,
即:,,
对称轴为:直线,到对称轴距离等于到对称轴距离相等,
,
解得:,(不合题意舍去),
时,,
点坐标为:.
25.解析:(1)、解方程x2-6x+5=0,得x1=5,x2=1.由m所以点A、B的坐标分别为A(1,0),B(0,5).将A(1,0),B(0,5)的坐标分别代入y=-x2+bx+c,
得解这个方程组得
所以,抛物线的解析式为y=-x2-4x+5.
(2)、由y=-x2-4x+5,令y=0,得-x2-4x+5=0,解这个方程得x1=-5,x2=1,
所以C点的坐标为(-5,0).由顶点坐标公式计算得点D(-2,9).
过D作x轴的垂线交x轴于M.则S△DMC=×9×(5-2)=,
S梯形MDBO=×2×(9+5)=14,S△BOC=×5×5=,
所以,S△BCD=S梯形MDBO+S△DMC-S△BOC=14+-=15.
(3)、设P点的坐标为(a,0),
因为线段BC过B、C两点,所以BC所在的直线方程为y=x+5.
那么,PH与直线BC的交点坐标为E(a,a+5),
PH与抛物线y=-x2-4x+5的交点坐标为H(a,-a2-4a+5).
由题意,得①EH=EP,即(-a2-4a+5)-(a+5)=(a+5).
解这个方程,得a=-或a=-5(舍去).
②EH=EP,即(-a2-4a+5)-(a+5)=(a+5),
解这个方程,得a=-或a=-5(舍去),
∴P点的坐标为(-,0)或(-,0).
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.下列函数中不属于二次函数的是( )
A. B.
C. D.
2.如果是关于x的二次函数,则m的取值范围是( )
A. B. C.且 D.全体实数
3.若二次函数y=ax2+1的图象经过点(-2,0),则关于x的方程a(x-2)2+1=0的实数根为( )
A., B.,
C., D.,
4.苹果熟了,从树上落下所经过的路线s与下落的时间t满足s=(g是不为0的常数),则s与t的函数图象大致是( )
A. B. C. D.
5.函数y=ax2(a≠0)的图象经过点(a,8),则a的值为()
A.±2 B.-2 C.2 D.3
6.抛物线y=2x2﹣4的顶点坐标是( )
A.(1,﹣2) B.(0,﹣2) C.(1,﹣3) D.(0,﹣4)
7.某车的刹车距离y(m)与开始刹车时的速度x(m/s)之间满足二次函数(x>0),若该车某次的刹车距离为5 m,则开始刹车时的速度为( )
A.40 m/s B.20 m/s
C.10 m/s D.5 m/s
8.抛物线的顶点坐标是( )
A.(3,-5) B.(-3,5) C.(3,5) D.(-3,-5)
9.对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )
A.开口向下 B.对称轴是x=-1 C.顶点坐标是(1,2) D.与x轴有两个交点
10.要得到抛物线,可以将抛物线 ( ).
A.向左平移4个单位长度,再向下平移1个单位长度
B.向右平移4个单位长度,再向下平移1个单位长度
C.向左平移4个单位长度,再向上平移1个单位长度
D.向右平移4个单位长度,再向上平移1个单位长度
11.若二次函数y=-x2+bx+c中函数v与自变量x之间的部分对应值如下表
点A(x1,y1)、点B(x2,y2)在该函数图象上,当0<x1<1,2<x2<3,y1与y2的大小关系是( )
A.y1<y2 B.y1>y2 C.y1≤y2 D.y1≥y2
12.将二次函数化成的形式为( )
A. B.
C. D.
13.二次函数,当时,则( )
A. B. C. D.
14.抛物线的图像如图所示,则下列说法中:①;②;③方程没有实数根;④(为任意实数),正确的有( )个
A.1个 B.2个 C.3个 D.4个
评卷人得分
二、填空题
15.将的图像先向左平移2个单位,再向下平移5个单位,则最终所得的函数图像表达式为________.
16.如果点与点在抛物线(,,是常数,)上,那么该抛物线的对称轴为直线__________.
17.已知二次函数的图象经过(0,0),(1,2),(-1,-4)三点,那么这个二次函数的解析式是__________.
18.某商店从厂家以每件元的价格购进一批商品,该商店可以自行定价,若每件商品的售价为元,则可卖出件,那么卖出商品所赚钱元与售价元之间的函数关系为________.
评卷人得分
三、解答题
19.如图,二次函数的图象经过、、三点.
(1)观察图象写出、、三点的坐标,并求出此二次函数的解析式;
(2)求出此抛物线的顶点坐标和对称轴.
20.如图,已知二次函数与一次函数的图象相交于,两点.
(1)求,的值;
(2)求点的坐标;
(3)求.
21.如图,抛物线经过A(-2,0),B(-,0),C(0,2)三点.
(1)求抛物线的解析式.
(2)在直线AC下方的抛物线上有一点D,使得△DCA的面积最大,求点D的坐标.
22.已知二次函数中,函数与自变量的部分对应值如下表:
(1)求该二次函数的关系式;
(2)若,两点都在该函数的图象上,试比较与的大小.
23.如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E、D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)求点C和点D的坐标.
24.如图,已知二次函数的图象经过,两点.
(1)求该抛物线的解析式及对称轴;
(2)当为何值时,?
(3)在轴上方作平行于轴的直线,与抛物线交于,两点(点在对称轴的左侧),过点,作轴的垂线,垂足分别为,.当矩形为正方形时,求点的坐标.
25.已知m,n是方程x2-6x+5=0的两个实数根,且m
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;
(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
解:A、y=(x+1)(x﹣2)是二次函数,故此选项不合题意;
B、是二次函数,故此选项不合题意;
C、y=2(x+2)2﹣2x2=8x+8不是二次函数,故此选项符合题意;
D、y=1﹣x2是二次函数,故此选项不合题意;
故选:C.
2.A
解:∵是关于x的二次函数,
∴m-2≠0,即m≠2,
故选A.
3.A
解:∵二次函数y=ax2+1的图象经过点(-2,0),
∴4a+1=0,
∴a=-,
∴方程a(x-2)2+1=0为:方程-(x-2)2+1=0,
解得:x1=0,x2=4,
故选:A.
4.B
解:由
可得:是的二次函数,且函数图像经过原点,图像的开口向上,
所以:错误,正确,错误,
故选:
5.C
【解析】
把点(a,8)代入:y=ax2得:a3=8,解得:a=2.
故选C.
6.D
解:抛物线y=x2﹣4的顶点坐标为(0,﹣4).
故选D.
7.C
【解】
当y=5时,则,解之得(负值舍去),故选C
8.C
解:已知抛物,
则抛物线的顶点坐标是 (3,5);
故选:C.
9.C
解:二次函数y=(x-1)2+2的图象开口向上,顶点坐标为(1,2),对称轴为直线x=1,抛物线与x轴没有公共点.
故选:C.
10.B
解:∵y=2(x-4)2-1的顶点坐标为(4,-1),y=2x2的顶点坐标为(0,0),
∴将抛物线y=2x2向右平移4个单位,再向下平移1个单位,可得到抛物线y=2(x-4)2-1.
故选:B.
11.A
解:根据图表知,当x=1和x=3时,所对应的y值都是2,
∴抛物线的对称轴是直线x=2,
∵a=-1,
∴该二次函数的图象的开口方向是向下;
∵0<x1<1,2<x2<3,
∴A点离对称轴的距离大于B点离对称轴的距离,
∴y1<y2.
故选:A.
12.C
【解】
故选:C.
13.D
【解】
∵=,
∴当x=1时,y有最大值5;
当x=-1时,y==1;
当x=2时,y==4;
∴当时,;
故选D.
14.B
解:∵=-1,
∴b=2a,∴2a-b=0.故①错误;
∵x=1时,y<0,
∴a+b+c<0,
∴a+2a+c<0,即3a+c<0,
∵抛物线开口向下,
∴a<0,
∴b<0,
∴3a+2b+c<0,所以②正确;
∵
∴
∴
∵<2
∴无解.
即方程没有实数根;
故③正确;
∵当x=-1时,,
∴,
∴,
∴,
故④错误.
故选B.
15.y=-2(x+1)2+1y=2x2+4x+3
解:y=-2(x-1)2+6的图象先向左平移2个单位,再向下平移5个单位,则最终所得图象的函数表达式为y=-2(x-1+2)2+6-5,即y=-2(x+1)2+1.
故答案是:y=-2(x+1)2+1.
16.x=4
解:∵点A(2,-4)与点B(6,-4)的纵坐标相等,
∴点A、B关于抛物线对称轴对称,
∴抛物线的对称轴为直线x==4.
故答案为:x=4.
17.y=" -" x2+3x
【解】
:设y=ax2+bx+c,把点(0,0),(1,2),(-1,-4)代入可得:,解得,所以y= -x2+3x.
18.
解:由题意得:每件商品的盈利为:元,
所以:
故答案为:
19.解:(1)根据二次函数的图象可知:,,,
把,,代入可得,
解得,
即二次函数的解析式为.
(2)化为顶点式为;
抛物线的顶点坐标为,对称轴为直线.
20.【解】
(1)二次函数与一次函数的图象相交于,
则,解得
,解得
二次函数解析式为:
一次函数解析式为:
(2)由题意可知,已知二次函数与一次函数的图象相交于,两点
联立
解得
(3)设直线与轴的交点为,如图,
由,令,解得
,
21.【解】
(1) ∵该抛物线过点C(0,2),
∴设抛物线解析式为y=ax2+bx+2.
将A(-2,0),B(-,0)代入,得
解得
∴设该抛物线的解析式为y=2x2+5x+2.
(2) 设直线AC的解析式为y=kx+b
将A(-2,0),B(0,2)代入得
∴直线AC的解析式为y=x+2.
设D点的横坐标为t(-2<t<0),则D点的纵坐标为2t2+5t+2.
过D作y轴的平行线交AC于E,则E点的坐标为(t,t+2).
∴DE=(t+2)-(2t2+5t+2)=-2t2-4t,
用h表示点C到线段DE所在直线的距离,
∴S△DCA=S△CDE+S△ADE
=DE·h+DE·(2-h)
=DE·2
=-2t2-4t
=-2(t+1)2+2.
∵-2<t<0,
∴当t=-1时,△DCA面积最大,此时点D的坐标为(-1,-1).
22.【解】根据题意,当时,;当时,;
解得:,该二次函数关系式为;
(2),两点都在函数的图象上,
,
,
①当,即时,;
②当,即时,;
③当,即时,.
23.【解】(1)由点A(﹣1,0)和点B(3,0)得
,
解得:,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)对于抛物线y=﹣x2+2x+3,令x=0,得到y=3,
∴C(0,3),
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D(1,4).
24.解:(1)二次函数的图象经过,两点.
,
解得:,
,
,
,
,
对称轴为:直线.
(2)当,
,
,
,,
抛物线与轴交点坐标为:,,,,
当时,;
(3)当矩形为正方形时,
假设点坐标为,
点坐标为,,
即:,,
对称轴为:直线,到对称轴距离等于到对称轴距离相等,
,
解得:,(不合题意舍去),
时,,
点坐标为:.
25.解析:(1)、解方程x2-6x+5=0,得x1=5,x2=1.由m
得解这个方程组得
所以,抛物线的解析式为y=-x2-4x+5.
(2)、由y=-x2-4x+5,令y=0,得-x2-4x+5=0,解这个方程得x1=-5,x2=1,
所以C点的坐标为(-5,0).由顶点坐标公式计算得点D(-2,9).
过D作x轴的垂线交x轴于M.则S△DMC=×9×(5-2)=,
S梯形MDBO=×2×(9+5)=14,S△BOC=×5×5=,
所以,S△BCD=S梯形MDBO+S△DMC-S△BOC=14+-=15.
(3)、设P点的坐标为(a,0),
因为线段BC过B、C两点,所以BC所在的直线方程为y=x+5.
那么,PH与直线BC的交点坐标为E(a,a+5),
PH与抛物线y=-x2-4x+5的交点坐标为H(a,-a2-4a+5).
由题意,得①EH=EP,即(-a2-4a+5)-(a+5)=(a+5).
解这个方程,得a=-或a=-5(舍去).
②EH=EP,即(-a2-4a+5)-(a+5)=(a+5),
解这个方程,得a=-或a=-5(舍去),
∴P点的坐标为(-,0)或(-,0).
同课章节目录
