2021-2022学年人教版九年级上册第二十三章旋转单元试卷(word解析版)
文档属性
| 名称 | 2021-2022学年人教版九年级上册第二十三章旋转单元试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 546.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 18:21:55 | ||
图片预览


文档简介
2021-2022学年人教版九年级上册第二十三章试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题(共24分)
1.(本题3分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A.B. C.D.
2.(本题3分)如图,将三角尺ABC(,)绕点B按顺时针方向转动一个角度到的位置,若点A、B、C’在同一条直线上,那么旋转的角度可以是( )
A. B. C. D.
3.(本题3分)在平面直角坐标系中,点关于原点对称的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(本题3分)如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是( )
A.把△ABC绕点C逆时针方向旋转90°,再向下平移2格
B.把△ABC绕点C顺时针方向旋转90°,再向下平移5格
C.把△ABC向下平移4格,再绕点C逆时针方向旋转180°
D.把△ABC向下平移5格,再绕点C顺时针方向旋转180°
5.(本题3分)如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是( )
A.50° B.60° C.40° D.30°
6.(本题3分)如图,已知点O(0,0),P(1,2),将线段PO绕点P按顺时针方向以每秒90°的速度旋转,则第19秒时,点O的对应点坐标为( )
A.(0,0) B.(3,1) C.(﹣1,3) D.(2,4)
7.(本题3分)如图,若正六边形绕着中心点旋转度后得到的图形与原来图形重合,则的最小值为( )
A. B. C. D.
8.(本题3分)己知点,将点绕原点顺时针旋转后的对应点为,将点绕原点顺时针旋转后的对应点为,依此作法继续下去,则点的坐标是( )
A. B. C. D.
二、填空题(共24分)
9.(本题3分)在平面直角坐标系中,点P(-5,3)关于原点对称点P′的坐标是________.
10.(本题3分)如图,大圆的面积为4π,大圆的两条直径互相垂直,则图中阴影部分的面积的和为_____.
11.(本题3分)已知M(a,﹣3)和N(4,b)关于原点对称,则(a+b)2002=_____.
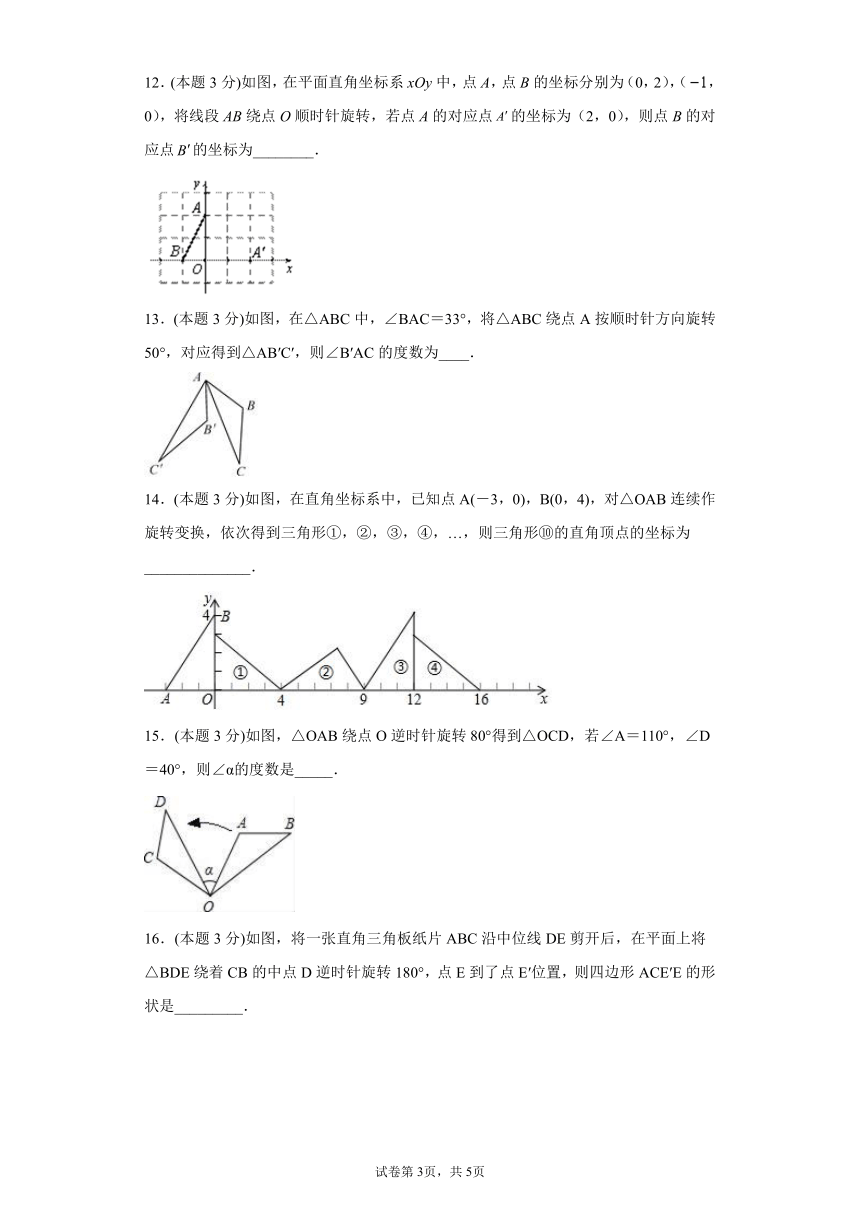
12.(本题3分)如图,在平面直角坐标系xOy中,点A,点B的坐标分别为(0,2),(,0),将线段AB绕点O顺时针旋转,若点A的对应点的坐标为(2,0),则点B的对应点的坐标为________.
13.(本题3分)如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为____.
14.(本题3分)如图,在直角坐标系中,已知点A(-3,0),B(0,4),对△OAB连续作旋转变换,依次得到三角形①,②,③,④,…,则三角形⑩的直角顶点的坐标为______________.
15.(本题3分)如图,△OAB绕点O逆时针旋转80°得到△OCD,若∠A=110°,∠D=40°,则∠α的度数是_____.
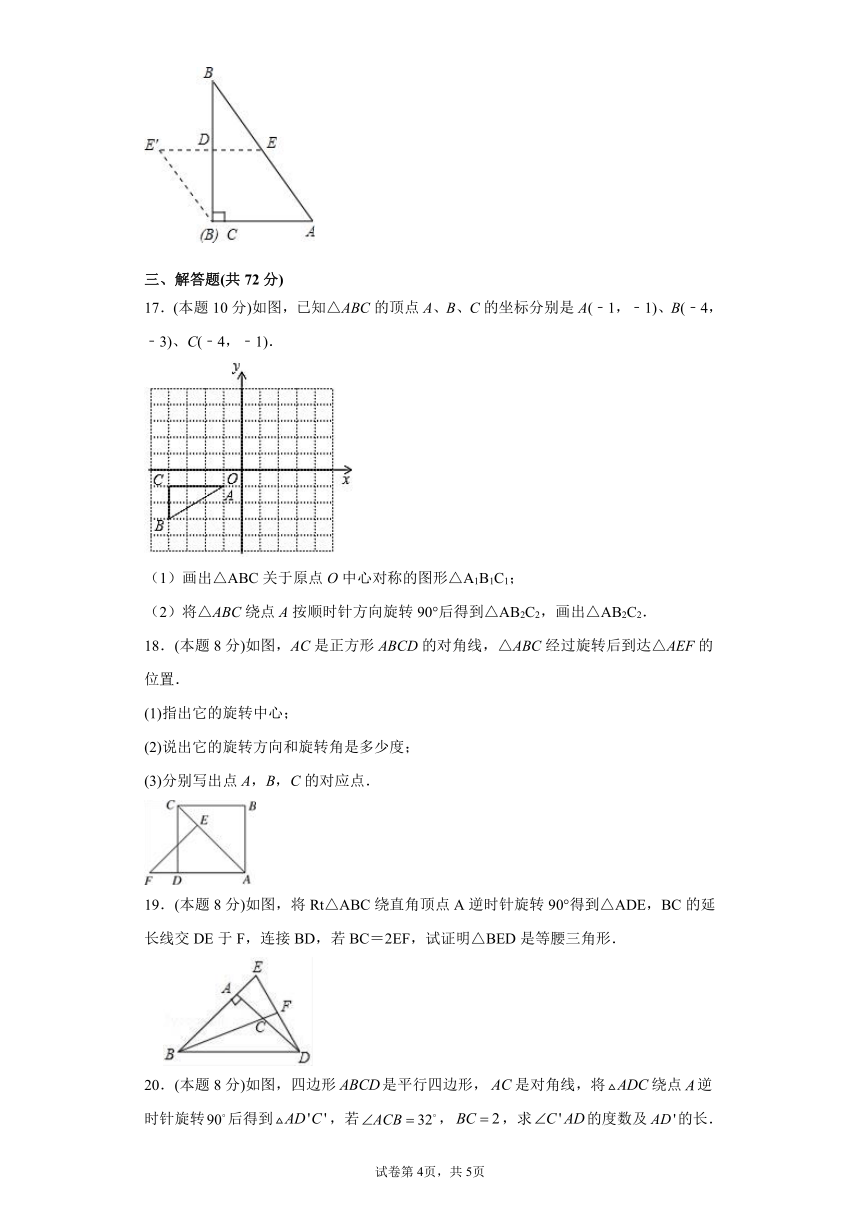
16.(本题3分)如图,将一张直角三角板纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置,则四边形ACE′E的形状是_________.
三、解答题(共72分)
17.(本题10分)如图,已知△ABC的顶点A、B、C的坐标分别是A(﹣1,﹣1)、B(﹣4,﹣3)、C(﹣4,﹣1).
(1)画出△ABC关于原点O中心对称的图形△A1B1C1;
(2)将△ABC绕点A按顺时针方向旋转90°后得到△AB2C2,画出△AB2C2.
18.(本题8分)如图,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置.
(1)指出它的旋转中心;
(2)说出它的旋转方向和旋转角是多少度;
(3)分别写出点A,B,C的对应点.
19.(本题8分)如图,将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE,BC的延长线交DE于F,连接BD,若BC=2EF,试证明△BED是等腰三角形.
20.(本题8分)如图,四边形是平行四边形,是对角线,将绕点逆时针旋转后得到,若,,求的度数及的长.
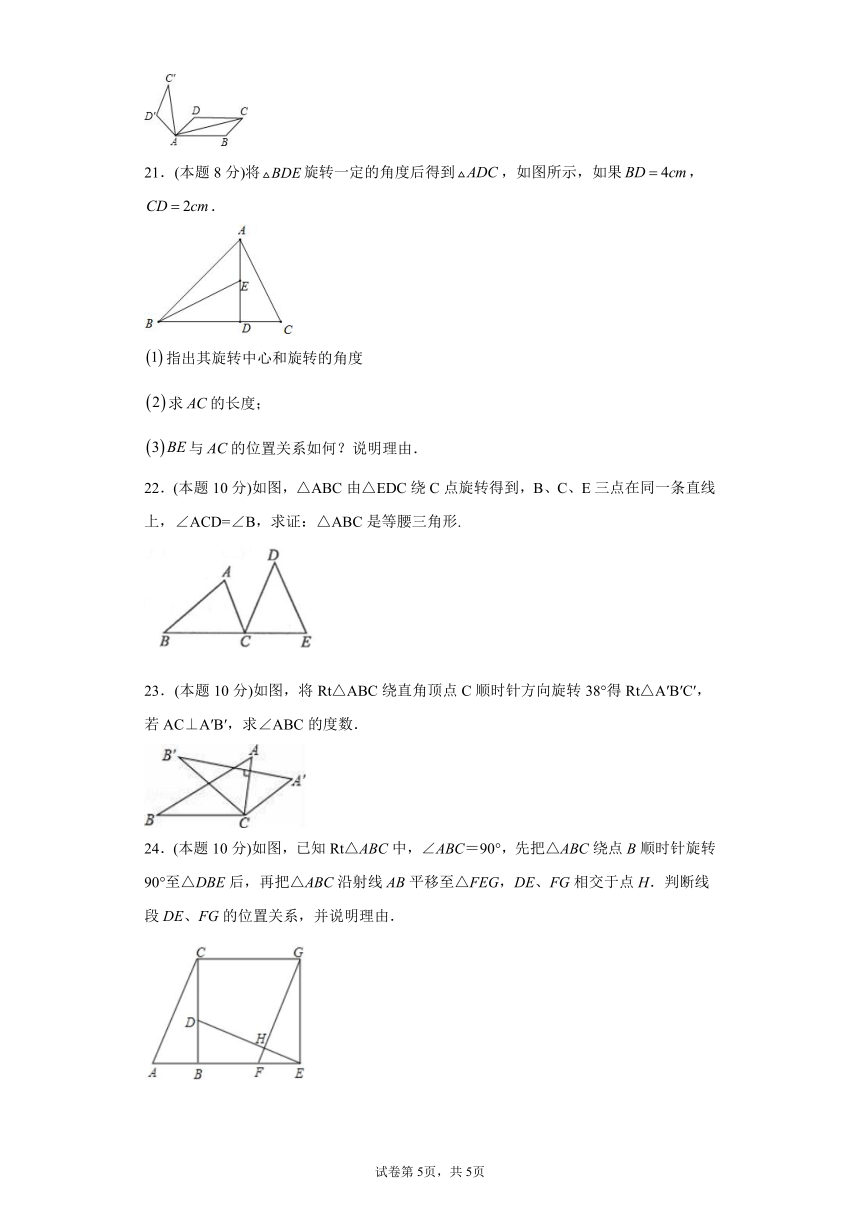
21.(本题8分)将旋转一定的角度后得到,如图所示,如果,.
指出其旋转中心和旋转的角度
求的长度;
与的位置关系如何?说明理由.
22.(本题10分)如图,△ABC由△EDC绕C点旋转得到,B、C、E三点在同一条直线上,∠ACD=∠B,求证:△ABC是等腰三角形.
23.(本题10分)如图,将Rt△ABC绕直角顶点C顺时针方向旋转38°得Rt△A′B′C′,若AC⊥A′B′,求∠ABC的度数.
24.(本题10分)如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.判断线段DE、FG的位置关系,并说明理由.
参考答案
1.B
【分析】
根据轴对称图形的定义:如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形;中心对称图形的定义:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,即可得出答案.
【详解】
解:A、是轴对称图形,不是中心对称图形,故本选项错误;
B、是轴对称图形,也是中心对称图形,故本选项正确;
C、不是轴对称图形,是中心对称图形,故本选项错误;
D、是轴对称图形,不是中心对称图形,故本选项错误;
故选B.
【点睛】
本题考查的是轴对称图形和中心对称图形的定义,熟练掌握相关定义是解决本题的关键.
2.D
【分析】
根据三角形内角和定理求出,即,明确旋转角即为即可求解.
【详解】
解:∵,,
∴,
∵点A、B、C’在同一条直线上,
∴,
∴旋转的角度可以是,
故选:D.
【点睛】
本题考查旋转的性质、三角形的内角和定理,明确旋转角即为是解题的关键.
3.D
【分析】
根据关于原点对称的点坐标变换规律即可得.
【详解】
解:点关于原点对称的点的坐标为,
在平面直角坐标系中,点关于原点对称的点在第四象限,
故选:D.
【点睛】
本题考查了关于原点对称的点坐标变换规律,熟练掌握关于原点对称的点坐标变换规律是解题关键.
4.B
【详解】
几何变换的类型.
【分析】根据图象,△ABC绕点C顺时针方向旋转90°,再向下平移5格即可与△DEF重合.故选B.
5.A
【分析】
根据旋转的性质得知∠A=∠C,∠AOC为旋转角等于80°,则可以利用三角形内角和度数为180°列出式子进行求解.
【详解】
解:∵将△OAB绕点O逆时针旋转80°
∴∠A=∠C,∠AOC=80°
∴∠DOC=80°﹣α
∵∠A=2∠D=100°
∴∠D=50°
∵∠C+∠D+∠DOC=180°
∴100°+50°+80°﹣α=180° 解得α=50°
故选:A.
【点睛】
本题主要考查了旋转的性质及三角形的内角和定理,熟知图形旋转的性质:对应点与旋转中心所连线段的夹角等于旋转角是解决本题的关键.
6.B
【分析】
依据线段PO绕点P按顺时针方向以每秒90°的速度旋转,即可得到19秒后点O旋转到点O'的位置,再根据全等三角形的对应边相等,即可得到点O的对应点O'的坐标.
【详解】
解:如图所示,∵线段PO绕点P按顺时针方向以每秒90°的速度旋转,每4秒一个循环,19=4×4+3,
∴3×90°=270°,
∴19秒后点O旋转到点O'的位置,∠OPO'=90°,
如图所示,过P作MN⊥y轴于点M,过O'作O'N⊥MN于点N,
则∠OMP=∠PNO'=90°,∠POM=∠O'PN,OP=PO',
在△OPM和△PO'N中,
,
∴△OPM≌△PO'N(AAS),
∴O'N=PM=1,PN=OM=2,
∴MN=1+2=3,点O'离x轴的距离为2-1=1,
∴点O'的坐标为(3,1),
故选:B.
【点睛】
本题主要考查了坐标与图形变化,图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.
7.D
【解析】
【分析】
先求出正六边形ABCDEF的中心角,然后根据正六边形的性质可判定正六边形ABCDEF绕着中心点O旋转60°的整数倍后得到的图形与原来图形重合.
【详解】
∵正六边形ABCDEF的中心角的度数为=60°,
∴正六边形ABCDEF绕着中心点O旋转60°的整数倍后得到的图形与原来图形重合.
故选:D.
【点睛】
本题考查了旋转对称图形:如果某一个图形围绕某一点旋转一定的角度(小于360°)后能与原图形重合,那么这个图形就叫做旋转对称图形.常见的旋转对称图形有:线段,正多边形,平行四边形,圆等.
8.B
【分析】
根据图形旋转的规律得出每旋转6次坐标一循环,求出点的坐标与点坐标相同,进而可得出答案.
【详解】
解:将点A绕原点O顺时针旋转60后的对应点为A,将点A绕原点O顺时针旋转60后的对应点为A,依此作法继续下去,
得出每旋转=6次坐标一循环,得出20126=335余2,即点A的坐标与点A坐标相同,即可得出点A与点A关于x轴对称,
A点坐标为:(1,-).
所以B选项是正确的.
【点睛】
此题主要考查了坐标与图形的旋转与规律问题,解答此题的关键是明确图形旋转的变化规律每旋转6次坐标一循环.
9.(5,-3)
【详解】
关于原点对称的点的坐标是横、纵坐标都互为相反数,
点P(-5, 3)关于原点对称点P′的坐标是(5,-3),
故答案为(5,-3).
10.π
【详解】
试题解析:由题意得:
图中阴影部分的面积正好是大圆面积的
阴影部分的面积为:
故答案为
11.1
【详解】
∵M(a,﹣3)和N(4,b)关于原点对称,
∴a=-4,b=3,
∴.
点睛:关于原点对称的两个点,横坐标与横坐标,纵坐标与纵坐标分别互为相反数.
12.(0,1)
【详解】
由图可知:的坐标为(0,1).
13.17°
【详解】
解:∵∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,
∴∠B′AC′=33°,∠BAB′=50°,
∴∠B′AC的度数=50° 33°=17°.
故答案为17°.
14.(36,0)
【分析】
先利用勾股定理求出AB的长,再求出三角形OAB的周长,再研究图形旋转的规律,每三次旋转为一个周期,相当平移一个三角形的周长12个单位,利用10除以3求余数1,说明三个循环直角回坐标轴上,第10次绕直角旋转没动即可求出.
【详解】
由点A(-3,0),B(0,4),在△AOB中由勾股定理得AB=,
三角形OAB的周长=3+4+5=12,
由原图到图③,旋转一个周期,相当于向右平移了12个单位长度,每三个图旋转一个周期直角回到坐标轴上,
10÷3=3…1,
由于⑨直角顶点到⑩位置没动,
三角形④的直角顶点的坐标为(12,0),象这样平移三次直角顶点是(12×3,0),即(36,0),
则三角形⑩的直角顶点的坐标为(36,0).
故答案为:(36,0).
【点睛】
本题考查图形旋转规律探索题涉及点的坐标,勾股定理,三角形周长,旋转与平移关系,,掌握点的坐标的求法,勾股定理的应用,会求三角形周长,会用旋转与平移关系解释旋转规律是解题关键.
15.50°
【分析】
已知旋转角为80°,即∠DOB=80°,欲求∠α的度数,必须先求出∠AOB的度数,利用三角形内角和定理求解即可.
【详解】
解:由旋转的性质知:∠A=∠C=110°,∠D=∠B=40°;
根据三角形内角和定理知:∠AOB=180°﹣110°﹣40°=30°;
已知旋转角∠DOB=80°,则∠α=∠DOB﹣∠AOB=50°.
故答案为50°.
【点睛】
此题主要考查的是旋转的性质,同时还涉及到三角形内角和定理的运用,难度不大.
16.平行四边形.
【分析】
四边形ACE′E的形状是平行四边形;首先根据三角形中位线的性质可得DE∥AC,DE=AC,再根据旋转可得DE=DE′,然后可根据一组对边平行且相等的四边形是平行四边形进行判定即可.
【详解】
解:∵DE是△ABC的中位线
∴DE∥AC,DE=AC
∵将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E'位置
∴DE=DE'
∴EE'=2DE=AC
∴四边形ACE'E是平行四边形.
故答案为:平行四边形.
17.(1)见详解,(2)见详解.
【分析】
(1)分别作出A,B,C的对应点A1,B1,C1即可.
(2)分别作出B,C的对应点B2,C2即可.
【详解】
解:(1)如图,分别作出A,B,C关于原点O中心对称的对应点A1,B1,C1,连接A1B1, B1C1, A1C1,△A1B1C1即为所求作的三角形;
(2)如图,分别作出B,C绕点A按顺时针方向旋转90°的对应点B2,C2,AB2, B2C2 AC2,连接△AB2C2即为所求作的三角形.
【点睛】
本题考查的是作图-旋转变换,熟知图形旋转不变性的性质是解答此题的关键.
18.(1)A;(2) 旋转方向为逆时针方向,旋转角是45度;(3) A,E,F.
【详解】
试题分析:(1)因为△ABC经过旋转后到达△AEF的位置,则A点的对应点为A,于是可判断旋转中心为点A; (2)根据旋转的性质求解; (3)根据旋转的性质求解.
解:(1)它的旋转中心为点A;
(2)它的旋转方向为逆时针方向,旋转角是45度;
(3)点A,B,C的对应点分别为点A,E,F.
19.见解析
【分析】
根据直角三角形的两锐角互余,以及对顶角相等,旋转的性质,即可证得是的垂直平分线,据此即可证得.
【详解】
证明:∵将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE,
∴DE=BC,∠ADF=∠ABC,
∵BC=2EF,
∴DF=EF,
∴DE=2EF,
∵在直角△ABC中,∠ABC+∠ACB=90°,
又∵∠ABC=∠ADE,
∴∠ACB+∠ADE=90°.
∵∠FCD=∠ACB,
∴∠FCD+∠ADE=90°,
∴∠CFD=90°,
∴BF⊥DE,
∵EF=FD,
∴BF垂直平分DE,
∴BD=BE,
∴△BDE是等腰三角形.
【点睛】
本题考查了旋转的性质、等腰三角形的判定、线段垂直平分线的判定和性质,熟练掌握各定理是解题的关键.
20.,.
【分析】
先由平行四边形的性质求出∠DAC,再由旋转的性质求出结论.
【详解】
在平行四边形ABCD中,AD∥BC,AD=BC,∴∠DAC=∠ACB=32°,由旋转的性质得∠C'AD=90°﹣∠DAC=58°,∴AD'=AD=BC=2.
【点睛】
本题是旋转的性质,主要考查了平行四边形的性质,旋转的性质,解答本题的关键是用旋转的性质得到对应边相等,对应角线段.
21.点为旋转中心,对应边、的夹角为旋转角即;;(3)、的位置关系为:.理由见解析.
【分析】
(1)根据旋转的性质,点D为旋转中心,对应边BD、AD的夹角为旋转角;
(2)根据旋转的性质可得BD=AD,然后根据勾股定理计算即可;
(3)延长BE交AC于F,根据旋转可得△BDE和△ADC全等,根据全等三角形对应角相等可得∠DBE=∠DAC,然后求出∠DAC+∠AEF=90°,判断出BE⊥AC.
【详解】
(1)由题意可知点D为旋转中心,对应边BD、AD的夹角为旋转角即90°;
(2)根据旋转的性质可得BD=AD=4cm,CD=2cm,∴AC===2cm;
(3)BE、AC的位置关系为:BE⊥AC.理由如下:
延长BE交AC于F.
∵△BDE按顺时针方向旋转一定角度后得到△ADC,∴△BDE≌△ADC,∴∠DBE=∠DAC.
∵∠DBE+∠BED=90°,∴∠DAC+∠AEF=90°,∴∠AFE=180°﹣90°=90°,∴BE⊥AC,∴BE、AC的位置关系为:BE⊥AC.
【点睛】
本题考查了旋转的性质和勾股定理的运用,旋转变化前后,对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.要注意旋转的三要素:①定点﹣旋转中心;②旋转方向;③旋转角度.
22.见解析
【分析】
由旋转的性质可知∠D=∠B,再根据已知条件证明AC∥DE,进而证明∠ACB=∠A,所以△ABC是等腰三角形.
【详解】
证明:由旋转知∠D=∠B,
∵∠ACD=∠B,
∴∠ACD=∠D,AC∥DE,
∴∠ACB=∠E,
又∵∠A=∠E,
∴∠ACB=∠A,
∴△ABC是等腰三角形.
【点睛】
本题考查了旋转的性质以及等腰三角形的判定,对于旋转的性质用到最多的是:旋转前、后的图形全等.
23.38°.
【详解】
分析:
如下图所示,设AC与A′B′的交点为O,则由已知条件易得∠A′OC=90°,∠ACA′=38°,由此可得∠A′=52°,由旋转的性质可得∠A=52°,结合∠ACB=90°即可得到∠ABC=38°.
详解:
∵Rt△ABC绕直角顶点C顺时针方向旋转38°得Rt△A′B′C′,
∴∠ACA′=38°,∠A=∠A′,
∵AC⊥A′B′,
∴∠A′OC=90°,
∴∠A′=90°-38°=52°,
∴∠A=52°,
又∵在Rt△ABC中,∠ACB=90°,
∴∠ABC=180°-90°-52°=38°.
点睛:“由旋转的性质得到∠ACA′=38°,结合AC⊥A′B′得到∠A′=52°=∠A”是解答本题的关键.
24.见解析
【分析】
根据旋转和平移可得∠DEB=∠ACB,∠GFE=∠A,再根据∠ABC=90°可得∠A+∠ACB=90°,进而得到∠DEB+∠GFE=90°,从而得到DE、FG的位置关系是垂直.
【详解】
解:DE⊥FG.
理由:由题知:Rt△ABC≌Rt△BDE≌Rt△FEG
∴∠A=∠BDE=∠GFE
∵∠BDE+∠BED=90°
∴∠GFE+∠BED=90°,即DE⊥FG.
试卷第2页,共5页
试卷第1页,共5页
学校:___________姓名:___________班级:___________考号:___________
一、单选题(共24分)
1.(本题3分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A.B. C.D.
2.(本题3分)如图,将三角尺ABC(,)绕点B按顺时针方向转动一个角度到的位置,若点A、B、C’在同一条直线上,那么旋转的角度可以是( )
A. B. C. D.
3.(本题3分)在平面直角坐标系中,点关于原点对称的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(本题3分)如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是( )
A.把△ABC绕点C逆时针方向旋转90°,再向下平移2格
B.把△ABC绕点C顺时针方向旋转90°,再向下平移5格
C.把△ABC向下平移4格,再绕点C逆时针方向旋转180°
D.把△ABC向下平移5格,再绕点C顺时针方向旋转180°
5.(本题3分)如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是( )
A.50° B.60° C.40° D.30°
6.(本题3分)如图,已知点O(0,0),P(1,2),将线段PO绕点P按顺时针方向以每秒90°的速度旋转,则第19秒时,点O的对应点坐标为( )
A.(0,0) B.(3,1) C.(﹣1,3) D.(2,4)
7.(本题3分)如图,若正六边形绕着中心点旋转度后得到的图形与原来图形重合,则的最小值为( )
A. B. C. D.
8.(本题3分)己知点,将点绕原点顺时针旋转后的对应点为,将点绕原点顺时针旋转后的对应点为,依此作法继续下去,则点的坐标是( )
A. B. C. D.
二、填空题(共24分)
9.(本题3分)在平面直角坐标系中,点P(-5,3)关于原点对称点P′的坐标是________.
10.(本题3分)如图,大圆的面积为4π,大圆的两条直径互相垂直,则图中阴影部分的面积的和为_____.
11.(本题3分)已知M(a,﹣3)和N(4,b)关于原点对称,则(a+b)2002=_____.
12.(本题3分)如图,在平面直角坐标系xOy中,点A,点B的坐标分别为(0,2),(,0),将线段AB绕点O顺时针旋转,若点A的对应点的坐标为(2,0),则点B的对应点的坐标为________.
13.(本题3分)如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为____.
14.(本题3分)如图,在直角坐标系中,已知点A(-3,0),B(0,4),对△OAB连续作旋转变换,依次得到三角形①,②,③,④,…,则三角形⑩的直角顶点的坐标为______________.
15.(本题3分)如图,△OAB绕点O逆时针旋转80°得到△OCD,若∠A=110°,∠D=40°,则∠α的度数是_____.
16.(本题3分)如图,将一张直角三角板纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置,则四边形ACE′E的形状是_________.
三、解答题(共72分)
17.(本题10分)如图,已知△ABC的顶点A、B、C的坐标分别是A(﹣1,﹣1)、B(﹣4,﹣3)、C(﹣4,﹣1).
(1)画出△ABC关于原点O中心对称的图形△A1B1C1;
(2)将△ABC绕点A按顺时针方向旋转90°后得到△AB2C2,画出△AB2C2.
18.(本题8分)如图,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置.
(1)指出它的旋转中心;
(2)说出它的旋转方向和旋转角是多少度;
(3)分别写出点A,B,C的对应点.
19.(本题8分)如图,将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE,BC的延长线交DE于F,连接BD,若BC=2EF,试证明△BED是等腰三角形.
20.(本题8分)如图,四边形是平行四边形,是对角线,将绕点逆时针旋转后得到,若,,求的度数及的长.
21.(本题8分)将旋转一定的角度后得到,如图所示,如果,.
指出其旋转中心和旋转的角度
求的长度;
与的位置关系如何?说明理由.
22.(本题10分)如图,△ABC由△EDC绕C点旋转得到,B、C、E三点在同一条直线上,∠ACD=∠B,求证:△ABC是等腰三角形.
23.(本题10分)如图,将Rt△ABC绕直角顶点C顺时针方向旋转38°得Rt△A′B′C′,若AC⊥A′B′,求∠ABC的度数.
24.(本题10分)如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.判断线段DE、FG的位置关系,并说明理由.
参考答案
1.B
【分析】
根据轴对称图形的定义:如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形;中心对称图形的定义:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,即可得出答案.
【详解】
解:A、是轴对称图形,不是中心对称图形,故本选项错误;
B、是轴对称图形,也是中心对称图形,故本选项正确;
C、不是轴对称图形,是中心对称图形,故本选项错误;
D、是轴对称图形,不是中心对称图形,故本选项错误;
故选B.
【点睛】
本题考查的是轴对称图形和中心对称图形的定义,熟练掌握相关定义是解决本题的关键.
2.D
【分析】
根据三角形内角和定理求出,即,明确旋转角即为即可求解.
【详解】
解:∵,,
∴,
∵点A、B、C’在同一条直线上,
∴,
∴旋转的角度可以是,
故选:D.
【点睛】
本题考查旋转的性质、三角形的内角和定理,明确旋转角即为是解题的关键.
3.D
【分析】
根据关于原点对称的点坐标变换规律即可得.
【详解】
解:点关于原点对称的点的坐标为,
在平面直角坐标系中,点关于原点对称的点在第四象限,
故选:D.
【点睛】
本题考查了关于原点对称的点坐标变换规律,熟练掌握关于原点对称的点坐标变换规律是解题关键.
4.B
【详解】
几何变换的类型.
【分析】根据图象,△ABC绕点C顺时针方向旋转90°,再向下平移5格即可与△DEF重合.故选B.
5.A
【分析】
根据旋转的性质得知∠A=∠C,∠AOC为旋转角等于80°,则可以利用三角形内角和度数为180°列出式子进行求解.
【详解】
解:∵将△OAB绕点O逆时针旋转80°
∴∠A=∠C,∠AOC=80°
∴∠DOC=80°﹣α
∵∠A=2∠D=100°
∴∠D=50°
∵∠C+∠D+∠DOC=180°
∴100°+50°+80°﹣α=180° 解得α=50°
故选:A.
【点睛】
本题主要考查了旋转的性质及三角形的内角和定理,熟知图形旋转的性质:对应点与旋转中心所连线段的夹角等于旋转角是解决本题的关键.
6.B
【分析】
依据线段PO绕点P按顺时针方向以每秒90°的速度旋转,即可得到19秒后点O旋转到点O'的位置,再根据全等三角形的对应边相等,即可得到点O的对应点O'的坐标.
【详解】
解:如图所示,∵线段PO绕点P按顺时针方向以每秒90°的速度旋转,每4秒一个循环,19=4×4+3,
∴3×90°=270°,
∴19秒后点O旋转到点O'的位置,∠OPO'=90°,
如图所示,过P作MN⊥y轴于点M,过O'作O'N⊥MN于点N,
则∠OMP=∠PNO'=90°,∠POM=∠O'PN,OP=PO',
在△OPM和△PO'N中,
,
∴△OPM≌△PO'N(AAS),
∴O'N=PM=1,PN=OM=2,
∴MN=1+2=3,点O'离x轴的距离为2-1=1,
∴点O'的坐标为(3,1),
故选:B.
【点睛】
本题主要考查了坐标与图形变化,图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.
7.D
【解析】
【分析】
先求出正六边形ABCDEF的中心角,然后根据正六边形的性质可判定正六边形ABCDEF绕着中心点O旋转60°的整数倍后得到的图形与原来图形重合.
【详解】
∵正六边形ABCDEF的中心角的度数为=60°,
∴正六边形ABCDEF绕着中心点O旋转60°的整数倍后得到的图形与原来图形重合.
故选:D.
【点睛】
本题考查了旋转对称图形:如果某一个图形围绕某一点旋转一定的角度(小于360°)后能与原图形重合,那么这个图形就叫做旋转对称图形.常见的旋转对称图形有:线段,正多边形,平行四边形,圆等.
8.B
【分析】
根据图形旋转的规律得出每旋转6次坐标一循环,求出点的坐标与点坐标相同,进而可得出答案.
【详解】
解:将点A绕原点O顺时针旋转60后的对应点为A,将点A绕原点O顺时针旋转60后的对应点为A,依此作法继续下去,
得出每旋转=6次坐标一循环,得出20126=335余2,即点A的坐标与点A坐标相同,即可得出点A与点A关于x轴对称,
A点坐标为:(1,-).
所以B选项是正确的.
【点睛】
此题主要考查了坐标与图形的旋转与规律问题,解答此题的关键是明确图形旋转的变化规律每旋转6次坐标一循环.
9.(5,-3)
【详解】
关于原点对称的点的坐标是横、纵坐标都互为相反数,
点P(-5, 3)关于原点对称点P′的坐标是(5,-3),
故答案为(5,-3).
10.π
【详解】
试题解析:由题意得:
图中阴影部分的面积正好是大圆面积的
阴影部分的面积为:
故答案为
11.1
【详解】
∵M(a,﹣3)和N(4,b)关于原点对称,
∴a=-4,b=3,
∴.
点睛:关于原点对称的两个点,横坐标与横坐标,纵坐标与纵坐标分别互为相反数.
12.(0,1)
【详解】
由图可知:的坐标为(0,1).
13.17°
【详解】
解:∵∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,
∴∠B′AC′=33°,∠BAB′=50°,
∴∠B′AC的度数=50° 33°=17°.
故答案为17°.
14.(36,0)
【分析】
先利用勾股定理求出AB的长,再求出三角形OAB的周长,再研究图形旋转的规律,每三次旋转为一个周期,相当平移一个三角形的周长12个单位,利用10除以3求余数1,说明三个循环直角回坐标轴上,第10次绕直角旋转没动即可求出.
【详解】
由点A(-3,0),B(0,4),在△AOB中由勾股定理得AB=,
三角形OAB的周长=3+4+5=12,
由原图到图③,旋转一个周期,相当于向右平移了12个单位长度,每三个图旋转一个周期直角回到坐标轴上,
10÷3=3…1,
由于⑨直角顶点到⑩位置没动,
三角形④的直角顶点的坐标为(12,0),象这样平移三次直角顶点是(12×3,0),即(36,0),
则三角形⑩的直角顶点的坐标为(36,0).
故答案为:(36,0).
【点睛】
本题考查图形旋转规律探索题涉及点的坐标,勾股定理,三角形周长,旋转与平移关系,,掌握点的坐标的求法,勾股定理的应用,会求三角形周长,会用旋转与平移关系解释旋转规律是解题关键.
15.50°
【分析】
已知旋转角为80°,即∠DOB=80°,欲求∠α的度数,必须先求出∠AOB的度数,利用三角形内角和定理求解即可.
【详解】
解:由旋转的性质知:∠A=∠C=110°,∠D=∠B=40°;
根据三角形内角和定理知:∠AOB=180°﹣110°﹣40°=30°;
已知旋转角∠DOB=80°,则∠α=∠DOB﹣∠AOB=50°.
故答案为50°.
【点睛】
此题主要考查的是旋转的性质,同时还涉及到三角形内角和定理的运用,难度不大.
16.平行四边形.
【分析】
四边形ACE′E的形状是平行四边形;首先根据三角形中位线的性质可得DE∥AC,DE=AC,再根据旋转可得DE=DE′,然后可根据一组对边平行且相等的四边形是平行四边形进行判定即可.
【详解】
解:∵DE是△ABC的中位线
∴DE∥AC,DE=AC
∵将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E'位置
∴DE=DE'
∴EE'=2DE=AC
∴四边形ACE'E是平行四边形.
故答案为:平行四边形.
17.(1)见详解,(2)见详解.
【分析】
(1)分别作出A,B,C的对应点A1,B1,C1即可.
(2)分别作出B,C的对应点B2,C2即可.
【详解】
解:(1)如图,分别作出A,B,C关于原点O中心对称的对应点A1,B1,C1,连接A1B1, B1C1, A1C1,△A1B1C1即为所求作的三角形;
(2)如图,分别作出B,C绕点A按顺时针方向旋转90°的对应点B2,C2,AB2, B2C2 AC2,连接△AB2C2即为所求作的三角形.
【点睛】
本题考查的是作图-旋转变换,熟知图形旋转不变性的性质是解答此题的关键.
18.(1)A;(2) 旋转方向为逆时针方向,旋转角是45度;(3) A,E,F.
【详解】
试题分析:(1)因为△ABC经过旋转后到达△AEF的位置,则A点的对应点为A,于是可判断旋转中心为点A; (2)根据旋转的性质求解; (3)根据旋转的性质求解.
解:(1)它的旋转中心为点A;
(2)它的旋转方向为逆时针方向,旋转角是45度;
(3)点A,B,C的对应点分别为点A,E,F.
19.见解析
【分析】
根据直角三角形的两锐角互余,以及对顶角相等,旋转的性质,即可证得是的垂直平分线,据此即可证得.
【详解】
证明:∵将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE,
∴DE=BC,∠ADF=∠ABC,
∵BC=2EF,
∴DF=EF,
∴DE=2EF,
∵在直角△ABC中,∠ABC+∠ACB=90°,
又∵∠ABC=∠ADE,
∴∠ACB+∠ADE=90°.
∵∠FCD=∠ACB,
∴∠FCD+∠ADE=90°,
∴∠CFD=90°,
∴BF⊥DE,
∵EF=FD,
∴BF垂直平分DE,
∴BD=BE,
∴△BDE是等腰三角形.
【点睛】
本题考查了旋转的性质、等腰三角形的判定、线段垂直平分线的判定和性质,熟练掌握各定理是解题的关键.
20.,.
【分析】
先由平行四边形的性质求出∠DAC,再由旋转的性质求出结论.
【详解】
在平行四边形ABCD中,AD∥BC,AD=BC,∴∠DAC=∠ACB=32°,由旋转的性质得∠C'AD=90°﹣∠DAC=58°,∴AD'=AD=BC=2.
【点睛】
本题是旋转的性质,主要考查了平行四边形的性质,旋转的性质,解答本题的关键是用旋转的性质得到对应边相等,对应角线段.
21.点为旋转中心,对应边、的夹角为旋转角即;;(3)、的位置关系为:.理由见解析.
【分析】
(1)根据旋转的性质,点D为旋转中心,对应边BD、AD的夹角为旋转角;
(2)根据旋转的性质可得BD=AD,然后根据勾股定理计算即可;
(3)延长BE交AC于F,根据旋转可得△BDE和△ADC全等,根据全等三角形对应角相等可得∠DBE=∠DAC,然后求出∠DAC+∠AEF=90°,判断出BE⊥AC.
【详解】
(1)由题意可知点D为旋转中心,对应边BD、AD的夹角为旋转角即90°;
(2)根据旋转的性质可得BD=AD=4cm,CD=2cm,∴AC===2cm;
(3)BE、AC的位置关系为:BE⊥AC.理由如下:
延长BE交AC于F.
∵△BDE按顺时针方向旋转一定角度后得到△ADC,∴△BDE≌△ADC,∴∠DBE=∠DAC.
∵∠DBE+∠BED=90°,∴∠DAC+∠AEF=90°,∴∠AFE=180°﹣90°=90°,∴BE⊥AC,∴BE、AC的位置关系为:BE⊥AC.
【点睛】
本题考查了旋转的性质和勾股定理的运用,旋转变化前后,对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.要注意旋转的三要素:①定点﹣旋转中心;②旋转方向;③旋转角度.
22.见解析
【分析】
由旋转的性质可知∠D=∠B,再根据已知条件证明AC∥DE,进而证明∠ACB=∠A,所以△ABC是等腰三角形.
【详解】
证明:由旋转知∠D=∠B,
∵∠ACD=∠B,
∴∠ACD=∠D,AC∥DE,
∴∠ACB=∠E,
又∵∠A=∠E,
∴∠ACB=∠A,
∴△ABC是等腰三角形.
【点睛】
本题考查了旋转的性质以及等腰三角形的判定,对于旋转的性质用到最多的是:旋转前、后的图形全等.
23.38°.
【详解】
分析:
如下图所示,设AC与A′B′的交点为O,则由已知条件易得∠A′OC=90°,∠ACA′=38°,由此可得∠A′=52°,由旋转的性质可得∠A=52°,结合∠ACB=90°即可得到∠ABC=38°.
详解:
∵Rt△ABC绕直角顶点C顺时针方向旋转38°得Rt△A′B′C′,
∴∠ACA′=38°,∠A=∠A′,
∵AC⊥A′B′,
∴∠A′OC=90°,
∴∠A′=90°-38°=52°,
∴∠A=52°,
又∵在Rt△ABC中,∠ACB=90°,
∴∠ABC=180°-90°-52°=38°.
点睛:“由旋转的性质得到∠ACA′=38°,结合AC⊥A′B′得到∠A′=52°=∠A”是解答本题的关键.
24.见解析
【分析】
根据旋转和平移可得∠DEB=∠ACB,∠GFE=∠A,再根据∠ABC=90°可得∠A+∠ACB=90°,进而得到∠DEB+∠GFE=90°,从而得到DE、FG的位置关系是垂直.
【详解】
解:DE⊥FG.
理由:由题知:Rt△ABC≌Rt△BDE≌Rt△FEG
∴∠A=∠BDE=∠GFE
∵∠BDE+∠BED=90°
∴∠GFE+∠BED=90°,即DE⊥FG.
试卷第2页,共5页
试卷第1页,共5页
同课章节目录
