第四章 投影与视图单元测试题(含答案)
图片预览
文档简介
中小学教育资源及组卷应用平台
《第四章 投影与视图》单元测试题
(时间:60分钟 满分:100分)
一、选择题(每小题3分,共24分)
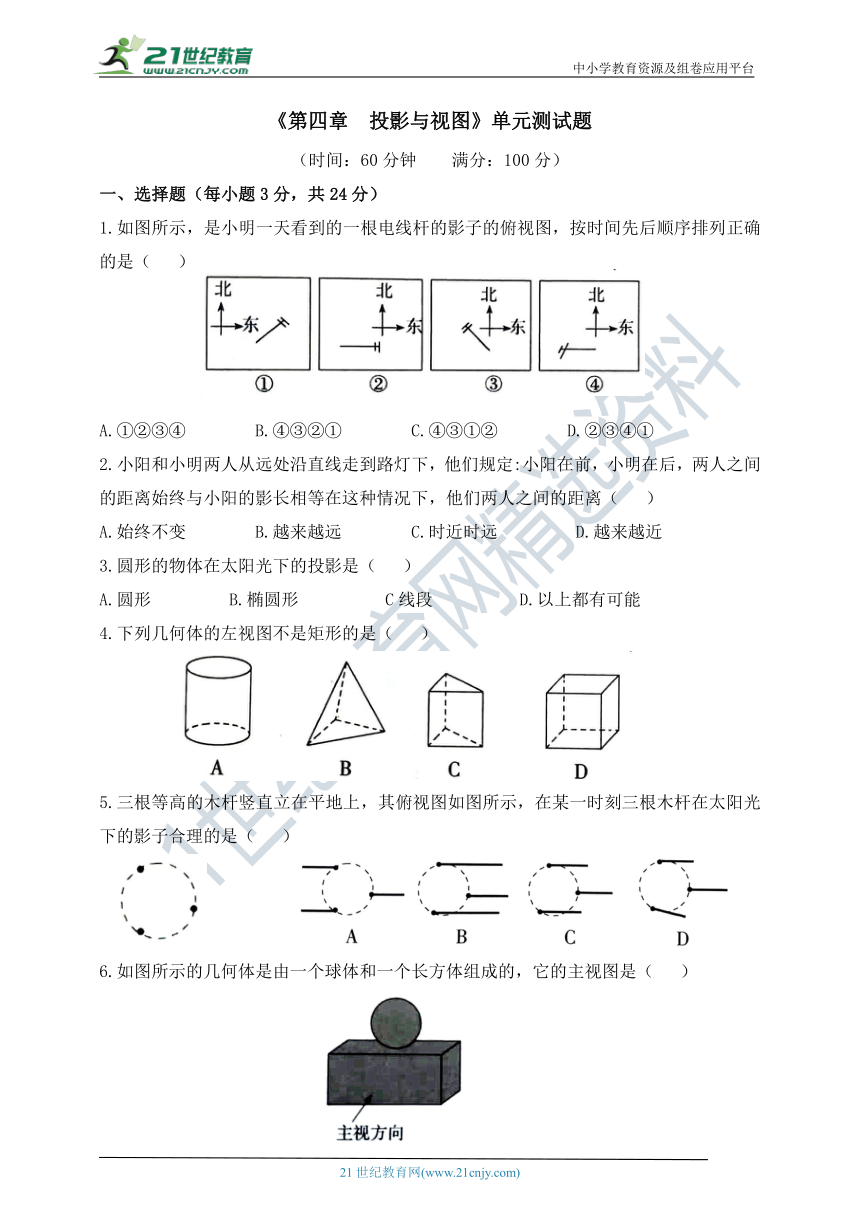
1.如图所示,是小明一天看到的一根电线杆的影子的俯视图,按时间先后顺序排列正确的是( )
A.①②③④ B.④③②① C.④③①② D.②③④①
2.小阳和小明两人从远处沿直线走到路灯下,他们规定:小阳在前,小明在后,两人之间的距离始终与小阳的影长相等在这种情况下,他们两人之间的距离( )
A.始终不变 B.越来越远 C.时近时远 D.越来越近
3.圆形的物体在太阳光下的投影是( )
A.圆形 B.椭圆形 C线段 D.以上都有可能
4.下列几何体的左视图不是矩形的是( )
5.三根等高的木杆竖直立在平地上,其俯视图如图所示,在某一时刻三根木杆在太阳光下的影子合理的是( )
6.如图所示的几何体是由一个球体和一个长方体组成的,它的主视图是( )
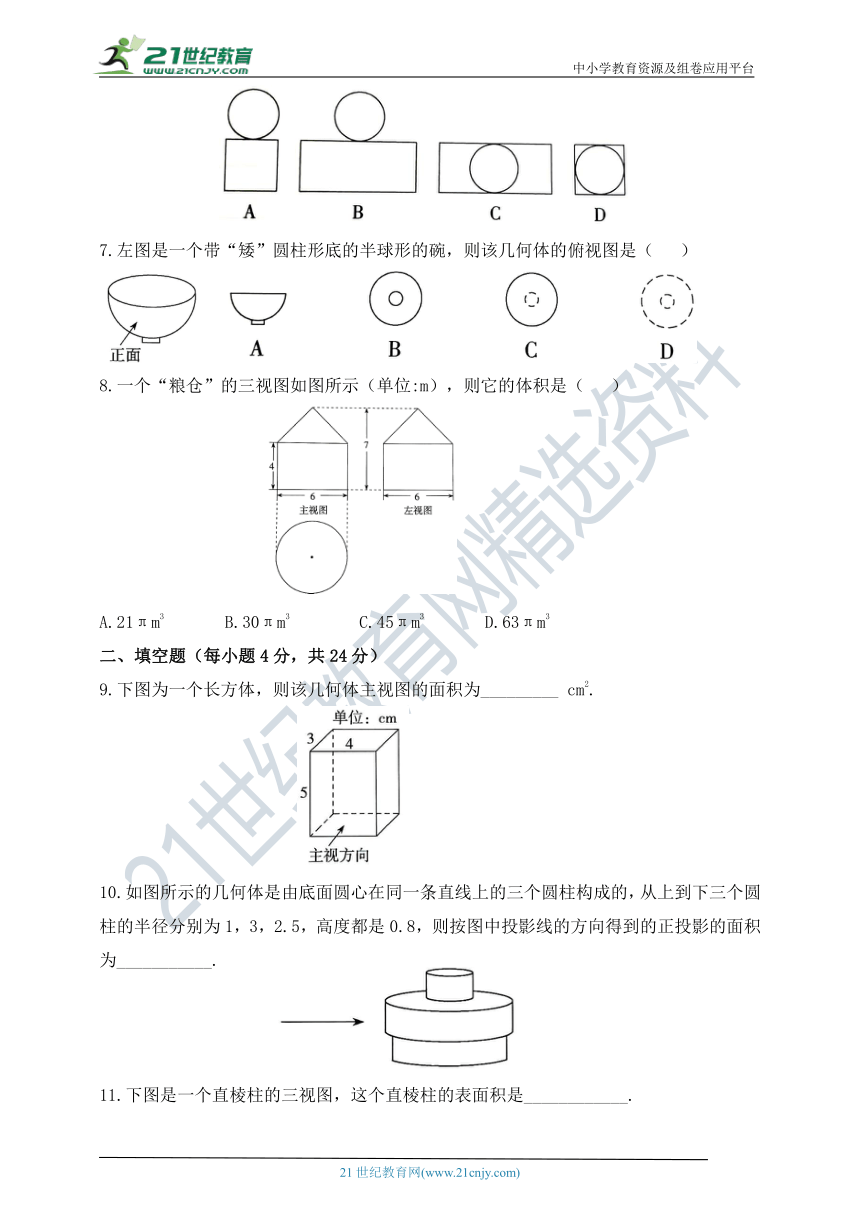
7.左图是一个带“矮”圆柱形底的半球形的碗,则该几何体的俯视图是( )
8.一个“粮仓”的三视图如图所示(单位:m),则它的体积是( )
A.21πm3 B.30πm3 C.45πm3 D.63πm3
二、填空题(每小题4分,共24分)
9.下图为一个长方体,则该几何体主视图的面积为_________ cm2.
10.如图所示的几何体是由底面圆心在同一条直线上的三个圆柱构成的,从上到下三个圆柱的半径分别为1,3,2.5,高度都是0.8,则按图中投影线的方向得到的正投影的面积为___________.
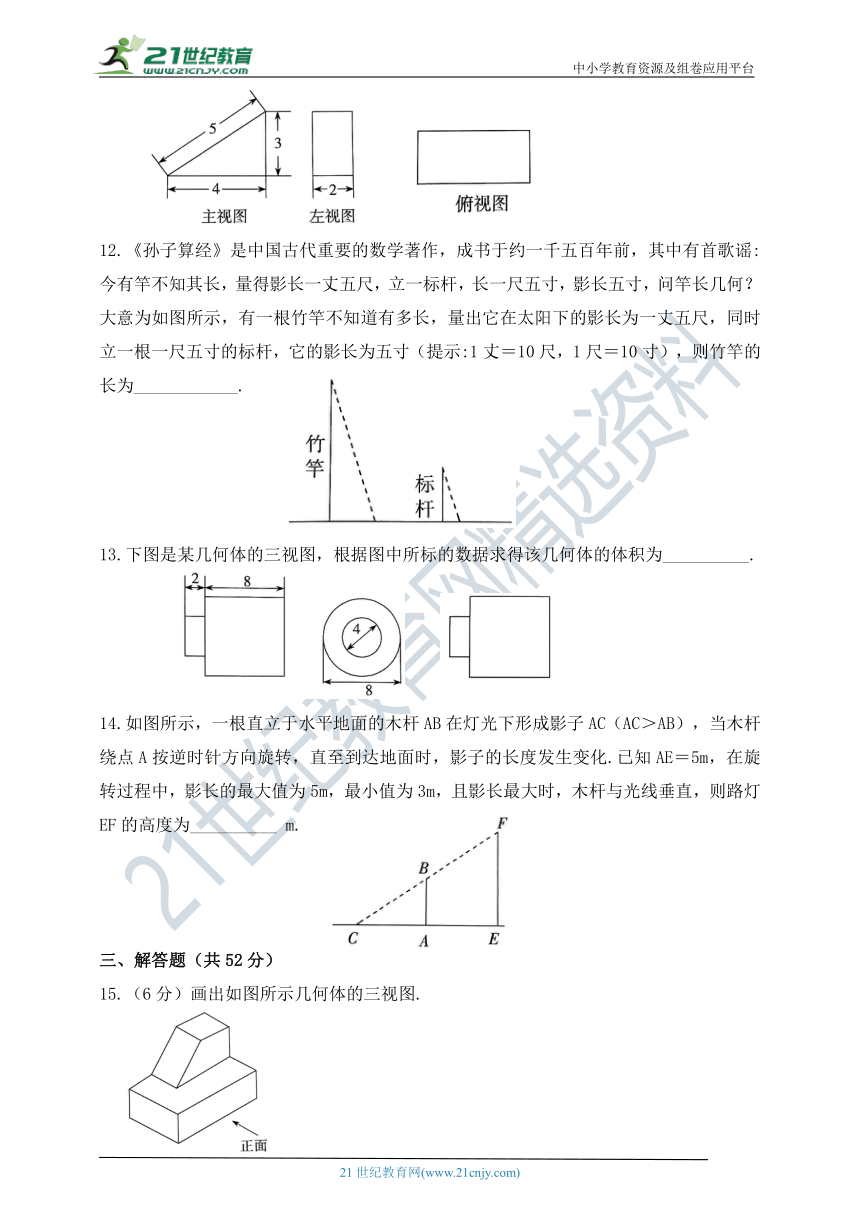
11.下图是一个直棱柱的三视图,这个直棱柱的表面积是____________.
12.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?大意为如图所示,有一根竹竿不知道有多长,量出它在太阳下的影长为一丈五尺,同时立一根一尺五寸的标杆,它的影长为五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为____________.
13.下图是某几何体的三视图,根据图中所标的数据求得该几何体的体积为__________.
14.如图所示,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5m,在旋转过程中,影长的最大值为5m,最小值为3m,且影长最大时,木杆与光线垂直,则路灯EF的高度为__________ m.
三、解答题(共52分)
15.(6分)画出如图所示几何体的三视图.
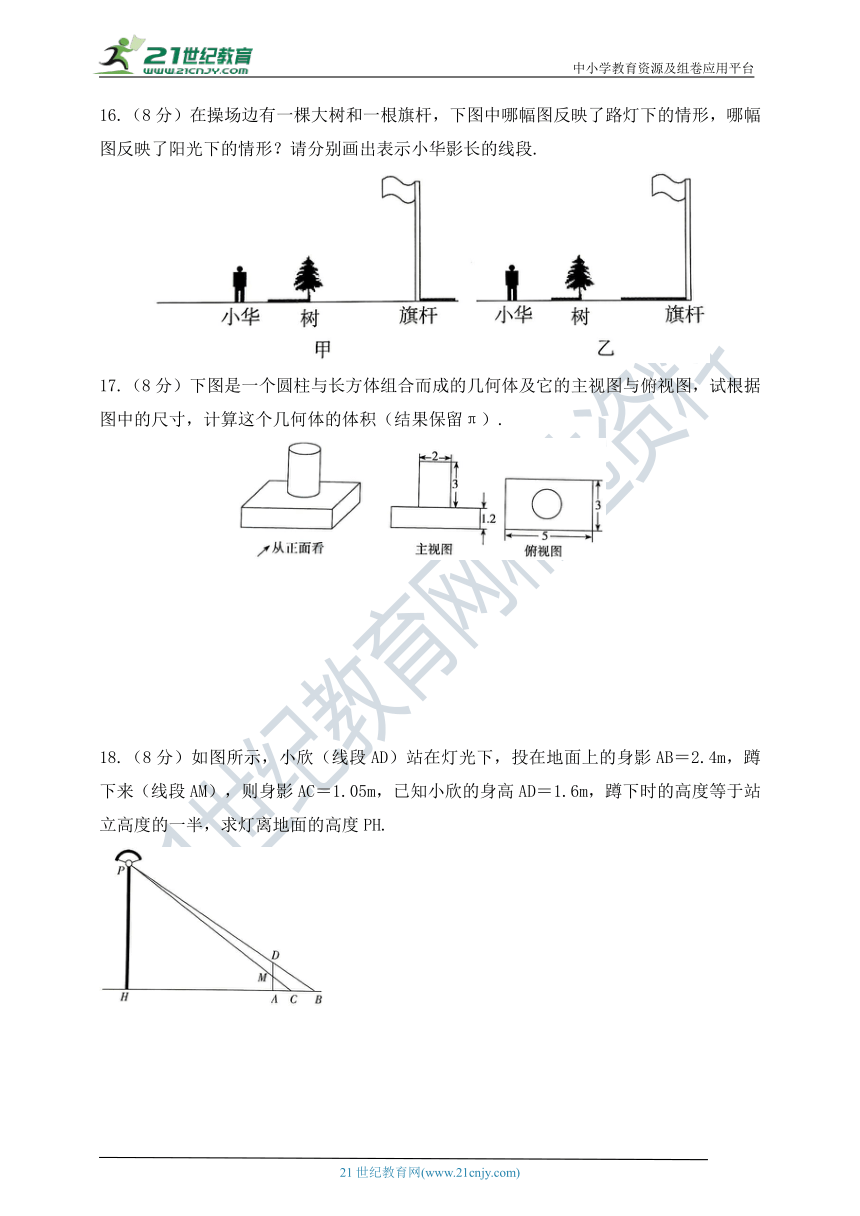
16.(8分)在操场边有一棵大树和一根旗杆,下图中哪幅图反映了路灯下的情形,哪幅图反映了阳光下的情形?请分别画出表示小华影长的线段.
17.(8分)下图是一个圆柱与长方体组合而成的几何体及它的主视图与俯视图,试根据图中的尺寸,计算这个几何体的体积(结果保留π).
18.(8分)如图所示,小欣(线段AD)站在灯光下,投在地面上的身影AB=2.4m,蹲下来(线段AM),则身影AC=1.05m,已知小欣的身高AD=1.6m,蹲下时的高度等于站立高度的一半,求灯离地面的高度PH.
19.(10分)如图所示,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗户距地面的高度OD=0.8m,窗高CD=1.2m,并测得OE=0.8m,OF=3m,求围墙AB的高度.
20.(12分)如图所示,某光源下有三根杆子,甲杆GH的影子为GM,乙杆EF的影子一部分落在地面上的EA处,一部分落在斜坡AB上的AD处.
(1)请在图4-3-17中画出形成影子的光线,确定光源所在的位置R,并画出丙杆PQ在地面上的影子;
(2)在(1)的结论下,若过点F的光线FD⊥AB,斜坡与地面的夹角为60°,AD=1米,AE=2米,请求出乙杆EF的高度.(结果保留根号)
参考答案
一、选择题
1.C 2.D 3.D 4.B 5.C 6.B 7.C 8.C
二、填空题
9. 20 10. 10.4 11. 36 12. 四丈五尺 13. 136π 14. 7.5
三、解答题
15.解析 几何体的三视图如图所示:
16.解析 如图,分别过树和旗杆的顶端与其影子的顶端画光线由图可知,图甲中的光线相交于一点O,图乙中的光线互相平行,所以图甲是路灯下的情形,图乙是阳光下的情形在图甲中过点O与小华的头顶画光线,交小华与树所在的直线于点A,线段AB即为表示小华影长的线段在图乙中过小华的头顶画光线的平行线,交小华与树所在的直线于点A′,线段A′B′即为表示小华影长的线段.
17.解析 由主视图及俯视图可得到数据:圆柱的底面直径为2,高为3;长方体的长、宽、高分别为5,3,1.2.
∴这个几何体的体积是5×3×1.2+π·×3=18+3π.
18.解析 由题意知AD∥PH,∴△ADB∽△HPB,△AMC∽△HPC.
∴,,∴,.解得HA=8.4,PH=7.2.
∴灯离地面的高度为7.2 m.
19.解析 如图,连接CD,由题意知O、D、C在一条直线上.
∵DO⊥BF,∠DOE=90°,∴OD=0.8m,OE=0.8m,∴∠DEB=45°.
∵AB⊥BF,∴∠BAE=45°,∴AB=BE.
设AB=EB=x m,∵AB⊥BF,CO⊥BF,∴AB∥CO.
∴△ABF∽△COF.∴,即.解得x=4.4.
经检验x=4.4是原分式方程的解,且符合题意.
答:围墙AB的高度是4.4 m.
20.解析 (1)如图,QN即为丙杆PQ在地面上的影子.
(2)分别延长FD、EA,交于点S.
在Rt△ADS中,∠ADS=90°,∠DAS=60°,∴∠S=30°.
又∵AD=1,∴AS=2,∴ES=AS+AE=2+2=4.
在Rt△EFS中,∠FES=90°,∠S=30°,
∴EF=ES·tanS=4tan30°=(米).
答:乙杆EF的高度为米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
《第四章 投影与视图》单元测试题
(时间:60分钟 满分:100分)
一、选择题(每小题3分,共24分)
1.如图所示,是小明一天看到的一根电线杆的影子的俯视图,按时间先后顺序排列正确的是( )
A.①②③④ B.④③②① C.④③①② D.②③④①
2.小阳和小明两人从远处沿直线走到路灯下,他们规定:小阳在前,小明在后,两人之间的距离始终与小阳的影长相等在这种情况下,他们两人之间的距离( )
A.始终不变 B.越来越远 C.时近时远 D.越来越近
3.圆形的物体在太阳光下的投影是( )
A.圆形 B.椭圆形 C线段 D.以上都有可能
4.下列几何体的左视图不是矩形的是( )
5.三根等高的木杆竖直立在平地上,其俯视图如图所示,在某一时刻三根木杆在太阳光下的影子合理的是( )
6.如图所示的几何体是由一个球体和一个长方体组成的,它的主视图是( )
7.左图是一个带“矮”圆柱形底的半球形的碗,则该几何体的俯视图是( )
8.一个“粮仓”的三视图如图所示(单位:m),则它的体积是( )
A.21πm3 B.30πm3 C.45πm3 D.63πm3
二、填空题(每小题4分,共24分)
9.下图为一个长方体,则该几何体主视图的面积为_________ cm2.
10.如图所示的几何体是由底面圆心在同一条直线上的三个圆柱构成的,从上到下三个圆柱的半径分别为1,3,2.5,高度都是0.8,则按图中投影线的方向得到的正投影的面积为___________.
11.下图是一个直棱柱的三视图,这个直棱柱的表面积是____________.
12.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?大意为如图所示,有一根竹竿不知道有多长,量出它在太阳下的影长为一丈五尺,同时立一根一尺五寸的标杆,它的影长为五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为____________.
13.下图是某几何体的三视图,根据图中所标的数据求得该几何体的体积为__________.
14.如图所示,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5m,在旋转过程中,影长的最大值为5m,最小值为3m,且影长最大时,木杆与光线垂直,则路灯EF的高度为__________ m.
三、解答题(共52分)
15.(6分)画出如图所示几何体的三视图.
16.(8分)在操场边有一棵大树和一根旗杆,下图中哪幅图反映了路灯下的情形,哪幅图反映了阳光下的情形?请分别画出表示小华影长的线段.
17.(8分)下图是一个圆柱与长方体组合而成的几何体及它的主视图与俯视图,试根据图中的尺寸,计算这个几何体的体积(结果保留π).
18.(8分)如图所示,小欣(线段AD)站在灯光下,投在地面上的身影AB=2.4m,蹲下来(线段AM),则身影AC=1.05m,已知小欣的身高AD=1.6m,蹲下时的高度等于站立高度的一半,求灯离地面的高度PH.
19.(10分)如图所示,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗户距地面的高度OD=0.8m,窗高CD=1.2m,并测得OE=0.8m,OF=3m,求围墙AB的高度.
20.(12分)如图所示,某光源下有三根杆子,甲杆GH的影子为GM,乙杆EF的影子一部分落在地面上的EA处,一部分落在斜坡AB上的AD处.
(1)请在图4-3-17中画出形成影子的光线,确定光源所在的位置R,并画出丙杆PQ在地面上的影子;
(2)在(1)的结论下,若过点F的光线FD⊥AB,斜坡与地面的夹角为60°,AD=1米,AE=2米,请求出乙杆EF的高度.(结果保留根号)
参考答案
一、选择题
1.C 2.D 3.D 4.B 5.C 6.B 7.C 8.C
二、填空题
9. 20 10. 10.4 11. 36 12. 四丈五尺 13. 136π 14. 7.5
三、解答题
15.解析 几何体的三视图如图所示:
16.解析 如图,分别过树和旗杆的顶端与其影子的顶端画光线由图可知,图甲中的光线相交于一点O,图乙中的光线互相平行,所以图甲是路灯下的情形,图乙是阳光下的情形在图甲中过点O与小华的头顶画光线,交小华与树所在的直线于点A,线段AB即为表示小华影长的线段在图乙中过小华的头顶画光线的平行线,交小华与树所在的直线于点A′,线段A′B′即为表示小华影长的线段.
17.解析 由主视图及俯视图可得到数据:圆柱的底面直径为2,高为3;长方体的长、宽、高分别为5,3,1.2.
∴这个几何体的体积是5×3×1.2+π·×3=18+3π.
18.解析 由题意知AD∥PH,∴△ADB∽△HPB,△AMC∽△HPC.
∴,,∴,.解得HA=8.4,PH=7.2.
∴灯离地面的高度为7.2 m.
19.解析 如图,连接CD,由题意知O、D、C在一条直线上.
∵DO⊥BF,∠DOE=90°,∴OD=0.8m,OE=0.8m,∴∠DEB=45°.
∵AB⊥BF,∴∠BAE=45°,∴AB=BE.
设AB=EB=x m,∵AB⊥BF,CO⊥BF,∴AB∥CO.
∴△ABF∽△COF.∴,即.解得x=4.4.
经检验x=4.4是原分式方程的解,且符合题意.
答:围墙AB的高度是4.4 m.
20.解析 (1)如图,QN即为丙杆PQ在地面上的影子.
(2)分别延长FD、EA,交于点S.
在Rt△ADS中,∠ADS=90°,∠DAS=60°,∴∠S=30°.
又∵AD=1,∴AS=2,∴ES=AS+AE=2+2=4.
在Rt△EFS中,∠FES=90°,∠S=30°,
∴EF=ES·tanS=4tan30°=(米).
答:乙杆EF的高度为米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
