4.4.3 不同函数增长的差异教学课件- 2021-2022学年高一上学期数学人教A版(2019)必修第一册(共21张PPT)
文档属性
| 名称 | 4.4.3 不同函数增长的差异教学课件- 2021-2022学年高一上学期数学人教A版(2019)必修第一册(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
4.4 对数函数
4.4.3 不同函数增长的差异
复习引入
思考:在前面,我们学习过的一次函数、指数函数、对数函数,这些函数在情况下的是增函数?
虽然它们都是增函数,但增长方式存在很大差异,这种差异正是不同类型现实问题具有不同增长规律的反映. 如果我们知道不同函数增长方式的差异,就可以根据现实问题中的增长情况,选择合适的函数模型来刻画其变化规律。
下面就来研究一次函数 ,指数函数 ,对数函数内增长方式的差异.
知识探究
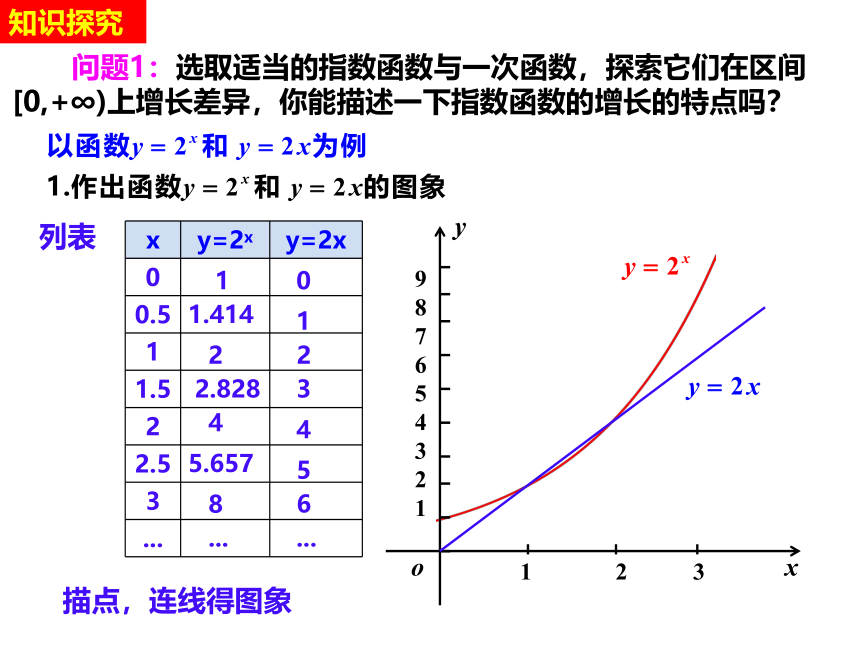
问题1:选取适当的指数函数与一次函数,探索它们在区间[0,+∞)上增长差异,你能描述一下指数函数的增长的特点吗?
列表
x y=2x y=2x
0
0.5
1
1.5
2
2.5
3
...
1
1.414
2
2.828
4
5.657
8
0
1
2
3
4
5
6
...
...
描点,连线得图象
1 2 3
9
8
7
6
5
4
3
2
1
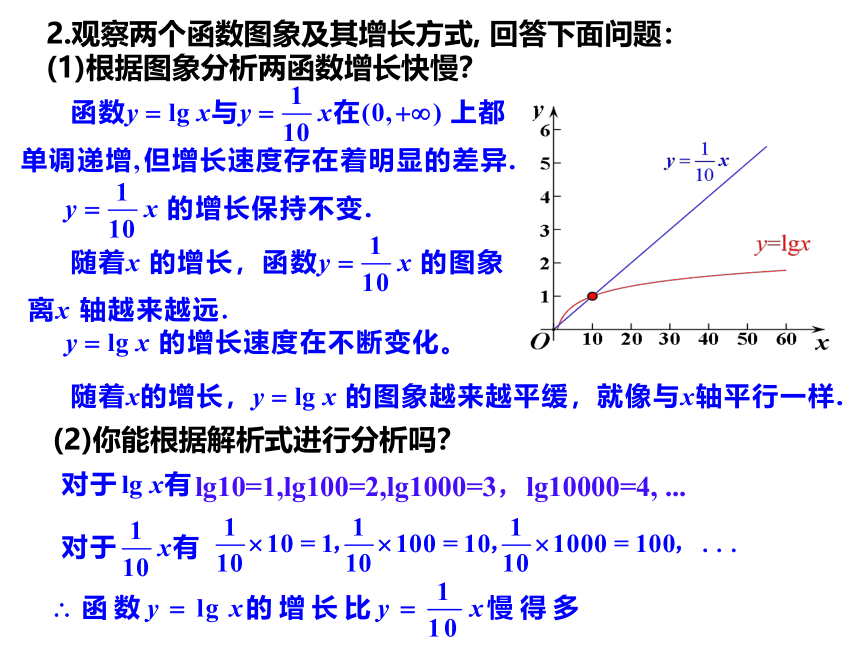
2.观察两个函数图象及其增长方式, 回答下面问题:
(1)两函数图象的交点是什么?
(2)两图像的关系是什么?
(3)总结两图像增长变化情况?
函数y=2x与y=2x有两个交点:(1,2),(2,4);
在区间[0,1)上,y=2x的图象位于y=2x上方;
在区间(1,2)上,y=2x的图象位于y=2x下方;
在区间(1,2)上,y=2x的图象位于y=2x下方。
y=2x与y=2x都是增函数,但是它们的增长速度不同。
函数y=2x的增长速度不变,y=2x的增长速度是变化的。
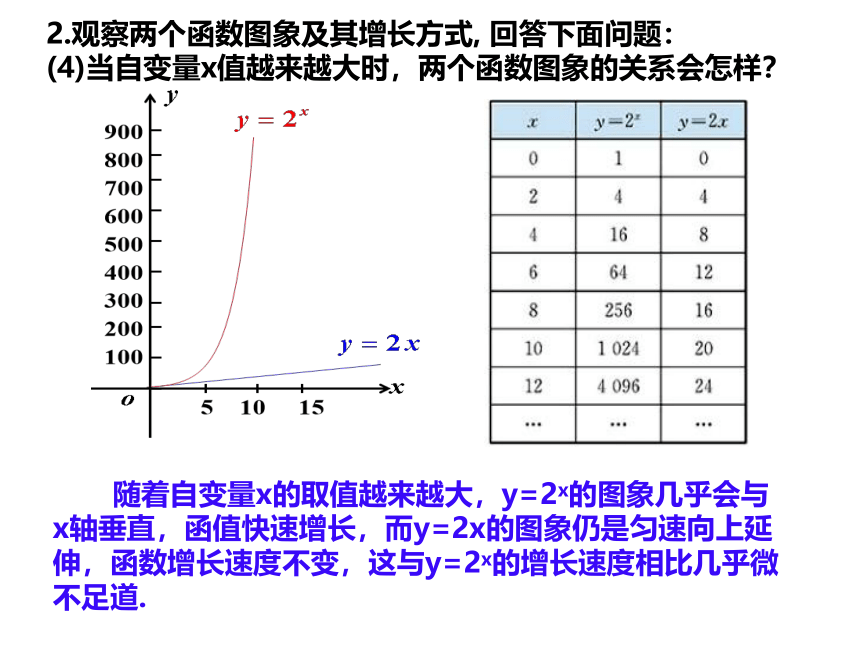
(4)当自变量x值越来越大时,两个函数图象的关系会怎样?
2.观察两个函数图象及其增长方式, 回答下面问题:
(4)当自变量x值越来越大时,两个函数图象的关系会怎样?
随着自变量x的取值越来越大,y=2x的图象几乎会与x轴垂直,函值快速增长,而y=2x的图象仍是匀速向上延伸,函数增长速度不变,这与y=2x的增长速度相比几乎微不足道.
2.观察两个函数图象及其增长方式, 回答下面问题:
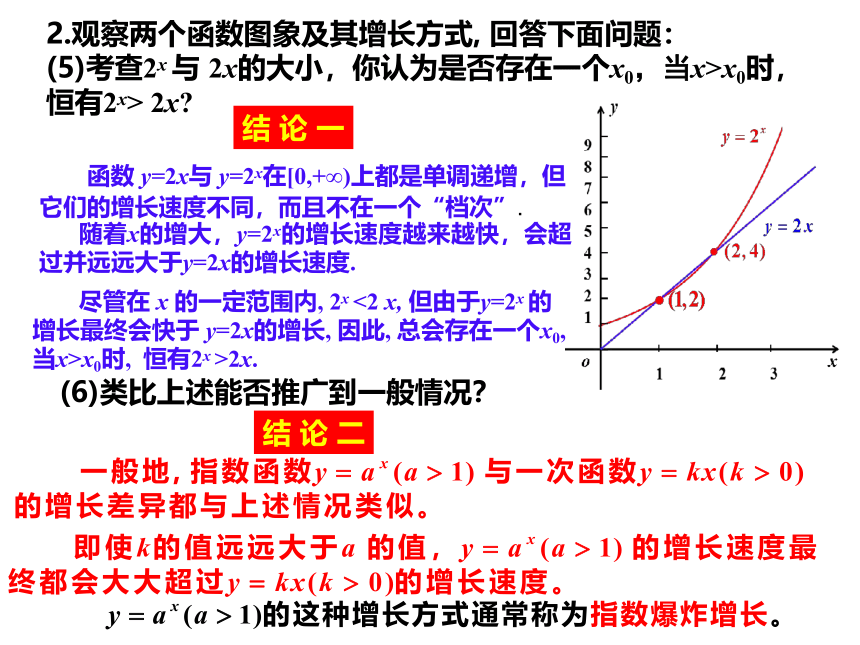
(5)考查2x 与 2x的大小,你认为是否存在一个x0,当x>x0时,恒有2x> 2x
(6)类比上述能否推广到一般情况?
尽管在 x 的一定范围内, 2x <2 x, 但由于y=2x 的增长最终会快于 y=2x的增长, 因此, 总会存在一个x0, 当x>x0时, 恒有2x >2x.
函数 y=2x与 y=2x在[0,+∞)上都是单调递增,但它们的增长速度不同,而且不在一个“档次”.
随着x的增大,y=2x的增长速度越来越快,会超过并远远大于y=2x的增长速度.
结论一
结论二
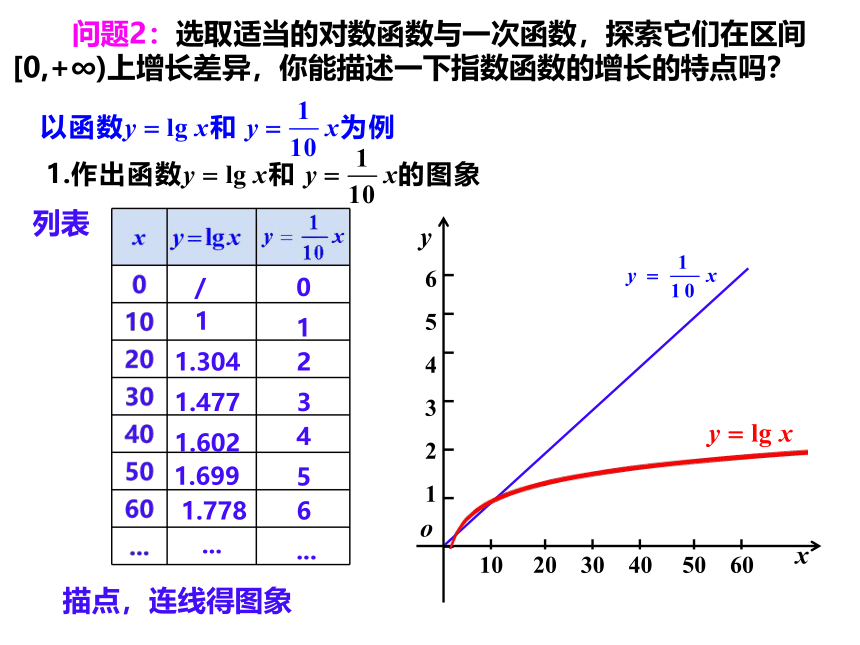
问题2:选取适当的对数函数与一次函数,探索它们在区间[0,+∞)上增长差异,你能描述一下指数函数的增长的特点吗?
列表
/
1.304
1.477
1.602
1.699
1.778
1
0
1
2
3
4
5
6
...
...
描点,连线得图象
6
5
4
3
2
1
10 20 30 40 50 60
2.观察两个函数图象及其增长方式, 回答下面问题:
(1)根据图象分析两函数增长快慢?
(2)你能根据解析式进行分析吗?
lg10=1,lg100=2,lg1000=3,lg10000=4, ...
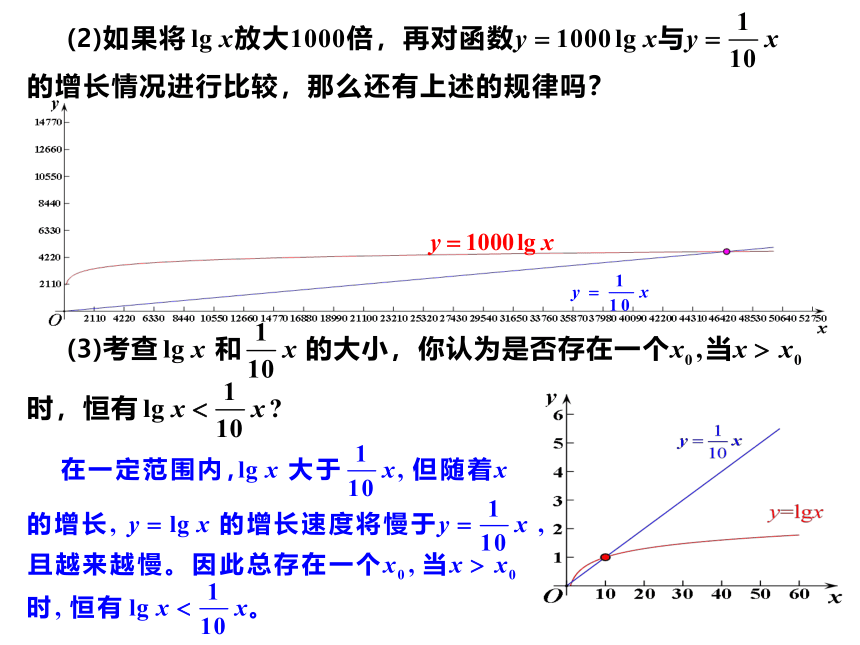
(3)类比上述能否推广到一般情况?
结论三
问题3: (1)画出一次函数y=2x ,对数函数y=lgx和指数函数y=2x的图象,并比较它们的增长差异?
函数y=2x ,y=lgx与y=2x在(0,+∞)上都是单调递增,但它们的增长速度存在明显差异.
y=2x在(0,+∞)上增长速度不变,函数y=lgx与y=2x在(0,+∞)上的增长速度在变化.
函数y=2x的增长速度越来越快,图象越来越陡,就像与 x 轴垂直一样;函数y=lgx的增长速度越来越慢,图象越来越平缓,就像与x轴平行一样.
(2)概括一次函数y=kx(k>0) ,对数函数y=logax(a>1)和指数函数y=bx(b>1) 的增长差异.
一般地,一次函数y=kx(k>0) ,对数函数y=logax(a>1)和指数函数y=bx(b>1) 在(0,+∞)上都是单调递增,但它们的增长速度不同.
随着x的增大,一次函数y=kx(k>0) 保持固定的增长速度,而指数函数y=bx(b>1)的增长速度越来越快;对数函数y=logax(a>1的增长速度越来越慢.
不论b值比k值小多少,在一定范围内,bx可能会小于kx ,但由于y=bx的增长会快于y=kx的增长,因此总存在一个x0 ,当 x>x0时,恒有bx>kx. ;
不论a值比k值大多少,在一定范围内,logax可能会大于kx ,但由于y=logax的增长会慢于y=kx的增长,因此总存在一个x0 ,当x>x0时,恒有kx>logax.
(3)讨论交流“直线上升”“对数增长”“指数爆炸”的含义.
(1)直线上升: y=kx(k>0)的增长方式
增长速度不变,是一个固定的值;
(2)对数增长:y=logax(a>1)的增长方式
增长速度越来越慢,图象越来越平缓,就像与x 轴平行一样;
(3)指数爆炸:y=ax(a>1)的增长方式
增长速度越来越快,以相同倍数增加,图象越来越陡,最终就像与 x轴垂直一样.
例1.(1)随着x的不断增加,下列函数中增长速度最快的是( )
A.y=2 021x ;B.y=x2 021; C.y=log2 021x; D.y=2 021 x
例析
A
(2)当我们在做化学实验时,常常需要将溶液注入容器中,当溶液注入容器(设单位时间内流入的溶液量相同)时,溶液的高度随着时间的变化而变化,在图中请选择与容器相匹配的图象,A对应_______;B对应_______;C对应_______;D对应_______.
(4)
(1)
(3)
(2)
例2.已知函数 f(x)=2x 和 g(x)=x3 的图象如图,设两个函数的图象相交于点A(x1, y1) 和 B(x2, y2), 且x1(1)请指出图中曲线C1,C2分别对应哪一个函数;
(2)若x1∈[a,a+1], x2∈[b,b+1], 且a, b∈{1,2,3,4,5,6,7,8,9,10,11,12},指出a, b 的值,并说明理由.
(1)由指数函数与幂函数的增长速度知
C1 对应函数 g(x)=x3,
C2 对应函数 f(x)=2x.
(2)由图象得 f(x1)=g(x1), f(x2)=g(x2)
当 xx3, 即 f(x)>g(x);
当 x1当 x>x2时, f(x)>g(x).
∵ f(1)=2, g(1)=1, f(2)=4, g(2)=8
∴由f(1)>g(1), f(2)x1∈[1,2], 即a=1.
又∵f(9)=29=512, g(9)=93=729
f(10)=1024, g(10)=1000
∴由 f(9)g(10)得
x2∈[9,10],即b=9.
综上可知, a=1, b=9.
解:
例3.某化工厂开发研制了一种新产品,在前三个月的月生产量依次为100 t, 120 t, 130 t. 为了预测今后各个月的生产量, 需要以这三个月的月产量为依据, 用一个函数来模拟月产量y与月序数x之间的关系. 根据以往的经验,可选用二次函数模型y=f(x)(x∈N*)或指数函数模型y=g(x)(x∈N*), 现在已知该厂这种新产品在第四个月的月产量为136 t,则试问选用哪一个作为模拟函数较好
设 f(x)=ax2+bx+c(a≠0),则由题意得
同理, 可设 g(x)=max+n(a>0且a≠1)
∴f(x)= -5x2+35x+70.
当x=4 时,
f(4)= -5×42+35×4+70=130
g(4)= -80×0.54+140=135
由g(1)=100, g(2)=120, g(3)=
130得
即 g(4)在数值上更为接近第四个月的实际月产量.
∴ 选用指数函数模型较好.
解:
1.三个变量y1,y2,y3,y4随变量x变化的数据如下表:
则关于x呈指数型函数变化的变量是________
练习
x 0 5 10 15 20 25 30
y1 5 130 505 1130 2005 3130 4505
y2 5 90 1620 29160 524880 9447840 170061120
y3 5 30 55 80 105 130 155
y2
2.(1)(2)(3)分别是y=3x与y=5x在不同范围内的图象,估算出使3x > 5x的x的取值范围(参考数据:30.27= 1.35,32.17= 10.85).
(教材P39练习第1,2,3,4题)
4.函数y=f(x)的图象如图所示,则y=f(x)可能是( )
3.如图,对数函数y=lgx与一次函数y=f(x)的图象有A,B两个
公共点, 求一次函数的解析式。
简析:
课堂小结
1.在探究不同函数的增长方式的过程中主要的数学思想方法有哪些?
一般与特殊的思想方法;
数形结合的思想方法
2.说说一次函数,指数函数,对数函数增长方式的差异?
y=ax(a>1) y=logbx(b>1) y=kx(k>0)
在(0,+∞)上的单调性 单调递增
增长速度 越来越快 越来越慢 固定不变
图象的变化 随x的增大逐渐变陡,几乎与x轴垂直 随x的增大逐渐变平,几乎与x轴平行 图象几乎呈
一条直线匀
速上升
形象描述 指数爆炸 对数增长 直线上升
增长结果 总存在一个x0,当x>x0时,有
ax>kx>logbx
4.对于幂函数y=xα(α>0)的增长方式,你有什么看法?
(1)幂函数y=xα(α>0)增长快慢与α的大小有关;
(2)幂函数y=xα(α>0)的增长速度介于指数函数和对数函数之间.
(1)函数值的大小不等同于增长速度快慢,数值大不一定增长速度快,增长速度体现在函数值的变化趋势上;
(2)y=ax的增长速度越来越快,y=logbx越来越慢,最后,y=ax的增长速度会远远大于y=kx的增长速度y=logbx的增长速度会远远小于y=kx的增长速度。这样一直下去,总会在某个x取某个值(x0)以后,会出现ax>kx>logbx.
3.怎样理解当a>1,b>1,k>0时“总存在一个x0,当x>x0时, ax>kx>logbx”?
作 业
教材P140习题4.4
第6,10,11题
4.4 对数函数
4.4.3 不同函数增长的差异
复习引入
思考:在前面,我们学习过的一次函数、指数函数、对数函数,这些函数在情况下的是增函数?
虽然它们都是增函数,但增长方式存在很大差异,这种差异正是不同类型现实问题具有不同增长规律的反映. 如果我们知道不同函数增长方式的差异,就可以根据现实问题中的增长情况,选择合适的函数模型来刻画其变化规律。
下面就来研究一次函数 ,指数函数 ,对数函数内增长方式的差异.
知识探究
问题1:选取适当的指数函数与一次函数,探索它们在区间[0,+∞)上增长差异,你能描述一下指数函数的增长的特点吗?
列表
x y=2x y=2x
0
0.5
1
1.5
2
2.5
3
...
1
1.414
2
2.828
4
5.657
8
0
1
2
3
4
5
6
...
...
描点,连线得图象
1 2 3
9
8
7
6
5
4
3
2
1
2.观察两个函数图象及其增长方式, 回答下面问题:
(1)两函数图象的交点是什么?
(2)两图像的关系是什么?
(3)总结两图像增长变化情况?
函数y=2x与y=2x有两个交点:(1,2),(2,4);
在区间[0,1)上,y=2x的图象位于y=2x上方;
在区间(1,2)上,y=2x的图象位于y=2x下方;
在区间(1,2)上,y=2x的图象位于y=2x下方。
y=2x与y=2x都是增函数,但是它们的增长速度不同。
函数y=2x的增长速度不变,y=2x的增长速度是变化的。
(4)当自变量x值越来越大时,两个函数图象的关系会怎样?
2.观察两个函数图象及其增长方式, 回答下面问题:
(4)当自变量x值越来越大时,两个函数图象的关系会怎样?
随着自变量x的取值越来越大,y=2x的图象几乎会与x轴垂直,函值快速增长,而y=2x的图象仍是匀速向上延伸,函数增长速度不变,这与y=2x的增长速度相比几乎微不足道.
2.观察两个函数图象及其增长方式, 回答下面问题:
(5)考查2x 与 2x的大小,你认为是否存在一个x0,当x>x0时,恒有2x> 2x
(6)类比上述能否推广到一般情况?
尽管在 x 的一定范围内, 2x <2 x, 但由于y=2x 的增长最终会快于 y=2x的增长, 因此, 总会存在一个x0, 当x>x0时, 恒有2x >2x.
函数 y=2x与 y=2x在[0,+∞)上都是单调递增,但它们的增长速度不同,而且不在一个“档次”.
随着x的增大,y=2x的增长速度越来越快,会超过并远远大于y=2x的增长速度.
结论一
结论二
问题2:选取适当的对数函数与一次函数,探索它们在区间[0,+∞)上增长差异,你能描述一下指数函数的增长的特点吗?
列表
/
1.304
1.477
1.602
1.699
1.778
1
0
1
2
3
4
5
6
...
...
描点,连线得图象
6
5
4
3
2
1
10 20 30 40 50 60
2.观察两个函数图象及其增长方式, 回答下面问题:
(1)根据图象分析两函数增长快慢?
(2)你能根据解析式进行分析吗?
lg10=1,lg100=2,lg1000=3,lg10000=4, ...
(3)类比上述能否推广到一般情况?
结论三
问题3: (1)画出一次函数y=2x ,对数函数y=lgx和指数函数y=2x的图象,并比较它们的增长差异?
函数y=2x ,y=lgx与y=2x在(0,+∞)上都是单调递增,但它们的增长速度存在明显差异.
y=2x在(0,+∞)上增长速度不变,函数y=lgx与y=2x在(0,+∞)上的增长速度在变化.
函数y=2x的增长速度越来越快,图象越来越陡,就像与 x 轴垂直一样;函数y=lgx的增长速度越来越慢,图象越来越平缓,就像与x轴平行一样.
(2)概括一次函数y=kx(k>0) ,对数函数y=logax(a>1)和指数函数y=bx(b>1) 的增长差异.
一般地,一次函数y=kx(k>0) ,对数函数y=logax(a>1)和指数函数y=bx(b>1) 在(0,+∞)上都是单调递增,但它们的增长速度不同.
随着x的增大,一次函数y=kx(k>0) 保持固定的增长速度,而指数函数y=bx(b>1)的增长速度越来越快;对数函数y=logax(a>1的增长速度越来越慢.
不论b值比k值小多少,在一定范围内,bx可能会小于kx ,但由于y=bx的增长会快于y=kx的增长,因此总存在一个x0 ,当 x>x0时,恒有bx>kx. ;
不论a值比k值大多少,在一定范围内,logax可能会大于kx ,但由于y=logax的增长会慢于y=kx的增长,因此总存在一个x0 ,当x>x0时,恒有kx>logax.
(3)讨论交流“直线上升”“对数增长”“指数爆炸”的含义.
(1)直线上升: y=kx(k>0)的增长方式
增长速度不变,是一个固定的值;
(2)对数增长:y=logax(a>1)的增长方式
增长速度越来越慢,图象越来越平缓,就像与x 轴平行一样;
(3)指数爆炸:y=ax(a>1)的增长方式
增长速度越来越快,以相同倍数增加,图象越来越陡,最终就像与 x轴垂直一样.
例1.(1)随着x的不断增加,下列函数中增长速度最快的是( )
A.y=2 021x ;B.y=x2 021; C.y=log2 021x; D.y=2 021 x
例析
A
(2)当我们在做化学实验时,常常需要将溶液注入容器中,当溶液注入容器(设单位时间内流入的溶液量相同)时,溶液的高度随着时间的变化而变化,在图中请选择与容器相匹配的图象,A对应_______;B对应_______;C对应_______;D对应_______.
(4)
(1)
(3)
(2)
例2.已知函数 f(x)=2x 和 g(x)=x3 的图象如图,设两个函数的图象相交于点A(x1, y1) 和 B(x2, y2), 且x1
(2)若x1∈[a,a+1], x2∈[b,b+1], 且a, b∈{1,2,3,4,5,6,7,8,9,10,11,12},指出a, b 的值,并说明理由.
(1)由指数函数与幂函数的增长速度知
C1 对应函数 g(x)=x3,
C2 对应函数 f(x)=2x.
(2)由图象得 f(x1)=g(x1), f(x2)=g(x2)
当 x
当 x1
∵ f(1)=2, g(1)=1, f(2)=4, g(2)=8
∴由f(1)>g(1), f(2)
又∵f(9)=29=512, g(9)=93=729
f(10)=1024, g(10)=1000
∴由 f(9)
x2∈[9,10],即b=9.
综上可知, a=1, b=9.
解:
例3.某化工厂开发研制了一种新产品,在前三个月的月生产量依次为100 t, 120 t, 130 t. 为了预测今后各个月的生产量, 需要以这三个月的月产量为依据, 用一个函数来模拟月产量y与月序数x之间的关系. 根据以往的经验,可选用二次函数模型y=f(x)(x∈N*)或指数函数模型y=g(x)(x∈N*), 现在已知该厂这种新产品在第四个月的月产量为136 t,则试问选用哪一个作为模拟函数较好
设 f(x)=ax2+bx+c(a≠0),则由题意得
同理, 可设 g(x)=max+n(a>0且a≠1)
∴f(x)= -5x2+35x+70.
当x=4 时,
f(4)= -5×42+35×4+70=130
g(4)= -80×0.54+140=135
由g(1)=100, g(2)=120, g(3)=
130得
即 g(4)在数值上更为接近第四个月的实际月产量.
∴ 选用指数函数模型较好.
解:
1.三个变量y1,y2,y3,y4随变量x变化的数据如下表:
则关于x呈指数型函数变化的变量是________
练习
x 0 5 10 15 20 25 30
y1 5 130 505 1130 2005 3130 4505
y2 5 90 1620 29160 524880 9447840 170061120
y3 5 30 55 80 105 130 155
y2
2.(1)(2)(3)分别是y=3x与y=5x在不同范围内的图象,估算出使3x > 5x的x的取值范围(参考数据:30.27= 1.35,32.17= 10.85).
(教材P39练习第1,2,3,4题)
4.函数y=f(x)的图象如图所示,则y=f(x)可能是( )
3.如图,对数函数y=lgx与一次函数y=f(x)的图象有A,B两个
公共点, 求一次函数的解析式。
简析:
课堂小结
1.在探究不同函数的增长方式的过程中主要的数学思想方法有哪些?
一般与特殊的思想方法;
数形结合的思想方法
2.说说一次函数,指数函数,对数函数增长方式的差异?
y=ax(a>1) y=logbx(b>1) y=kx(k>0)
在(0,+∞)上的单调性 单调递增
增长速度 越来越快 越来越慢 固定不变
图象的变化 随x的增大逐渐变陡,几乎与x轴垂直 随x的增大逐渐变平,几乎与x轴平行 图象几乎呈
一条直线匀
速上升
形象描述 指数爆炸 对数增长 直线上升
增长结果 总存在一个x0,当x>x0时,有
ax>kx>logbx
4.对于幂函数y=xα(α>0)的增长方式,你有什么看法?
(1)幂函数y=xα(α>0)增长快慢与α的大小有关;
(2)幂函数y=xα(α>0)的增长速度介于指数函数和对数函数之间.
(1)函数值的大小不等同于增长速度快慢,数值大不一定增长速度快,增长速度体现在函数值的变化趋势上;
(2)y=ax的增长速度越来越快,y=logbx越来越慢,最后,y=ax的增长速度会远远大于y=kx的增长速度y=logbx的增长速度会远远小于y=kx的增长速度。这样一直下去,总会在某个x取某个值(x0)以后,会出现ax>kx>logbx.
3.怎样理解当a>1,b>1,k>0时“总存在一个x0,当x>x0时, ax>kx>logbx”?
作 业
教材P140习题4.4
第6,10,11题
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
