人教版2021-2022学年八年级数学上册12.2.5 用“HL”判定三角形全等 同步测试卷(word版、含答案)
文档属性
| 名称 | 人教版2021-2022学年八年级数学上册12.2.5 用“HL”判定三角形全等 同步测试卷(word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 161.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 00:00:00 | ||
图片预览

文档简介
12.2.5 用“HL”判定三角形全等同步测试卷 2021-2022学年人教版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共6小题,共18分)
下列条件中,不能判定两个直角三角形全等的是()
A. 一个锐角和斜边对应相等 B. 两条直角边对应相等
C. 两个锐角对应相等 D. 斜边和一条直角边对应相等
如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是()
A. B.
C. D.
如图,CEAB,DFAB,垂足分别为E、F,AF=BE,且AC=BD,则下列结论不一定正确的是( )
A. B.
C. D.
如图,AB⊥AC于点A,BD⊥CD于点D,若AC=DB,则下列结论中不正确的是()
A. B.
C. D.
如图,△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD和CE相交于O,AO的延长线交BC于F,则图中全等的直角三角形有()
A. 对 B. 对
C. 对 D. 对
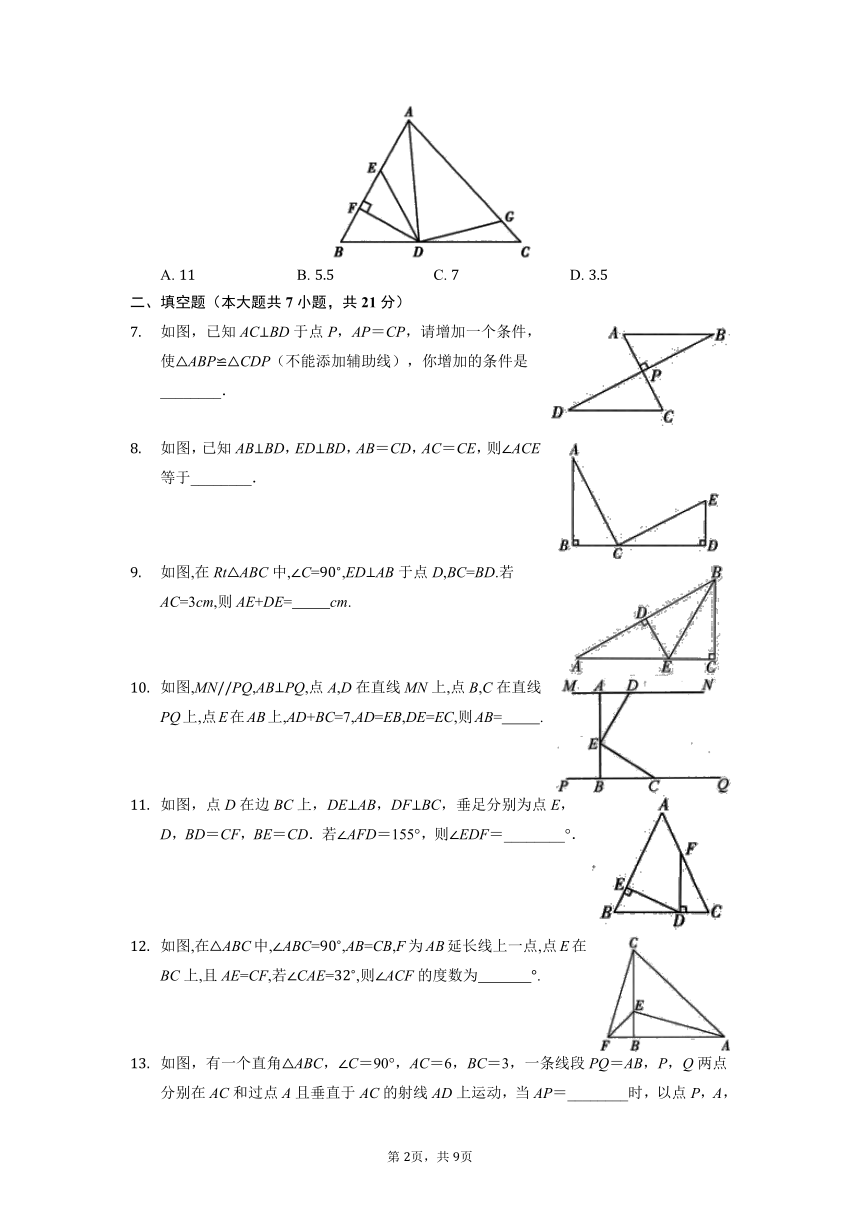
如图,AD是ABC的角平分线,DFAB,垂足为F,DE=DG,ADG和AED的面积分别为50和39,则EDF的面积为( )
A. B. C. D.
二、填空题(本大题共7小题,共21分)
如图,已知AC⊥BD于点P,AP=CP,请增加一个条件,使△ABP≌△CDP(不能添加辅助线),你增加的条件是________.
如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE等于________.
如图,在RtABC中,C=,EDAB于点D,BC=BD.若AC=3cm,则AE+DE= cm.
如图,MNPQ,ABPQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB= .
如图,点D在边BC上,DE⊥AB,DF⊥BC,垂足分别为点E,D,BD=CF,BE=CD.若∠AFD=155°,则∠EDF=________°.
如图,在ABC中,ABC=,AB=CB,F为AB延长线上一点,点E在BC上,且AE=CF,若CAE=,则ACF的度数为 .
如图,有一个直角△ABC,∠C=90°,AC=6,BC=3,一条线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AD上运动,当AP=________时,以点P,A,Q为顶点的三角形与△ABC全等.
三、解答题(本大题共5小题,共61分)
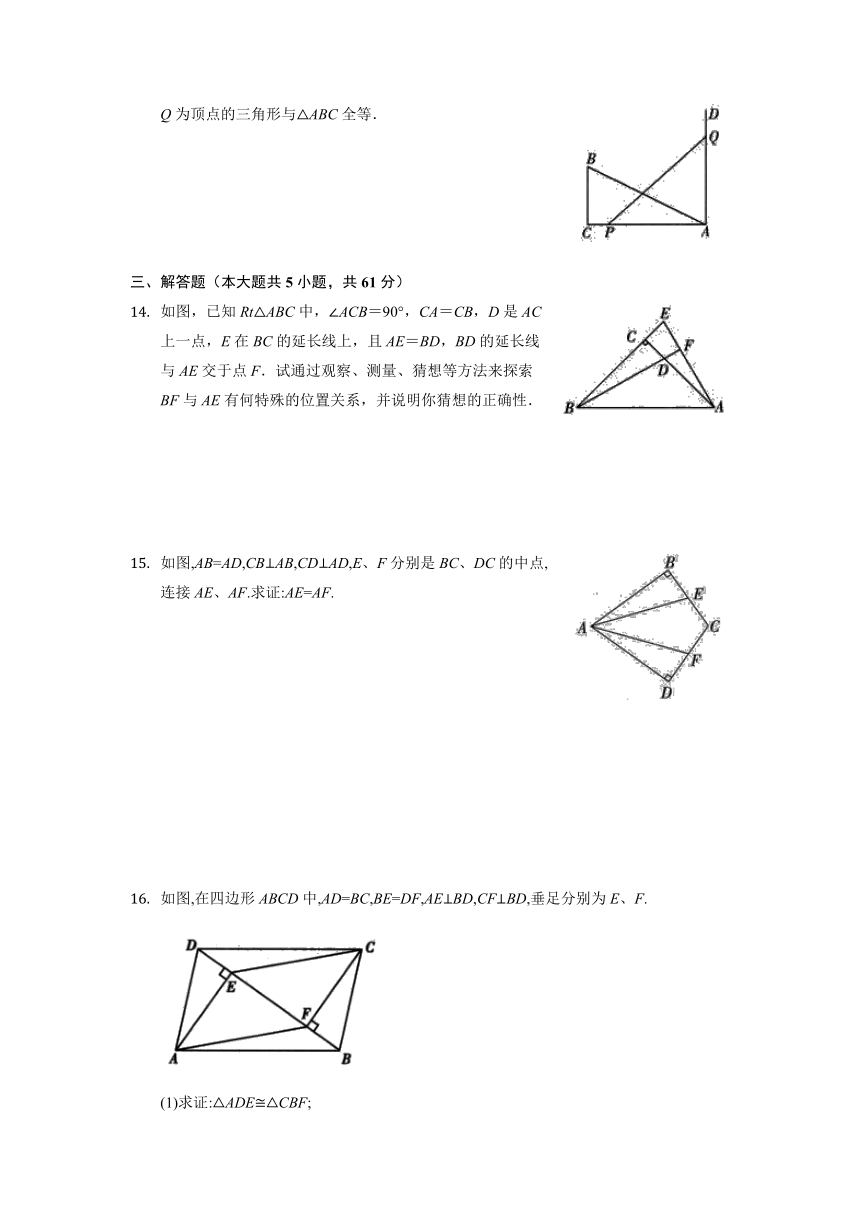
如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.
如图,AB=AD,CBAB,CDAD,E、F分别是BC、DC的中点,连接AE、AF.求证:AE=AF.
如图,在四边形ABCD中,AD=BC,BE=DF,AEBD,CFBD,垂足分别为E、F.
(1)求证:ADECBF;
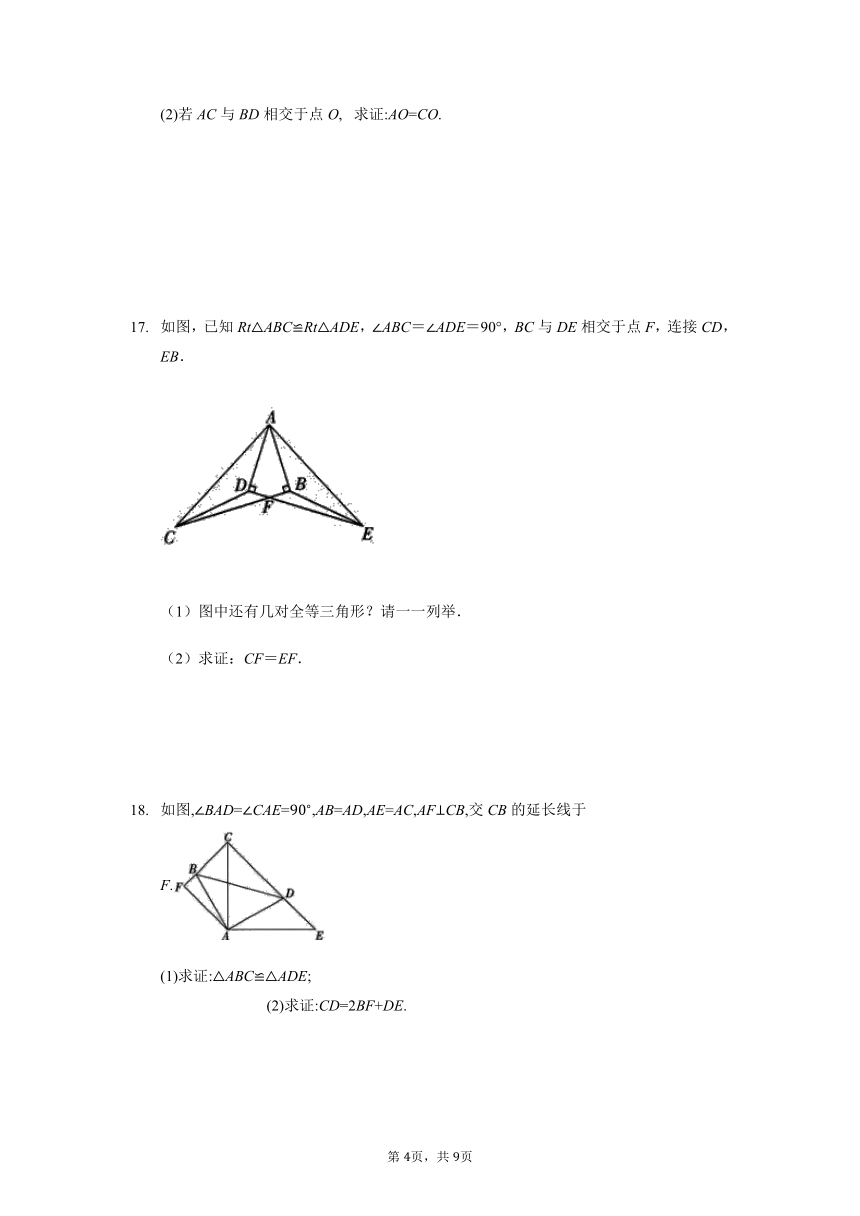
(2)若AC与BD相交于点O, 求证:AO=CO.
如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.
(1)图中还有几对全等三角形?请一一列举.
(2)求证:CF=EF.
如图,BAD=CAE=,AB=AD,AE=AC,AFCB,交CB的延长线于F.
(1)求证:ABCADE;
(2)求证:CD=2BF+DE.
参考答案
1.【答案】C
2.【答案】D
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】AB=CD(答案不唯一)
8.【答案】90°
9.【答案】 3
10.【答案】7
11.【答案】65
12.【答案】58
13.【答案】3或6
14.【答案】解:猜想:BF⊥AE.
理由:∵∠ACB=90°,
∴∠ACE=∠BCD=90°.
∴在Rt△BDC和Rt△AEC中,
,
∴Rt△BDC≌Rt△AEC(HL).
∴∠CBD=∠CAE.
又∠CAE+∠E=90°.
∴∠EBF+∠E=90°.
∴∠BFE=90°,
∴BF⊥AE.
15.【答案】证明:如图,连接AC.
CBAB,CDAD,
B=D=.
ABC和ADC均是直角三角形.
在RtABC和RtADC中,
RtABCRtADC(HL).
BC=DC.
E、F分别是BC、DC的中点,
BE=BC, DF=DC.
BE=DF.
在ABE和ADF中,
ABEADF(SAS).
AE=AF.
16.【答案】证明:(1)BE=DF,
BE-EF=DF-EF,即BF=DE.
AEBD,CFBD,AED=CFB=.
AD=BC,
RtADERtCBF(HL).
(2)如图,RtADERtCBF,AE=CF.
又AEBD,CFBD,AEO=CFO=.
AOE=COF,
AEOCFO(AAS),AO=CO.
17.【答案】(1)解:图中还有2对全等三角形;
△ADC≌△ABE,△CDF≌△EBF.
(2)证明:连接AF,
∵Rt△ABC≌Rt△ADE,
∴AB=AD,BC=DE,
又AF=AF,∠ABC=∠ADE=90°,
∴Rt△ABF≌Rt△ADF(HL),
∴BF=DF,
又BC=DE,
∴BC-BF=DE-DF,
即CF=EF.
18.【答案】证明:(1)BAD=CAE=,
BAC+CAD=,DAE+CAD=,
BAC=DAE.
在ABC和ADE中,
(2)如图,在CD上截取DG=BF,
ABCADE,
CBA=EDA,
FBA=GDA.
在AFB和AGD中,
,
AFCB,
AFB=AGD=,
AGC=.
在RtAFC和RtAGC中,
RtAFCRtAGC,
FC=GC.
由ABCADE,得BC=DE.
CD=GC+GD=FC+BF=CB+BF+BF=DE+2BF,即CD=2BF+DE.
第8页,共9页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共6小题,共18分)
下列条件中,不能判定两个直角三角形全等的是()
A. 一个锐角和斜边对应相等 B. 两条直角边对应相等
C. 两个锐角对应相等 D. 斜边和一条直角边对应相等
如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是()
A. B.
C. D.
如图,CEAB,DFAB,垂足分别为E、F,AF=BE,且AC=BD,则下列结论不一定正确的是( )
A. B.
C. D.
如图,AB⊥AC于点A,BD⊥CD于点D,若AC=DB,则下列结论中不正确的是()
A. B.
C. D.
如图,△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD和CE相交于O,AO的延长线交BC于F,则图中全等的直角三角形有()
A. 对 B. 对
C. 对 D. 对
如图,AD是ABC的角平分线,DFAB,垂足为F,DE=DG,ADG和AED的面积分别为50和39,则EDF的面积为( )
A. B. C. D.
二、填空题(本大题共7小题,共21分)
如图,已知AC⊥BD于点P,AP=CP,请增加一个条件,使△ABP≌△CDP(不能添加辅助线),你增加的条件是________.
如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE等于________.
如图,在RtABC中,C=,EDAB于点D,BC=BD.若AC=3cm,则AE+DE= cm.
如图,MNPQ,ABPQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB= .
如图,点D在边BC上,DE⊥AB,DF⊥BC,垂足分别为点E,D,BD=CF,BE=CD.若∠AFD=155°,则∠EDF=________°.
如图,在ABC中,ABC=,AB=CB,F为AB延长线上一点,点E在BC上,且AE=CF,若CAE=,则ACF的度数为 .
如图,有一个直角△ABC,∠C=90°,AC=6,BC=3,一条线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AD上运动,当AP=________时,以点P,A,Q为顶点的三角形与△ABC全等.
三、解答题(本大题共5小题,共61分)
如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.
如图,AB=AD,CBAB,CDAD,E、F分别是BC、DC的中点,连接AE、AF.求证:AE=AF.
如图,在四边形ABCD中,AD=BC,BE=DF,AEBD,CFBD,垂足分别为E、F.
(1)求证:ADECBF;
(2)若AC与BD相交于点O, 求证:AO=CO.
如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.
(1)图中还有几对全等三角形?请一一列举.
(2)求证:CF=EF.
如图,BAD=CAE=,AB=AD,AE=AC,AFCB,交CB的延长线于F.
(1)求证:ABCADE;
(2)求证:CD=2BF+DE.
参考答案
1.【答案】C
2.【答案】D
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】AB=CD(答案不唯一)
8.【答案】90°
9.【答案】 3
10.【答案】7
11.【答案】65
12.【答案】58
13.【答案】3或6
14.【答案】解:猜想:BF⊥AE.
理由:∵∠ACB=90°,
∴∠ACE=∠BCD=90°.
∴在Rt△BDC和Rt△AEC中,
,
∴Rt△BDC≌Rt△AEC(HL).
∴∠CBD=∠CAE.
又∠CAE+∠E=90°.
∴∠EBF+∠E=90°.
∴∠BFE=90°,
∴BF⊥AE.
15.【答案】证明:如图,连接AC.
CBAB,CDAD,
B=D=.
ABC和ADC均是直角三角形.
在RtABC和RtADC中,
RtABCRtADC(HL).
BC=DC.
E、F分别是BC、DC的中点,
BE=BC, DF=DC.
BE=DF.
在ABE和ADF中,
ABEADF(SAS).
AE=AF.
16.【答案】证明:(1)BE=DF,
BE-EF=DF-EF,即BF=DE.
AEBD,CFBD,AED=CFB=.
AD=BC,
RtADERtCBF(HL).
(2)如图,RtADERtCBF,AE=CF.
又AEBD,CFBD,AEO=CFO=.
AOE=COF,
AEOCFO(AAS),AO=CO.
17.【答案】(1)解:图中还有2对全等三角形;
△ADC≌△ABE,△CDF≌△EBF.
(2)证明:连接AF,
∵Rt△ABC≌Rt△ADE,
∴AB=AD,BC=DE,
又AF=AF,∠ABC=∠ADE=90°,
∴Rt△ABF≌Rt△ADF(HL),
∴BF=DF,
又BC=DE,
∴BC-BF=DE-DF,
即CF=EF.
18.【答案】证明:(1)BAD=CAE=,
BAC+CAD=,DAE+CAD=,
BAC=DAE.
在ABC和ADE中,
(2)如图,在CD上截取DG=BF,
ABCADE,
CBA=EDA,
FBA=GDA.
在AFB和AGD中,
,
AFCB,
AFB=AGD=,
AGC=.
在RtAFC和RtAGC中,
RtAFCRtAGC,
FC=GC.
由ABCADE,得BC=DE.
CD=GC+GD=FC+BF=CB+BF+BF=DE+2BF,即CD=2BF+DE.
第8页,共9页
