人教版八年级下册20.2 数据的波动程度-第1课时 方差 同步练习(word版含答案)
文档属性
| 名称 | 人教版八年级下册20.2 数据的波动程度-第1课时 方差 同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 337.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 07:07:55 | ||
图片预览

文档简介
八下-第二十章 数据的分析-20.2 数据的波动程度-第1课时 方差
一、选择题(共7小题;共35分)
1. 两名同学进行了 次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位的更稳定,通常还需要比较他们的成绩的
A. 众数 B. 中位数 C. 方差 D. 以上都不对
2. 在方差的计算公式 中,数字 和 分别表示
A. 数据的个数和方差 B. 平均数和数据个数
C. 数据的个数和平均数 D. 数据的方差和平均数
3. 为了解某社区居民的用电情况,随机对该社区 户居民进行了调查,下表是这 户居民 2014 年 4 月份用电量的调查结果:
那么关于这 户居民月用电量(单位:度),下列说法错误的是
A. 中位数是 度 B. 众数是 度
C. 方差是 D. 平均数是 度
4. 一组数据:,,,, 的平均数是 ,这组数据的方差为
A. B. C. D.
5. 在某中学举行的演讲比赛中,初一年级 名参赛选手的成绩如下表所示,请根据表中提供的数据,计算出这 名选手成绩的方差为
A. B. C. D.
6. 一次数学测试,某小组五名同学的成绩如下表所示(有两个数据被遮盖).那么被遮盖的两个数据依次是
A. , B. , C. , D. ,
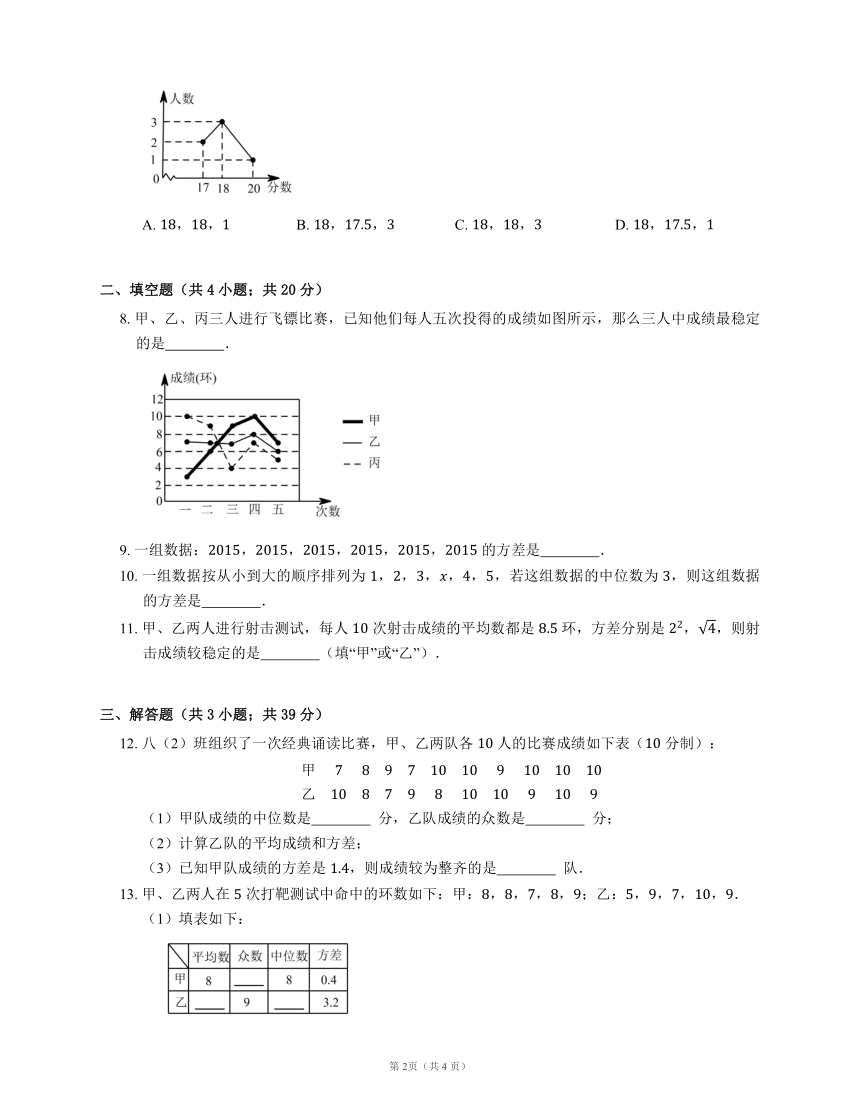
7. 在 2014 年的体育测试中,某校 名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是
A. ,, B. ,, C. ,, D. ,,
二、填空题(共4小题;共20分)
8. 甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图所示,那么三人中成绩最稳定的是 .
9. 一组数据:,,,,, 的方差是 .
10. 一组数据按从小到大的顺序排列为 ,,,,,,若这组数据的中位数为 ,则这组数据的方差是 .
11. 甲、乙两人进行射击测试,每人 次射击成绩的平均数都是 环,方差分别是 ,,则射击成绩较稳定的是 (填“甲”或“乙”).
三、解答题(共3小题;共39分)
12. 八(2)班组织了一次经典诵读比赛,甲、乙两队各 人的比赛成绩如下表( 分制):
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是 ,则成绩较为整齐的是 队.
13. 甲、乙两人在 次打靶测试中命中的环数如下:甲:,,,,;乙:,,,,.
(1)填表如下:
(2)教练根据这 次成绩,选择甲参加射击比赛,教练的理由是什么
(3)如果乙再射击 次,命中 环,那么乙射击成绩的方差将 (填“变大““变小“或“不变”)
14. 为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两人在相同条件下各射靶 次,为了比较两人的成绩,制作了如下统计图表:
(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出 说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则
答案
第一部分
1. C
2. C
3. C
4. A
5. B
6. C
7. A
第二部分
8. 乙
9.
10.
【解析】由题意可知,,所以平均数为 ,则可求方差.
11. 乙
第三部分
12. (1) ;.
(2) 分;.
(3) 乙.
13. (1) 甲:;乙:;.
(2) 甲与乙的平均成绩相同,但甲的方差比较小,说明甲的成绩比较稳定,故选甲.
(3) 变小.
14. (1)
(2) 甲应胜出.理由:平均数相同,甲的方差小于乙的方差,故甲较稳定,所以甲应胜出.
(3) 若希望乙胜出,则评判规则应为中位数较大者胜出(答案不唯一).
第1页(共1 页)
一、选择题(共7小题;共35分)
1. 两名同学进行了 次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位的更稳定,通常还需要比较他们的成绩的
A. 众数 B. 中位数 C. 方差 D. 以上都不对
2. 在方差的计算公式 中,数字 和 分别表示
A. 数据的个数和方差 B. 平均数和数据个数
C. 数据的个数和平均数 D. 数据的方差和平均数
3. 为了解某社区居民的用电情况,随机对该社区 户居民进行了调查,下表是这 户居民 2014 年 4 月份用电量的调查结果:
那么关于这 户居民月用电量(单位:度),下列说法错误的是
A. 中位数是 度 B. 众数是 度
C. 方差是 D. 平均数是 度
4. 一组数据:,,,, 的平均数是 ,这组数据的方差为
A. B. C. D.
5. 在某中学举行的演讲比赛中,初一年级 名参赛选手的成绩如下表所示,请根据表中提供的数据,计算出这 名选手成绩的方差为
A. B. C. D.
6. 一次数学测试,某小组五名同学的成绩如下表所示(有两个数据被遮盖).那么被遮盖的两个数据依次是
A. , B. , C. , D. ,
7. 在 2014 年的体育测试中,某校 名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是
A. ,, B. ,, C. ,, D. ,,
二、填空题(共4小题;共20分)
8. 甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图所示,那么三人中成绩最稳定的是 .
9. 一组数据:,,,,, 的方差是 .
10. 一组数据按从小到大的顺序排列为 ,,,,,,若这组数据的中位数为 ,则这组数据的方差是 .
11. 甲、乙两人进行射击测试,每人 次射击成绩的平均数都是 环,方差分别是 ,,则射击成绩较稳定的是 (填“甲”或“乙”).
三、解答题(共3小题;共39分)
12. 八(2)班组织了一次经典诵读比赛,甲、乙两队各 人的比赛成绩如下表( 分制):
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是 ,则成绩较为整齐的是 队.
13. 甲、乙两人在 次打靶测试中命中的环数如下:甲:,,,,;乙:,,,,.
(1)填表如下:
(2)教练根据这 次成绩,选择甲参加射击比赛,教练的理由是什么
(3)如果乙再射击 次,命中 环,那么乙射击成绩的方差将 (填“变大““变小“或“不变”)
14. 为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两人在相同条件下各射靶 次,为了比较两人的成绩,制作了如下统计图表:
(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出 说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则
答案
第一部分
1. C
2. C
3. C
4. A
5. B
6. C
7. A
第二部分
8. 乙
9.
10.
【解析】由题意可知,,所以平均数为 ,则可求方差.
11. 乙
第三部分
12. (1) ;.
(2) 分;.
(3) 乙.
13. (1) 甲:;乙:;.
(2) 甲与乙的平均成绩相同,但甲的方差比较小,说明甲的成绩比较稳定,故选甲.
(3) 变小.
14. (1)
(2) 甲应胜出.理由:平均数相同,甲的方差小于乙的方差,故甲较稳定,所以甲应胜出.
(3) 若希望乙胜出,则评判规则应为中位数较大者胜出(答案不唯一).
第1页(共1 页)
