人教版数学八年级下第二十章 数据的分析自我综合评价(word版含答案)
文档属性
| 名称 | 人教版数学八年级下第二十章 数据的分析自我综合评价(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 619.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 09:41:00 | ||
图片预览

文档简介
八下-第二十章 数据的分析-自我综合评价
一、选择题(共7小题;共35分)
1. 名学生进行 秒钟跳绳测试,测试成绩统计如下表:
则这次测试成绩的中位数 满足
A. B. C. D.
2. 李华根据演讲比赛中九位评委所给的分数制作了如下表格:
如果要去掉一个最高分和一个最低分,则表中数据一定不发生变化的是
A. 平均数 B. 众数 C. 方差 D. 中位数
3. 实施新课改以来,某班学生经常采用“小组合作学习”的方式进行学习.值周班长小兵每周对各小组合作学习的情况进行综合评分.下表是其中一周的评分结果:
“分值”这组数据的中位数和众数分别是
A. , B. , C. , D. ,
4. 若干名工人某天生产同一种零件,将生产的零件数整理成条形统计图,如图所示.设他们生产的零件数的平均数为 ,中位数为 ,众数为 ,则
A. B. C. D.
5. 若一个样本的方差为 ,则这个样本的容量为
A. B. C. D.
6. 下列叙述不正确的个数是
①一组数据的平均数和中位数一定相等;
②一组数据的方差总大于 ;
③一组数据的中位数可能有两个;
④一组数据的众数可能有多个.
A. B. C. D.
7. 某校四个绿化小组一天植树的棵数如下:,,, .已知这组数据的众数与平均数相等,则这组数据的中位数是
A. B. C. D.
二、填空题(共5小题;共25分)
8. 某中学随机抽查了 名学生,了解他们一周的课外阅读时间,结果如下表所示:
则这 名学生一周的平均课外阅读时间是 小时.
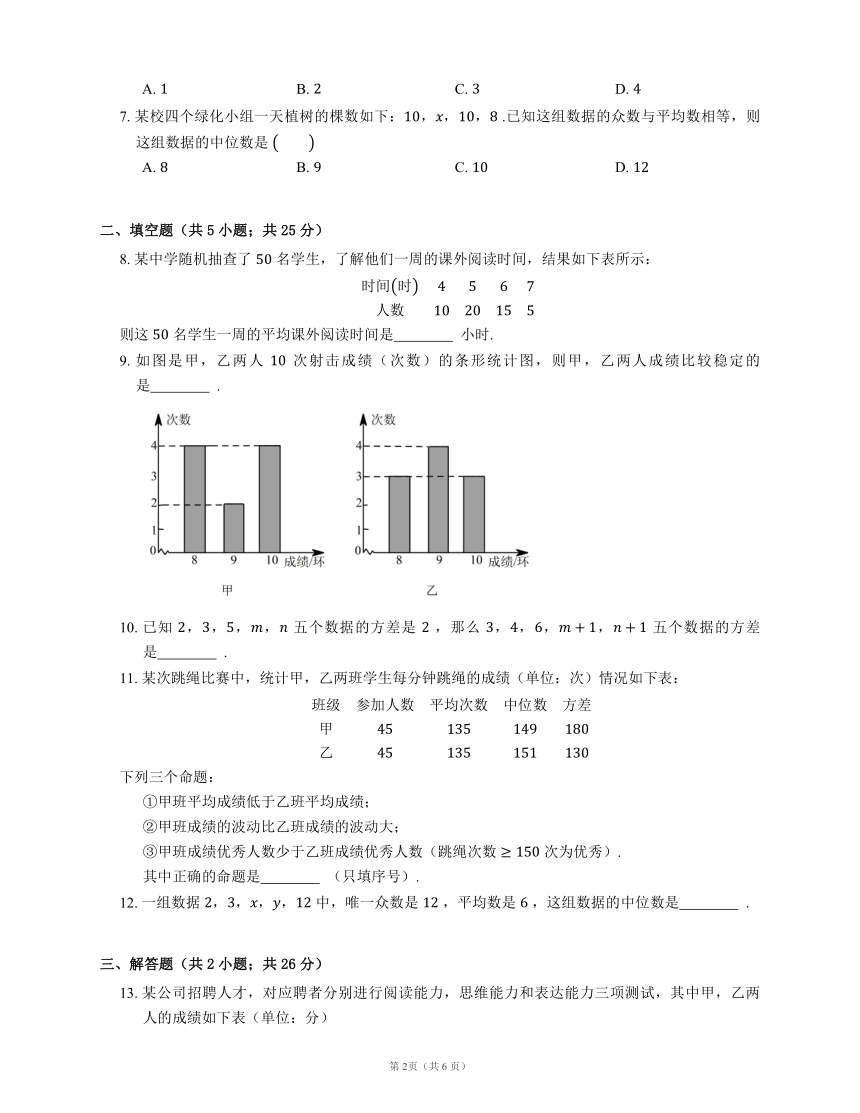
9. 如图是甲,乙两人 次射击成绩(次数)的条形统计图,则甲,乙两人成绩比较稳定的是 .
10. 已知 ,,,, 五个数据的方差是 ,那么 ,,,, 五个数据的方差是 .
11. 某次跳绳比赛中,统计甲,乙两班学生每分钟跳绳的成绩(单位:次)情况如下表:
下列三个命题:
①甲班平均成绩低于乙班平均成绩;
②甲班成绩的波动比乙班成绩的波动大;
③甲班成绩优秀人数少于乙班成绩优秀人数(跳绳次数 次为优秀).
其中正确的命题是 (只填序号).
12. 一组数据 ,,,, 中,唯一众数是 ,平均数是 ,这组数据的中位数是 .
三、解答题(共2小题;共26分)
13. 某公司招聘人才,对应聘者分别进行阅读能力,思维能力和表达能力三项测试,其中甲,乙两人的成绩如下表(单位:分)
(1)若根据三项测试的平均成绩在甲,乙两人中录用一人,那么谁将被录用
(2)根据实际需要,公司将阅读,思维和表达能力三项测试得分按 的比例确定每人的最后成绩,若按此成绩在甲,乙两人中录用一人,谁将被录用
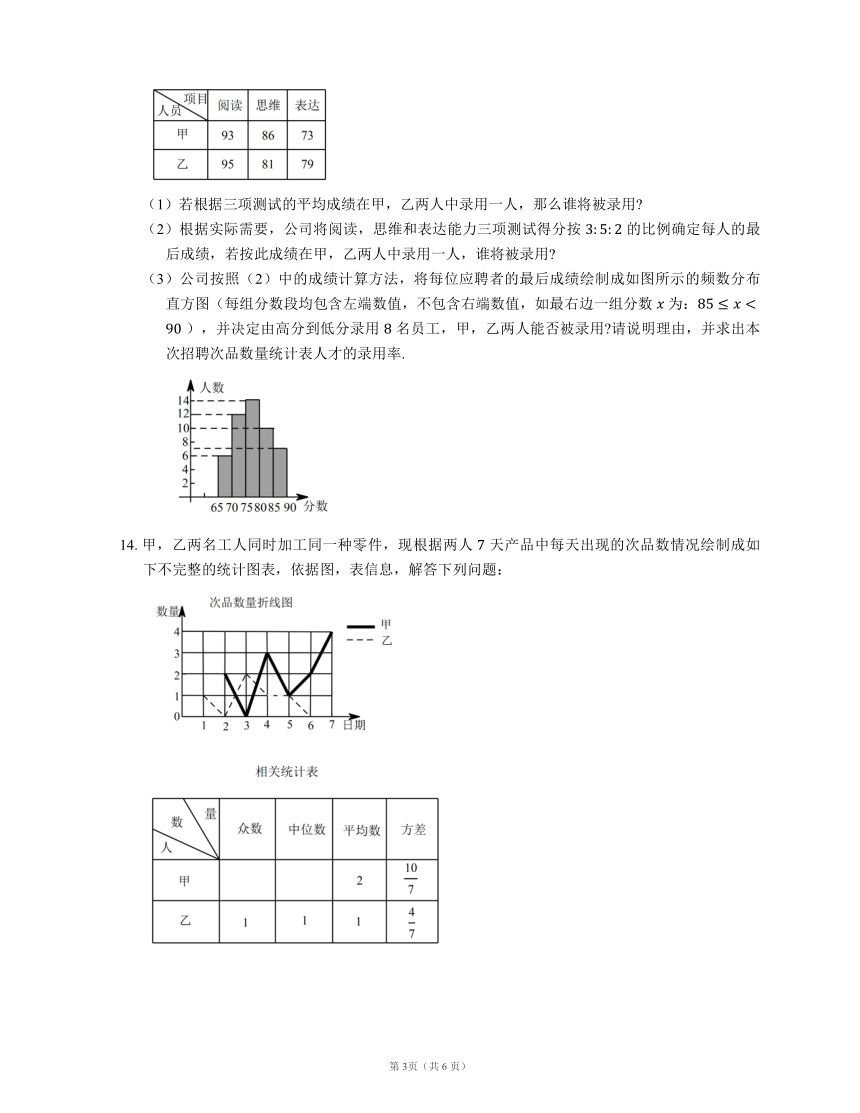
(3)公司按照(2)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最右边一组分数 为: ),并决定由高分到低分录用 名员工,甲,乙两人能否被录用 请说明理由,并求出本次招聘次品数量统计表人才的录用率.
14. 甲,乙两名工人同时加工同一种零件,现根据两人 天产品中每天出现的次品数情况绘制成如下不完整的统计图表,依据图,表信息,解答下列问题:
(1)请补全图,表;
(2)判断谁出现次品的波动较小;
(3)估计乙加工该种零件 天出现次品多少件
答案
第一部分
1. B
2. D
3. B
4. D
5. A
6. C
7. C
第二部分
8.
9. 乙
10.
11. ②③
12.
第三部分
13. (1) 甲的平均成绩是:(分)
乙的平均成绩是:(分)
乙将被录用
(2) 甲的成绩是:(分)
乙的成绩是:(分)
甲将被录用
(3) 甲一定被录用,而乙不一定能被录用 .
理由如下:
由直方图知成绩最高一组分数段 中有 人,公司招聘 人,因为 分,显然甲在该组,所以甲一定能被录用;
在 这一组内有 人,仅有 人能被录用,而 分,在这一段内不一定是最高分,所以乙不一定能被录用.
由直方图知,应聘人数共有 人,录用人数为 人,
本次招聘人才的录用率为
14. (1)
(2) , .
乙出现次品的波动较小
(3) 乙加工该种零件 天出现次品约 件.
第1页(共1 页)
一、选择题(共7小题;共35分)
1. 名学生进行 秒钟跳绳测试,测试成绩统计如下表:
则这次测试成绩的中位数 满足
A. B. C. D.
2. 李华根据演讲比赛中九位评委所给的分数制作了如下表格:
如果要去掉一个最高分和一个最低分,则表中数据一定不发生变化的是
A. 平均数 B. 众数 C. 方差 D. 中位数
3. 实施新课改以来,某班学生经常采用“小组合作学习”的方式进行学习.值周班长小兵每周对各小组合作学习的情况进行综合评分.下表是其中一周的评分结果:
“分值”这组数据的中位数和众数分别是
A. , B. , C. , D. ,
4. 若干名工人某天生产同一种零件,将生产的零件数整理成条形统计图,如图所示.设他们生产的零件数的平均数为 ,中位数为 ,众数为 ,则
A. B. C. D.
5. 若一个样本的方差为 ,则这个样本的容量为
A. B. C. D.
6. 下列叙述不正确的个数是
①一组数据的平均数和中位数一定相等;
②一组数据的方差总大于 ;
③一组数据的中位数可能有两个;
④一组数据的众数可能有多个.
A. B. C. D.
7. 某校四个绿化小组一天植树的棵数如下:,,, .已知这组数据的众数与平均数相等,则这组数据的中位数是
A. B. C. D.
二、填空题(共5小题;共25分)
8. 某中学随机抽查了 名学生,了解他们一周的课外阅读时间,结果如下表所示:
则这 名学生一周的平均课外阅读时间是 小时.
9. 如图是甲,乙两人 次射击成绩(次数)的条形统计图,则甲,乙两人成绩比较稳定的是 .
10. 已知 ,,,, 五个数据的方差是 ,那么 ,,,, 五个数据的方差是 .
11. 某次跳绳比赛中,统计甲,乙两班学生每分钟跳绳的成绩(单位:次)情况如下表:
下列三个命题:
①甲班平均成绩低于乙班平均成绩;
②甲班成绩的波动比乙班成绩的波动大;
③甲班成绩优秀人数少于乙班成绩优秀人数(跳绳次数 次为优秀).
其中正确的命题是 (只填序号).
12. 一组数据 ,,,, 中,唯一众数是 ,平均数是 ,这组数据的中位数是 .
三、解答题(共2小题;共26分)
13. 某公司招聘人才,对应聘者分别进行阅读能力,思维能力和表达能力三项测试,其中甲,乙两人的成绩如下表(单位:分)
(1)若根据三项测试的平均成绩在甲,乙两人中录用一人,那么谁将被录用
(2)根据实际需要,公司将阅读,思维和表达能力三项测试得分按 的比例确定每人的最后成绩,若按此成绩在甲,乙两人中录用一人,谁将被录用
(3)公司按照(2)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最右边一组分数 为: ),并决定由高分到低分录用 名员工,甲,乙两人能否被录用 请说明理由,并求出本次招聘次品数量统计表人才的录用率.
14. 甲,乙两名工人同时加工同一种零件,现根据两人 天产品中每天出现的次品数情况绘制成如下不完整的统计图表,依据图,表信息,解答下列问题:
(1)请补全图,表;
(2)判断谁出现次品的波动较小;
(3)估计乙加工该种零件 天出现次品多少件
答案
第一部分
1. B
2. D
3. B
4. D
5. A
6. C
7. C
第二部分
8.
9. 乙
10.
11. ②③
12.
第三部分
13. (1) 甲的平均成绩是:(分)
乙的平均成绩是:(分)
乙将被录用
(2) 甲的成绩是:(分)
乙的成绩是:(分)
甲将被录用
(3) 甲一定被录用,而乙不一定能被录用 .
理由如下:
由直方图知成绩最高一组分数段 中有 人,公司招聘 人,因为 分,显然甲在该组,所以甲一定能被录用;
在 这一组内有 人,仅有 人能被录用,而 分,在这一段内不一定是最高分,所以乙不一定能被录用.
由直方图知,应聘人数共有 人,录用人数为 人,
本次招聘人才的录用率为
14. (1)
(2) , .
乙出现次品的波动较小
(3) 乙加工该种零件 天出现次品约 件.
第1页(共1 页)
