人教版数学八年级下册第十八章 平行四边形自我综合评价试卷(word解析版)
文档属性
| 名称 | 人教版数学八年级下册第十八章 平行四边形自我综合评价试卷(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 492.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 09:56:57 | ||
图片预览

文档简介
八下-第十八章 平行四边形-自我综合评价(三)
一、选择题(共7小题;共35分)
1. 如图,菱形 的对角线 , 相交于 点,, 分别是 , 边上的中点,连接 ,若 ,,则菱形 的周长为
A. B. C. D.
2. 如图,在平行四边形 中, 与 相交于点 ,则下列结论不一定成立的是
A. B.
C. D.
3. 如图,将矩形 沿 折叠,若 ,则 等于
A. B. C. D.
4. 如图, 是 的中位线,若 ,,,则 的周长是
A. B. C. D.
5. 在平面直角坐标系中,已知点 ,,,,则以这四个点为顶点的四边形 是
A. 矩形 B. 菱形
C. 正方形 D. 一般的平行四边形
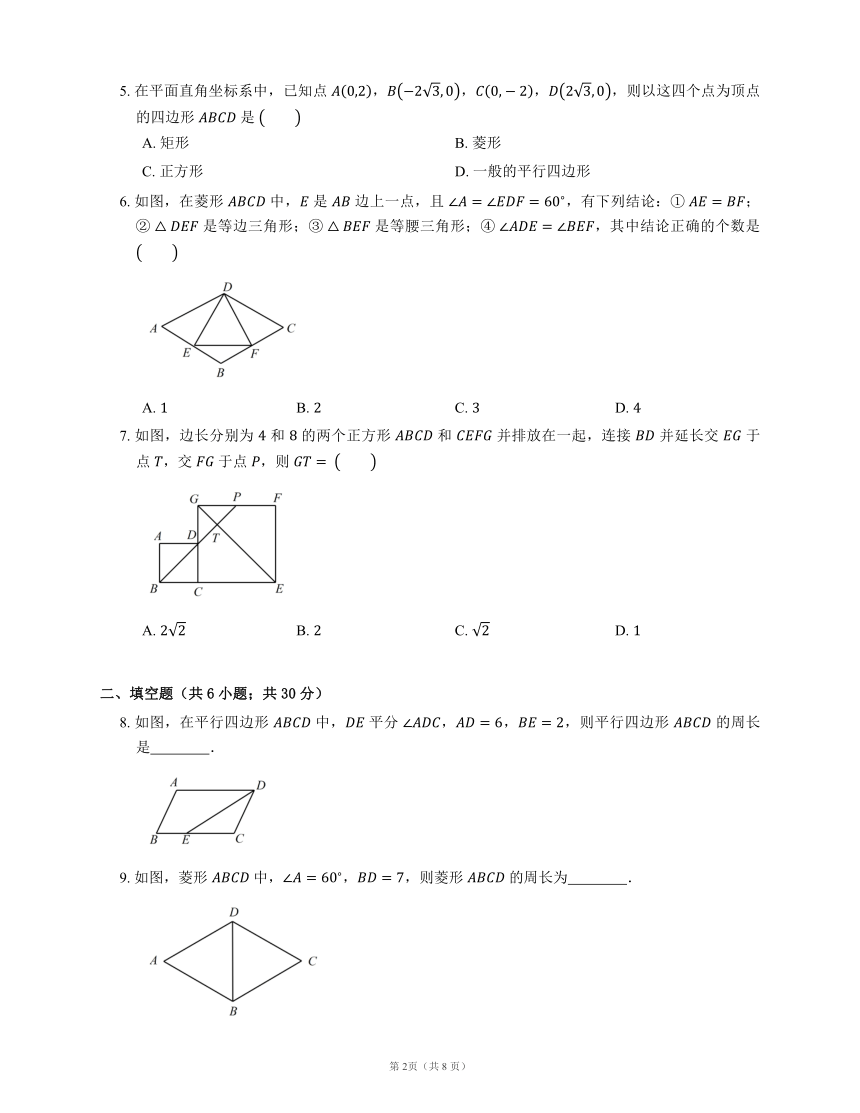
6. 如图,在菱形 中, 是 边上一点,且 ,有下列结论:① ;② 是等边三角形;③ 是等腰三角形;④ ,其中结论正确的个数是
A. B. C. D.
7. 如图,边长分别为 和 的两个正方形 和 并排放在一起,连接 并延长交 于点 ,交 于点 ,则
A. B. C. D.
二、填空题(共6小题;共30分)
8. 如图,在平行四边形 中, 平分 ,,,则平行四边形 的周长是 .
9. 如图,菱形 中,,,则菱形 的周长为 .
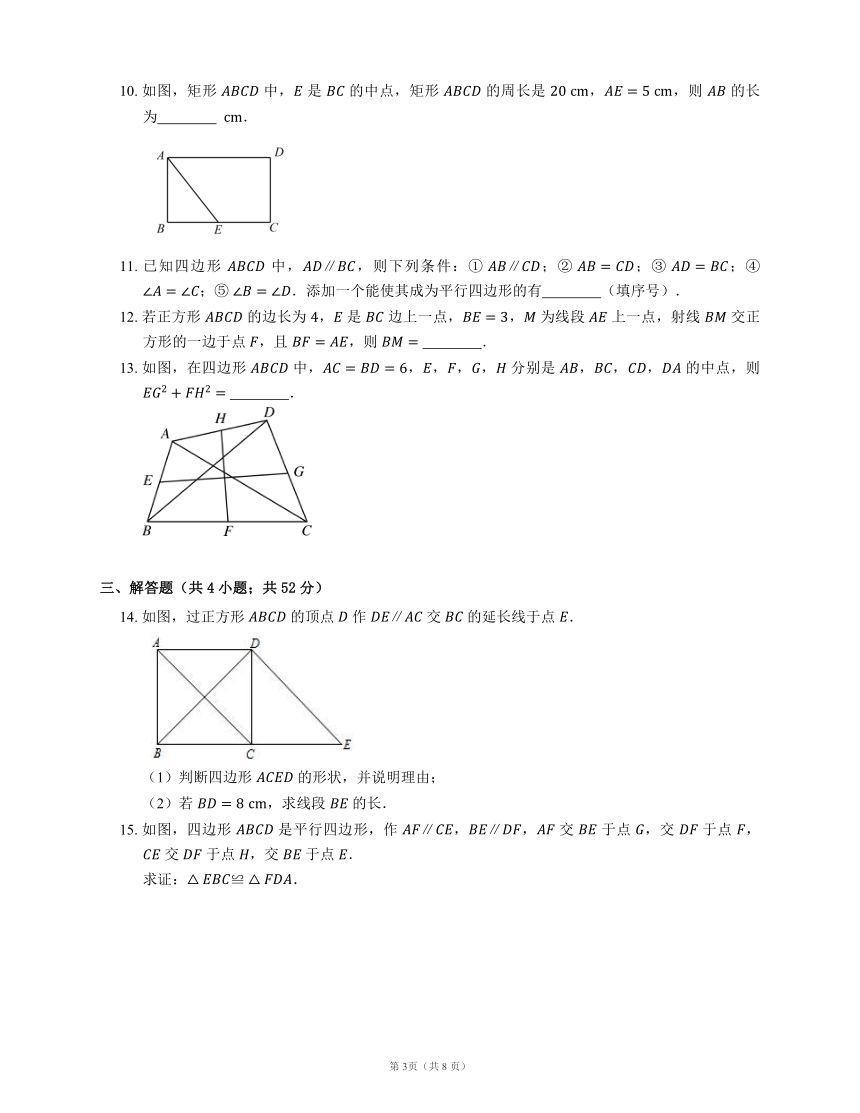
10. 如图,矩形 中, 是 的中点,矩形 的周长是 ,,则 的长为 .
11. 已知四边形 中,,则下列条件:① ;② ;③ ;④ ;⑤ .添加一个能使其成为平行四边形的有 (填序号).
12. 若正方形 的边长为 , 是 边上一点,, 为线段 上一点,射线 交正方形的一边于点 ,且 ,则 .
13. 如图,在四边形 中,,,,, 分别是 ,,, 的中点,则 .
三、解答题(共4小题;共52分)
14. 如图,过正方形 的顶点 作 交 的延长线于点 .
(1)判断四边形 的形状,并说明理由;
(2)若 ,求线段 的长.
15. 如图,四边形 是平行四边形,作 ,, 交 于点 ,交 于点 , 交 于点 ,交 于点 .
求证:.
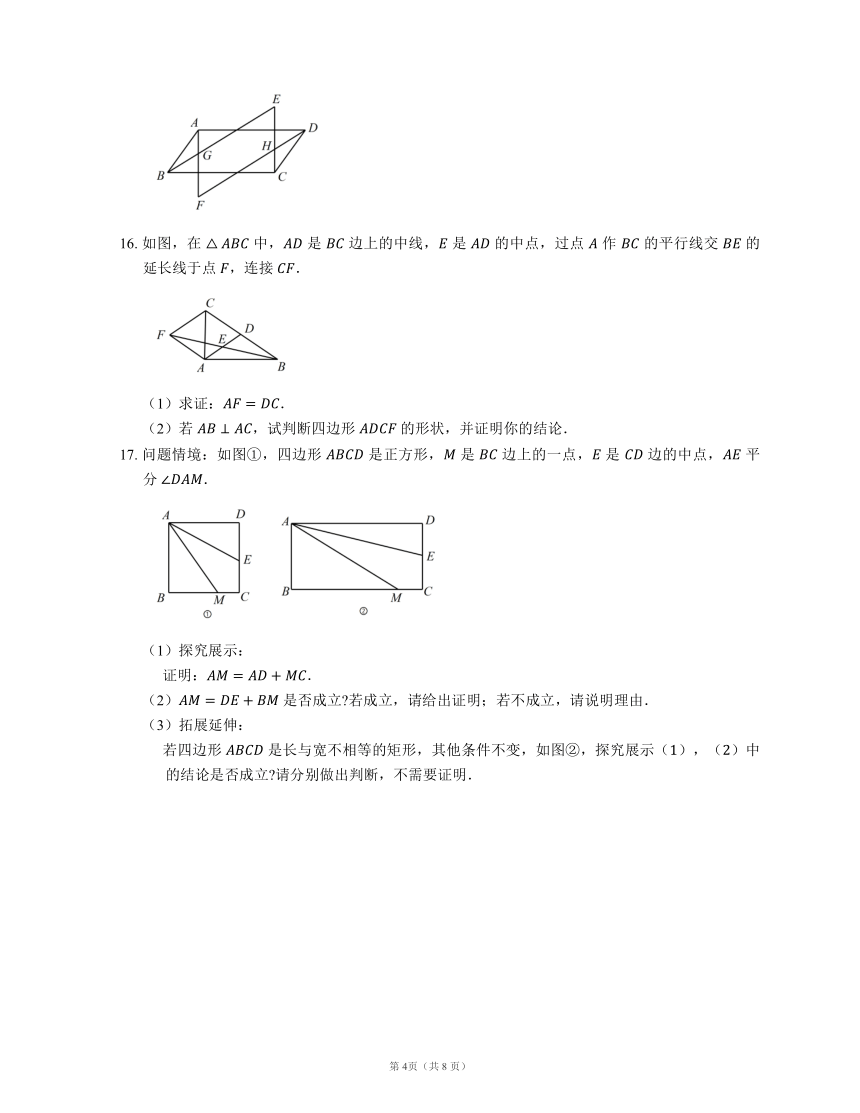
16. 如图,在 中, 是 边上的中线, 是 的中点,过点 作 的平行线交 的延长线于点 ,连接 .
(1)求证:.
(2)若 ,试判断四边形 的形状,并证明你的结论.
17. 问题情境:如图①,四边形 是正方形, 是 边上的一点, 是 边的中点, 平分 .
(1)探究展示:
证明:.
(2) 是否成立 若成立,请给出证明;若不成立,请说明理由.
(3)拓展延伸:
若四边形 是长与宽不相等的矩形,其他条件不变,如图②,探究展示(),()中的结论是否成立 请分别做出判断,不需要证明.
答案
第一部分
1. C 【解析】 , 分别是 , 边上的中点,
.
菱形 的对角线 , 相交于点 ,
,,.
在 中,,
菱形 的周长为 .
2. D
3. C
4. B
5. B
6. C 【解析】提示:
连接 .证明 .
7. A 【解析】提示:点 是 的中点.
第二部分
8.
9.
10.
11. ①③④⑤
12. 或
【解析】提示:
① , .
② .
13.
第三部分
14. (1) 四边形 是平行四边形.理由如下:
四边形 是正方形,
,即 .
,
四边形 是平行四边形.
(2) 由(1)知,,
,
,
.
15. 设 与 的交点为 , 与 的交点为 .
,,
四边形 是平行四边形,
.
,,
四边形 是平行四边形,
.
在平行四边形 中,,
.
16. (1) 是 的中点,
.
,
,.
.
.
是 边上的中线,
,
.
(2) 四边形 是菱形.
由(1)知, .
,
四边形 是平行四边形.
又 ,
是直角三角形.
是 边上的中线,
.
平行四边形 是菱形.
17. (1) 延长 , 交于点 ,如图所示:
四边形 是正方形,
.
.
在 和 中,
.
.
平分 ,
.
.
.
.
(2) 成立.
过点 作 ,交 的延长线于点 ,如图所示.
四边形 是正方形.
,,.
,
.
.
在 和 中,
.
,.
,
.
,
.
.
.
.
(3) ()成立;()不成立.
第1页(共1 页)
一、选择题(共7小题;共35分)
1. 如图,菱形 的对角线 , 相交于 点,, 分别是 , 边上的中点,连接 ,若 ,,则菱形 的周长为
A. B. C. D.
2. 如图,在平行四边形 中, 与 相交于点 ,则下列结论不一定成立的是
A. B.
C. D.
3. 如图,将矩形 沿 折叠,若 ,则 等于
A. B. C. D.
4. 如图, 是 的中位线,若 ,,,则 的周长是
A. B. C. D.
5. 在平面直角坐标系中,已知点 ,,,,则以这四个点为顶点的四边形 是
A. 矩形 B. 菱形
C. 正方形 D. 一般的平行四边形
6. 如图,在菱形 中, 是 边上一点,且 ,有下列结论:① ;② 是等边三角形;③ 是等腰三角形;④ ,其中结论正确的个数是
A. B. C. D.
7. 如图,边长分别为 和 的两个正方形 和 并排放在一起,连接 并延长交 于点 ,交 于点 ,则
A. B. C. D.
二、填空题(共6小题;共30分)
8. 如图,在平行四边形 中, 平分 ,,,则平行四边形 的周长是 .
9. 如图,菱形 中,,,则菱形 的周长为 .
10. 如图,矩形 中, 是 的中点,矩形 的周长是 ,,则 的长为 .
11. 已知四边形 中,,则下列条件:① ;② ;③ ;④ ;⑤ .添加一个能使其成为平行四边形的有 (填序号).
12. 若正方形 的边长为 , 是 边上一点,, 为线段 上一点,射线 交正方形的一边于点 ,且 ,则 .
13. 如图,在四边形 中,,,,, 分别是 ,,, 的中点,则 .
三、解答题(共4小题;共52分)
14. 如图,过正方形 的顶点 作 交 的延长线于点 .
(1)判断四边形 的形状,并说明理由;
(2)若 ,求线段 的长.
15. 如图,四边形 是平行四边形,作 ,, 交 于点 ,交 于点 , 交 于点 ,交 于点 .
求证:.
16. 如图,在 中, 是 边上的中线, 是 的中点,过点 作 的平行线交 的延长线于点 ,连接 .
(1)求证:.
(2)若 ,试判断四边形 的形状,并证明你的结论.
17. 问题情境:如图①,四边形 是正方形, 是 边上的一点, 是 边的中点, 平分 .
(1)探究展示:
证明:.
(2) 是否成立 若成立,请给出证明;若不成立,请说明理由.
(3)拓展延伸:
若四边形 是长与宽不相等的矩形,其他条件不变,如图②,探究展示(),()中的结论是否成立 请分别做出判断,不需要证明.
答案
第一部分
1. C 【解析】 , 分别是 , 边上的中点,
.
菱形 的对角线 , 相交于点 ,
,,.
在 中,,
菱形 的周长为 .
2. D
3. C
4. B
5. B
6. C 【解析】提示:
连接 .证明 .
7. A 【解析】提示:点 是 的中点.
第二部分
8.
9.
10.
11. ①③④⑤
12. 或
【解析】提示:
① , .
② .
13.
第三部分
14. (1) 四边形 是平行四边形.理由如下:
四边形 是正方形,
,即 .
,
四边形 是平行四边形.
(2) 由(1)知,,
,
,
.
15. 设 与 的交点为 , 与 的交点为 .
,,
四边形 是平行四边形,
.
,,
四边形 是平行四边形,
.
在平行四边形 中,,
.
16. (1) 是 的中点,
.
,
,.
.
.
是 边上的中线,
,
.
(2) 四边形 是菱形.
由(1)知, .
,
四边形 是平行四边形.
又 ,
是直角三角形.
是 边上的中线,
.
平行四边形 是菱形.
17. (1) 延长 , 交于点 ,如图所示:
四边形 是正方形,
.
.
在 和 中,
.
.
平分 ,
.
.
.
.
(2) 成立.
过点 作 ,交 的延长线于点 ,如图所示.
四边形 是正方形.
,,.
,
.
.
在 和 中,
.
,.
,
.
,
.
.
.
.
(3) ()成立;()不成立.
第1页(共1 页)
