人教版八年级下册19.1.2 函数的图象-第1课时 函数的图象及其画法 同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册19.1.2 函数的图象-第1课时 函数的图象及其画法 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-15 17:14:13 | ||
图片预览

文档简介
八下-第十九章 一次函数-19.1 函数-19.1.2 函数的图象-第1课时 函数的图象及其画法
一、选择题(共6小题;共30分)
1. 下列四点中,在函数 的图象上的是
A. B. C. D.
2. 已知点 在函数 的图象上,则
A. B. C. D.
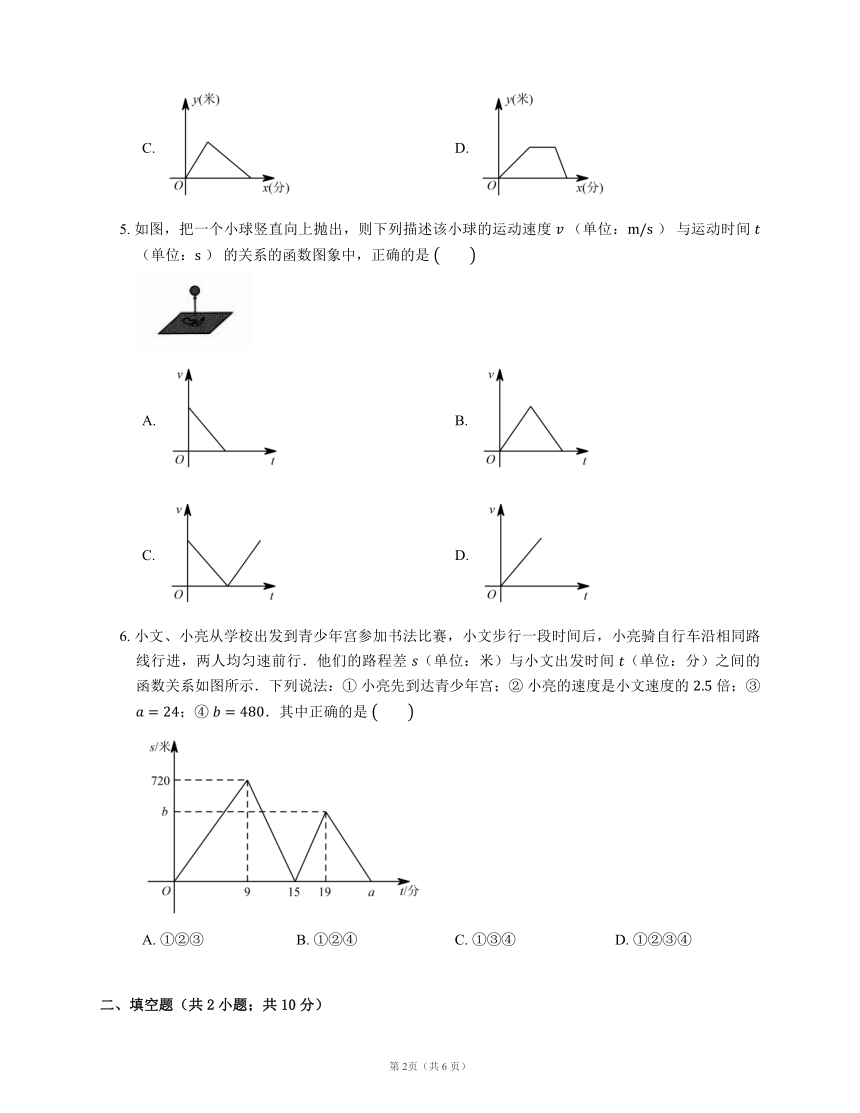
3. 如图是某市某一 天内的气温变化图,根据图象,下列说法中错误的是
A. 这一 天中最高气温是
B. 这一 天中最高气温与最低气温的差为
C. 这一 天中 时至 时之间的气温在逐渐升高
D. 这一天中只有 时至 时之间的气温在逐渐降低
4. 小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会儿太极拳,然后沿原路漫步走到家,下面能反映当天爷爷离家的距离 (米)与时间 (分)之间关系的大致图象是
A. B.
C. D.
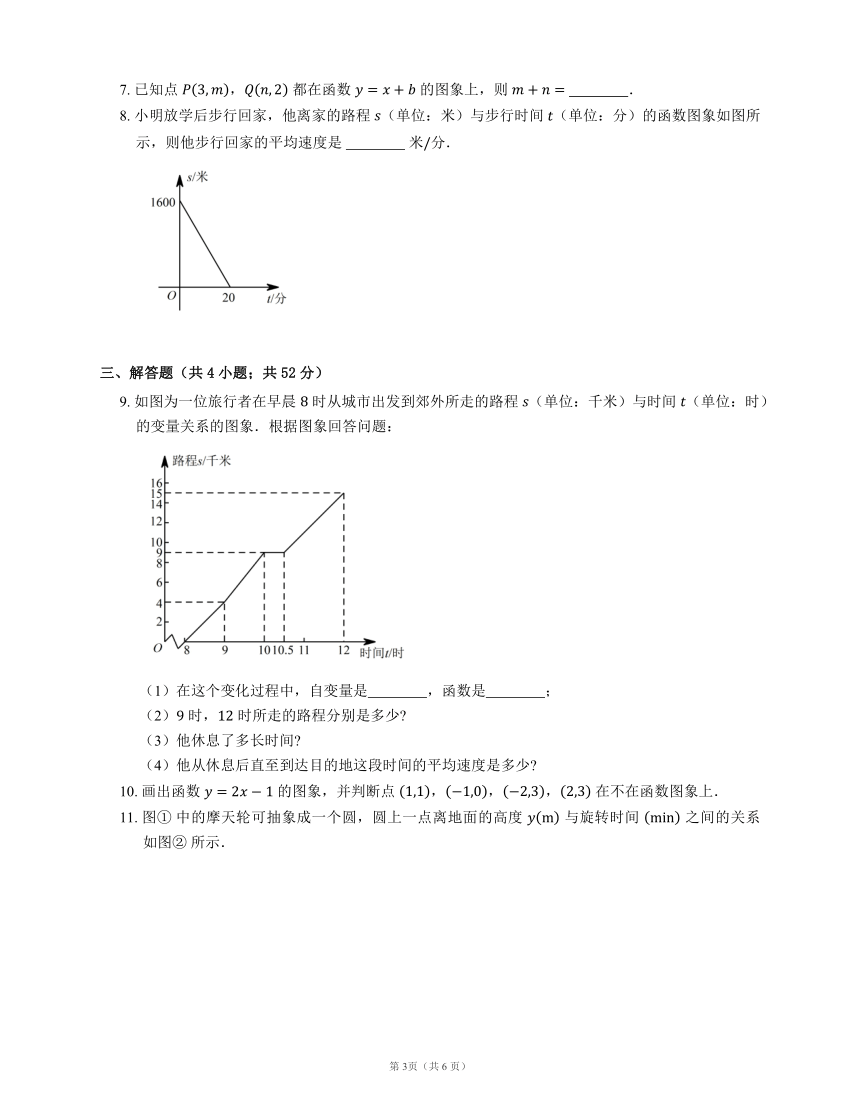
5. 如图,把一个小球竖直向上抛出,则下列描述该小球的运动速度 (单位: ) 与运动时间 (单位: ) 的关系的函数图象中,正确的是
A. B.
C. D.
6. 小文、小亮从学校出发到青少年宫参加书法比赛,小文步行一段时间后,小亮骑自行车沿相同路线行进,两人均匀速前行.他们的路程差 (单位:米)与小文出发时间 (单位:分)之间的函数关系如图所示.下列说法:① 小亮先到达青少年宫;② 小亮的速度是小文速度的 倍;③ ;④ .其中正确的是
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
二、填空题(共2小题;共10分)
7. 已知点 , 都在函数 的图象上,则 .
8. 小明放学后步行回家,他离家的路程 (单位:米)与步行时间 (单位:分)的函数图象如图所示,则他步行回家的平均速度是 .
三、解答题(共4小题;共52分)
9. 如图为一位旅行者在早晨 时从城市出发到郊外所走的路程 (单位:千米)与时间 (单位:时)的变量关系的图象.根据图象回答问题:
(1)在这个变化过程中,自变量是 ,函数是 ;
(2) 时, 时所走的路程分别是多少
(3)他休息了多长时间
(4)他从休息后直至到达目的地这段时间的平均速度是多少
10. 画出函数 的图象,并判断点 ,,, 在不在函数图象上.
11. 图① 中的摩天轮可抽象成一个圆,圆上一点离地面的高度 与旋转时间 之间的关系如图② 所示.
(1)根据图② 填表:
(2)变量 是 的函数吗 为什么
(3)根据图中的信息,请写出摩天轮的直径.
12. (1)画出函数 的图象;
(2)试判断点 是否在上述函数图象上.
答案
第一部分
1. C
2. A
3. D
4. B
5. C
6. B 【解析】根据图象知,小文步行 分钟时,小亮开始出发, 分钟时两人相遇,之后小亮超过小文,在 分钟时,小亮到达目的地, 分钟时,小文到达目的地.
小文的速度 (米 /秒),小亮的速度 (米 /秒) .
(米);
(秒).
第二部分
7.
8.
第三部分
9. (1) 时间 ;路程 .
(2) 时, 时所走的路程分别是 千米, 千米.
(3) 该旅行者休息的时间为 小时.
(4) 他从休息后直至到达目的地这段时间的平均速度是 .
10. 函数图象如图:
点 , 在函数 的图象上,点 , 不在函数 的图象上.
11. (1)
(2) 是 的函数.由图象可知,变量 随着 的变化而变化,同时对于每一个 ,按照图象,都有唯一的变量 与之相对应,符合函数的定义.
(3) 摩天轮的直径是 .
12. (1)
(2) 点 不在函数 的图象上.
第1页(共1 页)
一、选择题(共6小题;共30分)
1. 下列四点中,在函数 的图象上的是
A. B. C. D.
2. 已知点 在函数 的图象上,则
A. B. C. D.
3. 如图是某市某一 天内的气温变化图,根据图象,下列说法中错误的是
A. 这一 天中最高气温是
B. 这一 天中最高气温与最低气温的差为
C. 这一 天中 时至 时之间的气温在逐渐升高
D. 这一天中只有 时至 时之间的气温在逐渐降低
4. 小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会儿太极拳,然后沿原路漫步走到家,下面能反映当天爷爷离家的距离 (米)与时间 (分)之间关系的大致图象是
A. B.
C. D.
5. 如图,把一个小球竖直向上抛出,则下列描述该小球的运动速度 (单位: ) 与运动时间 (单位: ) 的关系的函数图象中,正确的是
A. B.
C. D.
6. 小文、小亮从学校出发到青少年宫参加书法比赛,小文步行一段时间后,小亮骑自行车沿相同路线行进,两人均匀速前行.他们的路程差 (单位:米)与小文出发时间 (单位:分)之间的函数关系如图所示.下列说法:① 小亮先到达青少年宫;② 小亮的速度是小文速度的 倍;③ ;④ .其中正确的是
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
二、填空题(共2小题;共10分)
7. 已知点 , 都在函数 的图象上,则 .
8. 小明放学后步行回家,他离家的路程 (单位:米)与步行时间 (单位:分)的函数图象如图所示,则他步行回家的平均速度是 .
三、解答题(共4小题;共52分)
9. 如图为一位旅行者在早晨 时从城市出发到郊外所走的路程 (单位:千米)与时间 (单位:时)的变量关系的图象.根据图象回答问题:
(1)在这个变化过程中,自变量是 ,函数是 ;
(2) 时, 时所走的路程分别是多少
(3)他休息了多长时间
(4)他从休息后直至到达目的地这段时间的平均速度是多少
10. 画出函数 的图象,并判断点 ,,, 在不在函数图象上.
11. 图① 中的摩天轮可抽象成一个圆,圆上一点离地面的高度 与旋转时间 之间的关系如图② 所示.
(1)根据图② 填表:
(2)变量 是 的函数吗 为什么
(3)根据图中的信息,请写出摩天轮的直径.
12. (1)画出函数 的图象;
(2)试判断点 是否在上述函数图象上.
答案
第一部分
1. C
2. A
3. D
4. B
5. C
6. B 【解析】根据图象知,小文步行 分钟时,小亮开始出发, 分钟时两人相遇,之后小亮超过小文,在 分钟时,小亮到达目的地, 分钟时,小文到达目的地.
小文的速度 (米 /秒),小亮的速度 (米 /秒) .
(米);
(秒).
第二部分
7.
8.
第三部分
9. (1) 时间 ;路程 .
(2) 时, 时所走的路程分别是 千米, 千米.
(3) 该旅行者休息的时间为 小时.
(4) 他从休息后直至到达目的地这段时间的平均速度是 .
10. 函数图象如图:
点 , 在函数 的图象上,点 , 不在函数 的图象上.
11. (1)
(2) 是 的函数.由图象可知,变量 随着 的变化而变化,同时对于每一个 ,按照图象,都有唯一的变量 与之相对应,符合函数的定义.
(3) 摩天轮的直径是 .
12. (1)
(2) 点 不在函数 的图象上.
第1页(共1 页)
