人教版八年级下册 19.2.2 一次函数-第2课时 一次函数的图象与性质 同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册 19.2.2 一次函数-第2课时 一次函数的图象与性质 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 243.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-15 17:15:11 | ||
图片预览

文档简介
八下-第十九章 一次函数-19.2 一次函数-19.2.2 一次函数-第2课时 一次函数的图象与性质
一、选择题(共9小题;共45分)
1. 一次函数 的大致图象是
A. B.
C. D.
2. 一次函数 的图象与 轴交点的坐标是
A. B. C. D.
3. 将函数 的图象沿 轴向上平移 个单位长度后,所得图象对应的函数解析式为
A. B.
C. D.
4. 一次函数 的图象不经过
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5. 若点 在一次函数 的图象上,则 的值是
A. B. C. D.
6. 下列函数中, 随 的增大而减小的函数是
A. B. C. D.
7. 已知点 和点 是一次函数 的图象上的两点,则 与 的大小关系是
A. B. C. D. 以上都不对
8. 若式子 有意义,则一次函数 的图象可能是
A. B.
C. D.
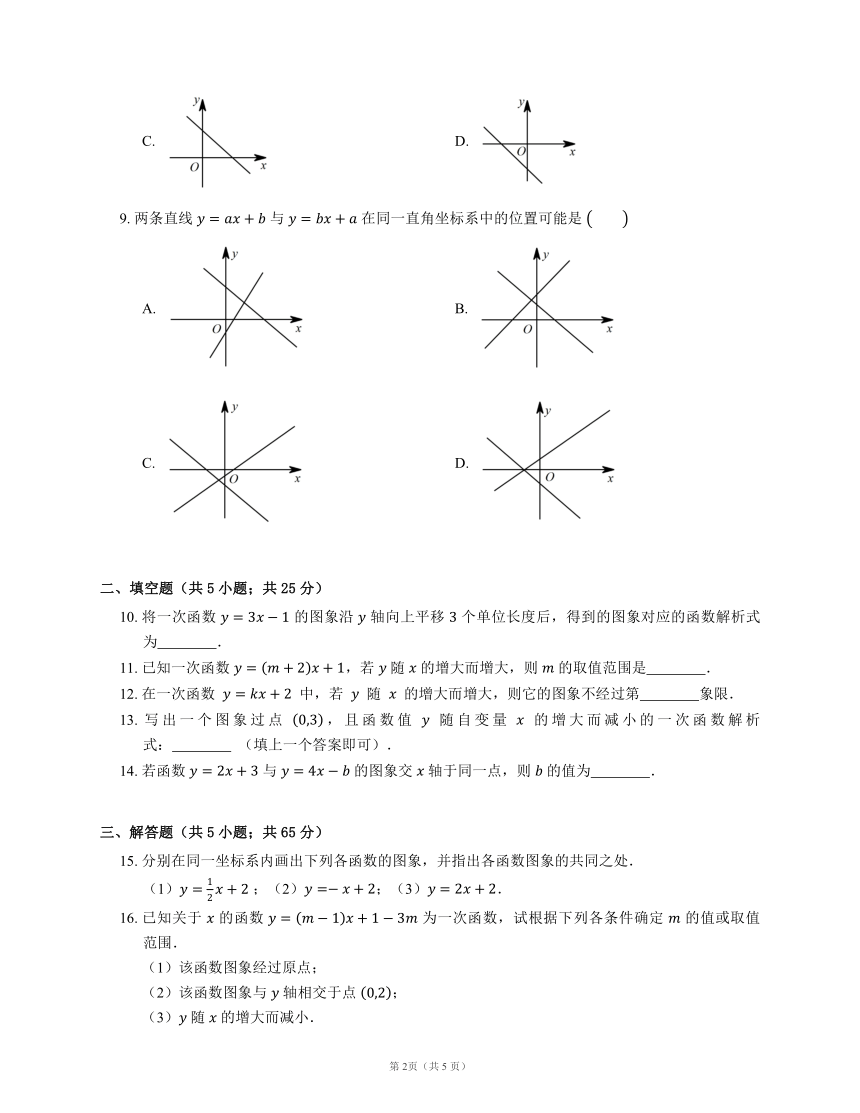
9. 两条直线 与 在同一直角坐标系中的位置可能是
A. B.
C. D.
二、填空题(共5小题;共25分)
10. 将一次函数 的图象沿 轴向上平移 个单位长度后,得到的图象对应的函数解析式为 .
11. 已知一次函数 ,若 随 的增大而增大,则 的取值范围是 .
12. 在一次函数 中,若 随 的增大而增大,则它的图象不经过第 象限.
13. 写出一个图象过点 ,且函数值 随自变量 的增大而减小的一次函数解析式: (填上一个答案即可).
14. 若函数 与 的图象交 轴于同一点,则 的值为 .
三、解答题(共5小题;共65分)
15. 分别在同一坐标系内画出下列各函数的图象,并指出各函数图象的共同之处.
(1) ;(2);(3).
16. 已知关于 的函数 为一次函数,试根据下列各条件确定 的值或取值范围.
(1)该函数图象经过原点;
(2)该函数图象与 轴相交于点 ;
(3) 随 的增大而减小.
17. 已知直线 与 轴相交于点 ,与 轴相交于点 ,求这条直线与坐标轴围成的三角形的面积.
18. 已知直线 .
(1) 为何值时,该直线经过第二、三、四象限
(2) 为何值时,该直线与直线 平行
19. 元旦联欢会前某班布置教室,同学们利用彩条粘成一环套一环的彩纸链,小颖测量了部分彩纸链的长度,她得到纸环数 (个)与彩纸链长度 的数据如下表:
(1)把上表中 , 的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出相应的点,猜想 关于 的函数解析式;
(2)若教室天花板的对角线的长为 ,现需沿天花板两条对角线各拉一根彩纸链,则每根彩纸链至少要用多少个纸环
答案
第一部分
1. A 【解析】 ,
.
一次函数 的图象经过第一、二、四象限.
2. B
3. A
4. C
5. D
6. C
7. A
8. A 【解析】要使式子 有意义,则 且 ,
,
,
一次函数 的图象经过第一、三、四象限.
9. A
第二部分
10.
11.
12. 四
13. 答案不唯一,如
14.
第三部分
15. 如图:
由图可知:这三个函数的图象都经过同一个点 .
16. (1) .
(2) .
(3) .
17. 直线 与 轴相交于点 ,与 轴相交于点 ,
, .
, .
这条直线与坐标轴围成的三角形的面积 .
18. (1) 直线经过第二、三、四象限,
.
(2) 与直线 平行,
.
.
19. (1) 如图,
( 为正整数).
(2) 由 .
.
.
答:每根彩纸链至少要用 个纸环.
第1页(共1 页)
一、选择题(共9小题;共45分)
1. 一次函数 的大致图象是
A. B.
C. D.
2. 一次函数 的图象与 轴交点的坐标是
A. B. C. D.
3. 将函数 的图象沿 轴向上平移 个单位长度后,所得图象对应的函数解析式为
A. B.
C. D.
4. 一次函数 的图象不经过
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5. 若点 在一次函数 的图象上,则 的值是
A. B. C. D.
6. 下列函数中, 随 的增大而减小的函数是
A. B. C. D.
7. 已知点 和点 是一次函数 的图象上的两点,则 与 的大小关系是
A. B. C. D. 以上都不对
8. 若式子 有意义,则一次函数 的图象可能是
A. B.
C. D.
9. 两条直线 与 在同一直角坐标系中的位置可能是
A. B.
C. D.
二、填空题(共5小题;共25分)
10. 将一次函数 的图象沿 轴向上平移 个单位长度后,得到的图象对应的函数解析式为 .
11. 已知一次函数 ,若 随 的增大而增大,则 的取值范围是 .
12. 在一次函数 中,若 随 的增大而增大,则它的图象不经过第 象限.
13. 写出一个图象过点 ,且函数值 随自变量 的增大而减小的一次函数解析式: (填上一个答案即可).
14. 若函数 与 的图象交 轴于同一点,则 的值为 .
三、解答题(共5小题;共65分)
15. 分别在同一坐标系内画出下列各函数的图象,并指出各函数图象的共同之处.
(1) ;(2);(3).
16. 已知关于 的函数 为一次函数,试根据下列各条件确定 的值或取值范围.
(1)该函数图象经过原点;
(2)该函数图象与 轴相交于点 ;
(3) 随 的增大而减小.
17. 已知直线 与 轴相交于点 ,与 轴相交于点 ,求这条直线与坐标轴围成的三角形的面积.
18. 已知直线 .
(1) 为何值时,该直线经过第二、三、四象限
(2) 为何值时,该直线与直线 平行
19. 元旦联欢会前某班布置教室,同学们利用彩条粘成一环套一环的彩纸链,小颖测量了部分彩纸链的长度,她得到纸环数 (个)与彩纸链长度 的数据如下表:
(1)把上表中 , 的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出相应的点,猜想 关于 的函数解析式;
(2)若教室天花板的对角线的长为 ,现需沿天花板两条对角线各拉一根彩纸链,则每根彩纸链至少要用多少个纸环
答案
第一部分
1. A 【解析】 ,
.
一次函数 的图象经过第一、二、四象限.
2. B
3. A
4. C
5. D
6. C
7. A
8. A 【解析】要使式子 有意义,则 且 ,
,
,
一次函数 的图象经过第一、三、四象限.
9. A
第二部分
10.
11.
12. 四
13. 答案不唯一,如
14.
第三部分
15. 如图:
由图可知:这三个函数的图象都经过同一个点 .
16. (1) .
(2) .
(3) .
17. 直线 与 轴相交于点 ,与 轴相交于点 ,
, .
, .
这条直线与坐标轴围成的三角形的面积 .
18. (1) 直线经过第二、三、四象限,
.
(2) 与直线 平行,
.
.
19. (1) 如图,
( 为正整数).
(2) 由 .
.
.
答:每根彩纸链至少要用 个纸环.
第1页(共1 页)
