人教版八年级下册19.2.2 一次函数-第3课时 一次函数解析式的求法 同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册19.2.2 一次函数-第3课时 一次函数解析式的求法 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 110.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-15 17:15:29 | ||
图片预览


文档简介
八下-第十九章 一次函数-19.2 一次函数-19.2.2 一次函数-第3课时 一次函数解析式的求法
一、选择题(共6小题;共30分)
1. 一名老师带领 名学生到动物园参观,已知成人票每张 元,学生票每张 元,设门票的总费用为 元,则 与 的函数解析式为
A. B. C. D.
2. 根据下表中一次函数的自变量 与函数 的对应值,可得 的值为
A. B. C. D.
3. 一次函数 的图象如图所示,则下列结论正确的是
A. B. C. D.
4. 已知一次函数 ,当 时,,且它的图象与 轴交点的纵坐标是 ,那么该函数的解析式为
A. B. C. D.
5. 如图,过点 的一次函数的图象与正比例函数 的图象相交于点 ,则这个一次函数的解析式是
A. B. C. D.
6. 在直角坐标系中,一直线 向下平移 个单位后所得直线 经过点 ,将直线 绕点 顺时针旋转 后所得直线经过点 ,则直线 的函数关系式为
A. B. C. D.
二、填空题(共6小题;共30分)
7. 若一次函数 ( 为常数)的图象经过点 ,则 的值为 .
8. 把直线 沿 轴向右平移 个单位长度,所得直线的函数解析式为 .
9. 在平面直角坐标中,已知点 ,,直线 与线段 有交点,则 的取值范围为 .
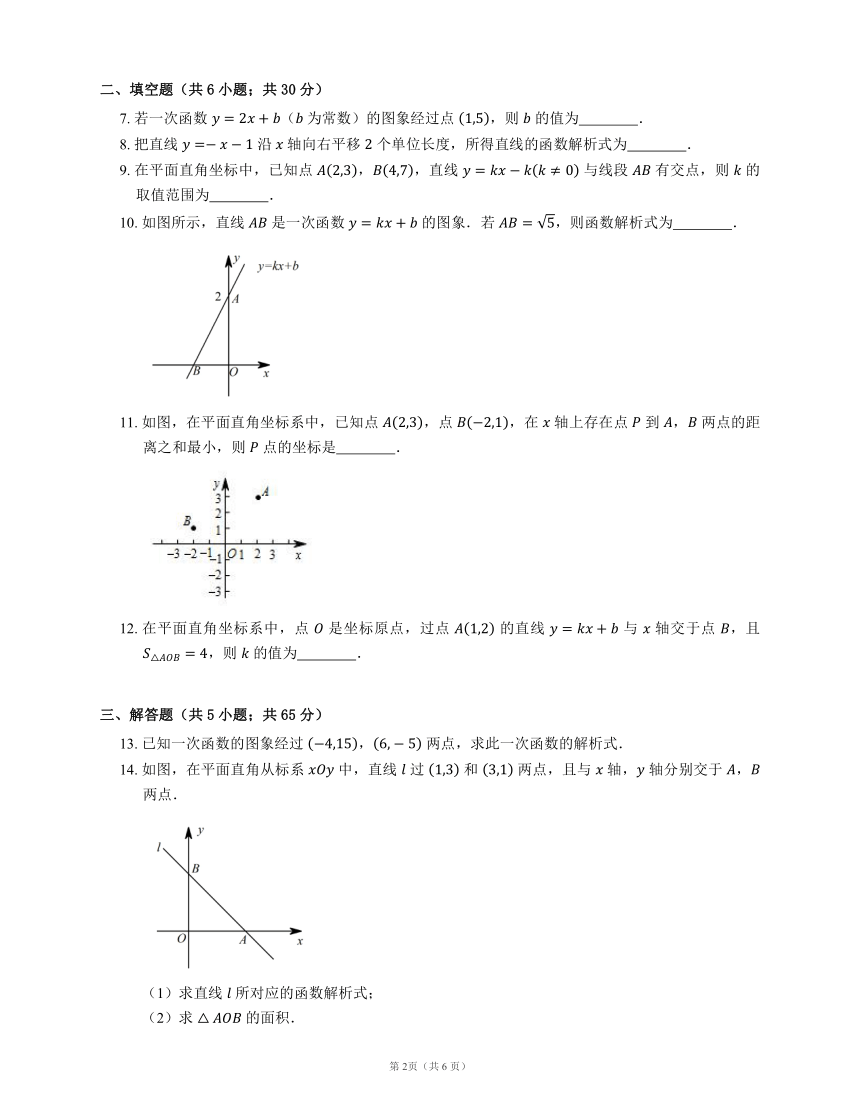
10. 如图所示,直线 是一次函数 的图象.若 ,则函数解析式为 .
11. 如图,在平面直角坐标系中,已知点 ,点 ,在 轴上存在点 到 , 两点的距离之和最小,则 点的坐标是 .
12. 在平面直角坐标系中,点 是坐标原点,过点 的直线 与 轴交于点 ,且 ,则 的值为 .
三、解答题(共5小题;共65分)
13. 已知一次函数的图象经过 , 两点,求此一次函数的解析式.
14. 如图,在平面直角从标系 中,直线 过 和 两点,且与 轴, 轴分别交于 , 两点.
(1)求直线 所对应的函数解析式;
(2)求 的面积.
15. 鞋子的“鞋码”和鞋长 存在着一次函数关系,下表是几组“鞋码”与鞋长换算的对应数值.[注:“鞋码”是表示鞋子大小的一种号码]
(1)设鞋长为 ,“鞋码”为 ,求 与 之间的函数解析式;
(2)如果某人穿 号鞋,那么他的鞋长是多少
16. 一次函数 的图象过点 ,并且与 轴相交于点 ,直线 与 轴相交于点 ,点 与点 关于 轴对称,求这个一次函数的解析式.
17. 如图,已知一条直线经过点 ,,将这条直线向左平移与 轴, 轴分别交于点 ,.若 ,求直线 所对应的函数解析式.
答案
第一部分
1. A
2. A 【解析】设 ,将表格中对应的 , 的值代入得二元一次方程组,解方程组得 , 的值,回代 时,得到对应的 值即可.
设 , 解得 ,.
,当 时,得 .
3. D
4. C
5. D
6. C 【解析】设直线 的解析式为 ,
,,
代入得
解得
直线 的解析式为 .
由题意,知直线 绕点 逆时针旋转 后得到直线 ,
则直线 经过 ,,
易求直线 的解析式为 ,
将直线 向上平移 个单位后得直线 ,
所以直线 的解析式为 ,即 .
第二部分
7.
8.
9.
【解析】直线 过定点 .
当直线过点 时,;
当直线过点 时,.
的取值范围是 .
10.
【解析】提示:由勾股定理,得 , .
11.
【解析】,
则点 关于 轴对称点的坐标为 .
连接 与 轴交于点 ,
则 点到 , 两点间的距离之和最小.
设直线 的解析式为 .
,,
解得
直线 的解析式为 .
当 时,.
点 的坐标为 .
12. 或
【解析】把 代入 ,得 ,解得 .
所以 点坐标为 .
把 代入 ,得 ,则 ,
,
.
.
解得 或
第三部分
13. 设一次函数解析式为 .
直线 过 , 两点,
解得
所以一次函数的解析式为 .
14. (1) 设直线 所对应的函数解析式 .
直线 过 , 两点,
解得
所以直线 所对应的函数解析式为 .
(2) 当 时,;当 时,;
, .
.
15. (1) 设一次函数函数解析式为 .
时,; 时,;
解得
关于 的函数解析式为 .( 是一些不连续的值,一般情况下, 取 ,,,,,,, 等)
(2) 当 时,,
解得 .
答:他的鞋长为 .
16. 直线 与 轴的交点为 ,
.
点 与点 关于 轴对称,
.
一次函数 的图象与 轴交于点 ,
.
一次函数为 .
一次函数 的图象过点 ,
.
解得 .
这个函数解析式为 .
17. 设直线 的解析式为 .
直线经过点 ,,
解得
直线 的解析式为 .
为直线 向左平移得到,
设直线 的解析式为 ,
, ,
.
点 .
.
解得 .
直线 的解析式为 .
第1页(共1 页)
一、选择题(共6小题;共30分)
1. 一名老师带领 名学生到动物园参观,已知成人票每张 元,学生票每张 元,设门票的总费用为 元,则 与 的函数解析式为
A. B. C. D.
2. 根据下表中一次函数的自变量 与函数 的对应值,可得 的值为
A. B. C. D.
3. 一次函数 的图象如图所示,则下列结论正确的是
A. B. C. D.
4. 已知一次函数 ,当 时,,且它的图象与 轴交点的纵坐标是 ,那么该函数的解析式为
A. B. C. D.
5. 如图,过点 的一次函数的图象与正比例函数 的图象相交于点 ,则这个一次函数的解析式是
A. B. C. D.
6. 在直角坐标系中,一直线 向下平移 个单位后所得直线 经过点 ,将直线 绕点 顺时针旋转 后所得直线经过点 ,则直线 的函数关系式为
A. B. C. D.
二、填空题(共6小题;共30分)
7. 若一次函数 ( 为常数)的图象经过点 ,则 的值为 .
8. 把直线 沿 轴向右平移 个单位长度,所得直线的函数解析式为 .
9. 在平面直角坐标中,已知点 ,,直线 与线段 有交点,则 的取值范围为 .
10. 如图所示,直线 是一次函数 的图象.若 ,则函数解析式为 .
11. 如图,在平面直角坐标系中,已知点 ,点 ,在 轴上存在点 到 , 两点的距离之和最小,则 点的坐标是 .
12. 在平面直角坐标系中,点 是坐标原点,过点 的直线 与 轴交于点 ,且 ,则 的值为 .
三、解答题(共5小题;共65分)
13. 已知一次函数的图象经过 , 两点,求此一次函数的解析式.
14. 如图,在平面直角从标系 中,直线 过 和 两点,且与 轴, 轴分别交于 , 两点.
(1)求直线 所对应的函数解析式;
(2)求 的面积.
15. 鞋子的“鞋码”和鞋长 存在着一次函数关系,下表是几组“鞋码”与鞋长换算的对应数值.[注:“鞋码”是表示鞋子大小的一种号码]
(1)设鞋长为 ,“鞋码”为 ,求 与 之间的函数解析式;
(2)如果某人穿 号鞋,那么他的鞋长是多少
16. 一次函数 的图象过点 ,并且与 轴相交于点 ,直线 与 轴相交于点 ,点 与点 关于 轴对称,求这个一次函数的解析式.
17. 如图,已知一条直线经过点 ,,将这条直线向左平移与 轴, 轴分别交于点 ,.若 ,求直线 所对应的函数解析式.
答案
第一部分
1. A
2. A 【解析】设 ,将表格中对应的 , 的值代入得二元一次方程组,解方程组得 , 的值,回代 时,得到对应的 值即可.
设 , 解得 ,.
,当 时,得 .
3. D
4. C
5. D
6. C 【解析】设直线 的解析式为 ,
,,
代入得
解得
直线 的解析式为 .
由题意,知直线 绕点 逆时针旋转 后得到直线 ,
则直线 经过 ,,
易求直线 的解析式为 ,
将直线 向上平移 个单位后得直线 ,
所以直线 的解析式为 ,即 .
第二部分
7.
8.
9.
【解析】直线 过定点 .
当直线过点 时,;
当直线过点 时,.
的取值范围是 .
10.
【解析】提示:由勾股定理,得 , .
11.
【解析】,
则点 关于 轴对称点的坐标为 .
连接 与 轴交于点 ,
则 点到 , 两点间的距离之和最小.
设直线 的解析式为 .
,,
解得
直线 的解析式为 .
当 时,.
点 的坐标为 .
12. 或
【解析】把 代入 ,得 ,解得 .
所以 点坐标为 .
把 代入 ,得 ,则 ,
,
.
.
解得 或
第三部分
13. 设一次函数解析式为 .
直线 过 , 两点,
解得
所以一次函数的解析式为 .
14. (1) 设直线 所对应的函数解析式 .
直线 过 , 两点,
解得
所以直线 所对应的函数解析式为 .
(2) 当 时,;当 时,;
, .
.
15. (1) 设一次函数函数解析式为 .
时,; 时,;
解得
关于 的函数解析式为 .( 是一些不连续的值,一般情况下, 取 ,,,,,,, 等)
(2) 当 时,,
解得 .
答:他的鞋长为 .
16. 直线 与 轴的交点为 ,
.
点 与点 关于 轴对称,
.
一次函数 的图象与 轴交于点 ,
.
一次函数为 .
一次函数 的图象过点 ,
.
解得 .
这个函数解析式为 .
17. 设直线 的解析式为 .
直线经过点 ,,
解得
直线 的解析式为 .
为直线 向左平移得到,
设直线 的解析式为 ,
, ,
.
点 .
.
解得 .
直线 的解析式为 .
第1页(共1 页)
