2021-2022学年山东省济南市莱芜实验中学片区教研共同体九年级(上)期中数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2021-2022学年山东省济南市莱芜实验中学片区教研共同体九年级(上)期中数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 537.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 12:42:40 | ||
图片预览



文档简介
2021-2022学年山东省济南市莱芜实验中学片区教研共同体九年级(上)期中数学试卷(五四学制)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.(3分)若函数y=(k≠0)的图象过点(1,),则此函数图象位于( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
2.(3分)已知反比例函数y=﹣,下列结论不正确的是( )
A.图象必经过点(﹣1,2) B.若x>1,则y>﹣2
C.图象在第二、四象限内 D.y随x的增大而增大
3.(3分)对于二次函数y=(x+1)2+2的图象,下列说法正确的是( )
A.开口向下 B.对称轴是直线x=﹣1
C.顶点坐标是(1,2) D.与x轴有两个交点
4.(3分)如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )
A. B. C. D.
5.(3分)若抛物线是关于x的二次函数,那么m的值是( )
A.3 B.﹣2 C.2 D.2或3
6.(3分)在Rt△ACB中,∠C=90°,,则sinB的值为( )
A. B. C. D.
7.(3分)若代数式有意义,则实数x的取值范围是( )
A.x≥﹣1 B.x≥﹣1且x≠3 C.x>﹣1 D.x>﹣1且x≠3
8.(3分)已知点A(﹣3,y1),B(2,y2),C(3,y3)在抛物线y=2x2﹣4x+c上,则y1、y2、y3的大小关系是( )
A.y1>y2>y3 B.y1>y3>y2 C.y3>y2>y1 D.y2>y3>y1
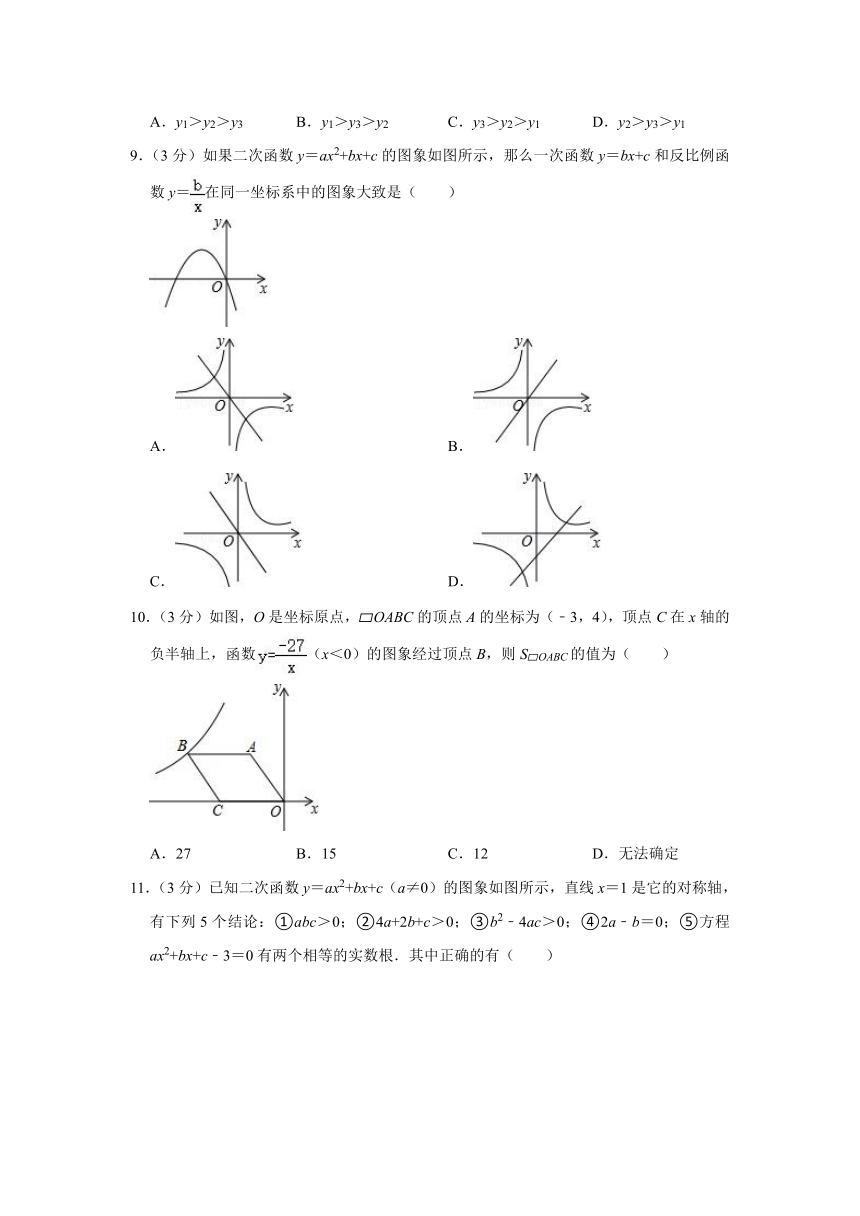
9.(3分)如果二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=在同一坐标系中的图象大致是( )
A. B.
C. D.
10.(3分)如图,O是坐标原点, OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数(x<0)的图象经过顶点B,则S OABC的值为( )
A.27 B.15 C.12 D.无法确定
11.(3分)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,直线x=1是它的对称轴,有下列5个结论:①abc>0;②4a+2b+c>0;③b2﹣4ac>0;④2a﹣b=0;⑤方程ax2+bx+c﹣3=0有两个相等的实数根.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
12.(3分)如图,点A、C在反比例函数y=的图象上,点B、D在反比例函数y=的图象上,a>b>0,AB∥CD∥x轴,AB、CD在x轴的两侧,AB=,CD=,AB、CD的距离为6,则a﹣b的值为( )
A.3 B. C.﹣3 D.无法确定
二、填空题
13.(3分)如图抛物线y=ax2与反比例函数交于点C(1,2),则不等式的解集是 .
14.(3分)△ABC中,∠A、∠B都是锐角,若sinA=,cosB=,则∠C= .
15.(3分)若函数y=(1﹣m)+2是关于x的二次函数,且抛物线的开口向上,则m的值为 .
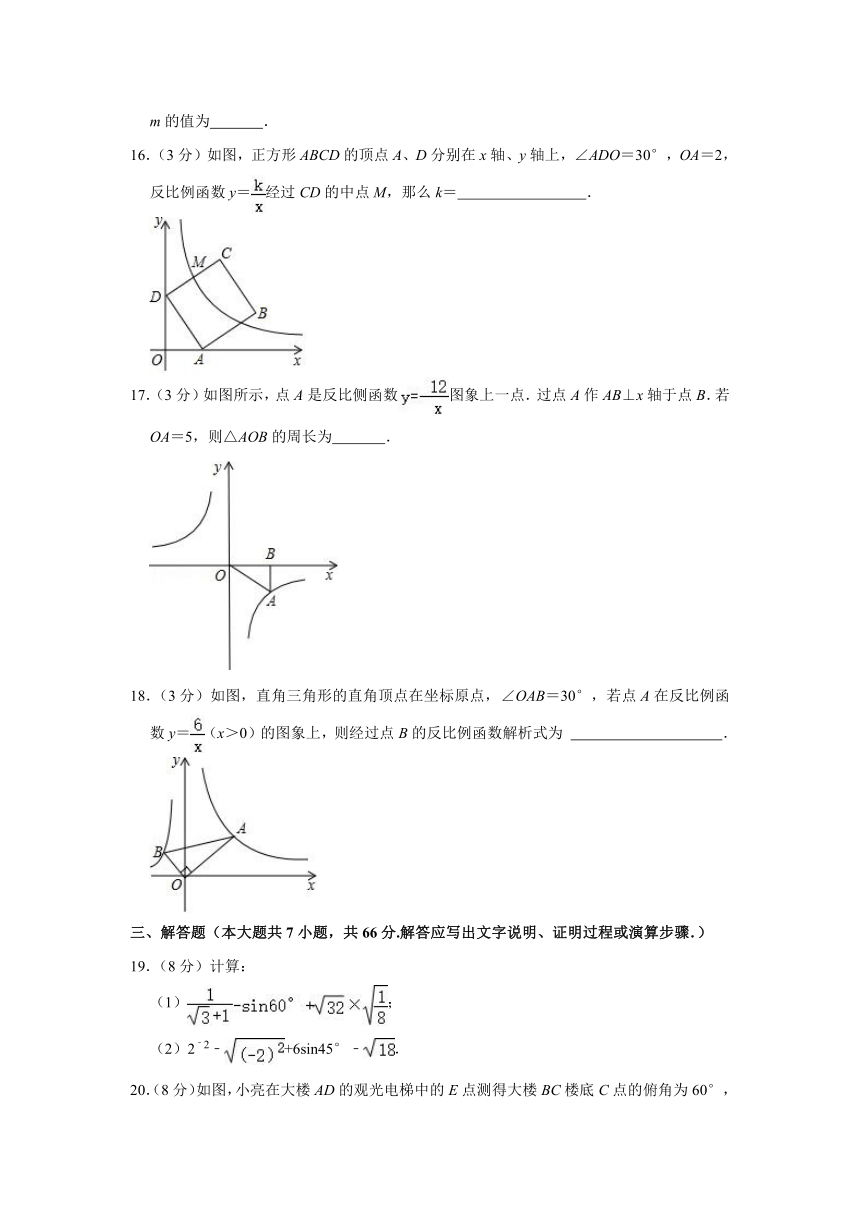
16.(3分)如图,正方形ABCD的顶点A、D分别在x轴、y轴上,∠ADO=30°,OA=2,反比例函数y=经过CD的中点M,那么k= .
17.(3分)如图所示,点A是反比侧函数图象上一点.过点A作AB⊥x轴于点B.若OA=5,则△AOB的周长为 .
18.(3分)如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=(x>0)的图象上,则经过点B的反比例函数解析式为 .
三、解答题(本大题共7小题,共66分.解答应写出文字说明、证明过程或演算步骤.)
19.(8分)计算:
(1);
(2)2﹣2﹣+6sin45°﹣.
20.(8分)如图,小亮在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为60°,此时他距地面的高度AE为21米,电梯再上升9米到达D点,此时测得大楼BC楼顶B点的仰角为45°,求大楼BC的高度.(结果保留根号)
21.(8分)如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
(1)求改造前坡顶与地面的距离BE的长;
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
【参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75】
22.(10分)在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
23.(10分)“佳佳商场”在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,“佳佳商场”应将这种商品的售价定为多少?
(2)物价局规定该商品的售价不能超过40元/件,“佳佳商场”为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
24.(10分)如图,一次函数y1=ax+b与反比例函数y2=的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围为 ;
(3)点P是x轴上一点,当S△PAC=S△AOB时,请直接写出点P的坐标为 .
25.(12分)如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为2?若存在求出点Q的坐标;若不存在请说明理由.
2021-2022学年山东省济南市莱芜实验中学片区教研共同体九年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.(3分)若函数y=(k≠0)的图象过点(1,),则此函数图象位于( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
【分析】先由已知点求出k的值,然后得到函数图象所在的象限.
【解答】解:∵函数y=(k≠0)的图象过点(1,),
∴k=1×=>0,
∴函数图象位于第一、三象限.
故选:B.
2.(3分)已知反比例函数y=﹣,下列结论不正确的是( )
A.图象必经过点(﹣1,2) B.若x>1,则y>﹣2
C.图象在第二、四象限内 D.y随x的增大而增大
【分析】根据反比例函数的性质:当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大进行分析即可.
【解答】解:A、图象必经过点(﹣1,2),说法正确,不合题意;
B、若x>1,则﹣2<y<0,说法错误,符合题意;
C、k=﹣2<0,图象在第二、四象限内,说法正确,不合题意;
D、k=﹣2<0,每个象限内,y随x的增大而增大,说法正确,不合题意;
故选:B.
3.(3分)对于二次函数y=(x+1)2+2的图象,下列说法正确的是( )
A.开口向下 B.对称轴是直线x=﹣1
C.顶点坐标是(1,2) D.与x轴有两个交点
【分析】根据a的正负判断开口方向,通过抛物线的y=a(x﹣h)2+k解析式判定对称轴、顶点坐标,根据顶点坐标和开口方向即可判断抛物线与x轴交点个数.
【解答】解:∵抛物线a>0,所以开口向上,A选项错误;顶点坐标为(﹣1,2),所以C选项错误;
根据顶点坐标以及开口向上可判定与x轴没有交点,
∴D选项错误;
对称轴为直线x=﹣1,B选项正确.
故选:B.
4.(3分)如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )
A. B. C. D.
【分析】直接连接DC,得出CD⊥AB,再结合勾股定理以及锐角三角函数关系得出答案
【解答】解:连接DC,
由网格可得:CD⊥AB,
则DC=,AC=,
故sinA=.
故选:D.
5.(3分)若抛物线是关于x的二次函数,那么m的值是( )
A.3 B.﹣2 C.2 D.2或3
【分析】根据二次函数的最高指数是2,二次项系数不等于0列出方程求解即可.
【解答】解:由题意得,m2﹣5m+8=2且m﹣3≠0,
解得m1=2,m2=3,且m≠3,
所以,m=2.
故选:C.
6.(3分)在Rt△ACB中,∠C=90°,,则sinB的值为( )
A. B. C. D.
【分析】根据锐角三角函数的定义进行计算即可.
【解答】解:设Rt△ACB中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,
由于tanA==2,
可设a=2k,b=k,由勾股定理得,
c==5k,
∴sinB==,
故选:A.
7.(3分)若代数式有意义,则实数x的取值范围是( )
A.x≥﹣1 B.x≥﹣1且x≠3 C.x>﹣1 D.x>﹣1且x≠3
【分析】根据被开方数大于等于0,分母不等于0列式计算即可得解.
【解答】解:由题意得,x+1≥0且x﹣3≠0,
解得:x≥﹣1且x≠3.
故选:B.
8.(3分)已知点A(﹣3,y1),B(2,y2),C(3,y3)在抛物线y=2x2﹣4x+c上,则y1、y2、y3的大小关系是( )
A.y1>y2>y3 B.y1>y3>y2 C.y3>y2>y1 D.y2>y3>y1
【分析】先配方得到抛物线的对称轴为直线x=1,根据二次函数的性质,通过三点与对称轴距离的远近来比较函数值的大小.
【解答】解:y=2x2﹣4x+c=2(x﹣1)2+c﹣2,
则抛物线的对称轴为直线x=1,
∵抛物线开口向上,点A(﹣3,y1)到对称轴的距离最远,点B(2,y2)到对称轴的距离最近,
∴y1>y3>y2.
故选:B.
9.(3分)如果二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=在同一坐标系中的图象大致是( )
A. B.
C. D.
【分析】根据二次函数的图象的性质先确定出a、b、c的取值范围,然后根据一次函数和反比例函数的性质即可做出判断.
【解答】解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴由于y轴的左侧;
∴a与b同号,
∴b<0,
∵抛物线经过原点,所以c=0.
∵b<0,c=0,
∴直线y=bx+c经过二、四象限和坐标原点.
∵b<0,
∴反比例函数的图象,位于二、四象限.
故选:A.
10.(3分)如图,O是坐标原点, OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数(x<0)的图象经过顶点B,则S OABC的值为( )
A.27 B.15 C.12 D.无法确定
【分析】过点A作AD⊥y轴于点D,过点B作BE⊥x轴于点E,根据反比例函数系数k的几何意义得S矩形BDOE=27,进而求得BD,进一步得到AB,根据矩形面积公式即可求得答案.
【解答】解:过点A作AD⊥y轴于点D,过点B作BE⊥x轴于点E,
∵函数(x<0)的图象经过顶点B,
∴S矩形BDOE=27,
∵ OABC的顶点A的坐标为(﹣3,4),
∴AD=3,DO=4,
∴BD OA=27,即BD×4=27,
∴BD=,
∴OC=AB=﹣3=,
∴S OABC=OC OD=15,
故选:B.
11.(3分)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,直线x=1是它的对称轴,有下列5个结论:①abc>0;②4a+2b+c>0;③b2﹣4ac>0;④2a﹣b=0;⑤方程ax2+bx+c﹣3=0有两个相等的实数根.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据二次函数的图象与性质即可求出答案.
【解答】解:①由图象可知:a<0,c>0,
>0,
∴b>0,
∴abc<0,故①错误;
②抛物线的对称轴为x=1,
∴(﹣1,y)关于直线x=1的对称点为(3,y),
(0,c)关于直线x=1的对称点为(2,c)
∴x=2,y=4a+2b+c>0,故②正确;
③抛物线与x轴有两个交点,
∴Δ=b2﹣4ac>0,故③正确;
④由对称轴可知:=1,
∴2a+b=0,故④错误;
⑤由图象可知:y=3时,
此时ax2+bx+c=3只有一解x=1,
∴方程ax2+bx+c﹣3=0有两个相同的根,故⑤正确;
故选:C.
12.(3分)如图,点A、C在反比例函数y=的图象上,点B、D在反比例函数y=的图象上,a>b>0,AB∥CD∥x轴,AB、CD在x轴的两侧,AB=,CD=,AB、CD的距离为6,则a﹣b的值为( )
A.3 B. C.﹣3 D.无法确定
【分析】设点A、B的纵坐标为y1,点C、D的纵坐标为y2,分别表示出来A、B、C、D四点的坐标,根据线段AB、CD的长度结合AB与CD间的距离,即可得出y1、y2的值,再由点A、B的横坐标结合AB=即可求出a﹣b的值.
【解答】解:设点A、B的纵坐标为y1(y1>0),点C、D的纵坐标为y2(y2<0),则点A(,y1),点B(,y1),
∵AB=,CD=,
∴2×||=||,
∴|y1|=2|y2|.
∵|y1|+|y2|=6,
∴y1=4,y2=﹣2.
∴AB=﹣==,
∴a﹣b=3.
故选:A.
二、填空题
13.(3分)如图抛物线y=ax2与反比例函数交于点C(1,2),则不等式的解集是 x<0或x>1 .
【分析】结合函数图象即可得出解集.
【解答】解:由图可知,当x<0或x>1时抛物线y=ax2在反比例函数图象的上方,
当0<x<1时,抛物线y=ax2在反比例函数图象的下方,
∴不等式的解集是x<0或x>1.
故答案为:x<0或x>1.
14.(3分)△ABC中,∠A、∠B都是锐角,若sinA=,cosB=,则∠C= 60° .
【分析】先根据特殊角的三角函数值求出∠A、∠B的度数,再根据三角形内角和定理求出∠C即可作出判断.
【解答】解:∵△ABC中,∠A、∠B都是锐角sinA=,cosB=,
∴∠A=∠B=60°.
∴∠C=180°﹣∠A﹣∠B=180°﹣60°﹣60°=60°.
故答案为:60°.
15.(3分)若函数y=(1﹣m)+2是关于x的二次函数,且抛物线的开口向上,则m的值为 ﹣2 .
【分析】先依据二次函数的定义知,系数1﹣m一定不为0,1﹣m>0,再得出m2﹣2=2,求出m的值即可.
【解答】解:由题意得:1﹣m≠0,
解得:m≠1,
∵抛物线的开口向上,
∴1﹣m>0,
解得:m<1,
∵m2﹣2=2,
∴解得:m=±2,
∴m=﹣2.
故答案为:﹣2.
16.(3分)如图,正方形ABCD的顶点A、D分别在x轴、y轴上,∠ADO=30°,OA=2,反比例函数y=经过CD的中点M,那么k= +6 .
【分析】作CE⊥y轴于点E,先证明△CDE≌△DAO,得到DE=AO=2,DO=2=CE,再根据M是CD的中点,即可得到M(,1+2),最后根据反比例函数y=经过CD的中点M,即可得到k的值.
【解答】解:如图,作CE⊥y轴于点E.
∵正方形ABCD的顶点A、D分别在x轴、y轴上,
∴∠CED=∠DOA=90°,∠DCE=∠ADO,CD=DA,
∴△CDE≌△DAO(AAS),
∴DE=AO=2,
又∵∠ODA=30°,
∴Rt△AOD中,AD=2AO=4,DO=2=CE,
∴EO=2+2,
∴C(2,2+2),D(0,2),
∵M是CD的中点,
∴M(,1+2),
∵反比例函数y=经过CD的中点M,
∴k=(1+2)=+6,
故答案为:+6.
17.(3分)如图所示,点A是反比侧函数图象上一点.过点A作AB⊥x轴于点B.若OA=5,则△AOB的周长为 12 .
【分析】设A的坐标是(a,﹣b),则ab=12,在直角△AOB中利用勾股定理即可求得a2+b2的值,利用完全平方式即可求得a+b的值,即直角三角形的两直角边的长,则周长即可求得.
【解答】解:设A的坐标是(a,﹣b),则ab=12,
∵OA=5,
∴a2+b2=25,
∴(a+b)2=a2+b2+2ab=25+24=49,
∵a+b>0,
∴a+b=7,
故△AOB的周长是:7+5=12.
故答案是:12.
18.(3分)如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=(x>0)的图象上,则经过点B的反比例函数解析式为 y=﹣ .
【分析】过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D,证明△BCO∽△ODA,利用相似三角形的判定与性质得出=,根据反比例函数图象上点的坐标特征得出S△AOD=3,那么S△BCO=1,进而得出答案.
【解答】解:过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D,如图.
∵∠BOA=90°,
∴∠BOC+∠AOD=90°,
∵∠AOD+∠OAD=90°,
∴∠BOC=∠OAD,
又∵∠BCO=∠ADO=90°,
∴△BCO∽△ODA,
∴=tan30°=,
∴=,
∵×AD×DO=xy=3,
∴S△BCO=×BC×CO=S△AOD=1,
∵经过点B的反比例函数图象在第二象限,
故反比例函数解析式为:y=﹣.
故答案为y=﹣.
三、解答题(本大题共7小题,共66分.解答应写出文字说明、证明过程或演算步骤.)
19.(8分)计算:
(1);
(2)2﹣2﹣+6sin45°﹣.
【分析】(1)先分母有理化、代入三角函数、计算二次根式的乘法,再计算加减即可;
(2)先计算负整数指数幂、代入三角函数值、利用二次根式的性质化简,再计算乘法,最后计算加减即可.
【解答】解:(1)原式=﹣+
=﹣+2
=﹣+2
=;
(2)原式=﹣2+6×﹣3
=﹣2+3﹣3
=﹣.
20.(8分)如图,小亮在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为60°,此时他距地面的高度AE为21米,电梯再上升9米到达D点,此时测得大楼BC楼顶B点的仰角为45°,求大楼BC的高度.(结果保留根号)
【分析】过D作DH⊥BC于H,过E作EG⊥BC于G.求出EG和DH的长,在Rt△BDH中,求出BH,则可得出答案
【解答】解:过D作DH⊥BC于H,过E作EG⊥BC于G.
由已知得,∠BDH=45°,∠CEG=60°,AE=21米,DE=9米.
在Rt△CEG中,CG=AE=21米,tan∠CEG=,
∴EG===7(米).
∴DH=EG=7米.
在Rt△BDH中,∵∠BDH=45°,
∴BH=DH=7米.
∴BC=CG+HG+BH=CG+DE+BH=21+9+7=(30+7)米.
答:大楼BC的高度是(30+7)米.
21.(8分)如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
(1)求改造前坡顶与地面的距离BE的长;
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
【参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75】
【分析】(1)根据i的值,设出BE与AE,由AB的长求出k的值,即可确定出AE与BE;
(2)过点F作FG⊥AD于点G,由题意,利用锐角三角函数定义求出AG的长,由AG﹣AE求出BF的长即可.
【解答】解:(1)在Rt△ABE中,AB=26,i==,
设BE=12k,AE=5k,则AB=13k=26,k=2,
∴AE=10(米),BE=24(米);
(2)过点F作FG⊥AD于点G,
由题意可知:FG=BE=24,∠FAD=53°,
在Rt△AFG中,cot53°==0.75,
∴AG=18(米),
∴BF=GE=AG﹣AE=8(米),
答:改造前坡顶与地面的距离BE为24米;BF至少是8米.
22.(10分)在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
【分析】(1)有顶点就用顶点式来求二次函数的解析式;
(2)由于是向右平移,可让二次函数的y的值为0,得到相应的两个x值,算出负值相对于原点的距离,而后让较大的值也加上距离即可.
【解答】解:(1)∵二次函数图象的顶点为A(1,﹣4),
∴设二次函数解析式为y=a(x﹣1)2﹣4,
把点B(3,0)代入二次函数解析式,得:
0=4a﹣4,解得a=1,
∴二次函数解析式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3;
(2)令y=0,得x2﹣2x﹣3=0,解方程,得x1=3,x2=﹣1.
∴二次函数图象与x轴的两个交点坐标分别为(3,0)和(﹣1,0),
∴二次函数图象上的点(﹣1,0)向右平移1个单位后经过坐标原点或向右平移﹣3个单位,
故平移后所得图象与x轴的另一个交点坐标为(4,0)或(﹣4,0).
23.(10分)“佳佳商场”在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,“佳佳商场”应将这种商品的售价定为多少?
(2)物价局规定该商品的售价不能超过40元/件,“佳佳商场”为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
【分析】(1)设商品的定价为x元,由这种商品的售价每上涨1元,其销售量就减少2件,列出等式求得x的值即可;
(2)设利润为y元,列出二次函数关系式,在售价不超过40元/件的范围内求得利润的最大值.
【解答】解:(1)设商品的定价为x元,由题意,得
(x﹣20)[100﹣2(x﹣30)]=1600,
解得:x=40或x=60;
答:售价应定为40元或60元.
(2)设利润为y元,得:
y=(x﹣20)[100﹣2(x﹣30)](x≤40),
即:y=﹣2x2+200x﹣3200;
∵a=﹣2<0,
∴当x=﹣=﹣=50时,y取得最大值;
又x≤40,则在x=40时可取得最大值,
即y最大=1600.
答:售价为40元/件时,此时利润最大,最大为1600元.
24.(10分)如图,一次函数y1=ax+b与反比例函数y2=的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围为 x>8或0<x<2 ;
(3)点P是x轴上一点,当S△PAC=S△AOB时,请直接写出点P的坐标为 P(3,0)或P(﹣3,0) .
【分析】(1)由待定系数法即可得到结论;
(2)根据图象中的信息即可得到结论;
(3)先求得D的坐标,然后根据S△AOB=S△AOD﹣S△BOD求得△AOB的面积,即可求得S△PAC=S△AOB=24,根据中心对称的性质得出OA=OC,即可得到S△APC=2S△AOP,从而得到2×OP×8=24,求得OP,即可求得P的坐标.
【解答】解:(1)将A(2,8),B(8,2)代入y=ax+b得,
解得,
∴一次函数为y=﹣x+10,
将A(2,8)代入y2=得8=,解得k=16,
∴反比例函数的解析式为y=;
(2)由图象可知,当y1<y2时,自变量x的取值范围为:x>8或0<x<2,
故答案为x>8或0<x<2;
(3)由题意可知OA=OC,
∴S△APC=2S△AOP,
把y=0代入y1=﹣x+10得,0=﹣x+10,解得x=10,
∴D(10,0),
∴S△AOB=S△AOD﹣S△BOD=﹣=30,
∵S△PAC=S△AOB=×30=24,
∴2S△AOP=24,
∴2××yA=24,即2×OP×8=24,
∴OP=3,
∴P(3,0)或P(﹣3,0),
故答案为P(3,0)或P(﹣3,0).
25.(12分)如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为2?若存在求出点Q的坐标;若不存在请说明理由.
【分析】(1)可设抛物线解析式为顶点式,由B点坐标可求得抛物线的解析式,则可求得D点坐标,利用待定系数法可求得直线BD解析式;
(2)设出P点坐标,从而可表示出PM的长度,利用二次函数的性质可求得其最大值;
(3)过Q作QG∥y轴,交BD于点G,过Q和QH⊥BD于H,可设出Q点坐标,表示出QG的长度,由条件可证得△DHG为等腰直角三角形,则可得到关于Q点坐标的方程,可求得Q点坐标.
【解答】解:
(1)∵抛物线的顶点C的坐标为(1,4),
∴可设抛物线解析式为y=a(x﹣1)2+4,
∵点B(3,0)在该抛物线的图象上,
∴0=a(3﹣1)2+4,解得a=﹣1,
∴抛物线解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3,
∵点D在y轴上,令x=0可得y=3,
∴D点坐标为(0,3),
∴可设直线BD解析式为y=kx+3,
把B点坐标代入可得3k+3=0,解得k=﹣1,
∴直线BD解析式为y=﹣x+3;
(2)设P点横坐标为m(m>0),则P(m,﹣m+3),M(m,﹣m2+2m+3),
∴PM=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣)2+,
∴当m=时,PM有最大值;
(3)如图,过Q作QG∥y轴交BD于点G,交x轴于点E,作QH⊥BD于H,
设Q(x,﹣x2+2x+3),则G(x,﹣x+3),
∴QG=|﹣x2+2x+3﹣(﹣x+3)|=|﹣x2+3x|,
∵△BOD是等腰直角三角形,
∴∠DBO=45°,
∴∠HGQ=∠BGE=45°,
当△BDQ中BD边上的高为2时,即QH=HG=2,
∴QG=×2=4,
∴|﹣x2+3x|=4,
当﹣x2+3x=4时,△=9﹣16<0,方程无实数根,
当﹣x2+3x=﹣4时,解得x=﹣1或x=4,
∴Q(﹣1,0)或(4,﹣5),
综上可知存在满足条件的点Q,其坐标为(﹣1,0)或(4,﹣5).
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.(3分)若函数y=(k≠0)的图象过点(1,),则此函数图象位于( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
2.(3分)已知反比例函数y=﹣,下列结论不正确的是( )
A.图象必经过点(﹣1,2) B.若x>1,则y>﹣2
C.图象在第二、四象限内 D.y随x的增大而增大
3.(3分)对于二次函数y=(x+1)2+2的图象,下列说法正确的是( )
A.开口向下 B.对称轴是直线x=﹣1
C.顶点坐标是(1,2) D.与x轴有两个交点
4.(3分)如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )
A. B. C. D.
5.(3分)若抛物线是关于x的二次函数,那么m的值是( )
A.3 B.﹣2 C.2 D.2或3
6.(3分)在Rt△ACB中,∠C=90°,,则sinB的值为( )
A. B. C. D.
7.(3分)若代数式有意义,则实数x的取值范围是( )
A.x≥﹣1 B.x≥﹣1且x≠3 C.x>﹣1 D.x>﹣1且x≠3
8.(3分)已知点A(﹣3,y1),B(2,y2),C(3,y3)在抛物线y=2x2﹣4x+c上,则y1、y2、y3的大小关系是( )
A.y1>y2>y3 B.y1>y3>y2 C.y3>y2>y1 D.y2>y3>y1
9.(3分)如果二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=在同一坐标系中的图象大致是( )
A. B.
C. D.
10.(3分)如图,O是坐标原点, OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数(x<0)的图象经过顶点B,则S OABC的值为( )
A.27 B.15 C.12 D.无法确定
11.(3分)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,直线x=1是它的对称轴,有下列5个结论:①abc>0;②4a+2b+c>0;③b2﹣4ac>0;④2a﹣b=0;⑤方程ax2+bx+c﹣3=0有两个相等的实数根.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
12.(3分)如图,点A、C在反比例函数y=的图象上,点B、D在反比例函数y=的图象上,a>b>0,AB∥CD∥x轴,AB、CD在x轴的两侧,AB=,CD=,AB、CD的距离为6,则a﹣b的值为( )
A.3 B. C.﹣3 D.无法确定
二、填空题
13.(3分)如图抛物线y=ax2与反比例函数交于点C(1,2),则不等式的解集是 .
14.(3分)△ABC中,∠A、∠B都是锐角,若sinA=,cosB=,则∠C= .
15.(3分)若函数y=(1﹣m)+2是关于x的二次函数,且抛物线的开口向上,则m的值为 .
16.(3分)如图,正方形ABCD的顶点A、D分别在x轴、y轴上,∠ADO=30°,OA=2,反比例函数y=经过CD的中点M,那么k= .
17.(3分)如图所示,点A是反比侧函数图象上一点.过点A作AB⊥x轴于点B.若OA=5,则△AOB的周长为 .
18.(3分)如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=(x>0)的图象上,则经过点B的反比例函数解析式为 .
三、解答题(本大题共7小题,共66分.解答应写出文字说明、证明过程或演算步骤.)
19.(8分)计算:
(1);
(2)2﹣2﹣+6sin45°﹣.
20.(8分)如图,小亮在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为60°,此时他距地面的高度AE为21米,电梯再上升9米到达D点,此时测得大楼BC楼顶B点的仰角为45°,求大楼BC的高度.(结果保留根号)
21.(8分)如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
(1)求改造前坡顶与地面的距离BE的长;
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
【参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75】
22.(10分)在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
23.(10分)“佳佳商场”在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,“佳佳商场”应将这种商品的售价定为多少?
(2)物价局规定该商品的售价不能超过40元/件,“佳佳商场”为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
24.(10分)如图,一次函数y1=ax+b与反比例函数y2=的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围为 ;
(3)点P是x轴上一点,当S△PAC=S△AOB时,请直接写出点P的坐标为 .
25.(12分)如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为2?若存在求出点Q的坐标;若不存在请说明理由.
2021-2022学年山东省济南市莱芜实验中学片区教研共同体九年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.(3分)若函数y=(k≠0)的图象过点(1,),则此函数图象位于( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
【分析】先由已知点求出k的值,然后得到函数图象所在的象限.
【解答】解:∵函数y=(k≠0)的图象过点(1,),
∴k=1×=>0,
∴函数图象位于第一、三象限.
故选:B.
2.(3分)已知反比例函数y=﹣,下列结论不正确的是( )
A.图象必经过点(﹣1,2) B.若x>1,则y>﹣2
C.图象在第二、四象限内 D.y随x的增大而增大
【分析】根据反比例函数的性质:当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大进行分析即可.
【解答】解:A、图象必经过点(﹣1,2),说法正确,不合题意;
B、若x>1,则﹣2<y<0,说法错误,符合题意;
C、k=﹣2<0,图象在第二、四象限内,说法正确,不合题意;
D、k=﹣2<0,每个象限内,y随x的增大而增大,说法正确,不合题意;
故选:B.
3.(3分)对于二次函数y=(x+1)2+2的图象,下列说法正确的是( )
A.开口向下 B.对称轴是直线x=﹣1
C.顶点坐标是(1,2) D.与x轴有两个交点
【分析】根据a的正负判断开口方向,通过抛物线的y=a(x﹣h)2+k解析式判定对称轴、顶点坐标,根据顶点坐标和开口方向即可判断抛物线与x轴交点个数.
【解答】解:∵抛物线a>0,所以开口向上,A选项错误;顶点坐标为(﹣1,2),所以C选项错误;
根据顶点坐标以及开口向上可判定与x轴没有交点,
∴D选项错误;
对称轴为直线x=﹣1,B选项正确.
故选:B.
4.(3分)如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )
A. B. C. D.
【分析】直接连接DC,得出CD⊥AB,再结合勾股定理以及锐角三角函数关系得出答案
【解答】解:连接DC,
由网格可得:CD⊥AB,
则DC=,AC=,
故sinA=.
故选:D.
5.(3分)若抛物线是关于x的二次函数,那么m的值是( )
A.3 B.﹣2 C.2 D.2或3
【分析】根据二次函数的最高指数是2,二次项系数不等于0列出方程求解即可.
【解答】解:由题意得,m2﹣5m+8=2且m﹣3≠0,
解得m1=2,m2=3,且m≠3,
所以,m=2.
故选:C.
6.(3分)在Rt△ACB中,∠C=90°,,则sinB的值为( )
A. B. C. D.
【分析】根据锐角三角函数的定义进行计算即可.
【解答】解:设Rt△ACB中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,
由于tanA==2,
可设a=2k,b=k,由勾股定理得,
c==5k,
∴sinB==,
故选:A.
7.(3分)若代数式有意义,则实数x的取值范围是( )
A.x≥﹣1 B.x≥﹣1且x≠3 C.x>﹣1 D.x>﹣1且x≠3
【分析】根据被开方数大于等于0,分母不等于0列式计算即可得解.
【解答】解:由题意得,x+1≥0且x﹣3≠0,
解得:x≥﹣1且x≠3.
故选:B.
8.(3分)已知点A(﹣3,y1),B(2,y2),C(3,y3)在抛物线y=2x2﹣4x+c上,则y1、y2、y3的大小关系是( )
A.y1>y2>y3 B.y1>y3>y2 C.y3>y2>y1 D.y2>y3>y1
【分析】先配方得到抛物线的对称轴为直线x=1,根据二次函数的性质,通过三点与对称轴距离的远近来比较函数值的大小.
【解答】解:y=2x2﹣4x+c=2(x﹣1)2+c﹣2,
则抛物线的对称轴为直线x=1,
∵抛物线开口向上,点A(﹣3,y1)到对称轴的距离最远,点B(2,y2)到对称轴的距离最近,
∴y1>y3>y2.
故选:B.
9.(3分)如果二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=在同一坐标系中的图象大致是( )
A. B.
C. D.
【分析】根据二次函数的图象的性质先确定出a、b、c的取值范围,然后根据一次函数和反比例函数的性质即可做出判断.
【解答】解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴由于y轴的左侧;
∴a与b同号,
∴b<0,
∵抛物线经过原点,所以c=0.
∵b<0,c=0,
∴直线y=bx+c经过二、四象限和坐标原点.
∵b<0,
∴反比例函数的图象,位于二、四象限.
故选:A.
10.(3分)如图,O是坐标原点, OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数(x<0)的图象经过顶点B,则S OABC的值为( )
A.27 B.15 C.12 D.无法确定
【分析】过点A作AD⊥y轴于点D,过点B作BE⊥x轴于点E,根据反比例函数系数k的几何意义得S矩形BDOE=27,进而求得BD,进一步得到AB,根据矩形面积公式即可求得答案.
【解答】解:过点A作AD⊥y轴于点D,过点B作BE⊥x轴于点E,
∵函数(x<0)的图象经过顶点B,
∴S矩形BDOE=27,
∵ OABC的顶点A的坐标为(﹣3,4),
∴AD=3,DO=4,
∴BD OA=27,即BD×4=27,
∴BD=,
∴OC=AB=﹣3=,
∴S OABC=OC OD=15,
故选:B.
11.(3分)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,直线x=1是它的对称轴,有下列5个结论:①abc>0;②4a+2b+c>0;③b2﹣4ac>0;④2a﹣b=0;⑤方程ax2+bx+c﹣3=0有两个相等的实数根.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据二次函数的图象与性质即可求出答案.
【解答】解:①由图象可知:a<0,c>0,
>0,
∴b>0,
∴abc<0,故①错误;
②抛物线的对称轴为x=1,
∴(﹣1,y)关于直线x=1的对称点为(3,y),
(0,c)关于直线x=1的对称点为(2,c)
∴x=2,y=4a+2b+c>0,故②正确;
③抛物线与x轴有两个交点,
∴Δ=b2﹣4ac>0,故③正确;
④由对称轴可知:=1,
∴2a+b=0,故④错误;
⑤由图象可知:y=3时,
此时ax2+bx+c=3只有一解x=1,
∴方程ax2+bx+c﹣3=0有两个相同的根,故⑤正确;
故选:C.
12.(3分)如图,点A、C在反比例函数y=的图象上,点B、D在反比例函数y=的图象上,a>b>0,AB∥CD∥x轴,AB、CD在x轴的两侧,AB=,CD=,AB、CD的距离为6,则a﹣b的值为( )
A.3 B. C.﹣3 D.无法确定
【分析】设点A、B的纵坐标为y1,点C、D的纵坐标为y2,分别表示出来A、B、C、D四点的坐标,根据线段AB、CD的长度结合AB与CD间的距离,即可得出y1、y2的值,再由点A、B的横坐标结合AB=即可求出a﹣b的值.
【解答】解:设点A、B的纵坐标为y1(y1>0),点C、D的纵坐标为y2(y2<0),则点A(,y1),点B(,y1),
∵AB=,CD=,
∴2×||=||,
∴|y1|=2|y2|.
∵|y1|+|y2|=6,
∴y1=4,y2=﹣2.
∴AB=﹣==,
∴a﹣b=3.
故选:A.
二、填空题
13.(3分)如图抛物线y=ax2与反比例函数交于点C(1,2),则不等式的解集是 x<0或x>1 .
【分析】结合函数图象即可得出解集.
【解答】解:由图可知,当x<0或x>1时抛物线y=ax2在反比例函数图象的上方,
当0<x<1时,抛物线y=ax2在反比例函数图象的下方,
∴不等式的解集是x<0或x>1.
故答案为:x<0或x>1.
14.(3分)△ABC中,∠A、∠B都是锐角,若sinA=,cosB=,则∠C= 60° .
【分析】先根据特殊角的三角函数值求出∠A、∠B的度数,再根据三角形内角和定理求出∠C即可作出判断.
【解答】解:∵△ABC中,∠A、∠B都是锐角sinA=,cosB=,
∴∠A=∠B=60°.
∴∠C=180°﹣∠A﹣∠B=180°﹣60°﹣60°=60°.
故答案为:60°.
15.(3分)若函数y=(1﹣m)+2是关于x的二次函数,且抛物线的开口向上,则m的值为 ﹣2 .
【分析】先依据二次函数的定义知,系数1﹣m一定不为0,1﹣m>0,再得出m2﹣2=2,求出m的值即可.
【解答】解:由题意得:1﹣m≠0,
解得:m≠1,
∵抛物线的开口向上,
∴1﹣m>0,
解得:m<1,
∵m2﹣2=2,
∴解得:m=±2,
∴m=﹣2.
故答案为:﹣2.
16.(3分)如图,正方形ABCD的顶点A、D分别在x轴、y轴上,∠ADO=30°,OA=2,反比例函数y=经过CD的中点M,那么k= +6 .
【分析】作CE⊥y轴于点E,先证明△CDE≌△DAO,得到DE=AO=2,DO=2=CE,再根据M是CD的中点,即可得到M(,1+2),最后根据反比例函数y=经过CD的中点M,即可得到k的值.
【解答】解:如图,作CE⊥y轴于点E.
∵正方形ABCD的顶点A、D分别在x轴、y轴上,
∴∠CED=∠DOA=90°,∠DCE=∠ADO,CD=DA,
∴△CDE≌△DAO(AAS),
∴DE=AO=2,
又∵∠ODA=30°,
∴Rt△AOD中,AD=2AO=4,DO=2=CE,
∴EO=2+2,
∴C(2,2+2),D(0,2),
∵M是CD的中点,
∴M(,1+2),
∵反比例函数y=经过CD的中点M,
∴k=(1+2)=+6,
故答案为:+6.
17.(3分)如图所示,点A是反比侧函数图象上一点.过点A作AB⊥x轴于点B.若OA=5,则△AOB的周长为 12 .
【分析】设A的坐标是(a,﹣b),则ab=12,在直角△AOB中利用勾股定理即可求得a2+b2的值,利用完全平方式即可求得a+b的值,即直角三角形的两直角边的长,则周长即可求得.
【解答】解:设A的坐标是(a,﹣b),则ab=12,
∵OA=5,
∴a2+b2=25,
∴(a+b)2=a2+b2+2ab=25+24=49,
∵a+b>0,
∴a+b=7,
故△AOB的周长是:7+5=12.
故答案是:12.
18.(3分)如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=(x>0)的图象上,则经过点B的反比例函数解析式为 y=﹣ .
【分析】过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D,证明△BCO∽△ODA,利用相似三角形的判定与性质得出=,根据反比例函数图象上点的坐标特征得出S△AOD=3,那么S△BCO=1,进而得出答案.
【解答】解:过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D,如图.
∵∠BOA=90°,
∴∠BOC+∠AOD=90°,
∵∠AOD+∠OAD=90°,
∴∠BOC=∠OAD,
又∵∠BCO=∠ADO=90°,
∴△BCO∽△ODA,
∴=tan30°=,
∴=,
∵×AD×DO=xy=3,
∴S△BCO=×BC×CO=S△AOD=1,
∵经过点B的反比例函数图象在第二象限,
故反比例函数解析式为:y=﹣.
故答案为y=﹣.
三、解答题(本大题共7小题,共66分.解答应写出文字说明、证明过程或演算步骤.)
19.(8分)计算:
(1);
(2)2﹣2﹣+6sin45°﹣.
【分析】(1)先分母有理化、代入三角函数、计算二次根式的乘法,再计算加减即可;
(2)先计算负整数指数幂、代入三角函数值、利用二次根式的性质化简,再计算乘法,最后计算加减即可.
【解答】解:(1)原式=﹣+
=﹣+2
=﹣+2
=;
(2)原式=﹣2+6×﹣3
=﹣2+3﹣3
=﹣.
20.(8分)如图,小亮在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为60°,此时他距地面的高度AE为21米,电梯再上升9米到达D点,此时测得大楼BC楼顶B点的仰角为45°,求大楼BC的高度.(结果保留根号)
【分析】过D作DH⊥BC于H,过E作EG⊥BC于G.求出EG和DH的长,在Rt△BDH中,求出BH,则可得出答案
【解答】解:过D作DH⊥BC于H,过E作EG⊥BC于G.
由已知得,∠BDH=45°,∠CEG=60°,AE=21米,DE=9米.
在Rt△CEG中,CG=AE=21米,tan∠CEG=,
∴EG===7(米).
∴DH=EG=7米.
在Rt△BDH中,∵∠BDH=45°,
∴BH=DH=7米.
∴BC=CG+HG+BH=CG+DE+BH=21+9+7=(30+7)米.
答:大楼BC的高度是(30+7)米.
21.(8分)如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
(1)求改造前坡顶与地面的距离BE的长;
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
【参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75】
【分析】(1)根据i的值,设出BE与AE,由AB的长求出k的值,即可确定出AE与BE;
(2)过点F作FG⊥AD于点G,由题意,利用锐角三角函数定义求出AG的长,由AG﹣AE求出BF的长即可.
【解答】解:(1)在Rt△ABE中,AB=26,i==,
设BE=12k,AE=5k,则AB=13k=26,k=2,
∴AE=10(米),BE=24(米);
(2)过点F作FG⊥AD于点G,
由题意可知:FG=BE=24,∠FAD=53°,
在Rt△AFG中,cot53°==0.75,
∴AG=18(米),
∴BF=GE=AG﹣AE=8(米),
答:改造前坡顶与地面的距离BE为24米;BF至少是8米.
22.(10分)在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
【分析】(1)有顶点就用顶点式来求二次函数的解析式;
(2)由于是向右平移,可让二次函数的y的值为0,得到相应的两个x值,算出负值相对于原点的距离,而后让较大的值也加上距离即可.
【解答】解:(1)∵二次函数图象的顶点为A(1,﹣4),
∴设二次函数解析式为y=a(x﹣1)2﹣4,
把点B(3,0)代入二次函数解析式,得:
0=4a﹣4,解得a=1,
∴二次函数解析式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3;
(2)令y=0,得x2﹣2x﹣3=0,解方程,得x1=3,x2=﹣1.
∴二次函数图象与x轴的两个交点坐标分别为(3,0)和(﹣1,0),
∴二次函数图象上的点(﹣1,0)向右平移1个单位后经过坐标原点或向右平移﹣3个单位,
故平移后所得图象与x轴的另一个交点坐标为(4,0)或(﹣4,0).
23.(10分)“佳佳商场”在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,“佳佳商场”应将这种商品的售价定为多少?
(2)物价局规定该商品的售价不能超过40元/件,“佳佳商场”为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
【分析】(1)设商品的定价为x元,由这种商品的售价每上涨1元,其销售量就减少2件,列出等式求得x的值即可;
(2)设利润为y元,列出二次函数关系式,在售价不超过40元/件的范围内求得利润的最大值.
【解答】解:(1)设商品的定价为x元,由题意,得
(x﹣20)[100﹣2(x﹣30)]=1600,
解得:x=40或x=60;
答:售价应定为40元或60元.
(2)设利润为y元,得:
y=(x﹣20)[100﹣2(x﹣30)](x≤40),
即:y=﹣2x2+200x﹣3200;
∵a=﹣2<0,
∴当x=﹣=﹣=50时,y取得最大值;
又x≤40,则在x=40时可取得最大值,
即y最大=1600.
答:售价为40元/件时,此时利润最大,最大为1600元.
24.(10分)如图,一次函数y1=ax+b与反比例函数y2=的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围为 x>8或0<x<2 ;
(3)点P是x轴上一点,当S△PAC=S△AOB时,请直接写出点P的坐标为 P(3,0)或P(﹣3,0) .
【分析】(1)由待定系数法即可得到结论;
(2)根据图象中的信息即可得到结论;
(3)先求得D的坐标,然后根据S△AOB=S△AOD﹣S△BOD求得△AOB的面积,即可求得S△PAC=S△AOB=24,根据中心对称的性质得出OA=OC,即可得到S△APC=2S△AOP,从而得到2×OP×8=24,求得OP,即可求得P的坐标.
【解答】解:(1)将A(2,8),B(8,2)代入y=ax+b得,
解得,
∴一次函数为y=﹣x+10,
将A(2,8)代入y2=得8=,解得k=16,
∴反比例函数的解析式为y=;
(2)由图象可知,当y1<y2时,自变量x的取值范围为:x>8或0<x<2,
故答案为x>8或0<x<2;
(3)由题意可知OA=OC,
∴S△APC=2S△AOP,
把y=0代入y1=﹣x+10得,0=﹣x+10,解得x=10,
∴D(10,0),
∴S△AOB=S△AOD﹣S△BOD=﹣=30,
∵S△PAC=S△AOB=×30=24,
∴2S△AOP=24,
∴2××yA=24,即2×OP×8=24,
∴OP=3,
∴P(3,0)或P(﹣3,0),
故答案为P(3,0)或P(﹣3,0).
25.(12分)如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为2?若存在求出点Q的坐标;若不存在请说明理由.
【分析】(1)可设抛物线解析式为顶点式,由B点坐标可求得抛物线的解析式,则可求得D点坐标,利用待定系数法可求得直线BD解析式;
(2)设出P点坐标,从而可表示出PM的长度,利用二次函数的性质可求得其最大值;
(3)过Q作QG∥y轴,交BD于点G,过Q和QH⊥BD于H,可设出Q点坐标,表示出QG的长度,由条件可证得△DHG为等腰直角三角形,则可得到关于Q点坐标的方程,可求得Q点坐标.
【解答】解:
(1)∵抛物线的顶点C的坐标为(1,4),
∴可设抛物线解析式为y=a(x﹣1)2+4,
∵点B(3,0)在该抛物线的图象上,
∴0=a(3﹣1)2+4,解得a=﹣1,
∴抛物线解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3,
∵点D在y轴上,令x=0可得y=3,
∴D点坐标为(0,3),
∴可设直线BD解析式为y=kx+3,
把B点坐标代入可得3k+3=0,解得k=﹣1,
∴直线BD解析式为y=﹣x+3;
(2)设P点横坐标为m(m>0),则P(m,﹣m+3),M(m,﹣m2+2m+3),
∴PM=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣)2+,
∴当m=时,PM有最大值;
(3)如图,过Q作QG∥y轴交BD于点G,交x轴于点E,作QH⊥BD于H,
设Q(x,﹣x2+2x+3),则G(x,﹣x+3),
∴QG=|﹣x2+2x+3﹣(﹣x+3)|=|﹣x2+3x|,
∵△BOD是等腰直角三角形,
∴∠DBO=45°,
∴∠HGQ=∠BGE=45°,
当△BDQ中BD边上的高为2时,即QH=HG=2,
∴QG=×2=4,
∴|﹣x2+3x|=4,
当﹣x2+3x=4时,△=9﹣16<0,方程无实数根,
当﹣x2+3x=﹣4时,解得x=﹣1或x=4,
∴Q(﹣1,0)或(4,﹣5),
综上可知存在满足条件的点Q,其坐标为(﹣1,0)或(4,﹣5).
同课章节目录
