2021-2022学年湖南省岳阳市汨罗市弼时片八年级(上)期中数学试卷 (Word版含解析)
文档属性
| 名称 | 2021-2022学年湖南省岳阳市汨罗市弼时片八年级(上)期中数学试卷 (Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 301.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-15 09:00:03 | ||
图片预览




文档简介
2021-2022学年湖南省岳阳市汨罗市弼时片八年级(上)期中数学试卷
一、选择题(每小题有且只有一个正确答案,本题共8小题,每小题3分,共24分)
1.(3分)下列分式是最简分式的是( )
A. B.
C. D.
2.(3分)有下列命题:①两点之间,线段最短;②相等的角是对顶角;③当a≥0时,|a|=a;④内错角互补,两直线平行.其中是真命题的有( )
A.1个 B.2个 C.3个 D.4个
3.(3分)若分式的值为0,则x的值为( )
A.0 B.1 C.﹣1 D.±1
4.(3分)要使分式有意义,则x应满足的条件是( )
A.x≠1 B.x≠﹣1 C.x≠0 D.x>1
5.(3分)下列运算正确的是( )
A.(x3)2=x5 B.(﹣x)5=﹣x5
C.x3 x2=x6 D.3x2+2x3=5x5
6.(3分)某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
7.(3分)如图,△ABC≌△BAD,点A和点B,点C和点D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB度数是( )
A.80° B.70° C.60° D.50°
8.(3分)货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是( )
A. B. C. D.
二、填空题(本题共8小题,每小题4分,共24分)
9.(4分)计算:(a﹣2)3= .
10.(4分)计算:+= .
11.(4分)如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B= .
12.(4分)已知关于x的方程会产生增根,则k的值为 .
13.(4分)每年四月北京很多地方杨絮、柳絮如雪花般飞舞.据测定,杨絮纤维的直径约为0.0000105米,将0.0000105用科学记数法可表示为 .
14.(4分)等腰三角形的两边的长分别为5cm和7cm,则此三角形的周长是 .
15.(4分)在△ABC中,∠A=70°,∠A比∠B大10°,则∠C= °.
16.(4分)如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件是 (填上你认为适当的一个条件即可).
三、解答题(本大题共8小题,共56分)
17.(6分)计算:(﹣)﹣1﹣2+(π﹣3.14)0.
18.(6分)解方程:.
19.(8分)先化简,再求值:.选一个你所喜欢的数代入求值.
20.(8分)观察下面的变形规律:
=1﹣;=﹣;=﹣;……解答下面的问题:
(1)若n为正整数,请你猜想= .
(2)若n为正整数,请你用所学的知识证明﹣=.
(3)求和:+++…+.
21.(8分)如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,求AC的长.
22.(8分)如图,D、E在BC上,且BD=CE,AD=AE,∠ADE=∠AED,求证:AB=AC.
23.(10分)为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买A种图书花费了3000元,购买B种图书花费了1600元,A种图书的单价是B种图书的1.5倍,购买A种图书的数量比B种图书多20本.
(1)求A和B两种图书的单价;
(2)书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了A种图书20本和B种图书25本,共花费多少元?
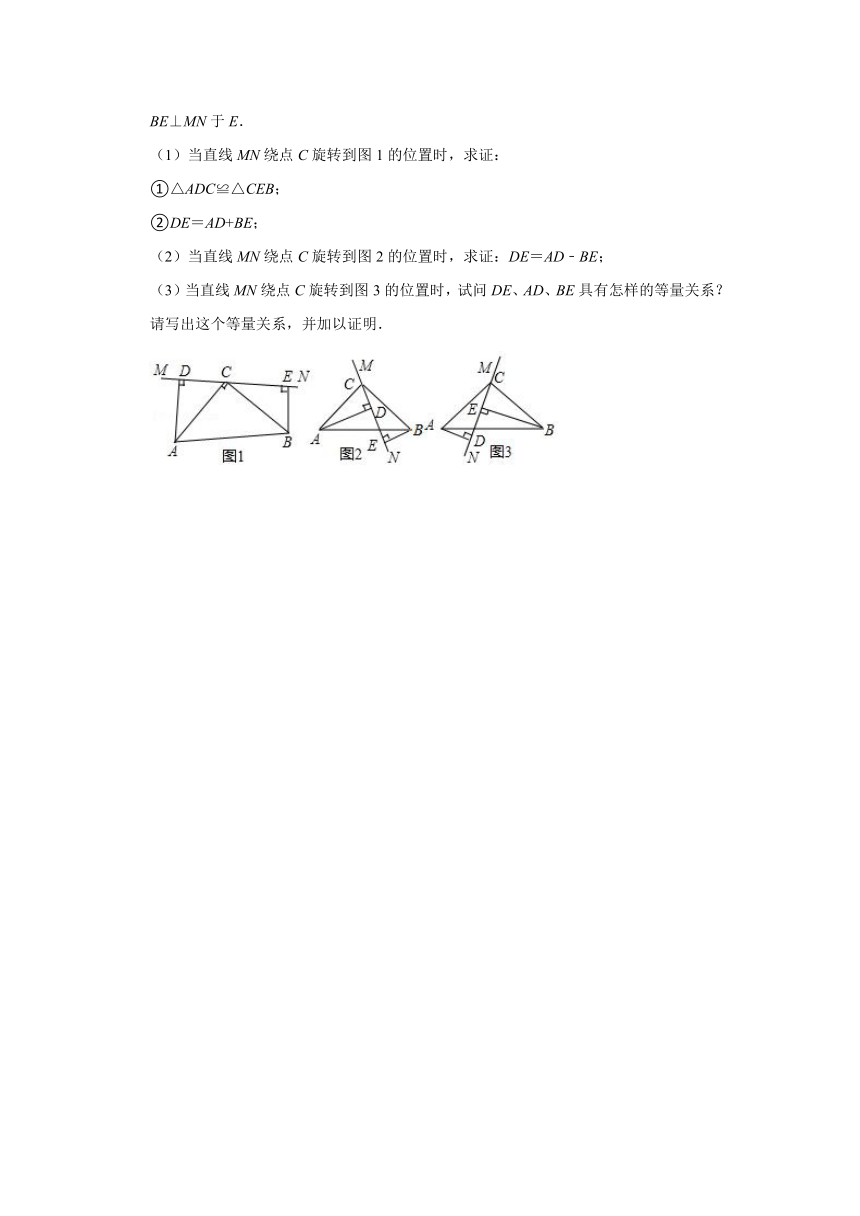
24.(10分)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
2021-2022学年湖南省岳阳市汨罗市弼时片八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(每小题有且只有一个正确答案,本题共8小题,每小题3分,共24分)
1.(3分)下列分式是最简分式的是( )
A. B.
C. D.
【分析】利用最简分式定义:分子分母没有公因式的分式,判断即可.
【解答】解:A、原分式的分子分母中不含有公因式,故此选项符合题意;
B、原式=,故此选项不符合题意;
C、原式=,故此选项不符合题意;
D、原式=,故此选项不符合题意;
故选:A.
2.(3分)有下列命题:①两点之间,线段最短;②相等的角是对顶角;③当a≥0时,|a|=a;④内错角互补,两直线平行.其中是真命题的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据两点之间线段最短、对顶角的概念、绝对值的性质、平行线的判定定理判断即可.
【解答】解:①两点之间,线段最短,本说法是真命题;
②相等的角不一定是对顶角,本小题说法是假命题;
③当a≥0时,|a|=a,本说法是真命题;
④内错角相等,两直线平行,本小题说法是假命题;
故选:B.
3.(3分)若分式的值为0,则x的值为( )
A.0 B.1 C.﹣1 D.±1
【分析】根据分式为0的条件列出关于x的不等式组,求出x的值即可.
【解答】解:∵分式的值为零,
∴,解得x=1.
故选:B.
4.(3分)要使分式有意义,则x应满足的条件是( )
A.x≠1 B.x≠﹣1 C.x≠0 D.x>1
【分析】本题主要考查分式有意义的条件:分母不能为0.
【解答】解:∵x+1≠0,
∴x≠﹣1.
故选:B.
5.(3分)下列运算正确的是( )
A.(x3)2=x5 B.(﹣x)5=﹣x5
C.x3 x2=x6 D.3x2+2x3=5x5
【分析】根据幂的乘方,同底数幂的乘法以及合并同类项计算法则进行解答.
【解答】解:A、原式=x6,故本选项错误;
B、原式=﹣x5,故本选项正确;
C、原式=x5,故本选项错误;
D、3x2与2x3不是同类项,不能合并,故本选项错误;
故选:B.
6.(3分)某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
【分析】本题就是已知三角形破损部分的边角,得到原来三角形的边角,根据三角形全等的判定方法,即可求解.
【解答】解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;
第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去.
故选:C.
7.(3分)如图,△ABC≌△BAD,点A和点B,点C和点D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB度数是( )
A.80° B.70° C.60° D.50°
【分析】根据全等三角形的性质得到∠DBA=∠CAB=50°,根据三角形内角和定理计算即可.
【解答】解:△ABC≌△BAD,点A和点B,点C和点D是对应点,
∴∠DBA=∠CAB=50°,
∴∠DAB=180°﹣70°﹣50°=60°,
故选:C.
8.(3分)货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是( )
A. B. C. D.
【分析】题中等量关系:货车行驶25千米与小车行驶35千米所用时间相同,列出关系式.
【解答】解:根据题意,得
.
故选:C.
二、填空题(本题共8小题,每小题4分,共24分)
9.(4分)计算:(a﹣2)3= a﹣6 .
【分析】根据负整数指数幂的运算法则进行计算即可.
【解答】解:(a﹣2)3=a﹣6.
故答案为:a﹣6.
10.(4分)计算:+= 0 .
【分析】原式变形后,利用同分母分式的减法法则计算即可得到结果.
【解答】解:原式=﹣=0,
故答案为:0
11.(4分)如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B= 70° .
【分析】根据三角形的外角等于与它不相邻的两个内角和,即可得出∠B的度数.
【解答】解:∵∠ACD=∠A+∠B,∠A=80°,∠ACD=150°,
∴∠B=70°.
故答案为:70°.
12.(4分)已知关于x的方程会产生增根,则k的值为 8 .
【分析】首先让最简公分母x﹣4=0,得到x=4,然后代入化为整式方程的方程,求出k的值是多少即可.
【解答】解:方程两边都乘(x﹣4),
可得:2x=k,
∵原方程有增根,
∴x﹣4=0,
解得x=4,
当x=4时,k=2×4=8.
故答案为:8.
13.(4分)每年四月北京很多地方杨絮、柳絮如雪花般飞舞.据测定,杨絮纤维的直径约为0.0000105米,将0.0000105用科学记数法可表示为 1.05×10﹣5 .
【分析】绝对值小于1的负数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.0000105=1.05×10﹣5.
故答案为:1.05×10﹣5.
14.(4分)等腰三角形的两边的长分别为5cm和7cm,则此三角形的周长是 17cm或19cm .
【分析】根据等腰三角形的性质,分两种情况:①当腰长为5cm时,②当腰长为7cm时,解答出即可.
【解答】解:根据题意,
①当腰长为5cm时,周长=5+5+7=17(cm);
②当腰长为7cm时,周长=5+7+7=19(cm);
故答案为:17cm或19cm.
15.(4分)在△ABC中,∠A=70°,∠A比∠B大10°,则∠C= 50 °.
【分析】由题意可得∠B=60°,利用三角形的内角和定理即可求∠C.
【解答】解:∵∠A=70°,∠A比∠B大10°,
∴∠B=∠A﹣10°=60°,
∴∠C=180°﹣∠A﹣∠B=50°.
故答案为:50.
16.(4分)如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件是 ∠B=∠C (填上你认为适当的一个条件即可).
【分析】根据题意,易得∠AEB=∠AEC,又AE公共,所以根据全等三角形的判定方法容易寻找添加条件.
【解答】解:∵∠1=∠2,∴∠AEB=∠AEC,
又 AE公共,
∴当∠B=∠C时,△ABE≌△ACE(AAS);
或BE=CE时,△ABE≌△ACE(SAS);
或∠BAE=∠CAE时,△ABE≌△ACE(ASA).
三、解答题(本大题共8小题,共56分)
17.(6分)计算:(﹣)﹣1﹣2+(π﹣3.14)0.
【分析】根据负整数指数幂以及零指数幂的运算法则分别进行计算,即可得出答案.
【解答】解:(﹣)﹣1﹣2+(π﹣3.14)0
=﹣2﹣2+1
=﹣4+1
=﹣3.
18.(6分)解方程:.
【分析】观察可得2﹣x=﹣(x﹣2),所以可确定方程最简公分母为:(x﹣2),然后去分母将分式方程化成整式方程求解.注意检验.
【解答】解:方程两边同乘以(x﹣2),
得:x﹣3+(x﹣2)=﹣3,
解得x=1,
检验:x=1时,x﹣2≠0,
∴x=1是原分式方程的解.
19.(8分)先化简,再求值:.选一个你所喜欢的数代入求值.
【分析】原式第一项利用除法法则变形,约分后利用同分母分式的减法法则计算得到最简结果,把a=0代入计算即可求出值.
【解答】解:原式= ﹣=﹣=﹣,
当a=0时,原式=﹣.
20.(8分)观察下面的变形规律:
=1﹣;=﹣;=﹣;……解答下面的问题:
(1)若n为正整数,请你猜想= .
(2)若n为正整数,请你用所学的知识证明﹣=.
(3)求和:+++…+.
【分析】(1)根据所给的等式进行分析,不难得出结果;
(2)把等式的左边进行运算,即可得出结果;
(3)结合(1)中的规律进行求解即可.
【解答】解:(1)∵=1﹣;
=﹣;
=﹣;
…,
∴=,
故答案为:;
(2)﹣
=
=,
∴﹣=;
(3)+++…+
=1﹣+++…+
=1﹣
=.
21.(8分)如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,求AC的长.
【分析】根据线段垂直平分线的性质和三角形的周长公式即可得到结论.
【解答】解:∵DE是边AB的垂直平分线,
∴AE=BE.
∴△BCE的周长=BC+BE+CE=BC+AE+CE=BC+AC=18cm.
又∵BC=8cm,
∴AC=10(cm).
22.(8分)如图,D、E在BC上,且BD=CE,AD=AE,∠ADE=∠AED,求证:AB=AC.
【分析】先求出BE=CD,再利用“边角边”证明△ABE和△ACD全等,根据全等三角形对应边相等证明即可.
【解答】证明:∵BD=CE,
∴BD+DE=CE+DE,
即BE=CD,
在△ABE和△ACD中,,
∴△ABE≌△ACD(SAS),
∴AB=AC.
23.(10分)为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买A种图书花费了3000元,购买B种图书花费了1600元,A种图书的单价是B种图书的1.5倍,购买A种图书的数量比B种图书多20本.
(1)求A和B两种图书的单价;
(2)书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了A种图书20本和B种图书25本,共花费多少元?
【分析】(1)设B种图书的单价为x元,则A种图书的单价为1.5x元,根据数量=总价÷单价结合花3000元购买的A种图书比花1600元购买的B种图书多20本,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)根据总价=单价×数量,即可求出结论.
【解答】解:(1)设B种图书的单价为x元,则A种图书的单价为1.5x元,
依题意,得:﹣=20,
解得:x=20,
经检验,x=20是所列分式方程的解,且符合题意,
∴1.5x=30.
答:A种图书的单价为30元,B种图书的单价为20元.
(2)30×0.8×20+20×0.8×25=880(元).
答:共花费880元.
24.(10分)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
【分析】(1)由∠ACB=90°,得∠ACD+∠BCE=90°,而AD⊥MN于D,BE⊥MN于E,则∠ADC=∠CEB=90°,根据等角的余角相等得到∠ACD=∠CBE,易得Rt△ADC≌Rt△CEB,所以AD=CE,DC=BE,即可得到DE=DC+CE=BE+AD.
(2)根据等角的余角相等得到∠ACD=∠CBE,易得△ADC≌△CEB,得到AD=CE,DC=BE,所以DE=CE﹣CD=AD﹣BE.
(3)DE、AD、BE具有的等量关系为:DE=BE﹣AD.证明的方法与(2)相同.
【解答】(1)证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
而AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE.
在△ADC和△CEB中,,
∴△ADC≌△CEB,
∴AD=CE,DC=BE,
∴DE=DC+CE=BE+AD;
(2)证明:在△ADC和△CEB中,,
∴△ADC≌△CEB,
∴AD=CE,DC=BE,
∴DE=CE﹣CD=AD﹣BE;
(3)DE=BE﹣AD.
易证得△ADC≌△CEB,
∴AD=CE,DC=BE,
∴DE=CD﹣CE=BE﹣AD.
一、选择题(每小题有且只有一个正确答案,本题共8小题,每小题3分,共24分)
1.(3分)下列分式是最简分式的是( )
A. B.
C. D.
2.(3分)有下列命题:①两点之间,线段最短;②相等的角是对顶角;③当a≥0时,|a|=a;④内错角互补,两直线平行.其中是真命题的有( )
A.1个 B.2个 C.3个 D.4个
3.(3分)若分式的值为0,则x的值为( )
A.0 B.1 C.﹣1 D.±1
4.(3分)要使分式有意义,则x应满足的条件是( )
A.x≠1 B.x≠﹣1 C.x≠0 D.x>1
5.(3分)下列运算正确的是( )
A.(x3)2=x5 B.(﹣x)5=﹣x5
C.x3 x2=x6 D.3x2+2x3=5x5
6.(3分)某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
7.(3分)如图,△ABC≌△BAD,点A和点B,点C和点D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB度数是( )
A.80° B.70° C.60° D.50°
8.(3分)货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是( )
A. B. C. D.
二、填空题(本题共8小题,每小题4分,共24分)
9.(4分)计算:(a﹣2)3= .
10.(4分)计算:+= .
11.(4分)如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B= .
12.(4分)已知关于x的方程会产生增根,则k的值为 .
13.(4分)每年四月北京很多地方杨絮、柳絮如雪花般飞舞.据测定,杨絮纤维的直径约为0.0000105米,将0.0000105用科学记数法可表示为 .
14.(4分)等腰三角形的两边的长分别为5cm和7cm,则此三角形的周长是 .
15.(4分)在△ABC中,∠A=70°,∠A比∠B大10°,则∠C= °.
16.(4分)如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件是 (填上你认为适当的一个条件即可).
三、解答题(本大题共8小题,共56分)
17.(6分)计算:(﹣)﹣1﹣2+(π﹣3.14)0.
18.(6分)解方程:.
19.(8分)先化简,再求值:.选一个你所喜欢的数代入求值.
20.(8分)观察下面的变形规律:
=1﹣;=﹣;=﹣;……解答下面的问题:
(1)若n为正整数,请你猜想= .
(2)若n为正整数,请你用所学的知识证明﹣=.
(3)求和:+++…+.
21.(8分)如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,求AC的长.
22.(8分)如图,D、E在BC上,且BD=CE,AD=AE,∠ADE=∠AED,求证:AB=AC.
23.(10分)为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买A种图书花费了3000元,购买B种图书花费了1600元,A种图书的单价是B种图书的1.5倍,购买A种图书的数量比B种图书多20本.
(1)求A和B两种图书的单价;
(2)书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了A种图书20本和B种图书25本,共花费多少元?
24.(10分)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
2021-2022学年湖南省岳阳市汨罗市弼时片八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(每小题有且只有一个正确答案,本题共8小题,每小题3分,共24分)
1.(3分)下列分式是最简分式的是( )
A. B.
C. D.
【分析】利用最简分式定义:分子分母没有公因式的分式,判断即可.
【解答】解:A、原分式的分子分母中不含有公因式,故此选项符合题意;
B、原式=,故此选项不符合题意;
C、原式=,故此选项不符合题意;
D、原式=,故此选项不符合题意;
故选:A.
2.(3分)有下列命题:①两点之间,线段最短;②相等的角是对顶角;③当a≥0时,|a|=a;④内错角互补,两直线平行.其中是真命题的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据两点之间线段最短、对顶角的概念、绝对值的性质、平行线的判定定理判断即可.
【解答】解:①两点之间,线段最短,本说法是真命题;
②相等的角不一定是对顶角,本小题说法是假命题;
③当a≥0时,|a|=a,本说法是真命题;
④内错角相等,两直线平行,本小题说法是假命题;
故选:B.
3.(3分)若分式的值为0,则x的值为( )
A.0 B.1 C.﹣1 D.±1
【分析】根据分式为0的条件列出关于x的不等式组,求出x的值即可.
【解答】解:∵分式的值为零,
∴,解得x=1.
故选:B.
4.(3分)要使分式有意义,则x应满足的条件是( )
A.x≠1 B.x≠﹣1 C.x≠0 D.x>1
【分析】本题主要考查分式有意义的条件:分母不能为0.
【解答】解:∵x+1≠0,
∴x≠﹣1.
故选:B.
5.(3分)下列运算正确的是( )
A.(x3)2=x5 B.(﹣x)5=﹣x5
C.x3 x2=x6 D.3x2+2x3=5x5
【分析】根据幂的乘方,同底数幂的乘法以及合并同类项计算法则进行解答.
【解答】解:A、原式=x6,故本选项错误;
B、原式=﹣x5,故本选项正确;
C、原式=x5,故本选项错误;
D、3x2与2x3不是同类项,不能合并,故本选项错误;
故选:B.
6.(3分)某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
【分析】本题就是已知三角形破损部分的边角,得到原来三角形的边角,根据三角形全等的判定方法,即可求解.
【解答】解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;
第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去.
故选:C.
7.(3分)如图,△ABC≌△BAD,点A和点B,点C和点D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB度数是( )
A.80° B.70° C.60° D.50°
【分析】根据全等三角形的性质得到∠DBA=∠CAB=50°,根据三角形内角和定理计算即可.
【解答】解:△ABC≌△BAD,点A和点B,点C和点D是对应点,
∴∠DBA=∠CAB=50°,
∴∠DAB=180°﹣70°﹣50°=60°,
故选:C.
8.(3分)货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是( )
A. B. C. D.
【分析】题中等量关系:货车行驶25千米与小车行驶35千米所用时间相同,列出关系式.
【解答】解:根据题意,得
.
故选:C.
二、填空题(本题共8小题,每小题4分,共24分)
9.(4分)计算:(a﹣2)3= a﹣6 .
【分析】根据负整数指数幂的运算法则进行计算即可.
【解答】解:(a﹣2)3=a﹣6.
故答案为:a﹣6.
10.(4分)计算:+= 0 .
【分析】原式变形后,利用同分母分式的减法法则计算即可得到结果.
【解答】解:原式=﹣=0,
故答案为:0
11.(4分)如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B= 70° .
【分析】根据三角形的外角等于与它不相邻的两个内角和,即可得出∠B的度数.
【解答】解:∵∠ACD=∠A+∠B,∠A=80°,∠ACD=150°,
∴∠B=70°.
故答案为:70°.
12.(4分)已知关于x的方程会产生增根,则k的值为 8 .
【分析】首先让最简公分母x﹣4=0,得到x=4,然后代入化为整式方程的方程,求出k的值是多少即可.
【解答】解:方程两边都乘(x﹣4),
可得:2x=k,
∵原方程有增根,
∴x﹣4=0,
解得x=4,
当x=4时,k=2×4=8.
故答案为:8.
13.(4分)每年四月北京很多地方杨絮、柳絮如雪花般飞舞.据测定,杨絮纤维的直径约为0.0000105米,将0.0000105用科学记数法可表示为 1.05×10﹣5 .
【分析】绝对值小于1的负数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.0000105=1.05×10﹣5.
故答案为:1.05×10﹣5.
14.(4分)等腰三角形的两边的长分别为5cm和7cm,则此三角形的周长是 17cm或19cm .
【分析】根据等腰三角形的性质,分两种情况:①当腰长为5cm时,②当腰长为7cm时,解答出即可.
【解答】解:根据题意,
①当腰长为5cm时,周长=5+5+7=17(cm);
②当腰长为7cm时,周长=5+7+7=19(cm);
故答案为:17cm或19cm.
15.(4分)在△ABC中,∠A=70°,∠A比∠B大10°,则∠C= 50 °.
【分析】由题意可得∠B=60°,利用三角形的内角和定理即可求∠C.
【解答】解:∵∠A=70°,∠A比∠B大10°,
∴∠B=∠A﹣10°=60°,
∴∠C=180°﹣∠A﹣∠B=50°.
故答案为:50.
16.(4分)如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件是 ∠B=∠C (填上你认为适当的一个条件即可).
【分析】根据题意,易得∠AEB=∠AEC,又AE公共,所以根据全等三角形的判定方法容易寻找添加条件.
【解答】解:∵∠1=∠2,∴∠AEB=∠AEC,
又 AE公共,
∴当∠B=∠C时,△ABE≌△ACE(AAS);
或BE=CE时,△ABE≌△ACE(SAS);
或∠BAE=∠CAE时,△ABE≌△ACE(ASA).
三、解答题(本大题共8小题,共56分)
17.(6分)计算:(﹣)﹣1﹣2+(π﹣3.14)0.
【分析】根据负整数指数幂以及零指数幂的运算法则分别进行计算,即可得出答案.
【解答】解:(﹣)﹣1﹣2+(π﹣3.14)0
=﹣2﹣2+1
=﹣4+1
=﹣3.
18.(6分)解方程:.
【分析】观察可得2﹣x=﹣(x﹣2),所以可确定方程最简公分母为:(x﹣2),然后去分母将分式方程化成整式方程求解.注意检验.
【解答】解:方程两边同乘以(x﹣2),
得:x﹣3+(x﹣2)=﹣3,
解得x=1,
检验:x=1时,x﹣2≠0,
∴x=1是原分式方程的解.
19.(8分)先化简,再求值:.选一个你所喜欢的数代入求值.
【分析】原式第一项利用除法法则变形,约分后利用同分母分式的减法法则计算得到最简结果,把a=0代入计算即可求出值.
【解答】解:原式= ﹣=﹣=﹣,
当a=0时,原式=﹣.
20.(8分)观察下面的变形规律:
=1﹣;=﹣;=﹣;……解答下面的问题:
(1)若n为正整数,请你猜想= .
(2)若n为正整数,请你用所学的知识证明﹣=.
(3)求和:+++…+.
【分析】(1)根据所给的等式进行分析,不难得出结果;
(2)把等式的左边进行运算,即可得出结果;
(3)结合(1)中的规律进行求解即可.
【解答】解:(1)∵=1﹣;
=﹣;
=﹣;
…,
∴=,
故答案为:;
(2)﹣
=
=,
∴﹣=;
(3)+++…+
=1﹣+++…+
=1﹣
=.
21.(8分)如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,求AC的长.
【分析】根据线段垂直平分线的性质和三角形的周长公式即可得到结论.
【解答】解:∵DE是边AB的垂直平分线,
∴AE=BE.
∴△BCE的周长=BC+BE+CE=BC+AE+CE=BC+AC=18cm.
又∵BC=8cm,
∴AC=10(cm).
22.(8分)如图,D、E在BC上,且BD=CE,AD=AE,∠ADE=∠AED,求证:AB=AC.
【分析】先求出BE=CD,再利用“边角边”证明△ABE和△ACD全等,根据全等三角形对应边相等证明即可.
【解答】证明:∵BD=CE,
∴BD+DE=CE+DE,
即BE=CD,
在△ABE和△ACD中,,
∴△ABE≌△ACD(SAS),
∴AB=AC.
23.(10分)为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买A种图书花费了3000元,购买B种图书花费了1600元,A种图书的单价是B种图书的1.5倍,购买A种图书的数量比B种图书多20本.
(1)求A和B两种图书的单价;
(2)书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了A种图书20本和B种图书25本,共花费多少元?
【分析】(1)设B种图书的单价为x元,则A种图书的单价为1.5x元,根据数量=总价÷单价结合花3000元购买的A种图书比花1600元购买的B种图书多20本,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)根据总价=单价×数量,即可求出结论.
【解答】解:(1)设B种图书的单价为x元,则A种图书的单价为1.5x元,
依题意,得:﹣=20,
解得:x=20,
经检验,x=20是所列分式方程的解,且符合题意,
∴1.5x=30.
答:A种图书的单价为30元,B种图书的单价为20元.
(2)30×0.8×20+20×0.8×25=880(元).
答:共花费880元.
24.(10分)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
【分析】(1)由∠ACB=90°,得∠ACD+∠BCE=90°,而AD⊥MN于D,BE⊥MN于E,则∠ADC=∠CEB=90°,根据等角的余角相等得到∠ACD=∠CBE,易得Rt△ADC≌Rt△CEB,所以AD=CE,DC=BE,即可得到DE=DC+CE=BE+AD.
(2)根据等角的余角相等得到∠ACD=∠CBE,易得△ADC≌△CEB,得到AD=CE,DC=BE,所以DE=CE﹣CD=AD﹣BE.
(3)DE、AD、BE具有的等量关系为:DE=BE﹣AD.证明的方法与(2)相同.
【解答】(1)证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
而AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE.
在△ADC和△CEB中,,
∴△ADC≌△CEB,
∴AD=CE,DC=BE,
∴DE=DC+CE=BE+AD;
(2)证明:在△ADC和△CEB中,,
∴△ADC≌△CEB,
∴AD=CE,DC=BE,
∴DE=CE﹣CD=AD﹣BE;
(3)DE=BE﹣AD.
易证得△ADC≌△CEB,
∴AD=CE,DC=BE,
∴DE=CD﹣CE=BE﹣AD.
同课章节目录
