2021-2022学年北师大版九年级数学下册1.6利用三角函数测高 解答专题训练 (Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册1.6利用三角函数测高 解答专题训练 (Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 466.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 08:32:45 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《1.6利用三角函数测高》解答专题训练(附答案)
1.近几年,我国国家海洋局高度重视海上巡逻.如图,上午9时,巡逻船位于A处,观测到某港口城市P位于巡逻船的北偏西67.5°,巡逻船以21海里/时的速度向正北方向行驶,下午2时巡逻船到达B处,这时观测到城市P位于巡逻船的南偏西36.9°方向,求此时巡逻船所在B处与城市P的距离?(参考数据:sin36.9°≈,tan36.9°≈,sin67.5°≈,tan67.5°≈)
2.南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向东南方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后在C处成功拦截不明船只,问我国海监执法船在前往监视巡查的过程中行驶了多少海里?
3.王亮同学要测量广场内被湖水隔开的两颗大树A和B之间的距离,它在A处测得B在A的北偏西30°方向,他从A处出发向北偏东15°方向走了200米到达C处,这时测得大树B在C的北偏西60°的方向.
(1)求∠ABC的度数;
(2)求两颗大树A和B之间的距离(结果精确到1米)(参考数据:≈1.414,,1.732,≈2.449)
4.超速行驶是一种十分危险的违法驾驶行为,在一条东西走向的笔直高速公路MN上,小型车限速为每小时100千米.现有一辆小汽车行驶到A处时,发现北偏东30°方向200米处有一超速监测仪P10秒后,小汽车行驶至B处,测得监测仪P在B处的北偏西45°方向上.请问:这辆车超速了吗?通过计算说明理由.(参考数据:≈1.41,≈1.73)
5.某条道路上通行车辆的限速60千米/时,道路的AB段为监测区,监测点P到AB的距离PH为50米(如图).已知点P在点A的北偏东45°方向上,且在点B的北偏西60°方向上,点B在点A的北偏东75°方向上,那么车辆通过AB段的时间在多少秒以内,可认定为超速?(参考数据:≈1.7,≈1.4).
6.如图,一艘海轮位于小岛C的南偏东60°方向,距离小岛120海里的A处,该海轮从A处正北方向航行一段距离后,到达位于小岛C北偏东45°方向的B处.
(1)求该海轮从A处到B处的航行过程中与小岛C之间的最短距离(记过保留根号);
(2)如果该海轮以每小时20海里的速度从B处沿BC方向行驶,求它从B处到达小岛C的航行时间(结果精确到0.1小时).(参考数据:=1.41,=1.73)
7.码头A、B位于东西走向的河岸线l上,一游轮在P处测得码头A在其北偏东70°,游轮向东航行10分钟后到达Q处,此时测得码头B在其北偏东35°.已知游轮的速度为30千米/小时,两码头A、B相距2千米.
(1)求点P到河岸线l的距离;
(2)若该游轮按原速度从点Q驶向码头B,则至少需要多长时间才能到达码头B?(sin35°≈,cos35°≈,tan35°≈,sin70°≈,cos70°≈,tan70°≈)
8.如图,在一笔直的海岸线上有A,B两个观测站,A观测站在B观测站的正东方向,有一艘小船在点P处,从A处测得小船在北偏西60°方向,从B处测得小船在北偏东45°的方向,点P到点B的距离是3千米.(注:结果有根号的保留根号)
(1)求A,B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向以千米/时的速度进行沿途考察,航行一段时间后到达点C处,此时,从B测得小船在北偏西15°方向,求小船沿途考察的时间.
9.周末小明和同学们去“绿博园”的枫湖坐船,观赏风景;如图,小明正在A处的小船上,B处小船上的游客发现点A在点B的正西方向上,C处小船上的游客发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120米.
(1)求出此时点A到点C的距离
(2)若小明从A处沿AC方向向C驶去,当到达点Aˊ时,测得点B在Aˊ的南偏东75°的方向上,求此时小明所乘坐的小船走的距离.(注:结果保留根号)
10.如图,自来水厂A和村庄B在小河1的两侧,现要在A,B间铺设一条输水管道,为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏西49°方向,B位于南偏西41°方向.
(1)求BQ长度;
(2)求A,B间的距离.(参考数据:cos41°≈0.75)
11.由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴的侵袭.近日,A城气象局测得沙尘暴中心在A城的正北方向240km的B处,以12km/h的速度向南偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域.
(1)A城是否受到这次沙尘暴的影响,为什么?
(2)若A城受这次沙尘暴影响,那么遭受影响的时间有多长?
12.如图,海面上甲、乙两船分别从A,B两处同时出发,由西向东行驶,甲船的速度为24nmile/h,乙船的速度为15nmile/h,出发时,测得乙船在甲船北偏东50°方向,且AB=10nmile,经过20分钟后,甲、乙两船分别到达C,D两处.
(参考值:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
(1)求两条航线间的距离;
(2)若两船保持原来的速度和航向,还需要多少时间才能使两船的距离最短?(精确到0.01)
13.向阳中学校园内有一条林萌道叫“勤学路”,道路两边有如图所示的路灯(在铅垂面内的示意图),灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
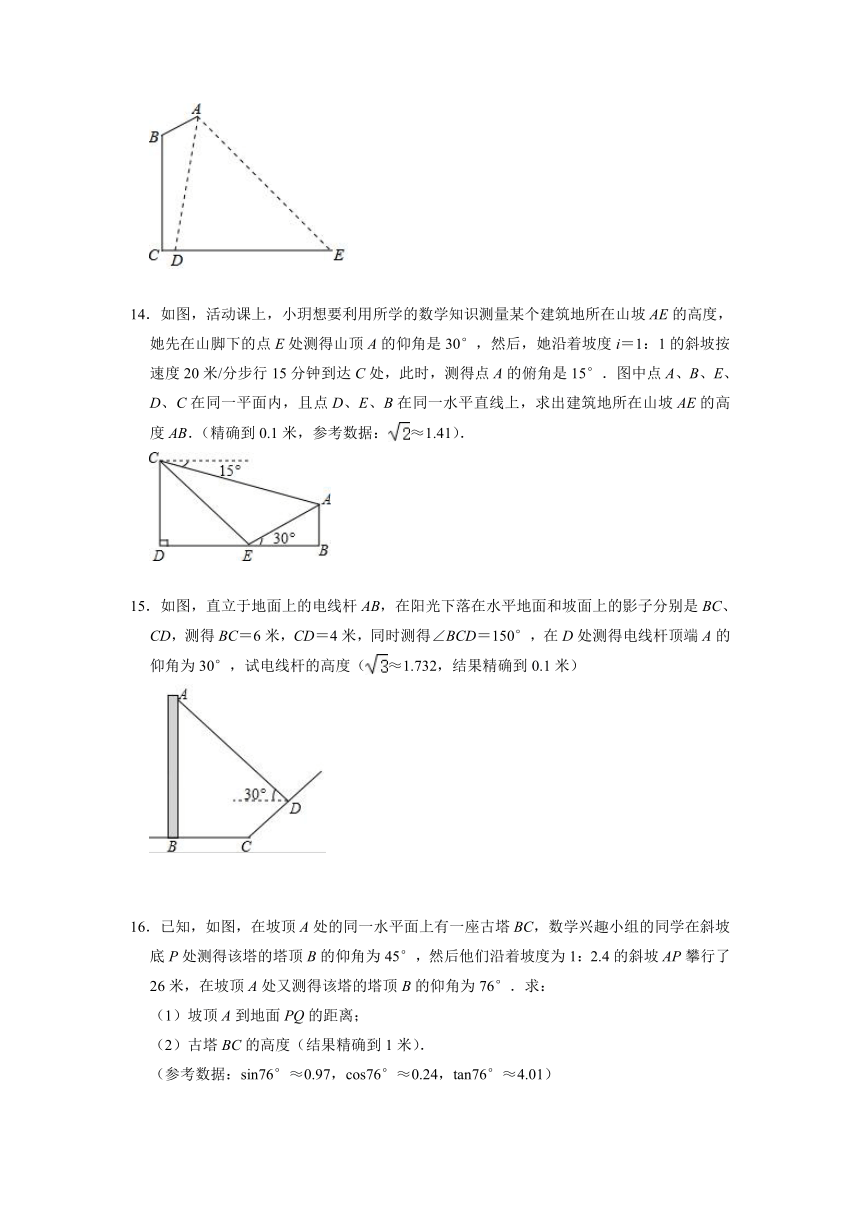
14.如图,活动课上,小玥想要利用所学的数学知识测量某个建筑地所在山坡AE的高度,她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1:1的斜坡按速度20米/分步行15分钟到达C处,此时,测得点A的俯角是15°.图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出建筑地所在山坡AE的高度AB.(精确到0.1米,参考数据:≈1.41).
15.如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,同时测得∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试电线杆的高度(≈1.732,结果精确到0.1米)
16.已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求:
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
17.如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,测得B,C两点的俯角分别为60°和45°,已知热气球离地面的高度为120m,且大桥与地面在同一水平面上,求大桥BC的长度(结果保留整数,≈1.72).
18.如图,小明所在教学楼的每层高度为3.6米,为了测量旗杆MN的高度,他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°,他在二楼窗台B处测得M的仰角为30°,已知每层楼的窗台离该层的地面高度均为1米,求旗杆MN的高度
(结果保留根号).
19.让每一个孩子在家门口就能“上好学”,合肥某中学依山而建.校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=45°,离B点A(3﹣)米远的E处有一花台,在E处仰望C的仰角∠CEF=60°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i.
(2)求DC的长.
20.如图,从坡上建筑物AB观测坡地建筑物CD,从A点处测得C点的俯角为45°,从B点处测得D点的俯角为30°,已知建筑物AB的高度为10m,AB与CD的水平距离是OD=15m,求CD的高度.
21.如图,学校数学兴趣小组在大运河的斜坡AB上,要测量河对岸镇国寺塔MN的高度,他们在斜坡AB上的C处,测得镇国寺塔MN的顶端N的仰角是20°,沿斜坡AB走10米,到达坡底B处(B处于镇国寺塔MN的底端M在同一水平线上),在B处测得镇国寺塔MN顶端N的仰角是30°,若斜坡AB的坡比为3:4,求镇国寺塔MN的高度.(结果保留整数,参考数据:sin20°≈0.3,cos20°≈0.9,tan20°≈0.4,≈1.7)
参考答案
1.解:过点P作PC⊥AB,垂足为C,设PC=x海里.
在Rt△APC中,∵tan∠A=,
∴AC=,
在Rt△PCB中,∵tan∠B=,
∴BC=,
∵AC+BC=AB=21×5,
∴,解得x=60,
∵,
∴(海里).
∴巡逻船所在B处与城市P的距离为100海里.
2.解:过B作BD⊥AC,
∵∠BAC=75°﹣30°=45°,
∴在Rt△ABD中,∠BAD=∠ABD=45°,∠ADB=90°,
由勾股定理得:BD=AD=×20=10(海里),
在Rt△BCD中,∠C=60°,∠CBD=30°,
∴tan∠CBD=,即CD=10×=,
则AC=AD+DC=10+(海里),即我海监执法船在前往监视巡查的过程中行驶了10+海里.
3.解:由题意可知:∠BAC=∠BAD+∠CAD=30°+15°=45°,
∠MCA=∠CAD=15°,
∴∠ACB=180°﹣∠MCA﹣∠BCN=180°﹣15°﹣60°=105°,
在△ABC中,
∠ABC=180°﹣∠BCA﹣∠BAC=180°﹣105°﹣45°=30°;
过点C作CH⊥AB于点H,
在Rt△ACH中,∵AC=200(米),∠CAH=45°,
∴CH=ACsin∠CAH=200×sin45°=200×=100(米)
∴AH=CH=100 (米)
在Rt△BCH中,∵CH=100 (米),∠CBH=30°,
∴;
∴AB=AH+BH=100+100≈386(米)
答:两棵大树A和B之间的距离约为386米.
4.解:这辆车没有超速.理由如下:
过点P作PC⊥AB于C,则∠PCA=∠PCB=90°.
由题可知:∠APC=30°,∠BPC=45°,
∴在Rt△APC中,AC=PA=×200=100(米),PC=AC=100米.
在Rt△BCP中,BC=PC=100米,
∴AB=AC+BC=100+100(米),
∵行驶时间为10秒,
∴这辆车的速度为=10+10≈27.3(米/秒),
100千米/时≈27.8米/秒,
27.3米/秒<27.8米/秒,
所以,这辆车没有超速,
5.解:如图,由题意知∠CAB=75°、∠CAP=45°、∠PBD=60°,
∴∠PAH=∠CAB﹣∠CAP=30°,
∵∠PHA=∠PHB=90°,PH=50,
∴AH===50,
∵AC∥BD,
∴∠ABD=180°﹣∠CAB=105°,
∴∠PBH=∠ABD﹣∠PBD=45°,
则PH=BH=50,
∴AB=AH+BH=50+50,
∵60千米/时=米/秒,
∴时间t==3+3≈8.1(秒),
即车辆通过AB段的时间在8.1秒以内,可认定为超速.
6.解:(1)如图,过点C作CD⊥AB于D,
由题意,得∠ACD=30°.
在直角△ACD中,∠ADC=90°,
∴cos∠ACD=,
∴CD=AC cos30°=120×=60(海里);
(2)在直角△BCD中,∠BDC=90°,∠DCA=45°,
∴cos∠BCD=,
∴BC===60≈60×2.44=146.4(海里),
∴146.4÷20=7.32≈7.3(小时).
答:(1)求该海轮从A处到B处的航行过程中与小岛C之间的最短距离是60海里;
(2)如果该海轮以每小时20海里的速度从B处沿BC方向行驶,求它从B处到达小岛C的航行时间约为7.3小时.
7.解:(1)过点B作BE⊥PQ于E,作BF∥AP交PQ于点F.
∵AB∥PQ,BF∥AP,
∴四边形APFB是平行四边形,
∴PF=AB=2千米,∠EFB=∠EPA=20°,
∴FQ=PQ﹣PF=30×﹣2=3(千米).
在△BFQ中,∵∠BFQ=20°,∠FQB=90°+35°=125°,
∴∠FBQ=180°﹣∠BFQ﹣∠FQB=35°,
设BE=x,FQ=FE﹣QE,FE=x tan70°,QE=35×tan35°,
可得x tan70°﹣35×tan35°=3,
解得x=.
答:点P到河岸线l的距离是千米;
(2)∵BQ=千米,游轮的速度为30千米/小时,
∴该游轮按原速度从点Q驶向码头B的时间为:÷30=(小时).
答:若该游轮按原速度从点Q驶向码头B,则它至少需要小时才能到达码头B.
8.解:(1)如图,过点P作PD⊥AB于点D.
在Rt△PBD中,∠BDP=90°,∠PBD=90°﹣45°=45°,
∴BD=PD=3千米.
在Rt△PAD中,∠ADP=90°,∠PAD=90°﹣60°=30°,
∴AD=PD=3千米,PA=6千米.
∴AB=BD+AD=3+3(千米);
(2)如图,过点B作BF⊥AC于点F.
根据题意得:∠ABC=105°,
在Rt△ABF中,∠AFB=90°,∠BAF=30°,
∴BF=AB=千米,AF=AB= 千米.
在△ABC中,∠C=180°﹣∠BAC﹣∠ABC=45°.
在Rt△BCF中,∠BFC=90°,∠C=45°,
∴CF=BF=千米,
∴PC=AF+CF﹣AP=3千米.
故小船沿途考察的时间为:3÷=3(小时).
9.解:(1)作CD⊥BA交BA的延长线于点D,
由题意可得,BC=120米,∠CBD=30°,
则CD=60米,
∵∠DCA=30°,
∴AC=米,
即此时点A到点C的距离是40米;
(2)作A′N⊥BC于点N,作A′E⊥BA交BA的延长线于点E,
由题意可得,
∠1=30°,∠EA′B=′75°,∠EA′A=30°,∠CBD=30°,
则∠AA′B=45°,
∴∠2=15°,
∴∠A′BE=15°,
∴A′N=A′E,
设AA′=x,
则A′E=,
∴A′N=,
∴CA′=,
∵CA=,
∴x+x=40,
得x=60﹣20,
答:此时小明所乘坐的小船走的距离是(60﹣20)米.
10.解:(1)∵B位于P点南偏东24.5°方向,
∴∠BPQ=90°﹣24.5°=65.5°,
又∵B位于Q点南偏西41°方向,
∴∠PQB=90°﹣41°=49°,
∴∠PBQ=180°﹣65.5°﹣49°=65.5°,即∠PBQ=∠BPQ,
∴BQ=PQ=1200(m);
(2)∵点P处测得A在正北方向,
∴∠APQ=90°.在Rt△APQ中,cos∠AQP≈0.75
∴AQ=1200÷0.75=1600,
∵在点Q处,测得A位于北偏西49°方向,B位于南偏西41°方向,
∴∠AQB=90°,在Rt△ABQ中,
AB===2000(m)
答:A,B间的距离约为2000m.
11.解:(1)过点A作AD⊥BC,垂足为D,
在Rt△ABD中,由题意可知∠DBA=30°,
∴AD=AB=×240=120(km),
∵AD=120<150,
∴A城将受这次沙尘暴的影响;
(2)设点E,F是以A为圆心,150km为半径的圆与CB的交点,连接AE,AF,
由题意得DE==90(km),
∴EF=2DE=2×90=180(km),
∴A城受沙尘暴影响的时间为:180÷12=15(时),
答:A城将受到这次沙尘暴的影响,影响的时间为15时.
12.解:(1)过点A作AE⊥DB,交DB的延长线于E,
在Rt△AEB中,∵∠AEB=90°,∠EAB=50°,AB=10,
∴AE=AB cos50°=10×0.643=6.43(nmile),
答:两条航线间的距离为6.43(nmile);
(2)当甲乙两船的位置垂直时,两船之间的距离最短,过C作CF⊥BD于F.
∵BE=AB sin50°=7.66,
AC=24×=8,BD=15×=5,
∴DF=BD+BE﹣AC=4.66,
设还需要t小时才能使两船的距离最短,
则有:24t﹣15t=4.66,
解得t=0.52(h),
答:还需要0.52h才能使两船的距离最短.
13.解:过点A作AF⊥CE,交CE于点F,过点B作BG⊥AF,交AF于点G,则FG=BC=10.
由题意得∠ADE=α,∠E=45°.
设AF=x.
∵∠E=45°,
∴EF=AF=x.
在Rt△ADF中,∵tan∠ADF=,
∴DF==,
∵DE=13.3,
∴x+=13.3.
∴x=11.4.
∴AG=AF﹣GF=11.4﹣10=1.4.
∵∠ABC=120°,
∴∠ABG=∠ABC﹣∠CBG=120°﹣90°=30°.
∴AB=2AG=2.8,
答:灯杆AB的长度为2.8米.
14.解:作EF⊥AC于点F,
根据题意,CE=20×15=300米,
∵i=1:1,
∴tan∠CED=1,
∴∠CED=∠DCE=45°,
∵∠ECF=90°﹣45°﹣15°=30°,
∴EF=CE=150米,
∵∠CEF=60°,∠AEB=30°,
∴∠AEF=180°﹣45°﹣60°﹣30°=45°,
∴AF=EF=150米,
∴AE=(米),
∴AB=×150≈105.8(米).
答:建筑地所在山坡AE的高度AB约为105.8米.
15.解:延长AD交BC的延长线于E,作DF⊥BE于F,
∵∠BCD=150°,
∴∠DCF=30°,又CD=4m,
∴DF=2m,CF==2(m),
由题意得∠E=30°,
∴EF==2,
∴BE=BC+CF+EF=(6+4)m,
∴AB=BE×tanE=(6+4)×=2+4≈7.5(米),
答:电线杆的高度为7.5米.
16.解:(1)过点A作AH⊥PO,垂足为点H,
∵斜坡AP的坡度为1:2.4,
∴,
设AH=5k,则PH=12k,由勾股定理,得AP=13k,
∴13k=26,
解得k=2,
∴AH=10,
答:坡顶A到地面PQ的距离为10米.
(2)延长BC交PO于点D,
∵BC⊥AC,AC∥PO,
∴BD⊥PO,
∴四边形AHDC是矩形,CD=AH=10,AC=DH,
∵∠BPD=45°,
∴PD=BD,
设BC=x,则x+10=24+DH,
∴AC=DH=x﹣14,
在Rt△ABC中,tan76°=,即≈4.01.
解得x≈19.
答:古塔BC的高度约为19米.
17.解:作AD⊥CB交CB所在直线于点D.
由题知,∠ACD=45°,∠ABD=60°.
在Rt△ACD中,∠ACD=45°,
所以CD=AD=120 m.
在Rt△ABD中,∠ABD=60°,tan60°==,
所以BD=AD=,
所以BC=CD﹣BD=120﹣≈120﹣69.2≈51(m).
答:大桥BC的长度约为51m.
18.解:过点M的水平线交直线AB于点H,
由题意,得∠AMH=∠MAH=45°,∠BMH=30°,AB=3.6,
设MH=x,则AH=x,BH=xtan30°=x,
∴AB=AH﹣BH=x﹣x=3.6,
解得x=,
则旗杆高度MN=x+1=(米)
答:旗杆MN的高度度约为米.
19.解:(1)过B作BG⊥AD于G,
则四边形BGDF是矩形,
∴BG=DF=5米,
∵AB=13米,
∴AG==12米,
∴AB的坡度i==1:2.4;
(2)∵在Rt△BCF中,∠CBF=45°,
∴BF=CF,
∵在Rt△CEF中,∠CEF=60°,
∴EF=CF,
∵BE=4(3﹣)米,
∴BF﹣EF=CF﹣CF=4(3﹣),
解得:CF=12.
∴DC=CF+DF=12+5=17米.
20.解:作CE⊥AO于点E,如右图所示,
∵CE⊥AO,∠FAC=45°,OD=15m,
∴∠CAE=45°,CE=15m,
∴AE=15m,
∵AB=10m
∴BE=5m,
∵∠BOD=90°,∠BDO=30°,OD=15m,
∴BO=15×tan30°=15×=5m,
∴EO=BO﹣BE=5﹣5,
∴CD=EO=5﹣5.
21.解:如图作CH⊥MN于H,CK⊥BM于K.则四边形CHMK是矩形,设MN=a.
在Rt△MNB中,BM=a,
在Rt△BCK中,Ck:BK=3:4,设CK=3k,BK=4k,
∵(3k)2+(4k)2=102,
∴k=2(负根已经舍弃),
∴CK=HM=6,BK=8,KM=CH=8+a,
在Rt△CNH中,tan20°=,
∴=0.4,
解得a≈30(米),
答:镇国寺塔MN的高度为30米.
1.近几年,我国国家海洋局高度重视海上巡逻.如图,上午9时,巡逻船位于A处,观测到某港口城市P位于巡逻船的北偏西67.5°,巡逻船以21海里/时的速度向正北方向行驶,下午2时巡逻船到达B处,这时观测到城市P位于巡逻船的南偏西36.9°方向,求此时巡逻船所在B处与城市P的距离?(参考数据:sin36.9°≈,tan36.9°≈,sin67.5°≈,tan67.5°≈)
2.南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向东南方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后在C处成功拦截不明船只,问我国海监执法船在前往监视巡查的过程中行驶了多少海里?
3.王亮同学要测量广场内被湖水隔开的两颗大树A和B之间的距离,它在A处测得B在A的北偏西30°方向,他从A处出发向北偏东15°方向走了200米到达C处,这时测得大树B在C的北偏西60°的方向.
(1)求∠ABC的度数;
(2)求两颗大树A和B之间的距离(结果精确到1米)(参考数据:≈1.414,,1.732,≈2.449)
4.超速行驶是一种十分危险的违法驾驶行为,在一条东西走向的笔直高速公路MN上,小型车限速为每小时100千米.现有一辆小汽车行驶到A处时,发现北偏东30°方向200米处有一超速监测仪P10秒后,小汽车行驶至B处,测得监测仪P在B处的北偏西45°方向上.请问:这辆车超速了吗?通过计算说明理由.(参考数据:≈1.41,≈1.73)
5.某条道路上通行车辆的限速60千米/时,道路的AB段为监测区,监测点P到AB的距离PH为50米(如图).已知点P在点A的北偏东45°方向上,且在点B的北偏西60°方向上,点B在点A的北偏东75°方向上,那么车辆通过AB段的时间在多少秒以内,可认定为超速?(参考数据:≈1.7,≈1.4).
6.如图,一艘海轮位于小岛C的南偏东60°方向,距离小岛120海里的A处,该海轮从A处正北方向航行一段距离后,到达位于小岛C北偏东45°方向的B处.
(1)求该海轮从A处到B处的航行过程中与小岛C之间的最短距离(记过保留根号);
(2)如果该海轮以每小时20海里的速度从B处沿BC方向行驶,求它从B处到达小岛C的航行时间(结果精确到0.1小时).(参考数据:=1.41,=1.73)
7.码头A、B位于东西走向的河岸线l上,一游轮在P处测得码头A在其北偏东70°,游轮向东航行10分钟后到达Q处,此时测得码头B在其北偏东35°.已知游轮的速度为30千米/小时,两码头A、B相距2千米.
(1)求点P到河岸线l的距离;
(2)若该游轮按原速度从点Q驶向码头B,则至少需要多长时间才能到达码头B?(sin35°≈,cos35°≈,tan35°≈,sin70°≈,cos70°≈,tan70°≈)
8.如图,在一笔直的海岸线上有A,B两个观测站,A观测站在B观测站的正东方向,有一艘小船在点P处,从A处测得小船在北偏西60°方向,从B处测得小船在北偏东45°的方向,点P到点B的距离是3千米.(注:结果有根号的保留根号)
(1)求A,B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向以千米/时的速度进行沿途考察,航行一段时间后到达点C处,此时,从B测得小船在北偏西15°方向,求小船沿途考察的时间.
9.周末小明和同学们去“绿博园”的枫湖坐船,观赏风景;如图,小明正在A处的小船上,B处小船上的游客发现点A在点B的正西方向上,C处小船上的游客发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120米.
(1)求出此时点A到点C的距离
(2)若小明从A处沿AC方向向C驶去,当到达点Aˊ时,测得点B在Aˊ的南偏东75°的方向上,求此时小明所乘坐的小船走的距离.(注:结果保留根号)
10.如图,自来水厂A和村庄B在小河1的两侧,现要在A,B间铺设一条输水管道,为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏西49°方向,B位于南偏西41°方向.
(1)求BQ长度;
(2)求A,B间的距离.(参考数据:cos41°≈0.75)
11.由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴的侵袭.近日,A城气象局测得沙尘暴中心在A城的正北方向240km的B处,以12km/h的速度向南偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域.
(1)A城是否受到这次沙尘暴的影响,为什么?
(2)若A城受这次沙尘暴影响,那么遭受影响的时间有多长?
12.如图,海面上甲、乙两船分别从A,B两处同时出发,由西向东行驶,甲船的速度为24nmile/h,乙船的速度为15nmile/h,出发时,测得乙船在甲船北偏东50°方向,且AB=10nmile,经过20分钟后,甲、乙两船分别到达C,D两处.
(参考值:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
(1)求两条航线间的距离;
(2)若两船保持原来的速度和航向,还需要多少时间才能使两船的距离最短?(精确到0.01)
13.向阳中学校园内有一条林萌道叫“勤学路”,道路两边有如图所示的路灯(在铅垂面内的示意图),灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
14.如图,活动课上,小玥想要利用所学的数学知识测量某个建筑地所在山坡AE的高度,她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1:1的斜坡按速度20米/分步行15分钟到达C处,此时,测得点A的俯角是15°.图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出建筑地所在山坡AE的高度AB.(精确到0.1米,参考数据:≈1.41).
15.如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,同时测得∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试电线杆的高度(≈1.732,结果精确到0.1米)
16.已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求:
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
17.如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,测得B,C两点的俯角分别为60°和45°,已知热气球离地面的高度为120m,且大桥与地面在同一水平面上,求大桥BC的长度(结果保留整数,≈1.72).
18.如图,小明所在教学楼的每层高度为3.6米,为了测量旗杆MN的高度,他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°,他在二楼窗台B处测得M的仰角为30°,已知每层楼的窗台离该层的地面高度均为1米,求旗杆MN的高度
(结果保留根号).
19.让每一个孩子在家门口就能“上好学”,合肥某中学依山而建.校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=45°,离B点A(3﹣)米远的E处有一花台,在E处仰望C的仰角∠CEF=60°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i.
(2)求DC的长.
20.如图,从坡上建筑物AB观测坡地建筑物CD,从A点处测得C点的俯角为45°,从B点处测得D点的俯角为30°,已知建筑物AB的高度为10m,AB与CD的水平距离是OD=15m,求CD的高度.
21.如图,学校数学兴趣小组在大运河的斜坡AB上,要测量河对岸镇国寺塔MN的高度,他们在斜坡AB上的C处,测得镇国寺塔MN的顶端N的仰角是20°,沿斜坡AB走10米,到达坡底B处(B处于镇国寺塔MN的底端M在同一水平线上),在B处测得镇国寺塔MN顶端N的仰角是30°,若斜坡AB的坡比为3:4,求镇国寺塔MN的高度.(结果保留整数,参考数据:sin20°≈0.3,cos20°≈0.9,tan20°≈0.4,≈1.7)
参考答案
1.解:过点P作PC⊥AB,垂足为C,设PC=x海里.
在Rt△APC中,∵tan∠A=,
∴AC=,
在Rt△PCB中,∵tan∠B=,
∴BC=,
∵AC+BC=AB=21×5,
∴,解得x=60,
∵,
∴(海里).
∴巡逻船所在B处与城市P的距离为100海里.
2.解:过B作BD⊥AC,
∵∠BAC=75°﹣30°=45°,
∴在Rt△ABD中,∠BAD=∠ABD=45°,∠ADB=90°,
由勾股定理得:BD=AD=×20=10(海里),
在Rt△BCD中,∠C=60°,∠CBD=30°,
∴tan∠CBD=,即CD=10×=,
则AC=AD+DC=10+(海里),即我海监执法船在前往监视巡查的过程中行驶了10+海里.
3.解:由题意可知:∠BAC=∠BAD+∠CAD=30°+15°=45°,
∠MCA=∠CAD=15°,
∴∠ACB=180°﹣∠MCA﹣∠BCN=180°﹣15°﹣60°=105°,
在△ABC中,
∠ABC=180°﹣∠BCA﹣∠BAC=180°﹣105°﹣45°=30°;
过点C作CH⊥AB于点H,
在Rt△ACH中,∵AC=200(米),∠CAH=45°,
∴CH=ACsin∠CAH=200×sin45°=200×=100(米)
∴AH=CH=100 (米)
在Rt△BCH中,∵CH=100 (米),∠CBH=30°,
∴;
∴AB=AH+BH=100+100≈386(米)
答:两棵大树A和B之间的距离约为386米.
4.解:这辆车没有超速.理由如下:
过点P作PC⊥AB于C,则∠PCA=∠PCB=90°.
由题可知:∠APC=30°,∠BPC=45°,
∴在Rt△APC中,AC=PA=×200=100(米),PC=AC=100米.
在Rt△BCP中,BC=PC=100米,
∴AB=AC+BC=100+100(米),
∵行驶时间为10秒,
∴这辆车的速度为=10+10≈27.3(米/秒),
100千米/时≈27.8米/秒,
27.3米/秒<27.8米/秒,
所以,这辆车没有超速,
5.解:如图,由题意知∠CAB=75°、∠CAP=45°、∠PBD=60°,
∴∠PAH=∠CAB﹣∠CAP=30°,
∵∠PHA=∠PHB=90°,PH=50,
∴AH===50,
∵AC∥BD,
∴∠ABD=180°﹣∠CAB=105°,
∴∠PBH=∠ABD﹣∠PBD=45°,
则PH=BH=50,
∴AB=AH+BH=50+50,
∵60千米/时=米/秒,
∴时间t==3+3≈8.1(秒),
即车辆通过AB段的时间在8.1秒以内,可认定为超速.
6.解:(1)如图,过点C作CD⊥AB于D,
由题意,得∠ACD=30°.
在直角△ACD中,∠ADC=90°,
∴cos∠ACD=,
∴CD=AC cos30°=120×=60(海里);
(2)在直角△BCD中,∠BDC=90°,∠DCA=45°,
∴cos∠BCD=,
∴BC===60≈60×2.44=146.4(海里),
∴146.4÷20=7.32≈7.3(小时).
答:(1)求该海轮从A处到B处的航行过程中与小岛C之间的最短距离是60海里;
(2)如果该海轮以每小时20海里的速度从B处沿BC方向行驶,求它从B处到达小岛C的航行时间约为7.3小时.
7.解:(1)过点B作BE⊥PQ于E,作BF∥AP交PQ于点F.
∵AB∥PQ,BF∥AP,
∴四边形APFB是平行四边形,
∴PF=AB=2千米,∠EFB=∠EPA=20°,
∴FQ=PQ﹣PF=30×﹣2=3(千米).
在△BFQ中,∵∠BFQ=20°,∠FQB=90°+35°=125°,
∴∠FBQ=180°﹣∠BFQ﹣∠FQB=35°,
设BE=x,FQ=FE﹣QE,FE=x tan70°,QE=35×tan35°,
可得x tan70°﹣35×tan35°=3,
解得x=.
答:点P到河岸线l的距离是千米;
(2)∵BQ=千米,游轮的速度为30千米/小时,
∴该游轮按原速度从点Q驶向码头B的时间为:÷30=(小时).
答:若该游轮按原速度从点Q驶向码头B,则它至少需要小时才能到达码头B.
8.解:(1)如图,过点P作PD⊥AB于点D.
在Rt△PBD中,∠BDP=90°,∠PBD=90°﹣45°=45°,
∴BD=PD=3千米.
在Rt△PAD中,∠ADP=90°,∠PAD=90°﹣60°=30°,
∴AD=PD=3千米,PA=6千米.
∴AB=BD+AD=3+3(千米);
(2)如图,过点B作BF⊥AC于点F.
根据题意得:∠ABC=105°,
在Rt△ABF中,∠AFB=90°,∠BAF=30°,
∴BF=AB=千米,AF=AB= 千米.
在△ABC中,∠C=180°﹣∠BAC﹣∠ABC=45°.
在Rt△BCF中,∠BFC=90°,∠C=45°,
∴CF=BF=千米,
∴PC=AF+CF﹣AP=3千米.
故小船沿途考察的时间为:3÷=3(小时).
9.解:(1)作CD⊥BA交BA的延长线于点D,
由题意可得,BC=120米,∠CBD=30°,
则CD=60米,
∵∠DCA=30°,
∴AC=米,
即此时点A到点C的距离是40米;
(2)作A′N⊥BC于点N,作A′E⊥BA交BA的延长线于点E,
由题意可得,
∠1=30°,∠EA′B=′75°,∠EA′A=30°,∠CBD=30°,
则∠AA′B=45°,
∴∠2=15°,
∴∠A′BE=15°,
∴A′N=A′E,
设AA′=x,
则A′E=,
∴A′N=,
∴CA′=,
∵CA=,
∴x+x=40,
得x=60﹣20,
答:此时小明所乘坐的小船走的距离是(60﹣20)米.
10.解:(1)∵B位于P点南偏东24.5°方向,
∴∠BPQ=90°﹣24.5°=65.5°,
又∵B位于Q点南偏西41°方向,
∴∠PQB=90°﹣41°=49°,
∴∠PBQ=180°﹣65.5°﹣49°=65.5°,即∠PBQ=∠BPQ,
∴BQ=PQ=1200(m);
(2)∵点P处测得A在正北方向,
∴∠APQ=90°.在Rt△APQ中,cos∠AQP≈0.75
∴AQ=1200÷0.75=1600,
∵在点Q处,测得A位于北偏西49°方向,B位于南偏西41°方向,
∴∠AQB=90°,在Rt△ABQ中,
AB===2000(m)
答:A,B间的距离约为2000m.
11.解:(1)过点A作AD⊥BC,垂足为D,
在Rt△ABD中,由题意可知∠DBA=30°,
∴AD=AB=×240=120(km),
∵AD=120<150,
∴A城将受这次沙尘暴的影响;
(2)设点E,F是以A为圆心,150km为半径的圆与CB的交点,连接AE,AF,
由题意得DE==90(km),
∴EF=2DE=2×90=180(km),
∴A城受沙尘暴影响的时间为:180÷12=15(时),
答:A城将受到这次沙尘暴的影响,影响的时间为15时.
12.解:(1)过点A作AE⊥DB,交DB的延长线于E,
在Rt△AEB中,∵∠AEB=90°,∠EAB=50°,AB=10,
∴AE=AB cos50°=10×0.643=6.43(nmile),
答:两条航线间的距离为6.43(nmile);
(2)当甲乙两船的位置垂直时,两船之间的距离最短,过C作CF⊥BD于F.
∵BE=AB sin50°=7.66,
AC=24×=8,BD=15×=5,
∴DF=BD+BE﹣AC=4.66,
设还需要t小时才能使两船的距离最短,
则有:24t﹣15t=4.66,
解得t=0.52(h),
答:还需要0.52h才能使两船的距离最短.
13.解:过点A作AF⊥CE,交CE于点F,过点B作BG⊥AF,交AF于点G,则FG=BC=10.
由题意得∠ADE=α,∠E=45°.
设AF=x.
∵∠E=45°,
∴EF=AF=x.
在Rt△ADF中,∵tan∠ADF=,
∴DF==,
∵DE=13.3,
∴x+=13.3.
∴x=11.4.
∴AG=AF﹣GF=11.4﹣10=1.4.
∵∠ABC=120°,
∴∠ABG=∠ABC﹣∠CBG=120°﹣90°=30°.
∴AB=2AG=2.8,
答:灯杆AB的长度为2.8米.
14.解:作EF⊥AC于点F,
根据题意,CE=20×15=300米,
∵i=1:1,
∴tan∠CED=1,
∴∠CED=∠DCE=45°,
∵∠ECF=90°﹣45°﹣15°=30°,
∴EF=CE=150米,
∵∠CEF=60°,∠AEB=30°,
∴∠AEF=180°﹣45°﹣60°﹣30°=45°,
∴AF=EF=150米,
∴AE=(米),
∴AB=×150≈105.8(米).
答:建筑地所在山坡AE的高度AB约为105.8米.
15.解:延长AD交BC的延长线于E,作DF⊥BE于F,
∵∠BCD=150°,
∴∠DCF=30°,又CD=4m,
∴DF=2m,CF==2(m),
由题意得∠E=30°,
∴EF==2,
∴BE=BC+CF+EF=(6+4)m,
∴AB=BE×tanE=(6+4)×=2+4≈7.5(米),
答:电线杆的高度为7.5米.
16.解:(1)过点A作AH⊥PO,垂足为点H,
∵斜坡AP的坡度为1:2.4,
∴,
设AH=5k,则PH=12k,由勾股定理,得AP=13k,
∴13k=26,
解得k=2,
∴AH=10,
答:坡顶A到地面PQ的距离为10米.
(2)延长BC交PO于点D,
∵BC⊥AC,AC∥PO,
∴BD⊥PO,
∴四边形AHDC是矩形,CD=AH=10,AC=DH,
∵∠BPD=45°,
∴PD=BD,
设BC=x,则x+10=24+DH,
∴AC=DH=x﹣14,
在Rt△ABC中,tan76°=,即≈4.01.
解得x≈19.
答:古塔BC的高度约为19米.
17.解:作AD⊥CB交CB所在直线于点D.
由题知,∠ACD=45°,∠ABD=60°.
在Rt△ACD中,∠ACD=45°,
所以CD=AD=120 m.
在Rt△ABD中,∠ABD=60°,tan60°==,
所以BD=AD=,
所以BC=CD﹣BD=120﹣≈120﹣69.2≈51(m).
答:大桥BC的长度约为51m.
18.解:过点M的水平线交直线AB于点H,
由题意,得∠AMH=∠MAH=45°,∠BMH=30°,AB=3.6,
设MH=x,则AH=x,BH=xtan30°=x,
∴AB=AH﹣BH=x﹣x=3.6,
解得x=,
则旗杆高度MN=x+1=(米)
答:旗杆MN的高度度约为米.
19.解:(1)过B作BG⊥AD于G,
则四边形BGDF是矩形,
∴BG=DF=5米,
∵AB=13米,
∴AG==12米,
∴AB的坡度i==1:2.4;
(2)∵在Rt△BCF中,∠CBF=45°,
∴BF=CF,
∵在Rt△CEF中,∠CEF=60°,
∴EF=CF,
∵BE=4(3﹣)米,
∴BF﹣EF=CF﹣CF=4(3﹣),
解得:CF=12.
∴DC=CF+DF=12+5=17米.
20.解:作CE⊥AO于点E,如右图所示,
∵CE⊥AO,∠FAC=45°,OD=15m,
∴∠CAE=45°,CE=15m,
∴AE=15m,
∵AB=10m
∴BE=5m,
∵∠BOD=90°,∠BDO=30°,OD=15m,
∴BO=15×tan30°=15×=5m,
∴EO=BO﹣BE=5﹣5,
∴CD=EO=5﹣5.
21.解:如图作CH⊥MN于H,CK⊥BM于K.则四边形CHMK是矩形,设MN=a.
在Rt△MNB中,BM=a,
在Rt△BCK中,Ck:BK=3:4,设CK=3k,BK=4k,
∵(3k)2+(4k)2=102,
∴k=2(负根已经舍弃),
∴CK=HM=6,BK=8,KM=CH=8+a,
在Rt△CNH中,tan20°=,
∴=0.4,
解得a≈30(米),
答:镇国寺塔MN的高度为30米.
