2021-2022学年人教版八年级数学上册13.2 画轴对称图形同步测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册13.2 画轴对称图形同步测试卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 508.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 00:00:00 | ||
图片预览




文档简介
13.2 画轴对称图形同步测试卷2021-2022学年人教版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共16小题,共48分)
下列图形中,分别以直线l为对称轴作轴对称,其中错误的是( )
A. B.
C. D.
如图所示是一只停泊在平静水面上的小船,它的“倒影”应是( )
A. B.
C. D.
在学习《画轴对称图形》这一节时,老师要求同学们在一个正方形内利用轴对称变换的性质设计图案.下列设计的图案中,是轴对称图形的是( )
A. B.
C. D.
在如图所示的33方格图中有两个半径相等的圆,再在其余的小方格中画一个相同的圆,使整个图形为轴对称图形,则方法有( )
A. 种 B. 种
C. 种 D. 种
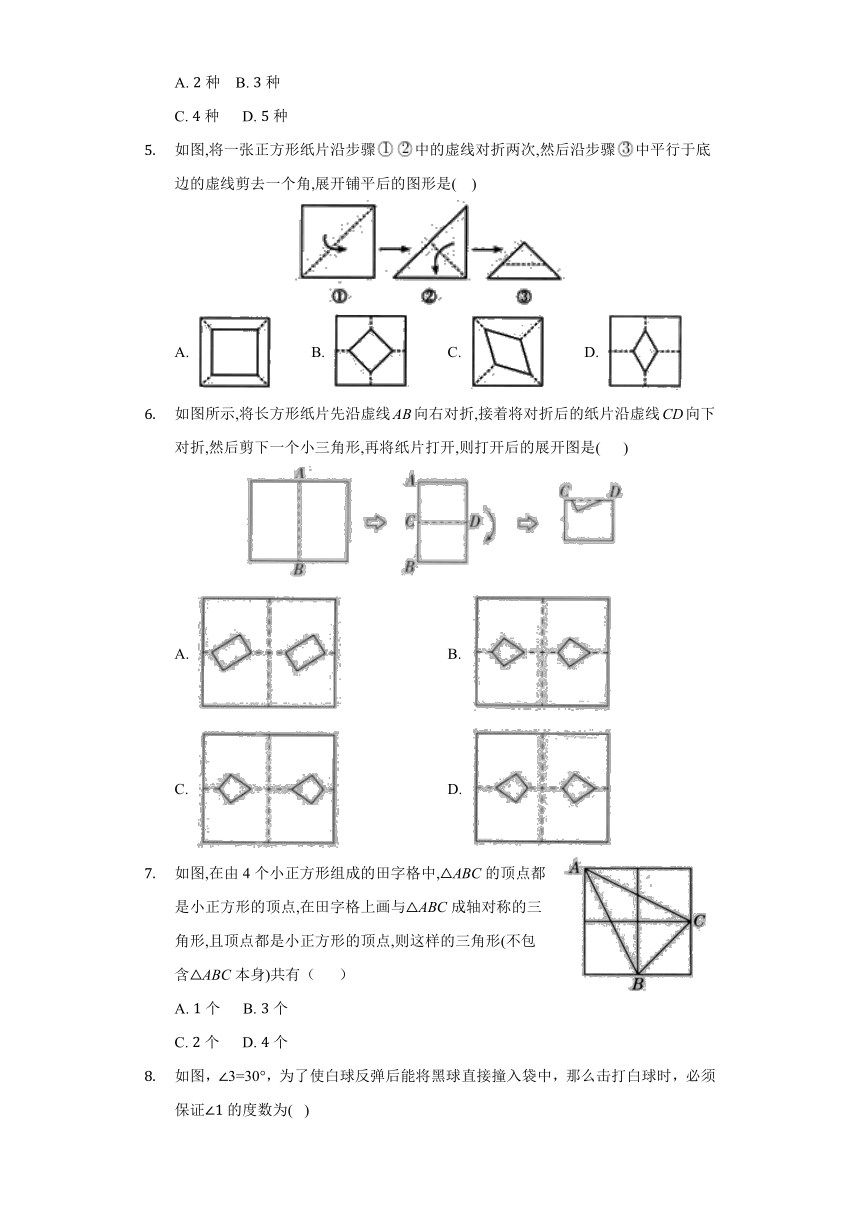
如图,将一张正方形纸片沿步骤中的虚线对折两次,然后沿步骤中平行于底边的虚线剪去一个角,展开铺平后的图形是( )
A. B. C. D.
如图所示,将长方形纸片先沿虚线AB向右对折,接着将对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
A. B.
C. D.
如图,在由4个小正方形组成的田字格中,ABC的顶点都是小正方形的顶点,在田字格上画与ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含ABC本身)共有( )
A. 个 B. 个
C. 个 D. 个
如图,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证的度数为( )
A. B. C. D.
点A和点B(2,-3)关于x轴对称,则A,B两点间的距离是( )
A. B. C. D.
在平面直角坐标系中,将点P(-3,2)向右平移3个单位长度得到点P',则点P'关于x轴对称的点的坐标为( )
A. B. C. D.
点P(-2,1)关于x轴的对称点为,点关于y轴的对称点为,则的坐标是( )
A. B. C. D.
已知P(x,y)在第三象限,且|x|=1,|y|=7,则点P关于x轴对称的点的坐标是( )
A. B. C. D.
ABC的三个顶点的横坐标不变,纵坐标均乘-1后得到DEF,DEF( )
A. 与关于轴对称
B. 与关于轴对称
C. 与关于原点对称
D. 沿轴的负方向平移了个单位长度
如图,△OAB和△OCB关于x轴对称,△OCD和△OED关于y轴对称,若点E的坐标为(4,-6),则点A的坐标为()
A. B.
C. D.
如图,在平面直角坐标系中,ABC的顶点都在格点上.如果将ABC先沿y轴翻折,再向上平移3个单位长度,得到A'B'C',那么点B的对应点B'的坐标为( )
A. B.
C. D.
在平面直角坐标系内,已知在y轴与直线x=3(直线上各点的横坐标都为3)之间有一点M(a,3),如果该点关于直线x=3的对称点N的坐标为(5,3),那么a的值为( )
A. B. C. D.
二、填空题(本大题共3小题,共9分)
已知(a-1,4)和(2,b)关于x轴对称,则的值为 .
已知正方形ABCD在坐标平面上的位置如图所示,x轴、y轴分别是正方形的两条对称轴.若点A的坐标为(2,2),则点B的坐标为 ,点C的坐标为 ,点D的坐标为 .
如图,在平面直角坐标系中,对ABC进行循环往复的轴对称变换.若原来点A的坐标是(a,b),经过第1次变换后所得的点的坐标是(a,-b),则经过第2020次变换后所得的点的坐标是 .
三、解答题(本大题共7小题,共63分)
在下面各图中画出A'B'C',使A'B'C'与ABC关于直线成轴对称图形.
如图,在网格中有两个全等的图形(阴影部分),用这两个图形拼成轴对称图形,试分别在图1、图2中画出不同的拼法.
如图,在正方形网格中,每个小正方形的边长都是1,网格中有一条直线,ABC的三个顶点A,B,C均在格点处.
(1)画出ABC关于直线的对称图形A'B'C'.
(2)求A'B'C'的面积.
图、图、图都是33的正方形网格,每个小正方形的顶点称为格点.A,B,C均为格点,在给定的网格中,按下列要求画图:
(1)在图中,画一条不与AB重合的线段MN,使MN与AB关于某条直线对称,且M,N为格点;
(2)在图中,画一条不与AC重合的线段PQ,使PQ与AC关于某条直线对称,且P,Q为格点;
(3)在图中,画一个DEF,使DEF与ABC关于某条直线对称,且D,E,F为格点.
如图,在边长为1的小正方形网格中,AOB的顶点均在格点上.
(1)B点关于y轴的对称点坐标为 ;
(2)作出将AOB向左平移3个单位长度后关于x轴对称的;
(3)求的面积.
如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如果ABC三个顶点的坐标分别是A(-2,0), B(-1,0),C(-1,2),ABC关于y轴对称的图形是,关于直线l对称的图形是,在坐标系中画出,并写出三个顶点的坐标;
(2)如果点P的坐标是(-a,0),其中,点P关于y轴的对称点是,点关于直线l的对称点是,求的长.
在棋盘中建立如图所示的平面直角坐标系,三颗棋子A,O,B的位置如图所示,它们的坐标分别是(-1,1),(0,0)和(1,0).
(1)如图,添加棋子C,使A,O,B,C四颗棋子成为一个轴对称图形,请在图中画出该图形的对称轴.
(2)在其他格点位置添加一颗棋子P,使A,O,B,P四颗棋子成为一个轴对称图形,请直接写出棋子P的位置的坐标.(写出2个即可)
参考答案
1.【答案】C
2.【答案】B
3.【答案】C
4.【答案】D
5.【答案】A
6.【答案】D
7.【答案】B
8.【答案】C
9.【答案】C
10.【答案】A
11.【答案】B
12.【答案】A
13.【答案】A
14.【答案】B
15.【答案】C
16.【答案】D
17.【答案】-1
18.【答案】(2,-2)
(-2,-2)
(-2,2)
19.【答案】(a,b)
20.【答案】解:A'B'C'如图所示.
21.【答案】解:不同的画法例举如下:(答案不唯一,合理即可)
22.【答案】解:(1)如图,A'B'C'即为所求.
(2)=5.
23.【答案】解:(1)如图,MN即为所求.(答案不唯一)
(2)如图,PQ即为所求.(答案不唯一)
(3)如图,DEF即为所求.(各答案不唯一)
24.【答案】解:(1)(-3,2)
(2)如图,即为所求.
(3)=33-13-23-12=.
25.【答案】解:(1)如图所示,即为所求.三个顶点的坐标分别是(4,0),(5,0),(5,2).
(2)如图,当0< a<3时,
P与关于y轴对称,P(-a,0),
(a,0),
设(b,0),
与关于直线l对称,
=3,即b=6-a,
(6-a,0),
则=6-a-(-a)=6-a+a=6.
26.【答案】解:(1)如图所示:直线l为对称轴;
(2)P(0,-1),P'(-1,-1)都符合题意(答案不唯一).
第11页,共11页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共16小题,共48分)
下列图形中,分别以直线l为对称轴作轴对称,其中错误的是( )
A. B.
C. D.
如图所示是一只停泊在平静水面上的小船,它的“倒影”应是( )
A. B.
C. D.
在学习《画轴对称图形》这一节时,老师要求同学们在一个正方形内利用轴对称变换的性质设计图案.下列设计的图案中,是轴对称图形的是( )
A. B.
C. D.
在如图所示的33方格图中有两个半径相等的圆,再在其余的小方格中画一个相同的圆,使整个图形为轴对称图形,则方法有( )
A. 种 B. 种
C. 种 D. 种
如图,将一张正方形纸片沿步骤中的虚线对折两次,然后沿步骤中平行于底边的虚线剪去一个角,展开铺平后的图形是( )
A. B. C. D.
如图所示,将长方形纸片先沿虚线AB向右对折,接着将对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
A. B.
C. D.
如图,在由4个小正方形组成的田字格中,ABC的顶点都是小正方形的顶点,在田字格上画与ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含ABC本身)共有( )
A. 个 B. 个
C. 个 D. 个
如图,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证的度数为( )
A. B. C. D.
点A和点B(2,-3)关于x轴对称,则A,B两点间的距离是( )
A. B. C. D.
在平面直角坐标系中,将点P(-3,2)向右平移3个单位长度得到点P',则点P'关于x轴对称的点的坐标为( )
A. B. C. D.
点P(-2,1)关于x轴的对称点为,点关于y轴的对称点为,则的坐标是( )
A. B. C. D.
已知P(x,y)在第三象限,且|x|=1,|y|=7,则点P关于x轴对称的点的坐标是( )
A. B. C. D.
ABC的三个顶点的横坐标不变,纵坐标均乘-1后得到DEF,DEF( )
A. 与关于轴对称
B. 与关于轴对称
C. 与关于原点对称
D. 沿轴的负方向平移了个单位长度
如图,△OAB和△OCB关于x轴对称,△OCD和△OED关于y轴对称,若点E的坐标为(4,-6),则点A的坐标为()
A. B.
C. D.
如图,在平面直角坐标系中,ABC的顶点都在格点上.如果将ABC先沿y轴翻折,再向上平移3个单位长度,得到A'B'C',那么点B的对应点B'的坐标为( )
A. B.
C. D.
在平面直角坐标系内,已知在y轴与直线x=3(直线上各点的横坐标都为3)之间有一点M(a,3),如果该点关于直线x=3的对称点N的坐标为(5,3),那么a的值为( )
A. B. C. D.
二、填空题(本大题共3小题,共9分)
已知(a-1,4)和(2,b)关于x轴对称,则的值为 .
已知正方形ABCD在坐标平面上的位置如图所示,x轴、y轴分别是正方形的两条对称轴.若点A的坐标为(2,2),则点B的坐标为 ,点C的坐标为 ,点D的坐标为 .
如图,在平面直角坐标系中,对ABC进行循环往复的轴对称变换.若原来点A的坐标是(a,b),经过第1次变换后所得的点的坐标是(a,-b),则经过第2020次变换后所得的点的坐标是 .
三、解答题(本大题共7小题,共63分)
在下面各图中画出A'B'C',使A'B'C'与ABC关于直线成轴对称图形.
如图,在网格中有两个全等的图形(阴影部分),用这两个图形拼成轴对称图形,试分别在图1、图2中画出不同的拼法.
如图,在正方形网格中,每个小正方形的边长都是1,网格中有一条直线,ABC的三个顶点A,B,C均在格点处.
(1)画出ABC关于直线的对称图形A'B'C'.
(2)求A'B'C'的面积.
图、图、图都是33的正方形网格,每个小正方形的顶点称为格点.A,B,C均为格点,在给定的网格中,按下列要求画图:
(1)在图中,画一条不与AB重合的线段MN,使MN与AB关于某条直线对称,且M,N为格点;
(2)在图中,画一条不与AC重合的线段PQ,使PQ与AC关于某条直线对称,且P,Q为格点;
(3)在图中,画一个DEF,使DEF与ABC关于某条直线对称,且D,E,F为格点.
如图,在边长为1的小正方形网格中,AOB的顶点均在格点上.
(1)B点关于y轴的对称点坐标为 ;
(2)作出将AOB向左平移3个单位长度后关于x轴对称的;
(3)求的面积.
如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如果ABC三个顶点的坐标分别是A(-2,0), B(-1,0),C(-1,2),ABC关于y轴对称的图形是,关于直线l对称的图形是,在坐标系中画出,并写出三个顶点的坐标;
(2)如果点P的坐标是(-a,0),其中,点P关于y轴的对称点是,点关于直线l的对称点是,求的长.
在棋盘中建立如图所示的平面直角坐标系,三颗棋子A,O,B的位置如图所示,它们的坐标分别是(-1,1),(0,0)和(1,0).
(1)如图,添加棋子C,使A,O,B,C四颗棋子成为一个轴对称图形,请在图中画出该图形的对称轴.
(2)在其他格点位置添加一颗棋子P,使A,O,B,P四颗棋子成为一个轴对称图形,请直接写出棋子P的位置的坐标.(写出2个即可)
参考答案
1.【答案】C
2.【答案】B
3.【答案】C
4.【答案】D
5.【答案】A
6.【答案】D
7.【答案】B
8.【答案】C
9.【答案】C
10.【答案】A
11.【答案】B
12.【答案】A
13.【答案】A
14.【答案】B
15.【答案】C
16.【答案】D
17.【答案】-1
18.【答案】(2,-2)
(-2,-2)
(-2,2)
19.【答案】(a,b)
20.【答案】解:A'B'C'如图所示.
21.【答案】解:不同的画法例举如下:(答案不唯一,合理即可)
22.【答案】解:(1)如图,A'B'C'即为所求.
(2)=5.
23.【答案】解:(1)如图,MN即为所求.(答案不唯一)
(2)如图,PQ即为所求.(答案不唯一)
(3)如图,DEF即为所求.(各答案不唯一)
24.【答案】解:(1)(-3,2)
(2)如图,即为所求.
(3)=33-13-23-12=.
25.【答案】解:(1)如图所示,即为所求.三个顶点的坐标分别是(4,0),(5,0),(5,2).
(2)如图,当0< a<3时,
P与关于y轴对称,P(-a,0),
(a,0),
设(b,0),
与关于直线l对称,
=3,即b=6-a,
(6-a,0),
则=6-a-(-a)=6-a+a=6.
26.【答案】解:(1)如图所示:直线l为对称轴;
(2)P(0,-1),P'(-1,-1)都符合题意(答案不唯一).
第11页,共11页
