2021-2022学年人教版八年级数学上册13.3.1 等腰三角形同步测试卷 (Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册13.3.1 等腰三角形同步测试卷 (Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 212.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 08:36:21 | ||
图片预览


文档简介
13.3.1 等腰三角形同步测试卷2021-2022学年人教版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共12小题,共36分)
如图,在ABC中,AB=AC,A=,CDAB,则BCD=( )
A. B. C. D.
如图,AD是等腰ABC的顶角平分线,BD=5,则CD等于( )
A. B. C. D.
若等腰三角形的一个内角为,则另外两个内角的度数分别是( )
A. , B. ,或,
C. , D. ,或,
如图,在RtABC中,ACB=,A=,以点B为圆心,BC长为半径画弧,交AB于点D,连接CD,则ACD的度数是( )
A. B. C. D.
如图,AB=AC,AB的垂直平分线MN交AC于点D.若C=,则DBC的度数是( )
A. B. C. D.
“三等分角”大约是在公元前5世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D、E可在槽中滑动.若BDE=,则CDE的度数是( )
A. B. C. D.
已知等腰三角形两边的长分别为3和7,则这个等腰三角形的周长为( )
A. B. C. 或 D. 或
如图是钢架的一部分,为使钢架更加坚固,在其内部添加了一些钢管DE,EF,FG,添加的这些钢管的长度都与BD的长度相等.如果ABC=,那么添加这样的钢管的根数最多是( )
A. B. C. D.
如图,下列条件不能推出ABC是等腰三角形的是( )
A.
B. ,
C. ,
D. ,
如图,在等腰三角形ABC中,BD为ABC的平分线,A=,AB=AC=a,BC=b,则CD=( )
A. B.
C. D.
已知AOB,作AOB的平分线OM,在射线OM上截取线段OC,分别以O,C为圆心,大于OC的长为半径画弧,两弧相交于点E, F.画直线EF,分别交OA于点D,交OB于点G.那么ODG一定是( )
A. 锐角三角形 B. 钝角三角形 C. 等腰三角形 D. 直角三角形
如图,在ABC中,BD平分ABC,EDBC.已知AB=3,AD=1,则AED的周长为( )
A. B.
C. D.
二、填空题(本大题共6小题,共18分)
如图,在ABC中,AB=AC,ADBC,垂足为D.若BAC=,则BAD= .
如图,在ABC中,AB=AC,点D,E都在边BC上,BAD=CAE.若BD=9,则CE的长为 .
定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的特征值.若在等腰ABC中,A=,则它的特征值k= .
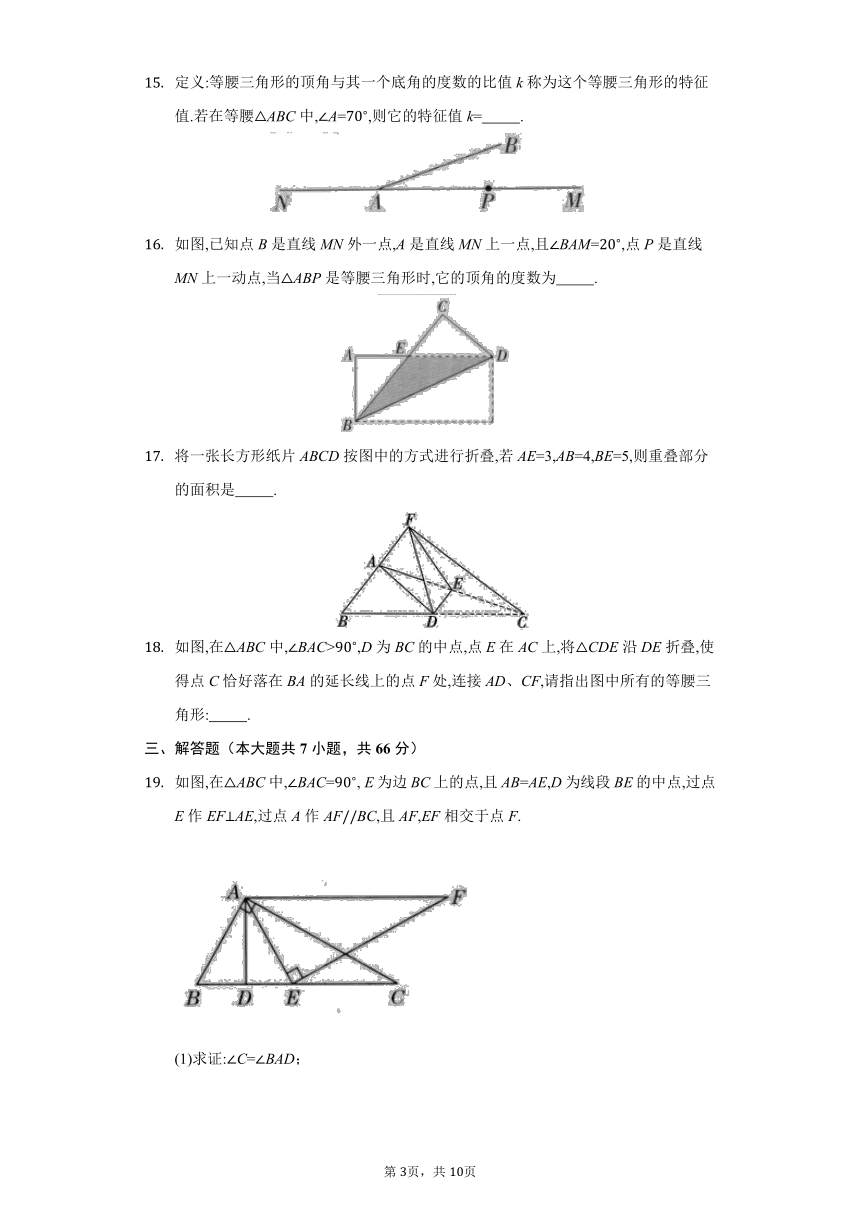
如图,已知点B是直线MN外一点,A是直线MN上一点,且BAM=,点P是直线MN上一动点,当ABP是等腰三角形时,它的顶角的度数为 .
将一张长方形纸片ABCD按图中的方式进行折叠,若AE=3,AB=4,BE=5,则重叠部分的面积是 .
如图,在ABC中,BAC>,D为BC的中点,点E在AC上,将CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连接AD、CF,请指出图中所有的等腰三角形: .
三、解答题(本大题共7小题,共66分)
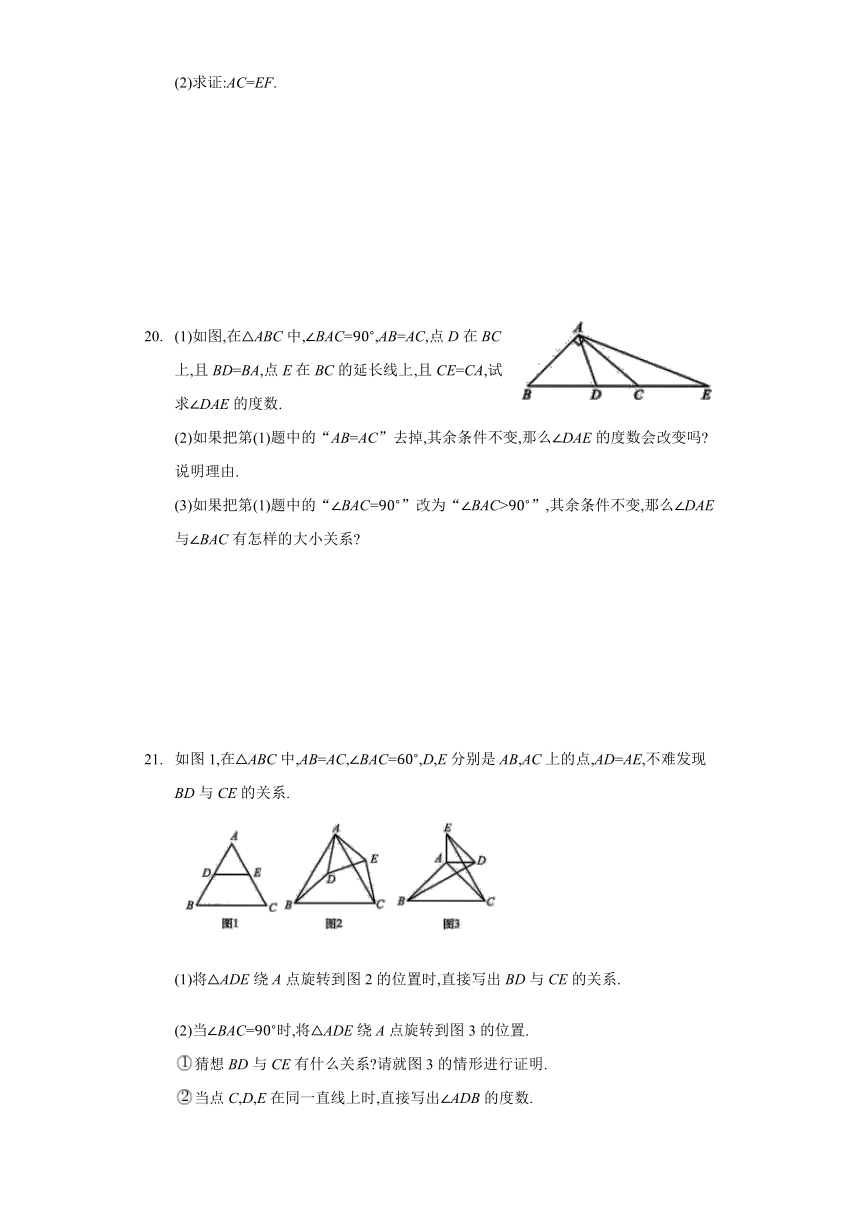
如图,在ABC中,BAC=, E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EFAE,过点A作AFBC,且AF,EF相交于点F.
(1)求证:C=BAD;
(2)求证:AC=EF.
(1)如图,在ABC中,BAC=,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA,试求DAE的度数.
(2)如果把第(1)题中的“AB=AC”去掉,其余条件不变,那么DAE的度数会改变吗 说明理由.
(3)如果把第(1)题中的“BAC=”改为“BAC>”,其余条件不变,那么DAE与BAC有怎样的大小关系
如图1,在ABC中,AB=AC,BAC=,D,E分别是AB,AC上的点,AD=AE,不难发现BD与CE的关系.
(1)将ADE绕A点旋转到图2的位置时,直接写出BD与CE的关系.
(2)当BAC=时,将ADE绕A点旋转到图3的位置.
猜想BD与CE有什么关系 请就图3的情形进行证明.
当点C,D,E在同一直线上时,直接写出ADB的度数.
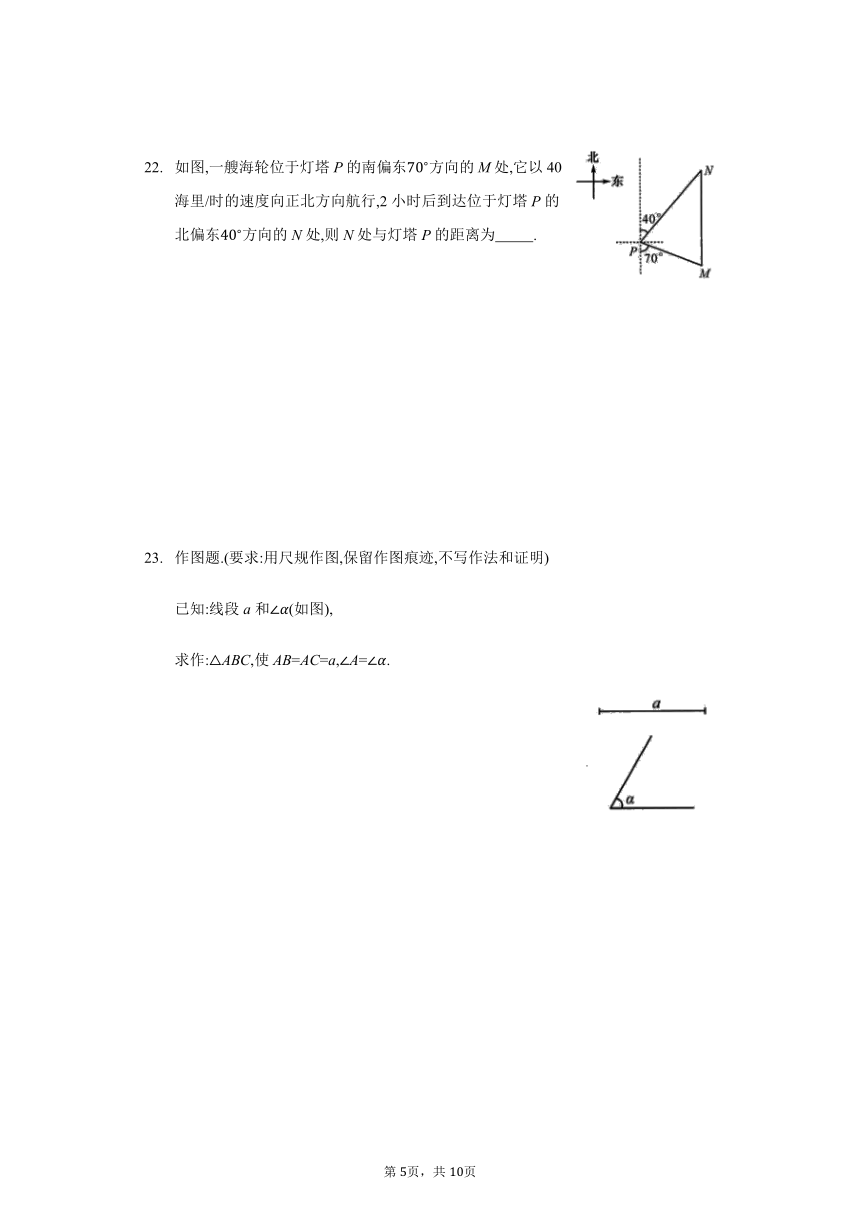
如图,一艘海轮位于灯塔P的南偏东方向的M处,它以40海里/时的速度向正北方向航行,2小时后到达位于灯塔P的北偏东方向的N处,则N处与灯塔P的距离为 .
作图题.(要求:用尺规作图,保留作图痕迹,不写作法和证明)
已知:线段a和(如图),
求作:ABC,使AB=AC=a,A=.
如图,在ABC中,点D,E分别在边AC,AB上,BD与CE相交于点O,给出下列三个条件:EBO=DCO;BE=CD;OB=OC.
(1)上述三个条件中,由哪两个条件可以判定ABC是等腰三角形 (所有成立的情形用序号写出来)
(2)请选择(1)中的一种情形,写出证明过程.
如图,在ABC中,AB=AC=2,B=,点D在线段BC上运动(点D不与B,C两点重合),连接AD,作ADE=,DE交线段AC于点E.
(1)当BDA=时,BAD= ;点D从B向C运动时,BDA逐渐变 (填“大”或“小”).
(2)当ABDDCE时,求CD的长.
(3)在点D的运动过程中,ADE的形状也在改变,当BDA=时,请判断ADE的形状,并证明.
参考答案
1.【答案】D
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】D
6.【答案】D
7.【答案】B
8.【答案】B
9.【答案】C
10.【答案】C
11.【答案】C
12.【答案】C
13.【答案】
14.【答案】9
15.【答案】或
16.【答案】或或
17.【答案】如图,
由折叠可知1=2,
而1=3,
2=3,
ED=EB,
又BE=5,
DE=5,
重叠部分的面积=DEAB=54=10.
故答案为10.
18.【答案】DBF、DFC、EAF、EFC
19.【答案】证明:(1)AB=AE,D为线段BE的中点,
ADBC,
C+DAC=.
BAC=,
BAD+DAC=,
C=BAD;
(2)AFBC,
EAF=AEB.
AB=AE,
B=AEB.
B=EAF.
又AB=AE,BAC=AEF=,
BACAEF(ASA).
AC=EF.
20.【答案】解:(1)DAE=.
(2)不改变.
理由:设∠CAE=x,
∵CA=CE,
∴∠E=∠CAE=x,
∴∠ACB=∠CAE+∠E=2x,
在△ABC中,∠BAC=90°,
∴∠B=90°-∠ACB=90°-2x,
∵BD=BA,
∴∠BAD=∠BDA=(180°-∠B)=x+45°,
在△ABE中,∠BAE=180°-∠B-∠E,
=180°-(90°-2x)-x=90°+x,
∴∠DAE=∠BAE-∠BAD,
=(90°+x)-(x+45°)=45°;
(3)DAE=BAC.
21.【答案】解:(1)BD=CE.
(2)BD=CE,BDCE,
证明:记BD与AC的交点为F,与CE的交点为M,
BAC=DAE=,
BAD=CAE.
在BAD和CAE中,
BAD CAE(SAS).
BD=CE,ABD=ACE.
BAC=,AFB=MFC,
FMC=BAC=.
BDCE.
ADB的度数为或.
22.【答案】80海里
23.【答案】解:如图即为所求:
.
24.【答案】解:(1);.
(2)选,
证明如下:OB=OC,
OBC=OCB.
EBO=DCO,且ABC=EBO+OBC,ACB=DCO+OCB,
ABC=ACB.
AB=AC.
ABC是等腰三角形.
25.【答案】解:(1),小;
(2)ABDDCE,
CD=AB=2.
(3)当BDA=时,ADE是等腰三角形.
证明:∵∠BDA=110°时,
∴∠ADC=70°,
∵∠C=40°,
∴∠DAC=70°,
∴∠ADC=∠DAC=70°,
∴△ADE的形状是等腰三角形.
第9页,共10页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共12小题,共36分)
如图,在ABC中,AB=AC,A=,CDAB,则BCD=( )
A. B. C. D.
如图,AD是等腰ABC的顶角平分线,BD=5,则CD等于( )
A. B. C. D.
若等腰三角形的一个内角为,则另外两个内角的度数分别是( )
A. , B. ,或,
C. , D. ,或,
如图,在RtABC中,ACB=,A=,以点B为圆心,BC长为半径画弧,交AB于点D,连接CD,则ACD的度数是( )
A. B. C. D.
如图,AB=AC,AB的垂直平分线MN交AC于点D.若C=,则DBC的度数是( )
A. B. C. D.
“三等分角”大约是在公元前5世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D、E可在槽中滑动.若BDE=,则CDE的度数是( )
A. B. C. D.
已知等腰三角形两边的长分别为3和7,则这个等腰三角形的周长为( )
A. B. C. 或 D. 或
如图是钢架的一部分,为使钢架更加坚固,在其内部添加了一些钢管DE,EF,FG,添加的这些钢管的长度都与BD的长度相等.如果ABC=,那么添加这样的钢管的根数最多是( )
A. B. C. D.
如图,下列条件不能推出ABC是等腰三角形的是( )
A.
B. ,
C. ,
D. ,
如图,在等腰三角形ABC中,BD为ABC的平分线,A=,AB=AC=a,BC=b,则CD=( )
A. B.
C. D.
已知AOB,作AOB的平分线OM,在射线OM上截取线段OC,分别以O,C为圆心,大于OC的长为半径画弧,两弧相交于点E, F.画直线EF,分别交OA于点D,交OB于点G.那么ODG一定是( )
A. 锐角三角形 B. 钝角三角形 C. 等腰三角形 D. 直角三角形
如图,在ABC中,BD平分ABC,EDBC.已知AB=3,AD=1,则AED的周长为( )
A. B.
C. D.
二、填空题(本大题共6小题,共18分)
如图,在ABC中,AB=AC,ADBC,垂足为D.若BAC=,则BAD= .
如图,在ABC中,AB=AC,点D,E都在边BC上,BAD=CAE.若BD=9,则CE的长为 .
定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的特征值.若在等腰ABC中,A=,则它的特征值k= .
如图,已知点B是直线MN外一点,A是直线MN上一点,且BAM=,点P是直线MN上一动点,当ABP是等腰三角形时,它的顶角的度数为 .
将一张长方形纸片ABCD按图中的方式进行折叠,若AE=3,AB=4,BE=5,则重叠部分的面积是 .
如图,在ABC中,BAC>,D为BC的中点,点E在AC上,将CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连接AD、CF,请指出图中所有的等腰三角形: .
三、解答题(本大题共7小题,共66分)
如图,在ABC中,BAC=, E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EFAE,过点A作AFBC,且AF,EF相交于点F.
(1)求证:C=BAD;
(2)求证:AC=EF.
(1)如图,在ABC中,BAC=,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA,试求DAE的度数.
(2)如果把第(1)题中的“AB=AC”去掉,其余条件不变,那么DAE的度数会改变吗 说明理由.
(3)如果把第(1)题中的“BAC=”改为“BAC>”,其余条件不变,那么DAE与BAC有怎样的大小关系
如图1,在ABC中,AB=AC,BAC=,D,E分别是AB,AC上的点,AD=AE,不难发现BD与CE的关系.
(1)将ADE绕A点旋转到图2的位置时,直接写出BD与CE的关系.
(2)当BAC=时,将ADE绕A点旋转到图3的位置.
猜想BD与CE有什么关系 请就图3的情形进行证明.
当点C,D,E在同一直线上时,直接写出ADB的度数.
如图,一艘海轮位于灯塔P的南偏东方向的M处,它以40海里/时的速度向正北方向航行,2小时后到达位于灯塔P的北偏东方向的N处,则N处与灯塔P的距离为 .
作图题.(要求:用尺规作图,保留作图痕迹,不写作法和证明)
已知:线段a和(如图),
求作:ABC,使AB=AC=a,A=.
如图,在ABC中,点D,E分别在边AC,AB上,BD与CE相交于点O,给出下列三个条件:EBO=DCO;BE=CD;OB=OC.
(1)上述三个条件中,由哪两个条件可以判定ABC是等腰三角形 (所有成立的情形用序号写出来)
(2)请选择(1)中的一种情形,写出证明过程.
如图,在ABC中,AB=AC=2,B=,点D在线段BC上运动(点D不与B,C两点重合),连接AD,作ADE=,DE交线段AC于点E.
(1)当BDA=时,BAD= ;点D从B向C运动时,BDA逐渐变 (填“大”或“小”).
(2)当ABDDCE时,求CD的长.
(3)在点D的运动过程中,ADE的形状也在改变,当BDA=时,请判断ADE的形状,并证明.
参考答案
1.【答案】D
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】D
6.【答案】D
7.【答案】B
8.【答案】B
9.【答案】C
10.【答案】C
11.【答案】C
12.【答案】C
13.【答案】
14.【答案】9
15.【答案】或
16.【答案】或或
17.【答案】如图,
由折叠可知1=2,
而1=3,
2=3,
ED=EB,
又BE=5,
DE=5,
重叠部分的面积=DEAB=54=10.
故答案为10.
18.【答案】DBF、DFC、EAF、EFC
19.【答案】证明:(1)AB=AE,D为线段BE的中点,
ADBC,
C+DAC=.
BAC=,
BAD+DAC=,
C=BAD;
(2)AFBC,
EAF=AEB.
AB=AE,
B=AEB.
B=EAF.
又AB=AE,BAC=AEF=,
BACAEF(ASA).
AC=EF.
20.【答案】解:(1)DAE=.
(2)不改变.
理由:设∠CAE=x,
∵CA=CE,
∴∠E=∠CAE=x,
∴∠ACB=∠CAE+∠E=2x,
在△ABC中,∠BAC=90°,
∴∠B=90°-∠ACB=90°-2x,
∵BD=BA,
∴∠BAD=∠BDA=(180°-∠B)=x+45°,
在△ABE中,∠BAE=180°-∠B-∠E,
=180°-(90°-2x)-x=90°+x,
∴∠DAE=∠BAE-∠BAD,
=(90°+x)-(x+45°)=45°;
(3)DAE=BAC.
21.【答案】解:(1)BD=CE.
(2)BD=CE,BDCE,
证明:记BD与AC的交点为F,与CE的交点为M,
BAC=DAE=,
BAD=CAE.
在BAD和CAE中,
BAD CAE(SAS).
BD=CE,ABD=ACE.
BAC=,AFB=MFC,
FMC=BAC=.
BDCE.
ADB的度数为或.
22.【答案】80海里
23.【答案】解:如图即为所求:
.
24.【答案】解:(1);.
(2)选,
证明如下:OB=OC,
OBC=OCB.
EBO=DCO,且ABC=EBO+OBC,ACB=DCO+OCB,
ABC=ACB.
AB=AC.
ABC是等腰三角形.
25.【答案】解:(1),小;
(2)ABDDCE,
CD=AB=2.
(3)当BDA=时,ADE是等腰三角形.
证明:∵∠BDA=110°时,
∴∠ADC=70°,
∵∠C=40°,
∴∠DAC=70°,
∴∠ADC=∠DAC=70°,
∴△ADE的形状是等腰三角形.
第9页,共10页
