2021-2022学年冀教版九年级数学上册28.3圆心角和圆周角优生辅导测评(Word版 含答案)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学上册28.3圆心角和圆周角优生辅导测评(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 451.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 10:47:45 | ||
图片预览



文档简介
2021-2022学年冀教版九年级数学上册《28.3圆心角和圆周角》优生辅导测评(附答案)
一.选择题(共10小题,满分40分)
1.如图,在三个等圆上各有一条劣弧:弧AB、弧CD、弧EF,如果+=,那么AB+CD与EF的大小关系是( )
A.AB+CD=EF B.AB+CD<EF
C.AB+CD>EF D.大小关系不确定
2.如图,是半圆,O为AB中点,C、D两点在上,且AD∥OC,连接BC、BD.若=62°,则的度数为何?( )
A.56 B.58 C.60 D.62
3.如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为( )
A.cm B.cm C.cm D.4cm
4.如图,AB是半圆的直径,点C是弧AB的中点,点E是弧AC的中点,连接EB,CA交于点F,则=( )
A. B. C.1﹣ D.
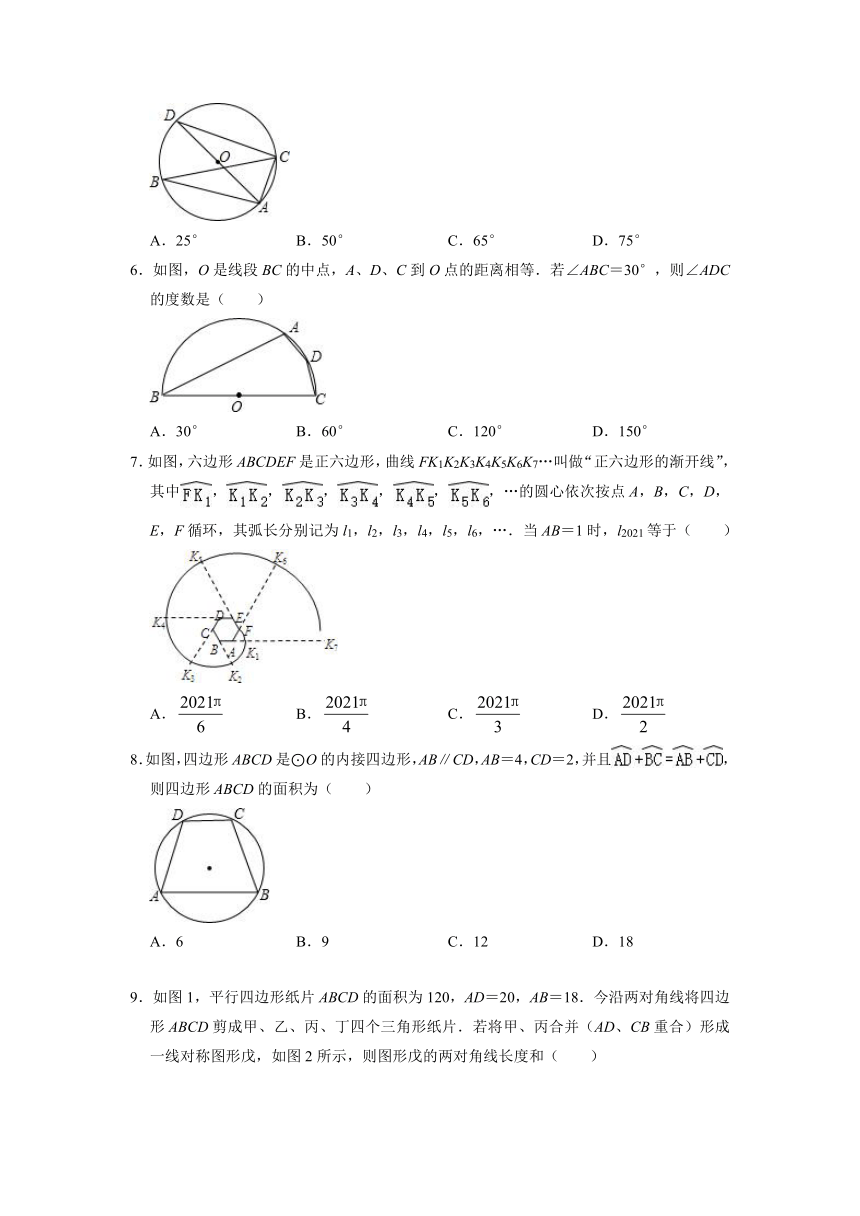
5.如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=25°,则∠CAD的度数为( )
A.25° B.50° C.65° D.75°
6.如图,O是线段BC的中点,A、D、C到O点的距离相等.若∠ABC=30°,则∠ADC的度数是( )
A.30° B.60° C.120° D.150°
7.如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中,,,,,,…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,….当AB=1时,l2021等于( )
A. B. C. D.
8.如图,四边形ABCD是⊙O的内接四边形,AB∥CD,AB=4,CD=2,并且,则四边形ABCD的面积为( )
A.6 B.9 C.12 D.18
9.如图1,平行四边形纸片ABCD的面积为120,AD=20,AB=18.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成一线对称图形戊,如图2所示,则图形戊的两对角线长度和( )
A.26 B.29 C.24 D.25
10.如图,已知⊙O的两条弦AB、CD相交于AB的中点E,且AB=4,DE=CE+3,则CD的长为( )
A.4 B.5 C.8 D.10
二.填空题(共5小题,满分30分)
11.如图,△ABC是⊙O的内接三角形,点D是的中点,已知∠AOB=98°,∠COB=120°,则∠ABD的度数是 度.
12.如图,AB、CD是⊙O的两条互相垂直的弦,圆心角∠AOC=130°,AD,CB的延长线相交于P,∠P= 度.
13.如图,已知A、B两点的坐标分别为(,0)、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为 .
14.如图,在平面直角坐标系中,以点A(0,2)为圆心,2为半径的圆交y轴于点B.已知点C(2,0),点D为⊙A上的一动点,以CD为斜边,在CD左侧作等腰直角三角形CDE,连接BC,则△BCE面积的最小值为 .
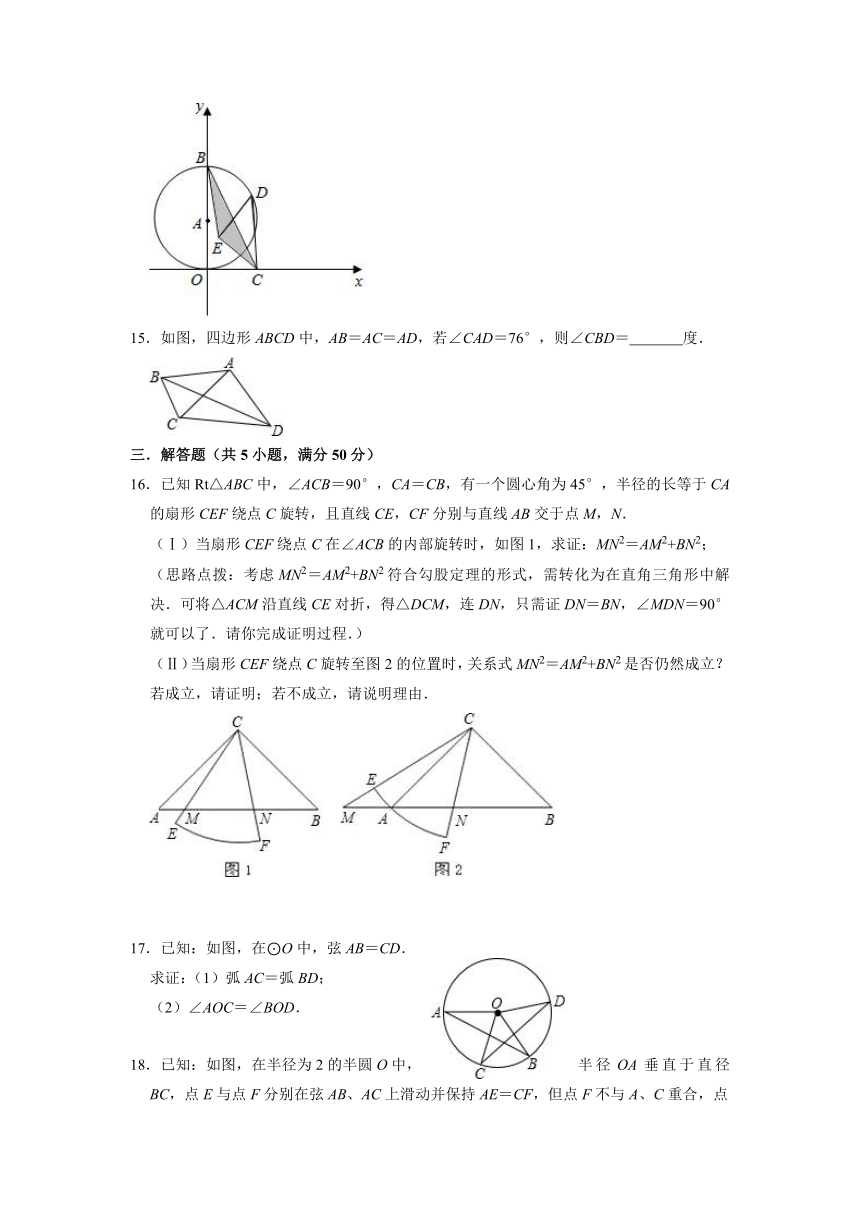
15.如图,四边形ABCD中,AB=AC=AD,若∠CAD=76°,则∠CBD= 度.
三.解答题(共5小题,满分50分)
16.已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(Ⅰ)当扇形CEF绕点C在∠ACB的内部旋转时,如图1,求证:MN2=AM2+BN2;
(思路点拨:考虑MN2=AM2+BN2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.请你完成证明过程.)
(Ⅱ)当扇形CEF绕点C旋转至图2的位置时,关系式MN2=AM2+BN2是否仍然成立?若成立,请证明;若不成立,请说明理由.
17.已知:如图,在⊙O中,弦AB=CD.
求证:(1)弧AC=弧BD;
(2)∠AOC=∠BOD.
18.已知:如图,在半径为2的半圆O中,半径OA垂直于直径BC,点E与点F分别在弦AB、AC上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.
(1)求四边形AEOF的面积.
(2)设AE=x,S△OEF=y,写出y与x之间的函数关系式,求x的取值范围.
19.已知:△ABC是⊙O的内接正三角形,P为弧BC上一点(与点B、C不重合),
(1)如果点P是弧BC的中点,求证:PB+PC=PA;
(2)如果点P在弧BC上移动时,(1)的结论还成立吗?请说明理由.
20.如图,△ABC中,E、F分别是AB、AC上的点.
①AD平分∠BAC,②DE⊥AB,DF⊥AC,③AD⊥EF.
以此三个中的两个为条件,另一个为结论,可构成三个命题,即:
①② ③,①③ ②,②③ ①.
(1)试判断上述三个命题是否正确(直接作答);
(2)请证明你认为正确的命题.
参考答案
一.选择题(共10小题,满分40分)
1.解:如图,在弧EF上取一点M使弧EM=弧CD,
则弧FM=弧AB,
∴AB=FM,CD=EM,
在△MEF中,FM+EM>EF,
∴AB+CD>EF.
故选:C.
2.解:
以AB为直径作圆,如图,作直径CM,连接AC,
∵AD∥OC,
∴∠1=∠2,
∴弧AM=弧DC=62°,
∴弧AD的度数是180°﹣62°﹣62°=56°,
故选:A.
3.解:连接OD,OC,作DE⊥AB于E,OF⊥AC于F,
∵∠CAD=∠BAD(角平分线的性质),
∴=,
∴∠DOB=∠OAC=2∠BAD,
∴△AOF≌△ODE,
∴OE=AF=AC=3(cm),
在Rt△DOE中,DE==4(cm),
在Rt△ADE中,AD==4(cm).
故选:A.
4.解:方法1:连接AE、CE.作AD∥CE,交BE于D.
∵点E是弧AC的中点,
∴可设AE=CE=1,
根据平行线的性质得∠ADE=∠CED=45°.
∴△ADE是等腰直角三角形,
则AD=,BD=AD=.
所以BE=+1.
再根据两角对应相等得△AEF∽△BEA,
则EF==﹣1,BF=2.
所以=.
方法2:过点C作CO⊥AB于点O,
∵AB是半圆的直径,点C是弧AB的中点,
∴点O是圆心.
连接OE,BC,OE与AC交于点M,
∵E为弧AC的中点,
易证OE⊥AC,
∵∠ACB=90°,∠AOE=45°,
∴OE∥BC,
设OM=1,则AM=1,
∴AC=BC=2,OA=,
∴OE=,
∴EM=﹣1,
∵OE∥BC,
∴==.
故选:D.
5.解:∵∠ABC=25°,
∴∠ADC=25°,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠CAD=90°﹣25°=65°.
故选:C.
6.解:∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,即∠ADC=150°.
故选:D.
7.解:根据题意得:L1==,
L2==,
L3===π,
L4==,
按照这种规律可以得到:Ln=,
∴L2021=.
故选:C.
8.解:过O点作DC的垂线交DC于E,交AB于F,交⊙O于M,N,连OD,OA,如图,
∴DE=EC=1,DM弧=MC弧,
∵AB∥CD,
∴OF⊥AB,AD弧=BC弧,
∴AF=BF=2,AN弧=BN弧,
而且,
∴AD弧=DM弧+AN弧,
∴AD弧为半圆MN的一半,
∴∠DOA=90°,
∴Rt△ODE≌Rt△OAF,
∴OE=AF=2,OF=DE=1,即EF=3,
∴梯形ABCD的面积= (2+4) 3=9.
故选:B.
9.解:∵AD=20,平行四边形的面积是120,
∴AD边上的高是6.
∴要求的两对角线长度和是20+6=26.
故选:A.
10.解:设CE=x,则DE=3+x.
根据相交弦定理,得x(x+3)=2×2,
x=1或x=﹣4(不合题意,应舍去).
则CD=3+1+1=5.
故选:B.
二.填空题(共5小题,满分30分)
11.解:∵∠AOB=98°,∠COB=120°,
∴∠AOC=360°﹣∠AOB﹣∠COB=142°;
∴∠ABC=71°;
∵D是的中点,
∴∠CBD=∠BAC;
又∵∠BAC=∠COB=60°,
∴∠CBD=30°;
∴∠ABD=∠ABC+∠CBD=101°.
12.解:设AB与CD交于点E,
∵AB⊥CD,
∴∠AED=∠CEB=90°,
∵圆心角∠AOC=130°,
∴∠ADC=∠ABC=65°,
∴∠BAD=∠DCB=90°﹣65°=25°,
∵∠ADC=∠P+∠DCP,
∴∠P=65°﹣25°=40°.
13.解:∵OB=2,OA=2,
∴AB==4,
∵∠AOP=45°,
∴P点横纵坐标相等,可设为a,即P(a,a),
∵∠AOB=90°,
∴AB是直径,
∴Rt△AOB外接圆的圆心为AB中点,坐标C(,1),
可得P点在圆上,P点到圆心的距离为圆的半径2,
过点C作CF∥OA,过点P作PE⊥OA于E交CF于F,
∴∠CFP=90°,
∴PF=a﹣1,CF=a﹣,PC=2,
∴在Rt△PCF中,利用勾股定理得:(a﹣)2+(a﹣1)2=22,
舍去不合适的根,可得:a=1+,
则P点坐标为(+1,+1).
∵P与P′关于圆心(,1)对称,
∴P′(﹣1,1﹣).
故答案为:(+1,+1)或(﹣1,1﹣)
14.解:如图,设E(m,n),
过点E作EM⊥x轴于M,过点作DN⊥EM,交ME的延长线于N,
∴∠CME=∠END=90°,
∴∠MCE+∠MEC=90°,
∵△CDE是等腰直角三角形,
∴CE=DE,∠CED=90°,
∴∠NED+∠MEC=90°,
∴∠MCE=∠NED,
∴△CME≌△END(AAS),
∴EM=DN=n,CM=EN=2﹣m,
∴D(m+n,n+2﹣m),
∵点D在以A(0,2)为圆心半径为2的圆上,
连接AD,则AD=2,
∴=2,
∴=,
即=,
∴点E在以点O为圆心,为半径的圆上,(到定点(0,0)的距离是的点的轨迹),
∵以点A(0,2)为圆心,2为半径的圆交y轴于点B,
∴B(0,4),
∴OB=4,
∵C(2,0),
∴OC=2,
∴BC=2,
过点O作OH⊥BC于H,
∴OH==,
设点E到BC的距离为h,
∴S△BCE=BC h=×h=h,
∴h最小时,S△BCE最小,而h最小=OH﹣=﹣,
∴S△BCE最小=(﹣)=4﹣,
故答案为:4﹣.
15.解:∵AB=AC=AD,
∴点B,C,D可以看成是以点A为圆心,AB为半径的圆上的三个点,
∴∠CBD是弧CD对的圆周角,∠CAD是弧CD对的圆心角;
∵∠CAD=76°,
∴∠CBD=∠CAD=×76°=38°.
三.解答题(共5小题,满分50分)
16.(Ⅰ)证明:∵将△ACM沿直线CE对折,得△DCM,连DN,
∴△DCM≌△ACM
∴CD=CA,DM=AM,∠DCM=∠ACM,∠CDM=∠A
又∵CA=CB,
∴CD=CB,
∴∠DCN=∠ECF﹣∠DCM=45°﹣∠DCM
∠BCN=∠ACB﹣∠ECF﹣∠ACM
=90°﹣45°﹣∠ACM=45°﹣∠ACM
∴∠DCN=∠BCN
又∵CN=CN,
∴△CDN≌△CBN.
∴DN=BN,∠CDN=∠B.
∴∠MDN=∠CDM+∠CDN=∠A+∠B=90°.
∴在Rt△MDN中,由勾股定理
∴MN2=DM2+DN2,即MN2=AM2+BN2.
(Ⅱ)解:关系式MN2=AM2+BN2仍然成立.
证明:∵将△ACM沿直线CE对折,得△GCM,连GN,
∴△GCM≌△ACM.(8分)
∴CG=CA,GM=AM,∠GCM=∠ACM,∠CGM=∠CAM,
又∵CA=CB,得CG=CB.
∵∠GCN=∠GCM+∠ECF=∠GCM+45°
∴∠BCN=∠ACB﹣∠ACN=90°﹣(∠ECF﹣∠ACM)=45°+∠ACM
得∠GCN=∠BCN.
又∵CN=CN,
∴△CGN≌△CBN.
∴GN=BN,∠CGN=∠B=45°,∠CGM=∠CAM=180°﹣∠CAB=135°,
∴∠MGN=∠CGM﹣∠CGN=135°﹣45°=90°,
∴在Rt△MGN中,由勾股定理,
∴MN2=GM2+GN2,即MN2=AM2+BN2.
17.证明:(1)∵在⊙O中,弦AB=CD,
∴弧AB=弧CD,
∵弧BC=弧CB,
∴弧AC=弧BD;
(2)∵弧AC=弧BD,
∴∠AOC=∠BOD.
18.解:(1)∵BC为半圆O的直径,OA为半径,且OA⊥BC,
∴∠B=∠OAF=45°,OA=OB,
又∵AE=CF,AB=AC,
∴BE=AF,
∴△BOE≌△AOF
∴S四边形AEOF=S△AOB=OB OA=2.
(2)∵BC为半圆O的直径,
∴∠BAC=90°,且AB=AC=2,
y=S△OEF=S四边形AEOF﹣S△AEF=2﹣AE AF=2﹣x(2﹣x)
∴y=x2﹣x+2(0<x<2).
19.解:(1)连OB,OC,如图
∵点P是弧BC的中点,△ABC是⊙O的内接正三角形,
∴AP为⊙O的直径,
∴∠BPO=∠ACB,∠APC=∠ABC,
∵△ABC是⊙O的内接正三角形,
∴∠ACB=∠ABC=60°,
∴∠BPO=∠APC=60°,
∴△OBP和△OPC都是等边三角形,
∴PB=PC=OP=OA,
∴PB+PC=PA;
(2)(1)的结论还成立.理由如下:
截取PE=PC,
∵∠APC=60°,
∴△PEC为等边三角形,
∴CE=CP,∠PCE=60°,
而∠ACB=60°,
∴∠ACE=∠BCP,
而CA=CB,
∴△CAE≌△CBP,
∴AE=PB,
∴PB+PC=PA.
20.解:(1)①② ③,正确;①③ ②,错误;②③ ①,正确.
(2)先证①② ③.如图.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,AD=AD,
∴Rt△ADE≌Rt△ADF.
∴DE=DF,∠ADE=∠ADF.
设AD与EF交于G,则△DEG≌△DFG,
∴∠DGE=∠DGF.
∴∠DGE=∠DGF=90°.
∴AD⊥EF.
再证②③ ①.如图2,
设AD的中点为O,连接OE,OF,
∵DE⊥AB,DF⊥AC,
∴OE,OF分别是Rt△ADE,Rt△ADF斜边上的中线.
∴OE=AD,OF=AD.
即点O到A、E、D、F的距离相等.
∴四点A、E、D、F在以O为圆心,AD为半径的圆上,AD是直径.
∴EF是⊙O的弦.
∵EF⊥AD,
∴∠DAE=∠DAF.
即AD平分∠BAC.
一.选择题(共10小题,满分40分)
1.如图,在三个等圆上各有一条劣弧:弧AB、弧CD、弧EF,如果+=,那么AB+CD与EF的大小关系是( )
A.AB+CD=EF B.AB+CD<EF
C.AB+CD>EF D.大小关系不确定
2.如图,是半圆,O为AB中点,C、D两点在上,且AD∥OC,连接BC、BD.若=62°,则的度数为何?( )
A.56 B.58 C.60 D.62
3.如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为( )
A.cm B.cm C.cm D.4cm
4.如图,AB是半圆的直径,点C是弧AB的中点,点E是弧AC的中点,连接EB,CA交于点F,则=( )
A. B. C.1﹣ D.
5.如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=25°,则∠CAD的度数为( )
A.25° B.50° C.65° D.75°
6.如图,O是线段BC的中点,A、D、C到O点的距离相等.若∠ABC=30°,则∠ADC的度数是( )
A.30° B.60° C.120° D.150°
7.如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中,,,,,,…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,….当AB=1时,l2021等于( )
A. B. C. D.
8.如图,四边形ABCD是⊙O的内接四边形,AB∥CD,AB=4,CD=2,并且,则四边形ABCD的面积为( )
A.6 B.9 C.12 D.18
9.如图1,平行四边形纸片ABCD的面积为120,AD=20,AB=18.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成一线对称图形戊,如图2所示,则图形戊的两对角线长度和( )
A.26 B.29 C.24 D.25
10.如图,已知⊙O的两条弦AB、CD相交于AB的中点E,且AB=4,DE=CE+3,则CD的长为( )
A.4 B.5 C.8 D.10
二.填空题(共5小题,满分30分)
11.如图,△ABC是⊙O的内接三角形,点D是的中点,已知∠AOB=98°,∠COB=120°,则∠ABD的度数是 度.
12.如图,AB、CD是⊙O的两条互相垂直的弦,圆心角∠AOC=130°,AD,CB的延长线相交于P,∠P= 度.
13.如图,已知A、B两点的坐标分别为(,0)、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为 .
14.如图,在平面直角坐标系中,以点A(0,2)为圆心,2为半径的圆交y轴于点B.已知点C(2,0),点D为⊙A上的一动点,以CD为斜边,在CD左侧作等腰直角三角形CDE,连接BC,则△BCE面积的最小值为 .
15.如图,四边形ABCD中,AB=AC=AD,若∠CAD=76°,则∠CBD= 度.
三.解答题(共5小题,满分50分)
16.已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(Ⅰ)当扇形CEF绕点C在∠ACB的内部旋转时,如图1,求证:MN2=AM2+BN2;
(思路点拨:考虑MN2=AM2+BN2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.请你完成证明过程.)
(Ⅱ)当扇形CEF绕点C旋转至图2的位置时,关系式MN2=AM2+BN2是否仍然成立?若成立,请证明;若不成立,请说明理由.
17.已知:如图,在⊙O中,弦AB=CD.
求证:(1)弧AC=弧BD;
(2)∠AOC=∠BOD.
18.已知:如图,在半径为2的半圆O中,半径OA垂直于直径BC,点E与点F分别在弦AB、AC上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.
(1)求四边形AEOF的面积.
(2)设AE=x,S△OEF=y,写出y与x之间的函数关系式,求x的取值范围.
19.已知:△ABC是⊙O的内接正三角形,P为弧BC上一点(与点B、C不重合),
(1)如果点P是弧BC的中点,求证:PB+PC=PA;
(2)如果点P在弧BC上移动时,(1)的结论还成立吗?请说明理由.
20.如图,△ABC中,E、F分别是AB、AC上的点.
①AD平分∠BAC,②DE⊥AB,DF⊥AC,③AD⊥EF.
以此三个中的两个为条件,另一个为结论,可构成三个命题,即:
①② ③,①③ ②,②③ ①.
(1)试判断上述三个命题是否正确(直接作答);
(2)请证明你认为正确的命题.
参考答案
一.选择题(共10小题,满分40分)
1.解:如图,在弧EF上取一点M使弧EM=弧CD,
则弧FM=弧AB,
∴AB=FM,CD=EM,
在△MEF中,FM+EM>EF,
∴AB+CD>EF.
故选:C.
2.解:
以AB为直径作圆,如图,作直径CM,连接AC,
∵AD∥OC,
∴∠1=∠2,
∴弧AM=弧DC=62°,
∴弧AD的度数是180°﹣62°﹣62°=56°,
故选:A.
3.解:连接OD,OC,作DE⊥AB于E,OF⊥AC于F,
∵∠CAD=∠BAD(角平分线的性质),
∴=,
∴∠DOB=∠OAC=2∠BAD,
∴△AOF≌△ODE,
∴OE=AF=AC=3(cm),
在Rt△DOE中,DE==4(cm),
在Rt△ADE中,AD==4(cm).
故选:A.
4.解:方法1:连接AE、CE.作AD∥CE,交BE于D.
∵点E是弧AC的中点,
∴可设AE=CE=1,
根据平行线的性质得∠ADE=∠CED=45°.
∴△ADE是等腰直角三角形,
则AD=,BD=AD=.
所以BE=+1.
再根据两角对应相等得△AEF∽△BEA,
则EF==﹣1,BF=2.
所以=.
方法2:过点C作CO⊥AB于点O,
∵AB是半圆的直径,点C是弧AB的中点,
∴点O是圆心.
连接OE,BC,OE与AC交于点M,
∵E为弧AC的中点,
易证OE⊥AC,
∵∠ACB=90°,∠AOE=45°,
∴OE∥BC,
设OM=1,则AM=1,
∴AC=BC=2,OA=,
∴OE=,
∴EM=﹣1,
∵OE∥BC,
∴==.
故选:D.
5.解:∵∠ABC=25°,
∴∠ADC=25°,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠CAD=90°﹣25°=65°.
故选:C.
6.解:∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,即∠ADC=150°.
故选:D.
7.解:根据题意得:L1==,
L2==,
L3===π,
L4==,
按照这种规律可以得到:Ln=,
∴L2021=.
故选:C.
8.解:过O点作DC的垂线交DC于E,交AB于F,交⊙O于M,N,连OD,OA,如图,
∴DE=EC=1,DM弧=MC弧,
∵AB∥CD,
∴OF⊥AB,AD弧=BC弧,
∴AF=BF=2,AN弧=BN弧,
而且,
∴AD弧=DM弧+AN弧,
∴AD弧为半圆MN的一半,
∴∠DOA=90°,
∴Rt△ODE≌Rt△OAF,
∴OE=AF=2,OF=DE=1,即EF=3,
∴梯形ABCD的面积= (2+4) 3=9.
故选:B.
9.解:∵AD=20,平行四边形的面积是120,
∴AD边上的高是6.
∴要求的两对角线长度和是20+6=26.
故选:A.
10.解:设CE=x,则DE=3+x.
根据相交弦定理,得x(x+3)=2×2,
x=1或x=﹣4(不合题意,应舍去).
则CD=3+1+1=5.
故选:B.
二.填空题(共5小题,满分30分)
11.解:∵∠AOB=98°,∠COB=120°,
∴∠AOC=360°﹣∠AOB﹣∠COB=142°;
∴∠ABC=71°;
∵D是的中点,
∴∠CBD=∠BAC;
又∵∠BAC=∠COB=60°,
∴∠CBD=30°;
∴∠ABD=∠ABC+∠CBD=101°.
12.解:设AB与CD交于点E,
∵AB⊥CD,
∴∠AED=∠CEB=90°,
∵圆心角∠AOC=130°,
∴∠ADC=∠ABC=65°,
∴∠BAD=∠DCB=90°﹣65°=25°,
∵∠ADC=∠P+∠DCP,
∴∠P=65°﹣25°=40°.
13.解:∵OB=2,OA=2,
∴AB==4,
∵∠AOP=45°,
∴P点横纵坐标相等,可设为a,即P(a,a),
∵∠AOB=90°,
∴AB是直径,
∴Rt△AOB外接圆的圆心为AB中点,坐标C(,1),
可得P点在圆上,P点到圆心的距离为圆的半径2,
过点C作CF∥OA,过点P作PE⊥OA于E交CF于F,
∴∠CFP=90°,
∴PF=a﹣1,CF=a﹣,PC=2,
∴在Rt△PCF中,利用勾股定理得:(a﹣)2+(a﹣1)2=22,
舍去不合适的根,可得:a=1+,
则P点坐标为(+1,+1).
∵P与P′关于圆心(,1)对称,
∴P′(﹣1,1﹣).
故答案为:(+1,+1)或(﹣1,1﹣)
14.解:如图,设E(m,n),
过点E作EM⊥x轴于M,过点作DN⊥EM,交ME的延长线于N,
∴∠CME=∠END=90°,
∴∠MCE+∠MEC=90°,
∵△CDE是等腰直角三角形,
∴CE=DE,∠CED=90°,
∴∠NED+∠MEC=90°,
∴∠MCE=∠NED,
∴△CME≌△END(AAS),
∴EM=DN=n,CM=EN=2﹣m,
∴D(m+n,n+2﹣m),
∵点D在以A(0,2)为圆心半径为2的圆上,
连接AD,则AD=2,
∴=2,
∴=,
即=,
∴点E在以点O为圆心,为半径的圆上,(到定点(0,0)的距离是的点的轨迹),
∵以点A(0,2)为圆心,2为半径的圆交y轴于点B,
∴B(0,4),
∴OB=4,
∵C(2,0),
∴OC=2,
∴BC=2,
过点O作OH⊥BC于H,
∴OH==,
设点E到BC的距离为h,
∴S△BCE=BC h=×h=h,
∴h最小时,S△BCE最小,而h最小=OH﹣=﹣,
∴S△BCE最小=(﹣)=4﹣,
故答案为:4﹣.
15.解:∵AB=AC=AD,
∴点B,C,D可以看成是以点A为圆心,AB为半径的圆上的三个点,
∴∠CBD是弧CD对的圆周角,∠CAD是弧CD对的圆心角;
∵∠CAD=76°,
∴∠CBD=∠CAD=×76°=38°.
三.解答题(共5小题,满分50分)
16.(Ⅰ)证明:∵将△ACM沿直线CE对折,得△DCM,连DN,
∴△DCM≌△ACM
∴CD=CA,DM=AM,∠DCM=∠ACM,∠CDM=∠A
又∵CA=CB,
∴CD=CB,
∴∠DCN=∠ECF﹣∠DCM=45°﹣∠DCM
∠BCN=∠ACB﹣∠ECF﹣∠ACM
=90°﹣45°﹣∠ACM=45°﹣∠ACM
∴∠DCN=∠BCN
又∵CN=CN,
∴△CDN≌△CBN.
∴DN=BN,∠CDN=∠B.
∴∠MDN=∠CDM+∠CDN=∠A+∠B=90°.
∴在Rt△MDN中,由勾股定理
∴MN2=DM2+DN2,即MN2=AM2+BN2.
(Ⅱ)解:关系式MN2=AM2+BN2仍然成立.
证明:∵将△ACM沿直线CE对折,得△GCM,连GN,
∴△GCM≌△ACM.(8分)
∴CG=CA,GM=AM,∠GCM=∠ACM,∠CGM=∠CAM,
又∵CA=CB,得CG=CB.
∵∠GCN=∠GCM+∠ECF=∠GCM+45°
∴∠BCN=∠ACB﹣∠ACN=90°﹣(∠ECF﹣∠ACM)=45°+∠ACM
得∠GCN=∠BCN.
又∵CN=CN,
∴△CGN≌△CBN.
∴GN=BN,∠CGN=∠B=45°,∠CGM=∠CAM=180°﹣∠CAB=135°,
∴∠MGN=∠CGM﹣∠CGN=135°﹣45°=90°,
∴在Rt△MGN中,由勾股定理,
∴MN2=GM2+GN2,即MN2=AM2+BN2.
17.证明:(1)∵在⊙O中,弦AB=CD,
∴弧AB=弧CD,
∵弧BC=弧CB,
∴弧AC=弧BD;
(2)∵弧AC=弧BD,
∴∠AOC=∠BOD.
18.解:(1)∵BC为半圆O的直径,OA为半径,且OA⊥BC,
∴∠B=∠OAF=45°,OA=OB,
又∵AE=CF,AB=AC,
∴BE=AF,
∴△BOE≌△AOF
∴S四边形AEOF=S△AOB=OB OA=2.
(2)∵BC为半圆O的直径,
∴∠BAC=90°,且AB=AC=2,
y=S△OEF=S四边形AEOF﹣S△AEF=2﹣AE AF=2﹣x(2﹣x)
∴y=x2﹣x+2(0<x<2).
19.解:(1)连OB,OC,如图
∵点P是弧BC的中点,△ABC是⊙O的内接正三角形,
∴AP为⊙O的直径,
∴∠BPO=∠ACB,∠APC=∠ABC,
∵△ABC是⊙O的内接正三角形,
∴∠ACB=∠ABC=60°,
∴∠BPO=∠APC=60°,
∴△OBP和△OPC都是等边三角形,
∴PB=PC=OP=OA,
∴PB+PC=PA;
(2)(1)的结论还成立.理由如下:
截取PE=PC,
∵∠APC=60°,
∴△PEC为等边三角形,
∴CE=CP,∠PCE=60°,
而∠ACB=60°,
∴∠ACE=∠BCP,
而CA=CB,
∴△CAE≌△CBP,
∴AE=PB,
∴PB+PC=PA.
20.解:(1)①② ③,正确;①③ ②,错误;②③ ①,正确.
(2)先证①② ③.如图.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,AD=AD,
∴Rt△ADE≌Rt△ADF.
∴DE=DF,∠ADE=∠ADF.
设AD与EF交于G,则△DEG≌△DFG,
∴∠DGE=∠DGF.
∴∠DGE=∠DGF=90°.
∴AD⊥EF.
再证②③ ①.如图2,
设AD的中点为O,连接OE,OF,
∵DE⊥AB,DF⊥AC,
∴OE,OF分别是Rt△ADE,Rt△ADF斜边上的中线.
∴OE=AD,OF=AD.
即点O到A、E、D、F的距离相等.
∴四点A、E、D、F在以O为圆心,AD为半径的圆上,AD是直径.
∴EF是⊙O的弦.
∵EF⊥AD,
∴∠DAE=∠DAF.
即AD平分∠BAC.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
