2021-2022学年冀教版九年级数学下册第29章直线与圆的位置关系优生辅导测评 (Word版 含答案)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学下册第29章直线与圆的位置关系优生辅导测评 (Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 416.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 10:59:57 | ||
图片预览



文档简介
2021-2022学年冀教版九年级数学下册《第29章直线与圆的位置关系》
优生辅导测评(附答案)
一.选择题(共10小题,满分40分)
1.如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.+1 B.+ C.2+1 D.2﹣
2.在直角坐标平面内,点A的坐标为(1,0),点B的坐标为(a,0),圆A的半径为2.下列说法中不正确的是( )
A.当a=﹣1时,点B在圆A上 B.当a<1时,点B在圆A内
C.当a<﹣1时,点B在圆A外 D.当﹣1<a<3时,点B在圆A内
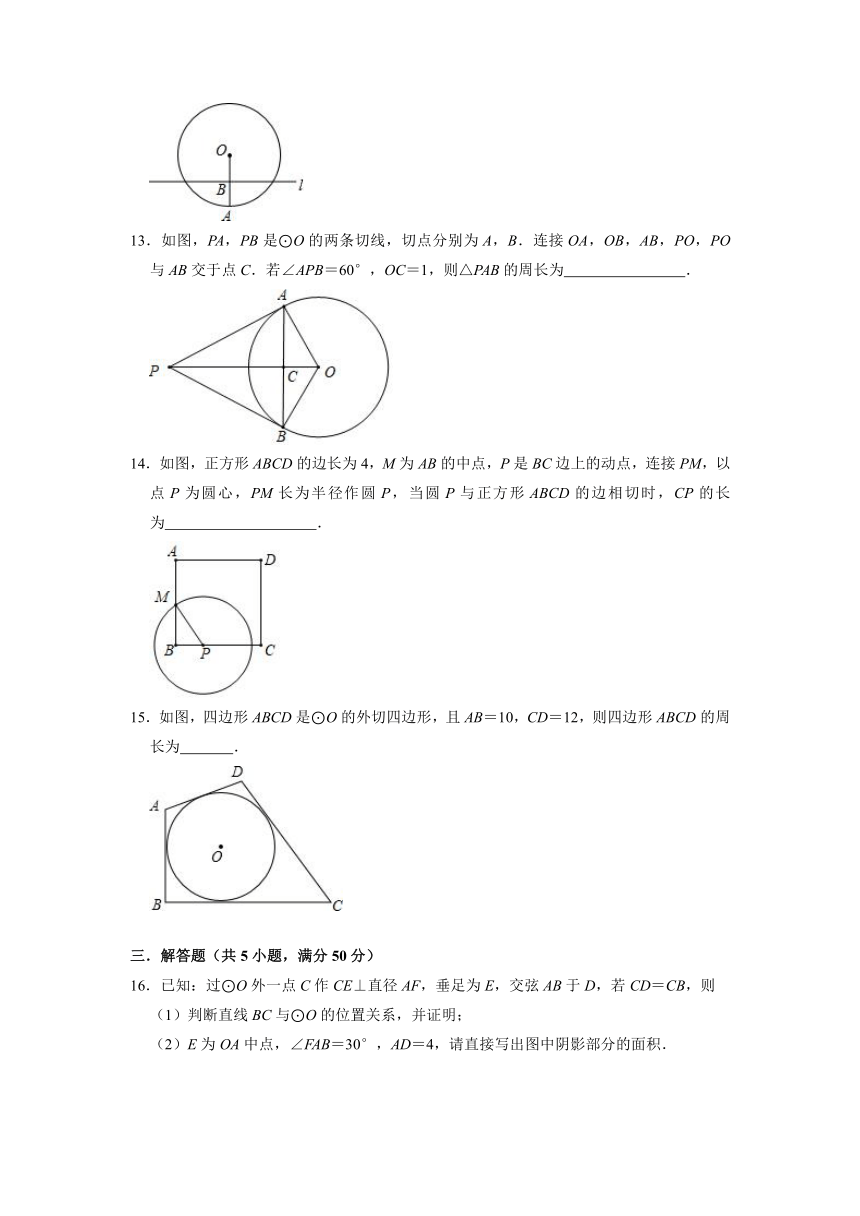
3.圆的半径为5cm,圆心与直线上某一点的距离为5cm,则直线与圆的位置关系是( )
A.相离 B.相切 C.相交或相切 D.相离或相切
4.如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
A.0<CE≤8 B.0<CE≤5 C.3<CE≤8 D.3<CE≤5
5.下列说法中,不正确的个数是( )
①直径是弦;②经过圆内一定点可以作无数条直径;③平分弦的直径垂直于弦;④过三点可以作一个圆;⑤过圆心且垂直于切线的直线必过切点.
A.1个 B.2个 C.3个 D.4个
6.如图,⊙O的半径为4,A、B、C、D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF的值是( )
A.4 B.2 C.4 D.值不确定
7.已知:如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E作弦GF⊥BC交圆与G、F两点,连接CF、BG.则下列结论:①CD⊥AB;②PC是⊙O的切线;③OD∥GF;④弦CF的弦心距等于BG.则其中正确的是( )
A.①②④ B.③④ C.①②③ D.①②③④
8.有下列结论:(1)平分弦的直径垂直于弦;(2)圆周角的度数等于圆心角的一半;(3)等弧所对的圆周角相等;(4)经过三点一定可以作一个圆;(5)三角形的外心到三边的距离相等;(6)垂直于半径的直线是圆的切线.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
9.在Rt△ABC中,AB=6,BC=8,则这个三角形的内切圆的半径是( )
A.5 B.2 C.5或2 D.2或﹣1
10.今有一副三角板如图,中间各有一个直径为2cm的圆洞,现用三角板a的30°角那一头插入三角板b的圆洞中,则三角板a通过三角板b的圆洞那一部分的最大面积为( )cm2(不计三角板厚度)
A. B. C.4 D.
二.填空题(共5小题,满分30分)
11.若⊙A的半径为5,点A的坐标为(3,4),则原点O与⊙A的位置关系是 .
12.如图,⊙O的半径为7cm,直线l⊥OA,垂足为B,OB=4cm,则直线l沿直线OA平移 cm时与⊙O相切.
13.如图,PA,PB是⊙O的两条切线,切点分别为A,B.连接OA,OB,AB,PO,PO与AB交于点C.若∠APB=60°,OC=1,则△PAB的周长为 .
14.如图,正方形ABCD的边长为4,M为AB的中点,P是BC边上的动点,连接PM,以点P为圆心,PM长为半径作圆P,当圆P与正方形ABCD的边相切时,CP的长为 .
15.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为 .
三.解答题(共5小题,满分50分)
16.已知:过⊙O外一点C作CE⊥直径AF,垂足为E,交弦AB于D,若CD=CB,则
(1)判断直线BC与⊙O的位置关系,并证明;
(2)E为OA中点,∠FAB=30°,AD=4,请直接写出图中阴影部分的面积.
17.如图,已知,在以AB为弦的弓形劣弧上取一点M(不包括A,B两点),以M为圆心作圆M和AB相切,分别过A,B作⊙M的切线,两条切线相交于点C.
求证:∠ACB为定值.
18.如图,已知△ABC,以AC为直径的⊙O交AB于点D,点E为的中点,连接CE交AB于点F,且BF=BC.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,sinB=,求CE的长.
19.如图,在Rt△ABC中,∠C=90°,在AC上取一点D,以AD为直径作⊙O,与AB相交于点E,作线段BE的垂直平分线MN交BC于点N,连接EN.
(1)求证:EN是⊙O的切线;
(2)若AC=3,BC=4,⊙O的半径为1.求线段EN与线段AE的长.
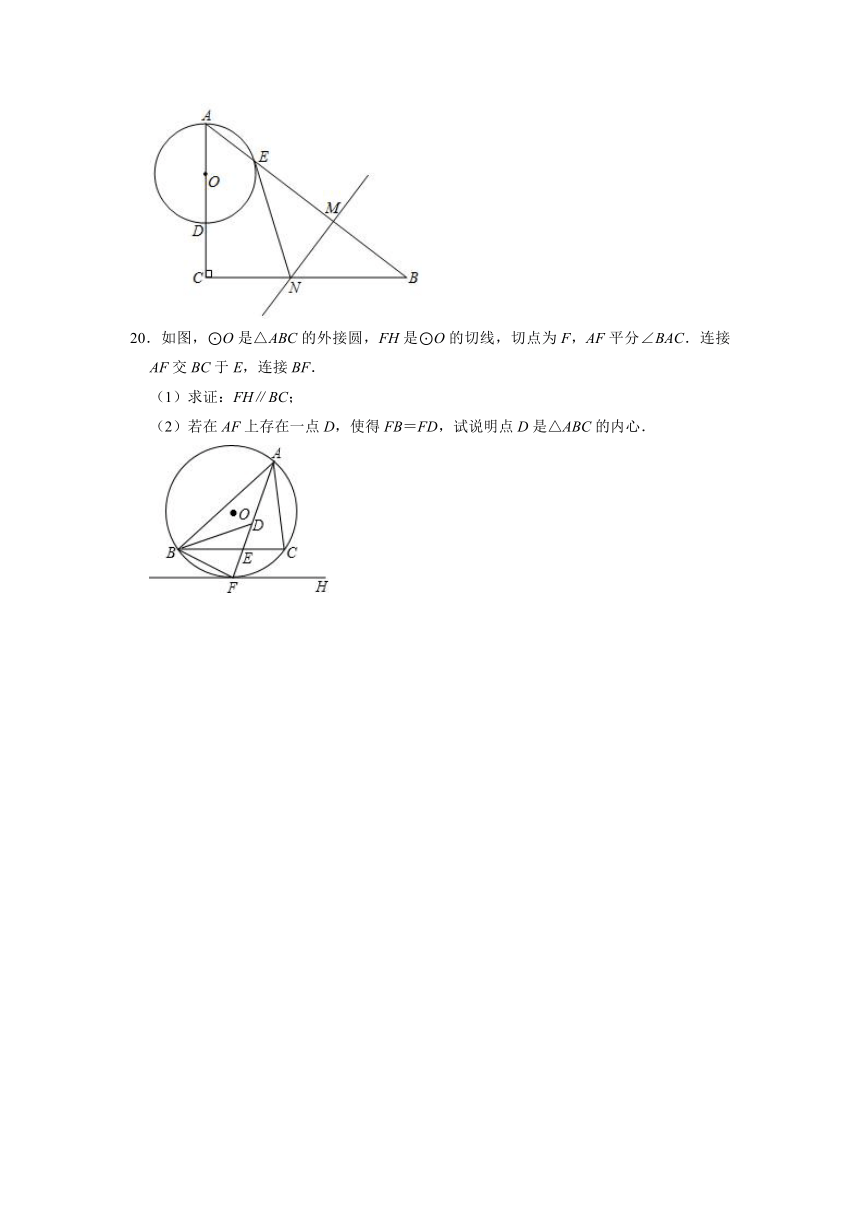
20.如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,AF平分∠BAC.连接AF交BC于E,连接BF.
(1)求证:FH∥BC;
(2)若在AF上存在一点D,使得FB=FD,试说明点D是△ABC的内心.
参考答案
一.选择题(共10小题,满分40分)
1.解:如图,
∵点C为坐标平面内一点,BC=1,
∴C在⊙B上,且半径为1,
取OD=OA=2,连接CD,
∵AM=CM,OD=OA,
∴OM是△ACD的中位线,
∴OM=CD,
当OM最大时,即CD最大,而D,B,C三点共线时,当C在DB的延长线上时,OM最大,
∵OB=OD=2,∠BOD=90°,
∴BD=2,
∴CD=2+1,
∴OM=CD=,即OM的最大值为+;
故选:B.
2.解:如图:
∵A(1,0),⊙A的半径是2,
∴AC=AE=2,
∴OE=1,OC=3,
A、当a=﹣1时,点B在E上,即B在⊙A上,正确,故本选项不合题意;
B、当a=﹣3时,B在⊙A外,即说当a<1时,点B在圆A内错误,故本选项符合题意;
C、当a<﹣1时,AB>2,即说点B在圆A外正确,故本选项不合题意;
D、当﹣1<a<3时,B在⊙A内正确,故本选项不合题意;
故选:B.
3.解:∵圆的半径为5cm,圆心与直线上某一点的距离为5cm,
∴直线与圆有交点
∴当圆心与该点的连线垂直于该直线时,由切线的判定定理可知,直线与圆相切;
当圆心与该点的连线不垂直于该直线时,则由垂线段最短,
可知圆心到该直线的距离小于5,从而直线与圆相交.
故选:C.
4.解:如图,过A作AM⊥BC于N,CN⊥AD于N,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=5,
∴AM=CN,
∵AB=5,cosB=,
∴BM=4,
∵BC=8,
∴CM=BC=4,
∵AM⊥BC,
∴AC=AB=5,
由勾股定理得:AM=CN==3,
∴当以CE为半径的圆C与边AD有两个交点时,半径CE的取值范围是3<CE≤5,
故选:D.
5.解:①直径是特殊的弦.所以①正确,不符合题意;
②只有经过圆心可以作无数条直径.所以②不正确,符合题意;
③平分弦(不是直径)的直径垂直于弦.所以③不正确,符合题意;
④过不在同一条直线上的三点可以作一个圆.所以④不正确,符合题意;
⑤过圆心且垂直于切线的直线必过切点.所以⑤正确,不符合题意.
故选:C.
6.解:当∠ADG=∠BCH=30°时,PE+PF是定值.
理由:连接OA、OB、OC、OD,如图:
∵DG与⊙O相切,
∴∠GDA=∠ABD.
∵∠ADG=30°,
∴∠ABD=30°.
∴∠AOD=2∠ABD=60°.
∵OA=OD,
∴△AOD是等边三角形.
∴AD=OA=4.
同理可得:BC=4.
∵PE∥BC,PF∥AD,
∴△AEP∽△ACB,△BFP∽△BDA.
∴=,=.
∴+=+=1.
∴+=1.
∴PE+PF=4.
∴当∠ADG=∠BCH=30°时,PE+PF=4.
故选:A.
7.解:连接BD、OC、AG,过O作OQ⊥CF于Q,OZ⊥BG于Z,
∵OD=OB,
∴∠ABD=∠ODB,
∵∠AOD=∠OBD+∠ODB=2∠OBD,
∵∠AOD=2∠ABC,
∴∠ABC=∠ABD,
∴弧AC=弧AD,
∵AB是直径,
∴CD⊥AB,
∴①正确;
∵CD⊥AB,
∴∠P+∠PCD=90°,
∵OD=OC,
∴∠OCD=∠ODC=∠P,
∴∠PCD+∠OCD=90°,
∴∠PCO=90°,
∴PC是切线,∴②正确;
假设OD∥GF,则∠AOD=∠FEB=2∠ABC,
∴3∠ABC=90°,
∴∠ABC=30°,
已知没有给出∠B=30°,∴③错误;
∵AB是直径,
∴∠ACB=90°,
∵EF⊥BC,
∴AC∥EF,
∴弧CF=弧AG,
∴AG=CF,
∵OQ⊥CF,OZ⊥BG,
∴CQ=AG,OZ=AG,BZ=BG,
∴OZ=CQ,
∵OC=OB,∠OQC=∠OZB=90°,
∴△OCQ≌△BOZ,
∴OQ=BZ=BG,
∴④正确.
故选:A.
8.解:(1)应强调这条弦不是直径;故本选项错误;
(2)应强调在同圆或等圆中,同弧所对的圆周角的度数等于圆心角的一半;故本选项错误;
(3)等弧弧所对的圆周角的度数等于圆心角的一半;故本选项正确;
(4)必须不在同一条直线上的三个点才能确定一个圆,故本选项错误;
(5)三角形的外心是三角形三条边的垂直平分线的交点,所以三角形的外心到三角形三个顶点的距离相等,故本选项错误;
(6)应该是过圆上一点且垂直圆的半径的直线是圆的切线;故本选项错误;
综上所述,正确的个数是1个;
故选:A.
9.解:设直角三角形ABC内切圆的圆心为点I,半径为r,
三边上的切点分别为D、E、F,
连接ID、IE、IF,
得正方形,则正方形的边长即为r,
如图所示:
当BC为直角边时,
AC==10,
根据切线长定理,得
AD=AF=AB﹣BD=6﹣r,
CE=CF=BC﹣BE=8﹣r,
∴AF+FC=AC=10,
即6﹣r+8﹣r=10,解得r=2;
当BC为斜边时,
AC==2,
根据切线长定理,得
BD=BF=6﹣r,
CE=CF=2﹣r,
∴BC=BF+CF=6﹣r+2﹣r=8,
解得r=﹣1.
答:这个三角形的内切圆的半径是2或﹣1.
故选:D.
10.解:如图,BD为圆洞的直径,BD=2,AB=AD,
过B点作BC⊥AD于C,设BC=x,
在Rt△ABC中,∵∠A=30°,
∴AC=BC=x,AB=2BC=2x,
∴CD=2x﹣x=(2﹣)x,
在△BCD中,[(2﹣)x]2+x2=22,
∴x2=2+,
∴S△ABC=BC AD= x 2x=x2=2+.
故选:A.
二.填空题(共5小题,满分30分)
11.解:∵点A的坐标为A(3,4),
∴OA==5,
∴根据点到圆心的距离等于半径,则知点在圆上.
故答案为:在圆上.
12.解:
延长AO交圆O于C,
当直线l平移到过A点或过C点时,直线l与圆相切,
AB=OA﹣OB=7﹣4=3,BC=OC+0B=7+4=11,
故答案为:3或11.
13.解:∵PA、PB是⊙O的两条切线,
∴OA⊥PA,OB⊥PB,OP平分∠APB,PA=PB,
∵∠APB=60°,
∴△PAB是等边三角形,AB=2AC,PO⊥AB,
∴∠PAB=60°,
∴∠OAC=∠PAO﹣∠PAB=90°﹣60°=30°,
∴AO=2OC,
∵OC=1,
∴AO=2,
∴AC=,
∴AB=2AC=2,
∴△PAB的周长=6.
故答案为:6.
14.解:如图1中,当⊙P与直线CD相切时,设PC=PM=x.
在Rt△PBM中,∵PM2=BM2+PB2,
∴x2=22+(4﹣x)2,
∴x=2.5,
∴CP=2.5;
如图2中当⊙P与直线AD相切时.设切点为K,连接PK,则PK⊥AD,四边形PKDC是矩形.
∴PM=PK=CD=2BM,
∴BM=2,PM=4,
在Rt△PBM中,PB==2,
∴CP=BC﹣PB=4﹣2.
综上所述,CP的长为2.5或4﹣2.
故答案是:2.5或4﹣2.
15.解:∵四边形ABCD是⊙O的外切四边形,
∴AD+BC=AB+CD=22,
∴四边形ABCD的周长=AD+BC+AB+CD=44,
故答案为:44.
三.解答题(共5小题,满分50分)
16.解:(1)直线BC与⊙O相切,
证明:连接OB,
∵CD=CB,
∴∠CBD=∠CDB,
∵CE⊥AF,
∴∠A+∠ADE=90°,
∵∠ADE=∠CDB=∠CBD,
∴∠A+∠CBD=90°,
∵OA=OB,
∴∠OBA=∠A,
∴∠OBA+∠CBD=90°,
∴OB⊥CB,
∵OB是半径,
∴直线BC与⊙O相切;
(2)Rt△AED中,∠A=30°,AD=4,
∴ED==2,
由勾股定理得:AE=2,
∵E为OA中点,
∴OA=OB=4,
设EC交⊙O于M,连接OM,交AB于G,
Rt△OEM中,∵OE=2,OM=4,
∴∠EMO=30°,∠EOM=60°,
∴EM==6,
∵∠A=∠OBA=30°,
∴∠AOB=180°﹣30°﹣30°=120°,
∴∠BOM=60°,
∵∠A=30°,∠AOM=60°,
∴∠AGO=90°,
∴OG=OA=2,AG=6,
∴AB=2AG=12,
∴BD=AB﹣AD=12﹣4=8,
∵∠CDB=∠ADE=60°,CD=CB,
∴△CDB是等边三角形,
∴S阴影=S四边形OECB﹣S△OEM﹣S扇形OMB,
=S四边形OEDB+S△CDB﹣S△OEM﹣S扇形OMB,
=﹣AE ED+﹣OE EM﹣,
=﹣+16﹣﹣8π,
=12﹣2+16﹣6﹣8π,
=.
17.证明:连接AM,BM,
由题意得:M是内心,
∴AM平分∠CAB,BM平分∠ABC,
∴∠CAM=∠BAM,∠CBM=∠ABM,
∴∠AMB=180°﹣∠BAM﹣∠ABM,
∴∠BAM+∠ABM=180°﹣∠AMB,
△ABC中,∠C=180°﹣(∠CAB+∠ACB)=180°﹣2∠BAM﹣2∠ABM=180°﹣2(180°﹣∠AMB)=2∠AMB﹣180°,
∵所在圆是个定圆,弦AB和半径都是定值,
∴∠AMB为定值,
∴∠ACB为定值2∠AMB﹣180°.
18.(1)BC与⊙O相切
证明:连接AE,
∵AC是⊙O的直径
∴∠E=90°,
∴∠EAD+∠AFE=90°,
∵BF=BC,
∴∠BCE=∠BFC,
∵E为弧AD中点,
∴∠EAD=∠ACE,
∴∠BCE+∠ACE=90°,
∴AC⊥BC,
∵AC为直径,
∴BC是⊙O的切线.
(2)解:∵⊙O的半为2
∴AC=4,
∵sinB==,
∴AB=5,
∴BC==3,
∵BF=BC,
∴BF=3,AF=5﹣3=2,
∵∠EAD=∠ACE,∠E=∠E,
∴△AEF∽△CEA,
∴==,
∴EC=2EA,
设EA=x,EC=2x,
由勾股定理得:x2+4x2=16,
x=(负数舍去),
即CE=.
19.解:(1)证明:如图,连接OE,
∵NM是BE的垂直平分线,
BN=EN,
∴∠B=∠NEB,
∵OA=OE
∴∠A=∠OEA,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠OEN=90°,即OE⊥EN,
∵OE是半径,
∴EN是⊙O的切线;
(2)如图,连接ON,
设EN长为x,则BN=EN=x
∵AC=3,BC=4,⊙O的半径为1,
∴CN=4﹣x,OC=AC﹣OA=3﹣1=2,
∴OE2+EN2=OC2+CN2,
∴12+x2=22+(4﹣x)2,
解得x=,
∴EN=.
连接ED,DB,设AE=y,
∵AC=3,BC=4,
∴AB=5,
∵⊙O的半径为1.
∴AD=2,
则DE2=AD2﹣AE2=22﹣y2,
∵CD=AC﹣AD=3﹣2=1,
∴DB2=CD2+BC2=17,
∵AD为直径,
∴∠AED=∠DEB=90°,
∴DE2+EB2=DB2,
即22﹣y2+(5﹣y)2=17,
解得y=,
∴EN=,AE=.
20.解:(1)证明:如图,过点F作直径FN,连接BN.
∵FH是⊙O的切线,
∴FN⊥FH,
∵AF平分∠BAC,
∴∠BAF=∠FAC,
∴=,
由垂径定理得,FN⊥BC,
∴FH∥BC;
(2)连接BD.
∵FB=FD,
∴∠FBD=∠FDB,
又∵∠FBD=∠FBC+∠DBC,∠FDB=∠FAB+∠ABD,∠FAB=∠FBC,
∴∠DBC=∠ABD,
∴BD平分∠ABC,又AF平分∠BAC,
∴点D是△ABC的内心.
优生辅导测评(附答案)
一.选择题(共10小题,满分40分)
1.如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.+1 B.+ C.2+1 D.2﹣
2.在直角坐标平面内,点A的坐标为(1,0),点B的坐标为(a,0),圆A的半径为2.下列说法中不正确的是( )
A.当a=﹣1时,点B在圆A上 B.当a<1时,点B在圆A内
C.当a<﹣1时,点B在圆A外 D.当﹣1<a<3时,点B在圆A内
3.圆的半径为5cm,圆心与直线上某一点的距离为5cm,则直线与圆的位置关系是( )
A.相离 B.相切 C.相交或相切 D.相离或相切
4.如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
A.0<CE≤8 B.0<CE≤5 C.3<CE≤8 D.3<CE≤5
5.下列说法中,不正确的个数是( )
①直径是弦;②经过圆内一定点可以作无数条直径;③平分弦的直径垂直于弦;④过三点可以作一个圆;⑤过圆心且垂直于切线的直线必过切点.
A.1个 B.2个 C.3个 D.4个
6.如图,⊙O的半径为4,A、B、C、D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF的值是( )
A.4 B.2 C.4 D.值不确定
7.已知:如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E作弦GF⊥BC交圆与G、F两点,连接CF、BG.则下列结论:①CD⊥AB;②PC是⊙O的切线;③OD∥GF;④弦CF的弦心距等于BG.则其中正确的是( )
A.①②④ B.③④ C.①②③ D.①②③④
8.有下列结论:(1)平分弦的直径垂直于弦;(2)圆周角的度数等于圆心角的一半;(3)等弧所对的圆周角相等;(4)经过三点一定可以作一个圆;(5)三角形的外心到三边的距离相等;(6)垂直于半径的直线是圆的切线.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
9.在Rt△ABC中,AB=6,BC=8,则这个三角形的内切圆的半径是( )
A.5 B.2 C.5或2 D.2或﹣1
10.今有一副三角板如图,中间各有一个直径为2cm的圆洞,现用三角板a的30°角那一头插入三角板b的圆洞中,则三角板a通过三角板b的圆洞那一部分的最大面积为( )cm2(不计三角板厚度)
A. B. C.4 D.
二.填空题(共5小题,满分30分)
11.若⊙A的半径为5,点A的坐标为(3,4),则原点O与⊙A的位置关系是 .
12.如图,⊙O的半径为7cm,直线l⊥OA,垂足为B,OB=4cm,则直线l沿直线OA平移 cm时与⊙O相切.
13.如图,PA,PB是⊙O的两条切线,切点分别为A,B.连接OA,OB,AB,PO,PO与AB交于点C.若∠APB=60°,OC=1,则△PAB的周长为 .
14.如图,正方形ABCD的边长为4,M为AB的中点,P是BC边上的动点,连接PM,以点P为圆心,PM长为半径作圆P,当圆P与正方形ABCD的边相切时,CP的长为 .
15.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为 .
三.解答题(共5小题,满分50分)
16.已知:过⊙O外一点C作CE⊥直径AF,垂足为E,交弦AB于D,若CD=CB,则
(1)判断直线BC与⊙O的位置关系,并证明;
(2)E为OA中点,∠FAB=30°,AD=4,请直接写出图中阴影部分的面积.
17.如图,已知,在以AB为弦的弓形劣弧上取一点M(不包括A,B两点),以M为圆心作圆M和AB相切,分别过A,B作⊙M的切线,两条切线相交于点C.
求证:∠ACB为定值.
18.如图,已知△ABC,以AC为直径的⊙O交AB于点D,点E为的中点,连接CE交AB于点F,且BF=BC.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,sinB=,求CE的长.
19.如图,在Rt△ABC中,∠C=90°,在AC上取一点D,以AD为直径作⊙O,与AB相交于点E,作线段BE的垂直平分线MN交BC于点N,连接EN.
(1)求证:EN是⊙O的切线;
(2)若AC=3,BC=4,⊙O的半径为1.求线段EN与线段AE的长.
20.如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,AF平分∠BAC.连接AF交BC于E,连接BF.
(1)求证:FH∥BC;
(2)若在AF上存在一点D,使得FB=FD,试说明点D是△ABC的内心.
参考答案
一.选择题(共10小题,满分40分)
1.解:如图,
∵点C为坐标平面内一点,BC=1,
∴C在⊙B上,且半径为1,
取OD=OA=2,连接CD,
∵AM=CM,OD=OA,
∴OM是△ACD的中位线,
∴OM=CD,
当OM最大时,即CD最大,而D,B,C三点共线时,当C在DB的延长线上时,OM最大,
∵OB=OD=2,∠BOD=90°,
∴BD=2,
∴CD=2+1,
∴OM=CD=,即OM的最大值为+;
故选:B.
2.解:如图:
∵A(1,0),⊙A的半径是2,
∴AC=AE=2,
∴OE=1,OC=3,
A、当a=﹣1时,点B在E上,即B在⊙A上,正确,故本选项不合题意;
B、当a=﹣3时,B在⊙A外,即说当a<1时,点B在圆A内错误,故本选项符合题意;
C、当a<﹣1时,AB>2,即说点B在圆A外正确,故本选项不合题意;
D、当﹣1<a<3时,B在⊙A内正确,故本选项不合题意;
故选:B.
3.解:∵圆的半径为5cm,圆心与直线上某一点的距离为5cm,
∴直线与圆有交点
∴当圆心与该点的连线垂直于该直线时,由切线的判定定理可知,直线与圆相切;
当圆心与该点的连线不垂直于该直线时,则由垂线段最短,
可知圆心到该直线的距离小于5,从而直线与圆相交.
故选:C.
4.解:如图,过A作AM⊥BC于N,CN⊥AD于N,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=5,
∴AM=CN,
∵AB=5,cosB=,
∴BM=4,
∵BC=8,
∴CM=BC=4,
∵AM⊥BC,
∴AC=AB=5,
由勾股定理得:AM=CN==3,
∴当以CE为半径的圆C与边AD有两个交点时,半径CE的取值范围是3<CE≤5,
故选:D.
5.解:①直径是特殊的弦.所以①正确,不符合题意;
②只有经过圆心可以作无数条直径.所以②不正确,符合题意;
③平分弦(不是直径)的直径垂直于弦.所以③不正确,符合题意;
④过不在同一条直线上的三点可以作一个圆.所以④不正确,符合题意;
⑤过圆心且垂直于切线的直线必过切点.所以⑤正确,不符合题意.
故选:C.
6.解:当∠ADG=∠BCH=30°时,PE+PF是定值.
理由:连接OA、OB、OC、OD,如图:
∵DG与⊙O相切,
∴∠GDA=∠ABD.
∵∠ADG=30°,
∴∠ABD=30°.
∴∠AOD=2∠ABD=60°.
∵OA=OD,
∴△AOD是等边三角形.
∴AD=OA=4.
同理可得:BC=4.
∵PE∥BC,PF∥AD,
∴△AEP∽△ACB,△BFP∽△BDA.
∴=,=.
∴+=+=1.
∴+=1.
∴PE+PF=4.
∴当∠ADG=∠BCH=30°时,PE+PF=4.
故选:A.
7.解:连接BD、OC、AG,过O作OQ⊥CF于Q,OZ⊥BG于Z,
∵OD=OB,
∴∠ABD=∠ODB,
∵∠AOD=∠OBD+∠ODB=2∠OBD,
∵∠AOD=2∠ABC,
∴∠ABC=∠ABD,
∴弧AC=弧AD,
∵AB是直径,
∴CD⊥AB,
∴①正确;
∵CD⊥AB,
∴∠P+∠PCD=90°,
∵OD=OC,
∴∠OCD=∠ODC=∠P,
∴∠PCD+∠OCD=90°,
∴∠PCO=90°,
∴PC是切线,∴②正确;
假设OD∥GF,则∠AOD=∠FEB=2∠ABC,
∴3∠ABC=90°,
∴∠ABC=30°,
已知没有给出∠B=30°,∴③错误;
∵AB是直径,
∴∠ACB=90°,
∵EF⊥BC,
∴AC∥EF,
∴弧CF=弧AG,
∴AG=CF,
∵OQ⊥CF,OZ⊥BG,
∴CQ=AG,OZ=AG,BZ=BG,
∴OZ=CQ,
∵OC=OB,∠OQC=∠OZB=90°,
∴△OCQ≌△BOZ,
∴OQ=BZ=BG,
∴④正确.
故选:A.
8.解:(1)应强调这条弦不是直径;故本选项错误;
(2)应强调在同圆或等圆中,同弧所对的圆周角的度数等于圆心角的一半;故本选项错误;
(3)等弧弧所对的圆周角的度数等于圆心角的一半;故本选项正确;
(4)必须不在同一条直线上的三个点才能确定一个圆,故本选项错误;
(5)三角形的外心是三角形三条边的垂直平分线的交点,所以三角形的外心到三角形三个顶点的距离相等,故本选项错误;
(6)应该是过圆上一点且垂直圆的半径的直线是圆的切线;故本选项错误;
综上所述,正确的个数是1个;
故选:A.
9.解:设直角三角形ABC内切圆的圆心为点I,半径为r,
三边上的切点分别为D、E、F,
连接ID、IE、IF,
得正方形,则正方形的边长即为r,
如图所示:
当BC为直角边时,
AC==10,
根据切线长定理,得
AD=AF=AB﹣BD=6﹣r,
CE=CF=BC﹣BE=8﹣r,
∴AF+FC=AC=10,
即6﹣r+8﹣r=10,解得r=2;
当BC为斜边时,
AC==2,
根据切线长定理,得
BD=BF=6﹣r,
CE=CF=2﹣r,
∴BC=BF+CF=6﹣r+2﹣r=8,
解得r=﹣1.
答:这个三角形的内切圆的半径是2或﹣1.
故选:D.
10.解:如图,BD为圆洞的直径,BD=2,AB=AD,
过B点作BC⊥AD于C,设BC=x,
在Rt△ABC中,∵∠A=30°,
∴AC=BC=x,AB=2BC=2x,
∴CD=2x﹣x=(2﹣)x,
在△BCD中,[(2﹣)x]2+x2=22,
∴x2=2+,
∴S△ABC=BC AD= x 2x=x2=2+.
故选:A.
二.填空题(共5小题,满分30分)
11.解:∵点A的坐标为A(3,4),
∴OA==5,
∴根据点到圆心的距离等于半径,则知点在圆上.
故答案为:在圆上.
12.解:
延长AO交圆O于C,
当直线l平移到过A点或过C点时,直线l与圆相切,
AB=OA﹣OB=7﹣4=3,BC=OC+0B=7+4=11,
故答案为:3或11.
13.解:∵PA、PB是⊙O的两条切线,
∴OA⊥PA,OB⊥PB,OP平分∠APB,PA=PB,
∵∠APB=60°,
∴△PAB是等边三角形,AB=2AC,PO⊥AB,
∴∠PAB=60°,
∴∠OAC=∠PAO﹣∠PAB=90°﹣60°=30°,
∴AO=2OC,
∵OC=1,
∴AO=2,
∴AC=,
∴AB=2AC=2,
∴△PAB的周长=6.
故答案为:6.
14.解:如图1中,当⊙P与直线CD相切时,设PC=PM=x.
在Rt△PBM中,∵PM2=BM2+PB2,
∴x2=22+(4﹣x)2,
∴x=2.5,
∴CP=2.5;
如图2中当⊙P与直线AD相切时.设切点为K,连接PK,则PK⊥AD,四边形PKDC是矩形.
∴PM=PK=CD=2BM,
∴BM=2,PM=4,
在Rt△PBM中,PB==2,
∴CP=BC﹣PB=4﹣2.
综上所述,CP的长为2.5或4﹣2.
故答案是:2.5或4﹣2.
15.解:∵四边形ABCD是⊙O的外切四边形,
∴AD+BC=AB+CD=22,
∴四边形ABCD的周长=AD+BC+AB+CD=44,
故答案为:44.
三.解答题(共5小题,满分50分)
16.解:(1)直线BC与⊙O相切,
证明:连接OB,
∵CD=CB,
∴∠CBD=∠CDB,
∵CE⊥AF,
∴∠A+∠ADE=90°,
∵∠ADE=∠CDB=∠CBD,
∴∠A+∠CBD=90°,
∵OA=OB,
∴∠OBA=∠A,
∴∠OBA+∠CBD=90°,
∴OB⊥CB,
∵OB是半径,
∴直线BC与⊙O相切;
(2)Rt△AED中,∠A=30°,AD=4,
∴ED==2,
由勾股定理得:AE=2,
∵E为OA中点,
∴OA=OB=4,
设EC交⊙O于M,连接OM,交AB于G,
Rt△OEM中,∵OE=2,OM=4,
∴∠EMO=30°,∠EOM=60°,
∴EM==6,
∵∠A=∠OBA=30°,
∴∠AOB=180°﹣30°﹣30°=120°,
∴∠BOM=60°,
∵∠A=30°,∠AOM=60°,
∴∠AGO=90°,
∴OG=OA=2,AG=6,
∴AB=2AG=12,
∴BD=AB﹣AD=12﹣4=8,
∵∠CDB=∠ADE=60°,CD=CB,
∴△CDB是等边三角形,
∴S阴影=S四边形OECB﹣S△OEM﹣S扇形OMB,
=S四边形OEDB+S△CDB﹣S△OEM﹣S扇形OMB,
=﹣AE ED+﹣OE EM﹣,
=﹣+16﹣﹣8π,
=12﹣2+16﹣6﹣8π,
=.
17.证明:连接AM,BM,
由题意得:M是内心,
∴AM平分∠CAB,BM平分∠ABC,
∴∠CAM=∠BAM,∠CBM=∠ABM,
∴∠AMB=180°﹣∠BAM﹣∠ABM,
∴∠BAM+∠ABM=180°﹣∠AMB,
△ABC中,∠C=180°﹣(∠CAB+∠ACB)=180°﹣2∠BAM﹣2∠ABM=180°﹣2(180°﹣∠AMB)=2∠AMB﹣180°,
∵所在圆是个定圆,弦AB和半径都是定值,
∴∠AMB为定值,
∴∠ACB为定值2∠AMB﹣180°.
18.(1)BC与⊙O相切
证明:连接AE,
∵AC是⊙O的直径
∴∠E=90°,
∴∠EAD+∠AFE=90°,
∵BF=BC,
∴∠BCE=∠BFC,
∵E为弧AD中点,
∴∠EAD=∠ACE,
∴∠BCE+∠ACE=90°,
∴AC⊥BC,
∵AC为直径,
∴BC是⊙O的切线.
(2)解:∵⊙O的半为2
∴AC=4,
∵sinB==,
∴AB=5,
∴BC==3,
∵BF=BC,
∴BF=3,AF=5﹣3=2,
∵∠EAD=∠ACE,∠E=∠E,
∴△AEF∽△CEA,
∴==,
∴EC=2EA,
设EA=x,EC=2x,
由勾股定理得:x2+4x2=16,
x=(负数舍去),
即CE=.
19.解:(1)证明:如图,连接OE,
∵NM是BE的垂直平分线,
BN=EN,
∴∠B=∠NEB,
∵OA=OE
∴∠A=∠OEA,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠OEN=90°,即OE⊥EN,
∵OE是半径,
∴EN是⊙O的切线;
(2)如图,连接ON,
设EN长为x,则BN=EN=x
∵AC=3,BC=4,⊙O的半径为1,
∴CN=4﹣x,OC=AC﹣OA=3﹣1=2,
∴OE2+EN2=OC2+CN2,
∴12+x2=22+(4﹣x)2,
解得x=,
∴EN=.
连接ED,DB,设AE=y,
∵AC=3,BC=4,
∴AB=5,
∵⊙O的半径为1.
∴AD=2,
则DE2=AD2﹣AE2=22﹣y2,
∵CD=AC﹣AD=3﹣2=1,
∴DB2=CD2+BC2=17,
∵AD为直径,
∴∠AED=∠DEB=90°,
∴DE2+EB2=DB2,
即22﹣y2+(5﹣y)2=17,
解得y=,
∴EN=,AE=.
20.解:(1)证明:如图,过点F作直径FN,连接BN.
∵FH是⊙O的切线,
∴FN⊥FH,
∵AF平分∠BAC,
∴∠BAF=∠FAC,
∴=,
由垂径定理得,FN⊥BC,
∴FH∥BC;
(2)连接BD.
∵FB=FD,
∴∠FBD=∠FDB,
又∵∠FBD=∠FBC+∠DBC,∠FDB=∠FAB+∠ABD,∠FAB=∠FBC,
∴∠DBC=∠ABD,
∴BD平分∠ABC,又AF平分∠BAC,
∴点D是△ABC的内心.
