2021-2022学年北师大版八年级数学上册 5.3应用二元一次方程组——鸡兔同笼 同步达标训练(Word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册 5.3应用二元一次方程组——鸡兔同笼 同步达标训练(Word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 169.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 13:21:29 | ||
图片预览




文档简介
2021-2022学年北师大版八年级数学上册《5.3应用二元一次方程组——鸡兔同笼》
同步达标训练(附答案)
1.《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕,共重16两,雀重燕轻.互换其中一只,恰好一样重.问每只雀、燕的重量各为多少?”解:设雀每只x两,燕每只y两,则可列出方程组为( )
A. B. C. D.
2.《孙子算经》中有一道题,原文是“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺.问木长多少尺?设木长x尺,绳长y尺,可列方程组为( )
A. B. C. D.
3.某校举行篮球赛,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.八年级一班在16场比赛中得26分.设该班胜x场,负y场,则根据题意,下列方程组中正确的是( )
A. B. C. D.
4.我国古代数学著作《九章算术》“盈不足”一章中记载:“今有大器五小器一容三斛,大器一小器五容二斛,问大小器各容几何”.意思是:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛,1个大桶加上5个小桶可以盛酒2斛.问1个大桶、1个小桶分别可以盛酒多少斛?设1个大桶盛酒x斛,1个小桶盛酒y斛,下列方程组正确的是( )
A. B. C. D.
5.《九章算术》“盈不足”一卷中有这样一个问题:“今有善田一亩,价三百;恶田七亩,价五百.今并买一顷,价钱一万.问善、恶田各几何?”意思是:“今有好田1亩,价值300钱;坏田7亩,价值500钱.今共买好、坏田1顷(1顷=100亩),总价值10000钱.问好、坏田各买了多少亩?设好田买了x亩,坏田买了y亩,则下面所列方程组正确的是( )
A.B. C. D.
6.《九章算术》是古代中国第一部自成体系的数学专著,其中《卷第八方程》记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,问甲、乙持钱各几何?”译文是:今有甲、乙两人持钱不知道各有多少,甲若得到乙所有钱的,则甲有50钱,乙若得到甲所有钱的,则乙也有50钱.问甲、乙各持钱多少?设甲持钱数为x钱,乙持钱数为y钱,列出关于x、y的二元一次方程组是( )
A. B.
C. D.
7.《九章算术》中记载了一个问题,大意是甲、乙两人各带了若干钱.若甲得到乙所有钱的一半,则甲共有钱50.若乙得到甲所有钱的,则乙也共有钱50.甲、乙两人各带了多少钱?设甲带了钱x,乙带了钱y,依题意,下面所列方程组正确的是( )
A. B.
C. D.
8.《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步.问:人与车各几何?译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行,问:人与车各多少?设有x辆车,人数为y,根据题意可列方程组为( )
A. B.
C. D.
9.某公司上半年生产甲、乙两种型号的无人机若干架,已知甲种型号无人机架数比总架数的一半多11架,乙种型号无人机架数比总架数的三分之一少2架.设甲种型号无人机x架,乙种型号无人机y架,根据题意可列出的方程组是( )
A. B.
C. D.
10.《九章算术》卷八方程第十题原文为:“今有甲、乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而亦钱五十.问:甲、乙持钱各几何?”题目大意是:甲、乙两人各带了若干钱.如果甲得到乙所有钱的一半,那么甲共有钱50;如果乙得到甲所有钱的,那么乙也共有钱50.问:甲、乙两人各带了多少钱?设甲、乙两人持钱的数量分别为x,y,则可列方程组为( )
A.B.C.D.
11.中国古代人民在生产生活中发现了许多数学问题,在《孙子算经》中记载了这样一个问题,大意为:有若干人乘车,若每车乘坐3人,则2辆车无人乘坐;若每车乘坐2人,则9人无车可乘,问共有多少辆车,多少人,设共有x辆车,y人,则可列方程组为( )
A.B. C.D.
12.我国古代数学名著《九章算术》上有这样一个问题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”其大意是:今有醇酒(优质酒)1斗,价值50钱;行酒(劣质酒)1斗,价值10钱.现用30钱,买得2斗酒.问醇酒、行酒各能买得多少?设醇酒为x斗,行酒为y斗,根据题意,可列方程组为 .
13.《九章算术》是我国东汉初年编订的一部数学经典著作,其中一次方程组是用算筹布置而成,如图(1)所示的算筹图用我们现在所熟悉的方程组表示出来,就是,类似的,图(2)所示的算筹图用方程组表示出来,就是 .
14.《九章算术》记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?”其大意是:“今有甲乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的钱数为50;而甲把其的钱给乙,则乙的钱数也为50.问甲、乙各有多少钱?”设甲的钱数为x,乙的钱数为y,根据题意,可列方程组为 .
15.《孙子算经》记载:今有3人共车,二车空;二人共车,九人步,问人与车各几何?译文:今有若干人乘车,若每三人共乘一辆车,最终剩余2辆车;若每2人共乘一辆车,最终剩余9人无车可乘.问共有多少人?多少辆车?若设有x人,y辆车,则可列方程组为 .
16.《九章算术》是我国古代一部著名的算书,它的出现标志着中国古代数学形成了完整的体系.其中卷八方程[七]中记载:“今有牛五、羊二,直金十两.牛二、羊五,直金八两.牛、羊各直金几何?”题目大意是:5头牛、2只羊共值金10两.2头牛、5只羊共值金8两.每头牛、每只羊各值金多少两?设1头牛值金x两,1只羊值金y两,则可列方程组为 .
17.山西省小麦种植面积在1000万亩以上,端午前后是小麦收割的季节.2台大收割机和4台小收割机同时工作2h共收割小麦48亩,3台大收割机和5台小收割机同时工作1h共收割小麦33亩.1台大收割机和1台小收割机每小时各收割小麦多少亩?设1台大收割机每小时收割小麦x亩,1台小收割机每小时收割小麦y亩,则根据题意可列方程组 .
18.《孙于算经》是中国古代重要的数学著作,其中一道题的原文是:“今三人共车,两车空;二人共车,九人步,问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为 .
19.在我国新冠疫情虽然得到了有效的控制,但防范意识仍不能松懈,小丽去药店购买口罩和酒精消毒湿巾,若买150只一次性口罩和10包酒精消毒湿巾,需付75元;若买200只一次性口罩和12包酒精消毒湿巾,需付96元.设一只一次性医用口罩x元,一包酒精消毒湿巾y元,根据题意可列二元一次方程组: .
20.某超市销售时令水果,两次购进一定数量的草莓.已知第一次购买每千克售价是第二次的1.5倍,且第二次购买400千克比第一次购买200千克多花了1000元,求两次购买草莓每千克的售价分别是多少元?若设第一、二次购买草莓每千克的售价分别为x元和y元,根据题意可列方程组为 .
21.如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,列出关于x、y的二元一次方程组 .
22.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”这首诗的意思是说:“如果一间客房住七个人,那么就剩下七个人安排不下;如果一间客房住九个人,那么就空出一间客房.”问,现有客房多少间?房客多少人?设现有客房x间,房客y人,请你列出二元一次方程组: .
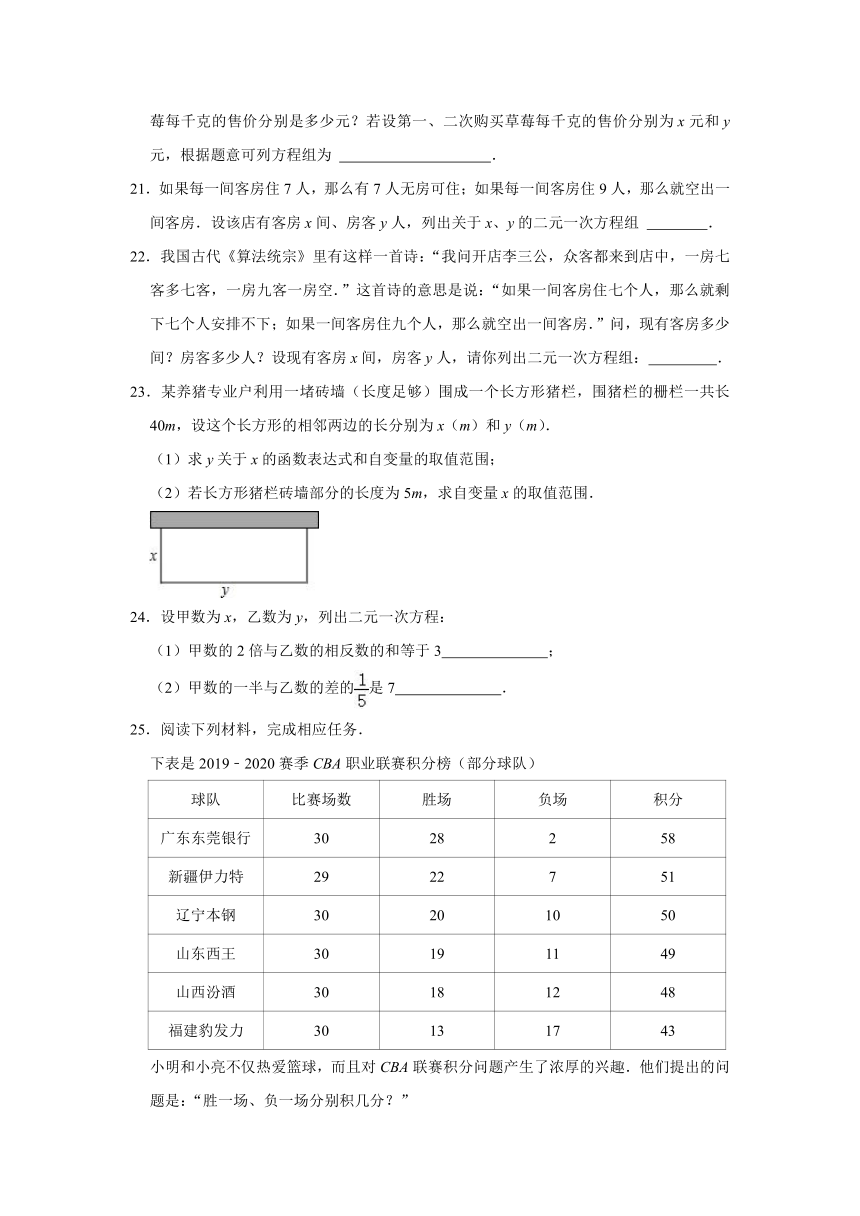
23.某养猪专业户利用一堵砖墙(长度足够)围成一个长方形猪栏,围猪栏的栅栏一共长40m,设这个长方形的相邻两边的长分别为x(m)和y(m).
(1)求y关于x的函数表达式和自变量的取值范围;
(2)若长方形猪栏砖墙部分的长度为5m,求自变量x的取值范围.
24.设甲数为x,乙数为y,列出二元一次方程:
(1)甲数的2倍与乙数的相反数的和等于3 ;
(2)甲数的一半与乙数的差的是7 .
25.阅读下列材料,完成相应任务.
下表是2019﹣2020赛季CBA职业联赛积分榜(部分球队)
球队 比赛场数 胜场 负场 积分
广东东莞银行 30 28 2 58
新疆伊力特 29 22 7 51
辽宁本钢 30 20 10 50
山东西王 30 19 11 49
山西汾酒 30 18 12 48
福建豹发力 30 13 17 43
小明和小亮不仅热爱篮球,而且对CBA联赛积分问题产生了浓厚的兴趣.他们提出的问题是:“胜一场、负一场分别积几分?”
小明的思路是:设胜一场积x分,则根据“广东东莞银行”胜负场数与积分的关系可以用含x的式子表示负一场的积分为 ,再根据“新疆伊力特”胜负场与积分的关系可列一元一次方程 .
小亮的解法是:设胜一场积x分,负一场积y分,…第一步
可得二元一次方程组…第二步
由①,得y=5﹣2x③…第三步
将③代入②,得19x+11(5﹣2x)=49…第四步
解这个方程,得x=2…第五步
将x=2代入③中,得y=1…第六步
解得…第七步
答:胜一场积2分,负一积1分.…第八步
任务1:将小明的思路中的空格处填起来;
任务2:(1)小亮的解法中,列方程①②根据的等量关系分别是:方程① ;方程②: ;
(2)小亮解二元一次方程组的方法叫 ;
(3)小亮的解法中,第四步主要体现的数学思想是 .(选正确选项的代码)
A.转化思想
B.一般到特殊思想
C.分类思想
D.数形结合思想
任务3:设胜一场积x分,负一场积y分,请你选择与小明和小亮不同的等量关系,列二元一次方程组 .(只列不解)
26.小明作业本中有一页被墨水污染了,已知他所列的方程组是正确的,写出题中被墨水污染的条件和第一个方程,并求解这道应用题.
应用题:小东在某商场看中的一台电视和一台空调在“五一”前共需要5500元,由于该商场开展“五一”促销活动,同样的电视打八折销售,于是小东在促销期间购买了同样的电视一台,空调两台,共花费7200元,求“五一”前同样的电视和空调每台各多少元?
解:设“五一”前同样的电视每台x元,空调每台y元,根据题意,得.
被墨水污染的条件是: .
被墨水污染的第一个方程是: .
27.一项调查显示,全世界每天平均有13000人死于与吸烟有关的疾病,我国吸烟者约3.56亿人,占世界吸烟人数的四分之一,比较一年中死于与吸烟有关的疾病的人数占吸烟者总数的百分比,我国比世界其他国家约高0.1%.
根据上述资料,试用二元一次方程组解决以下问题:
我国及世界其他国家一年(按365天计算)中死于与吸烟有关的疾病的人数分别是多少?(只需设出未知数,列出方程组即可)
28.两个两位数的和是68,在较大的两位数的右边接着写较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数.已知前一个四位数比后一个四位数大990.若设较大的两位数为x,较小的两位数为y,回答下列问题:
(1)可得到下列哪一个方程组?
A.;
B.;
C.;
D.;
(2)解所确定的方程组,求这两个两位数.
29.某县在创建省级卫生文明县城中,对县城内的河道进行整治.现有一段长为180米的河道整治任务由甲、乙两个工程队先后接力完成.甲工程队每天整治8米,乙工程队每天整治12米,共用时20天.
(1)小明、小华两位同学提出的解题思路如下:
小明同学:设整治任务完成后甲工程队整治河道x米,乙工程队整治河道y米.
根据题意,得
小华同学:设整治任务完成后,m表示 ,n表示 ;
得
请你补全小明、小华两位同学的解题思路.
(2)求甲、乙两工程队分别整治河道多少米?请从中任选一个方程组求解.(写出完整的解答过程)
30.某校去年有学生1000名,今年比去年增加4.4%,其中寄宿学生增加了6%,走读学生减少了2%,问该校去年有寄宿学生与走读学生各多少名?
参考答案
1.解:设雀每只x两,燕每只y两,则可列出方程组为:
.
故选:B.
2.解:由用一根绳子去量一根长木,绳子还剩余4.5尺,可得方程y=x+4.5,
由将绳子对折再量长木,长木还剩余1尺,可得方程y=x﹣1,
故,
故选:D.
3.解:设该班胜x场,负y场,
依题意得:.
故选:D.
4.解:依题意,得:.
故选:A.
5.解:设他买了x亩好田,y亩坏田,
∵共买好、坏田1顷(1顷=100亩).
∴x+y=100;
∵今有好田1亩,价值300钱;坏田7亩,价值500钱,购买100亩田共花费10000钱,
∴300x+y=10000.
联立两方程组成方程组得:.
故选:B.
6.解:设甲、乙的持钱数分别为x,y,
根据题意可得:,
故选:B.
7.解:设甲需带钱x,乙带钱y,
根据“甲、乙两人各带了若干钱.若甲得到乙所有钱的一半,则甲共有钱50.若乙得到甲所有钱的,则乙也共有钱50”,得,
故选:A.
8.解:设共有y人,x辆车,
依题意得:.
故选:B.
9.解:设甲种型号无人机x架,乙种型号无人机y架,根据题意可列出的方程组是:.
故选:D.
10.解:设甲需持钱x,乙持钱y,
根据题意,得:,
故选:A.
11.解:根据题意可得:
,
故选:A.
12.解:依题意,得:.
故答案为:.
13.解:由题意可得,
图(2)所示的算筹图用方程组表示出来,就是 ,
故答案为:.
14.解:由题意可得,
,
故答案为:.
15.解:依题意,得:.
故答案为:.
16.解:设1头牛值金x两,1只羊值金y两,
由题意可得,,
故答案为:.
17.解:设1台大收割机每小时收割小麦x亩,1台小收割机每小时收割小麦y亩,
由2台大收割机和4台小收割机同时工作2h共收割小麦48亩,可得2(2x+4y)=48,
由3台大收割机和5台小收割机同时工作1h共收割小麦33亩,可得3x+5y=33,
故可得方程组,
故答案为:.
18.解:设有x人,y辆车,根据题意可得:
,
故答案为:.
19.解:依题意得:,
故答案是:.
20.解:若设第一、二次购买草莓每千克的售价分别为x元和y元,
根据题意得到:.
故答案是:.
21.解:设该店有客房x间,房客y人;
根据题意得:,
故答案为:.
22.解:设该店有客房x间,房客y人;
根据题意得:.
故答案是:.
23.解:(1)根据题意可得,2x+y=40,
∴y=40﹣2x.
∴自变量x满足的条件为.
解不等式组得,0<x<20.
∴y关于x的函数表达式为:y=40﹣2x(0<x<20).
(2)由题意可得,40﹣2x≤5,
解得,x≥17.5.
故长方形猪栏砖墙部分的长度为5m,自变量x的取值范围为:17.5≤x<20.
24.解:(1)依题意得:2x+(﹣y)=3.
故答案为:2x+(﹣y)=3.
(2)依题意得:(x﹣y)=7.
故答案为:(x﹣y)=7.
25.解:任务1:设胜一场积x分,则根据“广东东莞银行”胜负场数与积分的关系可以用含x的式子表示负一场的积分为,
根据“新疆伊力特”胜负场与积分的关系可列一元一次方程:,
故答案为:,22x+7×=51;
任务2:(1):(1)小亮的解法中,列方程①②根据的等量关系分别是:方程①辽宁本钢队胜20场积分+负10场积分,共积50分;方程②:山东西王队胜19场积分+负11场积分,共积49分;
故答案为:辽宁本钢队胜20场积分+负10场积分,共积50分;山东西王队胜19场积分+负11场积分,共积49分;
(2)小亮解二元一次方程组的方法叫代入消元法,
故答案为:代入消元法;
(3)小亮的解法中,第四步主要体现的数学思想是转化思想;
故答案为:A;
任务3:设胜一场积x分,负一场积y分,根据“山西汾酒”积分和“福建豹发力”积分可得,.
故答案为:.
26.解:∵设“五一”前同样的电视每台x元,空调每台y元,方程②为0.8x+2(y﹣400)=7200,
∴(y﹣400)表示每台空调在“五一”促销活动中的售价,
∴被墨水污染的条件是:同样的空调每台降价400元.
∵小东在某商场看中的一台电视和一台空调在“五一”前共需要5500元,
∴被墨水污染的第一个方程是:x+y=5500.
故答案为:同样的空调每台降价400元;x+y=5500.
27.解:设我国一年(按365天计算)中死于与吸烟有关的疾病的人数为x人,世界其他国家一年(按365天计算)中死于与吸烟有关的疾病的人数为y人,
根据题意得:.
28.解:设较大的两位数为x,较小的两位数为y,
根据题意,得
,
故选:C;
(2)由(1)知,,
化简得:,
由①+②,得2x=78,即x=39.
由①﹣②,得2y=58,即y=29.
所以这两个数分别是39和29.
29.解:(1)小明、小华两位同学提出的解题思路如下:
小明同学:设整治任务完成后甲工程队整治河道x米,乙工程队整治河道y米.
根据题意得,
小华同学:设整治任务完成后,m表示甲工程队整治河道用的天数,n表示乙工程队整治河道用时的天数;
得;
(2)选小明同学所列方程组解答如下:
,
由②×24得:3x+2y=480③,
由①×2得:2x+2y=360④,
由③﹣④得:x=120,
x=120代入到①得:y=60,
故甲工程队整治河道120米,乙工程队整治河道60米.
30.解:根据某校去年有学生1000名,得方程x+y=1000;
根据今年比去年增加4.4%,其中寄宿学生增加了6%,走读学生减少了2%,得方程为(1+6%)x+(1﹣2%)y=1000×(1+4.4%).
那么方程组可列成:,
解得
答:该校去年有寄宿学生与走读学生分别有800名、200名.
同步达标训练(附答案)
1.《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕,共重16两,雀重燕轻.互换其中一只,恰好一样重.问每只雀、燕的重量各为多少?”解:设雀每只x两,燕每只y两,则可列出方程组为( )
A. B. C. D.
2.《孙子算经》中有一道题,原文是“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺.问木长多少尺?设木长x尺,绳长y尺,可列方程组为( )
A. B. C. D.
3.某校举行篮球赛,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.八年级一班在16场比赛中得26分.设该班胜x场,负y场,则根据题意,下列方程组中正确的是( )
A. B. C. D.
4.我国古代数学著作《九章算术》“盈不足”一章中记载:“今有大器五小器一容三斛,大器一小器五容二斛,问大小器各容几何”.意思是:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛,1个大桶加上5个小桶可以盛酒2斛.问1个大桶、1个小桶分别可以盛酒多少斛?设1个大桶盛酒x斛,1个小桶盛酒y斛,下列方程组正确的是( )
A. B. C. D.
5.《九章算术》“盈不足”一卷中有这样一个问题:“今有善田一亩,价三百;恶田七亩,价五百.今并买一顷,价钱一万.问善、恶田各几何?”意思是:“今有好田1亩,价值300钱;坏田7亩,价值500钱.今共买好、坏田1顷(1顷=100亩),总价值10000钱.问好、坏田各买了多少亩?设好田买了x亩,坏田买了y亩,则下面所列方程组正确的是( )
A.B. C. D.
6.《九章算术》是古代中国第一部自成体系的数学专著,其中《卷第八方程》记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,问甲、乙持钱各几何?”译文是:今有甲、乙两人持钱不知道各有多少,甲若得到乙所有钱的,则甲有50钱,乙若得到甲所有钱的,则乙也有50钱.问甲、乙各持钱多少?设甲持钱数为x钱,乙持钱数为y钱,列出关于x、y的二元一次方程组是( )
A. B.
C. D.
7.《九章算术》中记载了一个问题,大意是甲、乙两人各带了若干钱.若甲得到乙所有钱的一半,则甲共有钱50.若乙得到甲所有钱的,则乙也共有钱50.甲、乙两人各带了多少钱?设甲带了钱x,乙带了钱y,依题意,下面所列方程组正确的是( )
A. B.
C. D.
8.《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步.问:人与车各几何?译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行,问:人与车各多少?设有x辆车,人数为y,根据题意可列方程组为( )
A. B.
C. D.
9.某公司上半年生产甲、乙两种型号的无人机若干架,已知甲种型号无人机架数比总架数的一半多11架,乙种型号无人机架数比总架数的三分之一少2架.设甲种型号无人机x架,乙种型号无人机y架,根据题意可列出的方程组是( )
A. B.
C. D.
10.《九章算术》卷八方程第十题原文为:“今有甲、乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而亦钱五十.问:甲、乙持钱各几何?”题目大意是:甲、乙两人各带了若干钱.如果甲得到乙所有钱的一半,那么甲共有钱50;如果乙得到甲所有钱的,那么乙也共有钱50.问:甲、乙两人各带了多少钱?设甲、乙两人持钱的数量分别为x,y,则可列方程组为( )
A.B.C.D.
11.中国古代人民在生产生活中发现了许多数学问题,在《孙子算经》中记载了这样一个问题,大意为:有若干人乘车,若每车乘坐3人,则2辆车无人乘坐;若每车乘坐2人,则9人无车可乘,问共有多少辆车,多少人,设共有x辆车,y人,则可列方程组为( )
A.B. C.D.
12.我国古代数学名著《九章算术》上有这样一个问题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”其大意是:今有醇酒(优质酒)1斗,价值50钱;行酒(劣质酒)1斗,价值10钱.现用30钱,买得2斗酒.问醇酒、行酒各能买得多少?设醇酒为x斗,行酒为y斗,根据题意,可列方程组为 .
13.《九章算术》是我国东汉初年编订的一部数学经典著作,其中一次方程组是用算筹布置而成,如图(1)所示的算筹图用我们现在所熟悉的方程组表示出来,就是,类似的,图(2)所示的算筹图用方程组表示出来,就是 .
14.《九章算术》记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?”其大意是:“今有甲乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的钱数为50;而甲把其的钱给乙,则乙的钱数也为50.问甲、乙各有多少钱?”设甲的钱数为x,乙的钱数为y,根据题意,可列方程组为 .
15.《孙子算经》记载:今有3人共车,二车空;二人共车,九人步,问人与车各几何?译文:今有若干人乘车,若每三人共乘一辆车,最终剩余2辆车;若每2人共乘一辆车,最终剩余9人无车可乘.问共有多少人?多少辆车?若设有x人,y辆车,则可列方程组为 .
16.《九章算术》是我国古代一部著名的算书,它的出现标志着中国古代数学形成了完整的体系.其中卷八方程[七]中记载:“今有牛五、羊二,直金十两.牛二、羊五,直金八两.牛、羊各直金几何?”题目大意是:5头牛、2只羊共值金10两.2头牛、5只羊共值金8两.每头牛、每只羊各值金多少两?设1头牛值金x两,1只羊值金y两,则可列方程组为 .
17.山西省小麦种植面积在1000万亩以上,端午前后是小麦收割的季节.2台大收割机和4台小收割机同时工作2h共收割小麦48亩,3台大收割机和5台小收割机同时工作1h共收割小麦33亩.1台大收割机和1台小收割机每小时各收割小麦多少亩?设1台大收割机每小时收割小麦x亩,1台小收割机每小时收割小麦y亩,则根据题意可列方程组 .
18.《孙于算经》是中国古代重要的数学著作,其中一道题的原文是:“今三人共车,两车空;二人共车,九人步,问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为 .
19.在我国新冠疫情虽然得到了有效的控制,但防范意识仍不能松懈,小丽去药店购买口罩和酒精消毒湿巾,若买150只一次性口罩和10包酒精消毒湿巾,需付75元;若买200只一次性口罩和12包酒精消毒湿巾,需付96元.设一只一次性医用口罩x元,一包酒精消毒湿巾y元,根据题意可列二元一次方程组: .
20.某超市销售时令水果,两次购进一定数量的草莓.已知第一次购买每千克售价是第二次的1.5倍,且第二次购买400千克比第一次购买200千克多花了1000元,求两次购买草莓每千克的售价分别是多少元?若设第一、二次购买草莓每千克的售价分别为x元和y元,根据题意可列方程组为 .
21.如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,列出关于x、y的二元一次方程组 .
22.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”这首诗的意思是说:“如果一间客房住七个人,那么就剩下七个人安排不下;如果一间客房住九个人,那么就空出一间客房.”问,现有客房多少间?房客多少人?设现有客房x间,房客y人,请你列出二元一次方程组: .
23.某养猪专业户利用一堵砖墙(长度足够)围成一个长方形猪栏,围猪栏的栅栏一共长40m,设这个长方形的相邻两边的长分别为x(m)和y(m).
(1)求y关于x的函数表达式和自变量的取值范围;
(2)若长方形猪栏砖墙部分的长度为5m,求自变量x的取值范围.
24.设甲数为x,乙数为y,列出二元一次方程:
(1)甲数的2倍与乙数的相反数的和等于3 ;
(2)甲数的一半与乙数的差的是7 .
25.阅读下列材料,完成相应任务.
下表是2019﹣2020赛季CBA职业联赛积分榜(部分球队)
球队 比赛场数 胜场 负场 积分
广东东莞银行 30 28 2 58
新疆伊力特 29 22 7 51
辽宁本钢 30 20 10 50
山东西王 30 19 11 49
山西汾酒 30 18 12 48
福建豹发力 30 13 17 43
小明和小亮不仅热爱篮球,而且对CBA联赛积分问题产生了浓厚的兴趣.他们提出的问题是:“胜一场、负一场分别积几分?”
小明的思路是:设胜一场积x分,则根据“广东东莞银行”胜负场数与积分的关系可以用含x的式子表示负一场的积分为 ,再根据“新疆伊力特”胜负场与积分的关系可列一元一次方程 .
小亮的解法是:设胜一场积x分,负一场积y分,…第一步
可得二元一次方程组…第二步
由①,得y=5﹣2x③…第三步
将③代入②,得19x+11(5﹣2x)=49…第四步
解这个方程,得x=2…第五步
将x=2代入③中,得y=1…第六步
解得…第七步
答:胜一场积2分,负一积1分.…第八步
任务1:将小明的思路中的空格处填起来;
任务2:(1)小亮的解法中,列方程①②根据的等量关系分别是:方程① ;方程②: ;
(2)小亮解二元一次方程组的方法叫 ;
(3)小亮的解法中,第四步主要体现的数学思想是 .(选正确选项的代码)
A.转化思想
B.一般到特殊思想
C.分类思想
D.数形结合思想
任务3:设胜一场积x分,负一场积y分,请你选择与小明和小亮不同的等量关系,列二元一次方程组 .(只列不解)
26.小明作业本中有一页被墨水污染了,已知他所列的方程组是正确的,写出题中被墨水污染的条件和第一个方程,并求解这道应用题.
应用题:小东在某商场看中的一台电视和一台空调在“五一”前共需要5500元,由于该商场开展“五一”促销活动,同样的电视打八折销售,于是小东在促销期间购买了同样的电视一台,空调两台,共花费7200元,求“五一”前同样的电视和空调每台各多少元?
解:设“五一”前同样的电视每台x元,空调每台y元,根据题意,得.
被墨水污染的条件是: .
被墨水污染的第一个方程是: .
27.一项调查显示,全世界每天平均有13000人死于与吸烟有关的疾病,我国吸烟者约3.56亿人,占世界吸烟人数的四分之一,比较一年中死于与吸烟有关的疾病的人数占吸烟者总数的百分比,我国比世界其他国家约高0.1%.
根据上述资料,试用二元一次方程组解决以下问题:
我国及世界其他国家一年(按365天计算)中死于与吸烟有关的疾病的人数分别是多少?(只需设出未知数,列出方程组即可)
28.两个两位数的和是68,在较大的两位数的右边接着写较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数.已知前一个四位数比后一个四位数大990.若设较大的两位数为x,较小的两位数为y,回答下列问题:
(1)可得到下列哪一个方程组?
A.;
B.;
C.;
D.;
(2)解所确定的方程组,求这两个两位数.
29.某县在创建省级卫生文明县城中,对县城内的河道进行整治.现有一段长为180米的河道整治任务由甲、乙两个工程队先后接力完成.甲工程队每天整治8米,乙工程队每天整治12米,共用时20天.
(1)小明、小华两位同学提出的解题思路如下:
小明同学:设整治任务完成后甲工程队整治河道x米,乙工程队整治河道y米.
根据题意,得
小华同学:设整治任务完成后,m表示 ,n表示 ;
得
请你补全小明、小华两位同学的解题思路.
(2)求甲、乙两工程队分别整治河道多少米?请从中任选一个方程组求解.(写出完整的解答过程)
30.某校去年有学生1000名,今年比去年增加4.4%,其中寄宿学生增加了6%,走读学生减少了2%,问该校去年有寄宿学生与走读学生各多少名?
参考答案
1.解:设雀每只x两,燕每只y两,则可列出方程组为:
.
故选:B.
2.解:由用一根绳子去量一根长木,绳子还剩余4.5尺,可得方程y=x+4.5,
由将绳子对折再量长木,长木还剩余1尺,可得方程y=x﹣1,
故,
故选:D.
3.解:设该班胜x场,负y场,
依题意得:.
故选:D.
4.解:依题意,得:.
故选:A.
5.解:设他买了x亩好田,y亩坏田,
∵共买好、坏田1顷(1顷=100亩).
∴x+y=100;
∵今有好田1亩,价值300钱;坏田7亩,价值500钱,购买100亩田共花费10000钱,
∴300x+y=10000.
联立两方程组成方程组得:.
故选:B.
6.解:设甲、乙的持钱数分别为x,y,
根据题意可得:,
故选:B.
7.解:设甲需带钱x,乙带钱y,
根据“甲、乙两人各带了若干钱.若甲得到乙所有钱的一半,则甲共有钱50.若乙得到甲所有钱的,则乙也共有钱50”,得,
故选:A.
8.解:设共有y人,x辆车,
依题意得:.
故选:B.
9.解:设甲种型号无人机x架,乙种型号无人机y架,根据题意可列出的方程组是:.
故选:D.
10.解:设甲需持钱x,乙持钱y,
根据题意,得:,
故选:A.
11.解:根据题意可得:
,
故选:A.
12.解:依题意,得:.
故答案为:.
13.解:由题意可得,
图(2)所示的算筹图用方程组表示出来,就是 ,
故答案为:.
14.解:由题意可得,
,
故答案为:.
15.解:依题意,得:.
故答案为:.
16.解:设1头牛值金x两,1只羊值金y两,
由题意可得,,
故答案为:.
17.解:设1台大收割机每小时收割小麦x亩,1台小收割机每小时收割小麦y亩,
由2台大收割机和4台小收割机同时工作2h共收割小麦48亩,可得2(2x+4y)=48,
由3台大收割机和5台小收割机同时工作1h共收割小麦33亩,可得3x+5y=33,
故可得方程组,
故答案为:.
18.解:设有x人,y辆车,根据题意可得:
,
故答案为:.
19.解:依题意得:,
故答案是:.
20.解:若设第一、二次购买草莓每千克的售价分别为x元和y元,
根据题意得到:.
故答案是:.
21.解:设该店有客房x间,房客y人;
根据题意得:,
故答案为:.
22.解:设该店有客房x间,房客y人;
根据题意得:.
故答案是:.
23.解:(1)根据题意可得,2x+y=40,
∴y=40﹣2x.
∴自变量x满足的条件为.
解不等式组得,0<x<20.
∴y关于x的函数表达式为:y=40﹣2x(0<x<20).
(2)由题意可得,40﹣2x≤5,
解得,x≥17.5.
故长方形猪栏砖墙部分的长度为5m,自变量x的取值范围为:17.5≤x<20.
24.解:(1)依题意得:2x+(﹣y)=3.
故答案为:2x+(﹣y)=3.
(2)依题意得:(x﹣y)=7.
故答案为:(x﹣y)=7.
25.解:任务1:设胜一场积x分,则根据“广东东莞银行”胜负场数与积分的关系可以用含x的式子表示负一场的积分为,
根据“新疆伊力特”胜负场与积分的关系可列一元一次方程:,
故答案为:,22x+7×=51;
任务2:(1):(1)小亮的解法中,列方程①②根据的等量关系分别是:方程①辽宁本钢队胜20场积分+负10场积分,共积50分;方程②:山东西王队胜19场积分+负11场积分,共积49分;
故答案为:辽宁本钢队胜20场积分+负10场积分,共积50分;山东西王队胜19场积分+负11场积分,共积49分;
(2)小亮解二元一次方程组的方法叫代入消元法,
故答案为:代入消元法;
(3)小亮的解法中,第四步主要体现的数学思想是转化思想;
故答案为:A;
任务3:设胜一场积x分,负一场积y分,根据“山西汾酒”积分和“福建豹发力”积分可得,.
故答案为:.
26.解:∵设“五一”前同样的电视每台x元,空调每台y元,方程②为0.8x+2(y﹣400)=7200,
∴(y﹣400)表示每台空调在“五一”促销活动中的售价,
∴被墨水污染的条件是:同样的空调每台降价400元.
∵小东在某商场看中的一台电视和一台空调在“五一”前共需要5500元,
∴被墨水污染的第一个方程是:x+y=5500.
故答案为:同样的空调每台降价400元;x+y=5500.
27.解:设我国一年(按365天计算)中死于与吸烟有关的疾病的人数为x人,世界其他国家一年(按365天计算)中死于与吸烟有关的疾病的人数为y人,
根据题意得:.
28.解:设较大的两位数为x,较小的两位数为y,
根据题意,得
,
故选:C;
(2)由(1)知,,
化简得:,
由①+②,得2x=78,即x=39.
由①﹣②,得2y=58,即y=29.
所以这两个数分别是39和29.
29.解:(1)小明、小华两位同学提出的解题思路如下:
小明同学:设整治任务完成后甲工程队整治河道x米,乙工程队整治河道y米.
根据题意得,
小华同学:设整治任务完成后,m表示甲工程队整治河道用的天数,n表示乙工程队整治河道用时的天数;
得;
(2)选小明同学所列方程组解答如下:
,
由②×24得:3x+2y=480③,
由①×2得:2x+2y=360④,
由③﹣④得:x=120,
x=120代入到①得:y=60,
故甲工程队整治河道120米,乙工程队整治河道60米.
30.解:根据某校去年有学生1000名,得方程x+y=1000;
根据今年比去年增加4.4%,其中寄宿学生增加了6%,走读学生减少了2%,得方程为(1+6%)x+(1﹣2%)y=1000×(1+4.4%).
那么方程组可列成:,
解得
答:该校去年有寄宿学生与走读学生分别有800名、200名.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
