二次函数复习课
图片预览




文档简介
(共28张PPT)
二次函数复习课(第一课时)
美丽的彩虹
一、二次函数的概念
一般地,如果 ,那么y叫做x 的二次函数.
y=ax2+bx+c(a,b,c是常数,a≠0)
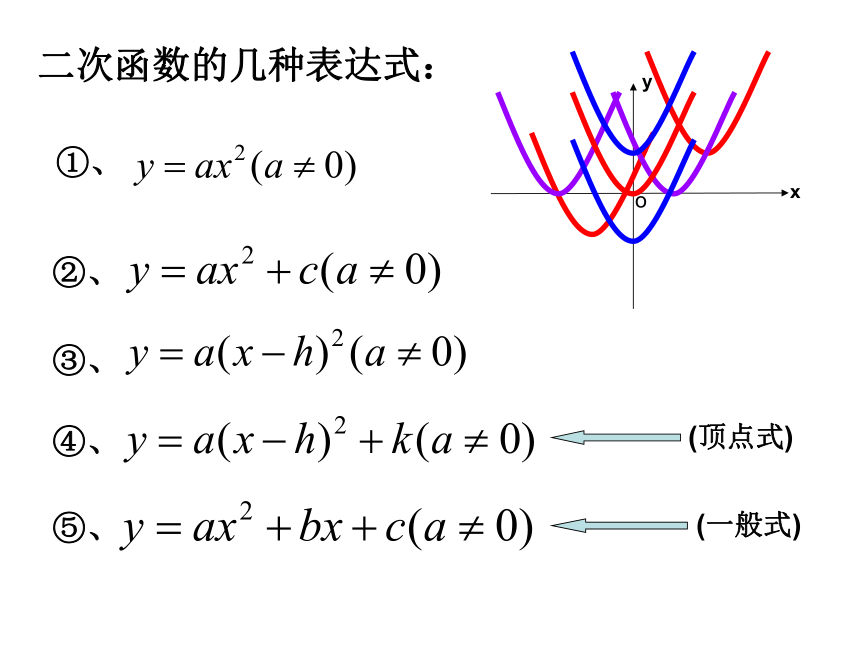
二次函数的几种表达式:
①、
②、
③、
④、
⑤、
(顶点式)
(一般式)
x
y
o
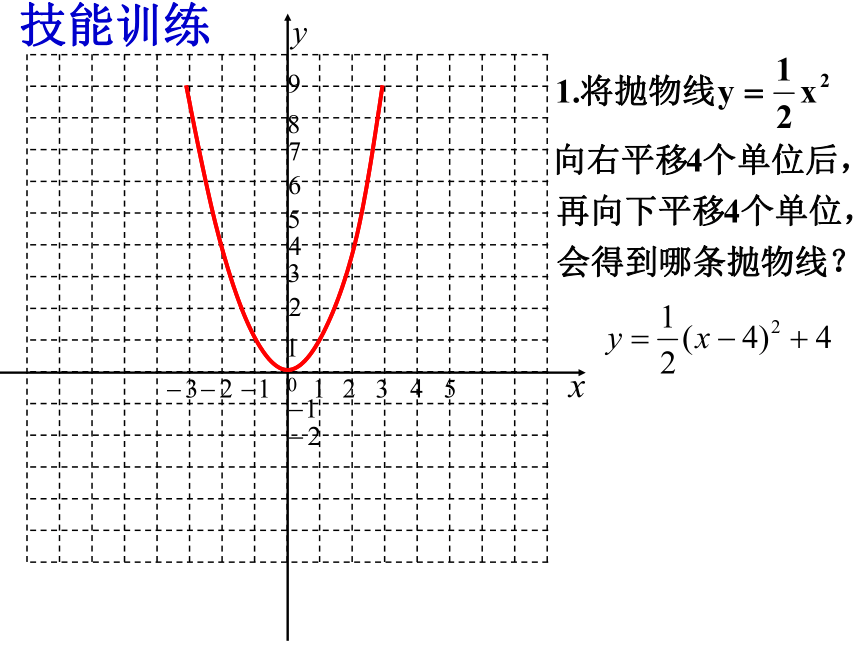
技能训练
2、已知抛物线的图象经过A(1,0),B(-1,6) ,C (3,2)三点的抛物线解析为 .
技能训练
y=x2-3x+2
3、已知抛物线的顶点坐标为 ( -2,3) ,并且过(-1,4) ,可得抛物线解析式为
y=(x+2)2+3
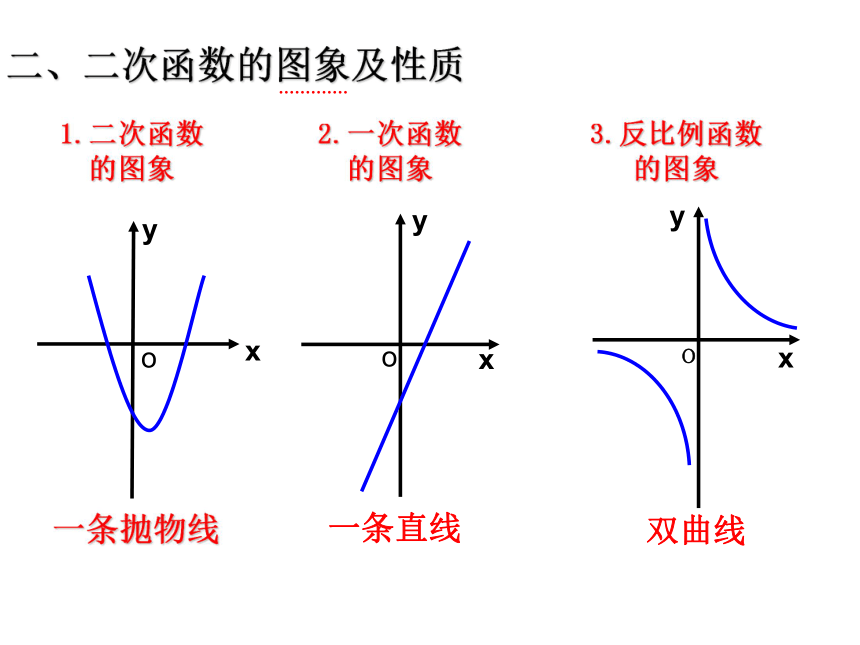
二、二次函数的图象及性质
2.一次函数的图象
一条直线
o
x
y
x
y
1.二次函数的图象
一条抛物线
o
3.反比例函数的图象
双曲线
O
y
x
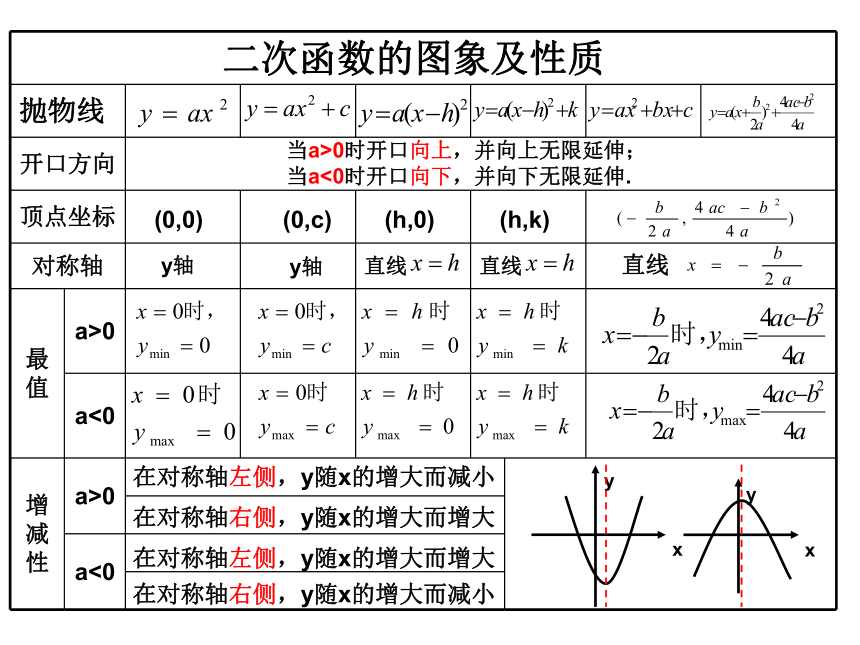
抛物线
开口方向
顶点坐标
对称轴
最值 a>0
a<0
增减性 a>0
a<0
二次函数的图象及性质
当a>0时开口向上,并向上无限延伸;
当a<0时开口向下,并向下无限延伸.
(0,0)
(0,c)
(h,0)
(h,k)
直线
y轴
直线
直线
在对称轴左侧,y随x的增大而减小
在对称轴右侧,y随x的增大而增大
在对称轴左侧,y随x的增大而增大
在对称轴右侧,y随x的增大而减小
x
y
x
y
y轴
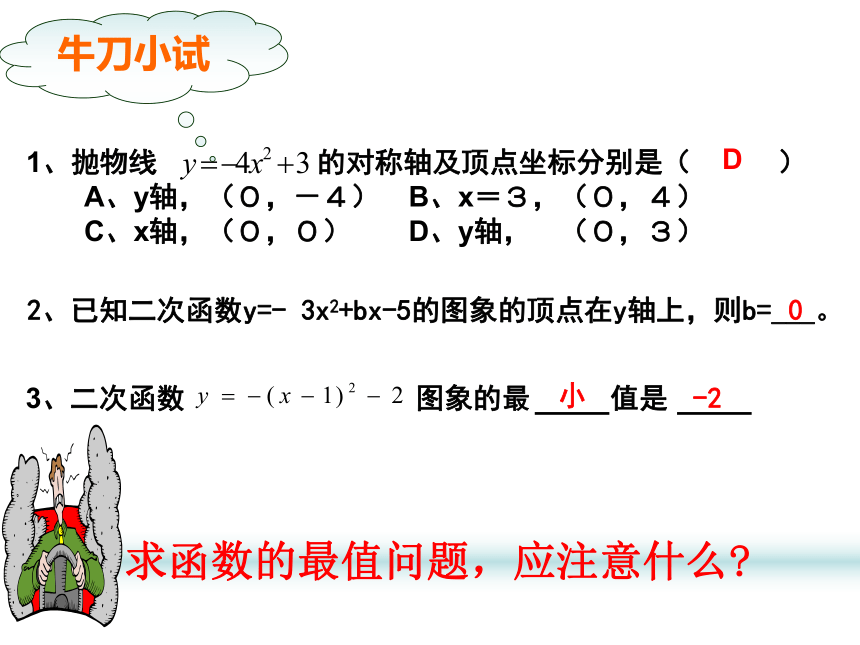
1、抛物线 的对称轴及顶点坐标分别是( )
A、y轴,(0,-4) B、x=3,(0,4)
C、x轴,(0,0) D、y轴, (0,3)
D
牛刀小试
3、二次函数 图象的最 值是
小
-2
求函数的最值问题,应注意什么
2、已知二次函数y=- 3x2+bx-5的图象的顶点在y轴上,则b=___。
0
三、二次函数y=ax2+bx+c(a≠0)的系数a,b,c,△与
抛物线的关系
a
a,b
c
△
a决定开口方向:
a,b同时决定对称轴位置:
c决定抛物线与y轴的交点:
△决定抛物线与x轴的交点:
a>0时开口向上
a<0时开口向下
a、b同号时对称轴在y轴左侧
a、b异号时对称轴在y轴右侧
b=0时对称轴是y轴(左同右异)
c>0时抛物线交于y轴的正半轴
c=0时抛物线过原点
c<0时抛物线交于y轴的负半轴
△>0时抛物线与x轴有两个交点
△=0时抛物线与x轴有一个交点
△<0时抛物线于x轴没有交点
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
o
y
开口向上a>0
左同右异 b<0
抛物线交于y轴的正半轴c>0
抛物线与x轴有两个交点△>0
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
o
y
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线与x轴有两个交点△>0
抛物线抛物线过原点c=0
左同右异 b>0
开口向上a>0
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
例1:
已知二次函数
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(5)x为何值时,y<0?x为何值时,y>0?
M(-1,-2)
∴
例1:
已知二次函数
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(5)x为何值时,y<0?x为何值时,y>0?
∴c(0,-1.5)
解:当x=0时代入 得y=-1.5
当y=0时代入 得
∴A(1,0),B(-3,0)
∴x1=1,x2=-3
例1:
已知二次函数
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(5)x为何值时,y<0?x为何值时,y>0?
解:(3)
0
x
y
①画对称轴
x=-1
②确定顶点
(-1,-2)
④连线
③确定与坐标轴的交点
及对称点
(-3,0)
(1,0)
例1:
解:(4)
0
当x=-1时,y有最小值为
y=-2
当x<-1时,y随x的增大
而减小;
已知二次函数
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(5)x为何值时,y<0?x为何值时,y>0?
1
-1
x
x=-1
y
-3
解:(5)
0
(-1,-2)
(0,-–)
(-3,0)
(1,0)
3
2
y
x
由图象可知
当x< -3或x>1时,y > 0
例1:
已知二次函数
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(5)x为何值时,y<0?x为何值时,y>0?
当-3 < x < 1时, y < 0
抛物线y=ax2+bx+c(a≠0)的图象
经过原点和二、三、四象限,判断
a、b、c的符号情况:
a 0,b 0,c 0.
<
<
=
x
y
o
点燃思维
1、二次函数的概念
2、二次函数的图象及性质
3、二次函数y=ax2+bx+c(a≠0)的系数a, b,c,△与抛物线的关系.
解决这类问题的关键是运用数形结合思想,即会观察图象;如遇到2a+b,2a-b要与对称轴联系等;
请你倾听我的收获……
4、会合理选择二次函数的解析式
资料P51基础练习1~10小题
二次函数复习课(第一课时)
美丽的彩虹
一、二次函数的概念
一般地,如果 ,那么y叫做x 的二次函数.
y=ax2+bx+c(a,b,c是常数,a≠0)
二次函数的几种表达式:
①、
②、
③、
④、
⑤、
(顶点式)
(一般式)
x
y
o
技能训练
2、已知抛物线的图象经过A(1,0),B(-1,6) ,C (3,2)三点的抛物线解析为 .
技能训练
y=x2-3x+2
3、已知抛物线的顶点坐标为 ( -2,3) ,并且过(-1,4) ,可得抛物线解析式为
y=(x+2)2+3
二、二次函数的图象及性质
2.一次函数的图象
一条直线
o
x
y
x
y
1.二次函数的图象
一条抛物线
o
3.反比例函数的图象
双曲线
O
y
x
抛物线
开口方向
顶点坐标
对称轴
最值 a>0
a<0
增减性 a>0
a<0
二次函数的图象及性质
当a>0时开口向上,并向上无限延伸;
当a<0时开口向下,并向下无限延伸.
(0,0)
(0,c)
(h,0)
(h,k)
直线
y轴
直线
直线
在对称轴左侧,y随x的增大而减小
在对称轴右侧,y随x的增大而增大
在对称轴左侧,y随x的增大而增大
在对称轴右侧,y随x的增大而减小
x
y
x
y
y轴
1、抛物线 的对称轴及顶点坐标分别是( )
A、y轴,(0,-4) B、x=3,(0,4)
C、x轴,(0,0) D、y轴, (0,3)
D
牛刀小试
3、二次函数 图象的最 值是
小
-2
求函数的最值问题,应注意什么
2、已知二次函数y=- 3x2+bx-5的图象的顶点在y轴上,则b=___。
0
三、二次函数y=ax2+bx+c(a≠0)的系数a,b,c,△与
抛物线的关系
a
a,b
c
△
a决定开口方向:
a,b同时决定对称轴位置:
c决定抛物线与y轴的交点:
△决定抛物线与x轴的交点:
a>0时开口向上
a<0时开口向下
a、b同号时对称轴在y轴左侧
a、b异号时对称轴在y轴右侧
b=0时对称轴是y轴(左同右异)
c>0时抛物线交于y轴的正半轴
c=0时抛物线过原点
c<0时抛物线交于y轴的负半轴
△>0时抛物线与x轴有两个交点
△=0时抛物线与x轴有一个交点
△<0时抛物线于x轴没有交点
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
o
y
开口向上a>0
左同右异 b<0
抛物线交于y轴的正半轴c>0
抛物线与x轴有两个交点△>0
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
o
y
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线与x轴有两个交点△>0
抛物线抛物线过原点c=0
左同右异 b>0
开口向上a>0
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
例1:
已知二次函数
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(5)x为何值时,y<0?x为何值时,y>0?
M(-1,-2)
∴
例1:
已知二次函数
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(5)x为何值时,y<0?x为何值时,y>0?
∴c(0,-1.5)
解:当x=0时代入 得y=-1.5
当y=0时代入 得
∴A(1,0),B(-3,0)
∴x1=1,x2=-3
例1:
已知二次函数
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(5)x为何值时,y<0?x为何值时,y>0?
解:(3)
0
x
y
①画对称轴
x=-1
②确定顶点
(-1,-2)
④连线
③确定与坐标轴的交点
及对称点
(-3,0)
(1,0)
例1:
解:(4)
0
当x=-1时,y有最小值为
y=-2
当x<-1时,y随x的增大
而减小;
已知二次函数
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(5)x为何值时,y<0?x为何值时,y>0?
1
-1
x
x=-1
y
-3
解:(5)
0
(-1,-2)
(0,-–)
(-3,0)
(1,0)
3
2
y
x
由图象可知
当x< -3或x>1时,y > 0
例1:
已知二次函数
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(5)x为何值时,y<0?x为何值时,y>0?
当-3 < x < 1时, y < 0
抛物线y=ax2+bx+c(a≠0)的图象
经过原点和二、三、四象限,判断
a、b、c的符号情况:
a 0,b 0,c 0.
<
<
=
x
y
o
点燃思维
1、二次函数的概念
2、二次函数的图象及性质
3、二次函数y=ax2+bx+c(a≠0)的系数a, b,c,△与抛物线的关系.
解决这类问题的关键是运用数形结合思想,即会观察图象;如遇到2a+b,2a-b要与对称轴联系等;
请你倾听我的收获……
4、会合理选择二次函数的解析式
资料P51基础练习1~10小题
