特殊四边形复习4课时

第一章 特 殊 四 边 形 复 习（2课时）
总第 课时 设计人：谢伟
学习目标：
1、熟练掌握特殊四边形的性质和判定，并能应用其解决相关问题。
2、了解厂家的辅助线，并能够尝试添加辅助线，帮助解决问题。
3、熟练运用综合法证明几何问题，同时建立空间观念，发展学生机和直观与推理能力。
学习重难点：
1、熟练掌握特殊四边形的性质和判定，并能应用其解决相关问题。
2、尝试添加辅助线，帮助解决问题。
学习过程：
一、课前预习
任务：基础知识复习
1. 平行四边形的性质
（1）平行四边形对边___ ___，对角___ ___；角平分线___ ___；邻角___ ___.
（2）平行四边形两个邻角的平分线互相______，两个对角的平分线互相______（ “平行”、“垂直”）
（3）平行四边形的面积公式________ ____________.
2．平行四边形的判定
（1）定义：__________ ______________.
（2）边：_________________ _______或_____________ __________．
（3）角：__________ ______________．
（4）对角线：_____________ ___________．
3. 特殊的平行四边形的性质
边 角 对角线 对称性
矩形
菱形
正方形
4．特殊的平行四边形的判别方法
（1）菱形的判定：①．__________________边都相等的四边形菱形．
②．对角线_____________________________的平行四边形是菱形．
③．对角线_____________________________________________的四边形是菱形．
（2）矩形的判定：①．有_____个是直角的四边形是矩形．
②．对角线____________________________的平行四边形是矩形．
③．对角线________________________________的四边形是矩形．
（3）正方形的判定：先判定这个四边形是矩形，再判定这个矩形还是_____形；
或者先判定四边形是菱形，再判定这个菱形也是_____形．
5．等腰梯形的性质：边 ______________________________ ____.
角 _______ ___________________________.
对角线 _________ _________________________.
6.等腰梯形的判别方法
（1）定义：__________ ______________.
（2）角：_________________ ___________________ __________．
（3）对角线：__________ ______________．
预习诊断：1、一个菱形的两条对角线分别是6cm，8cm，则这个菱形的周长等于 cm，
面积是 cm2
2、如图，矩形ABCD的两条对角线相交于O，∠AOD=120°，AB=4cm，则矩形对角线AC长为______cm．
3、如图，在正方形ABCD的外侧，作等边三角形ADE，则∠AEBO （ ）
A. 10° B．15° C．20° D．12.5°
4、如图，梯形ABCD中，AD∥BC，∠B=60°，∠C=30°，AD=2，BC=8.梯形的腰AB= ，
CD= .
二、合作探究
1、如图：AE∥BF，AC平分∠BAD，且交BF于点C，BD平分∠ABC，且交AE于点D，连接CD，
求证：四边形ABCD是菱形
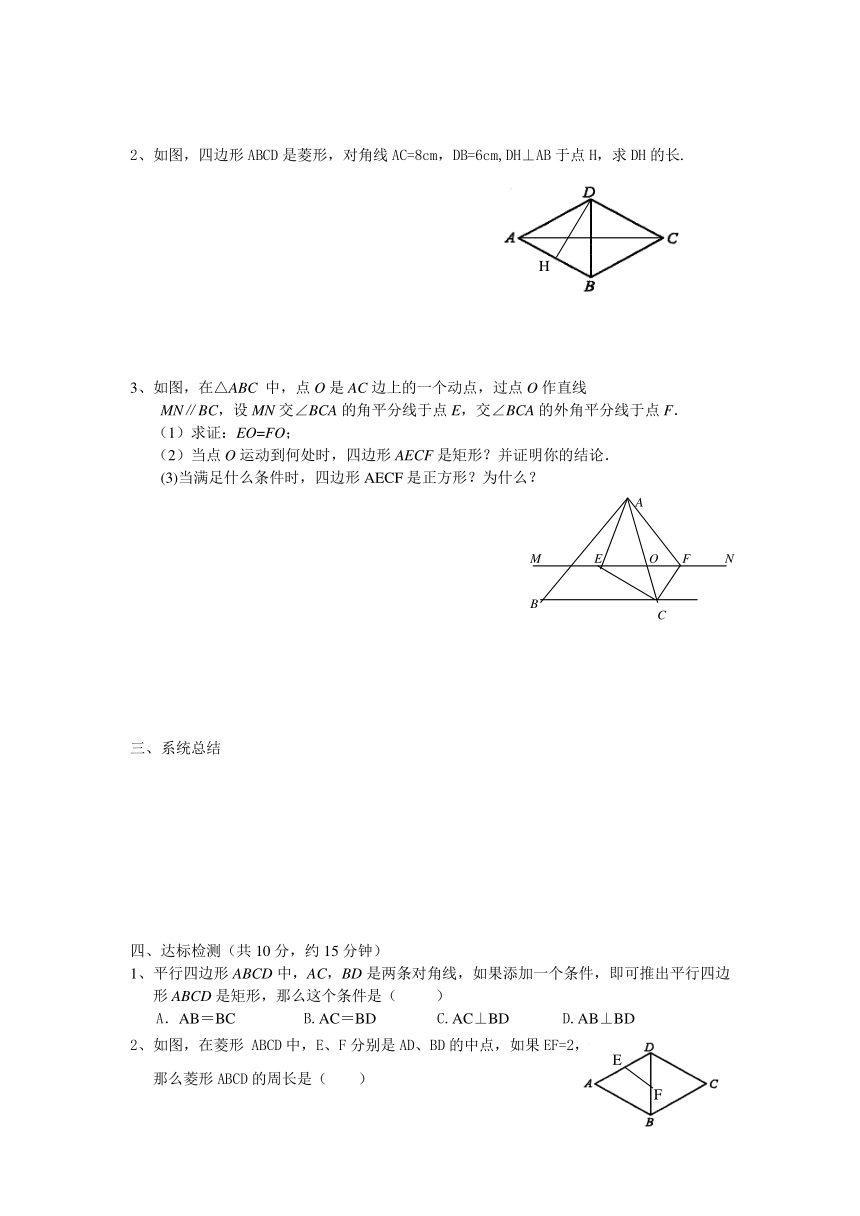
2、如图，四边形ABCD是菱形，对角线AC=8cm，DB=6cm,DH⊥AB于点H，求DH的长.
3、如图，在△ABC 中，点O是AC边上的一个动点，过点O作直线
MN∥BC，设MN交∠BCA的角平分线于点E，交∠BCA的外角平分线于点F．
（1）求证：EO=FO；
（2）当点O运动到何处时，四边形AECF是矩形？并证明你的结论．
(3)当满足什么条件时，四边形AECF是正方形？为什么？
三、系统总结
四、达标检测（共10分，约15分钟）
1、平行四边形ABCD中，AC，BD是两条对角线，如果添加一个条件，即可推出平行四边形ABCD是矩形，那么这个条件是（ ）
A．AB＝BC B.AC＝BD C.AC⊥BD D.AB⊥BD
2、如图，在菱形 ABCD中，E、F分别是AD、BD的中点，如果EF=2，
那么菱形ABCD的周长是（ ）
A. 4 B．8 C．12 D．16
3、四边形ABCD中，若∠A︰∠B︰∠C︰∠D＝2︰2︰1︰3，那么这个四边形是（ ）
　 A．梯形 B．等腰梯形 C．直角梯形 D．任意四边形
4、如图，把矩形沿对折后使两部分重合，若，
则=（ ）
A．110° B．115° C．120° D．130°
5、如图，在梯形ABCD中，上底AD＝1 cm，下底BC＝4cm，对角线BD⊥AC，
且BD＝3cm，AC＝4cm．求梯形ABCD的面积．
第一章特殊四边形复习课（2课时）
总第 课时 设计人：谢伟
【基础知识复习】
1、平行四边形
（1）性质：
边：对边平行且相等。 AB=CD AB∥CD
BC=AD BC∥AD
角：对角相等，邻角互补。∠A=∠C ∠A+∠B=180°
∠B=∠D ∠C+∠D=180°
对角线：对角线互相平分。 A0=CO BO=DO
（2）判别方法：
a、两组对边分别平行的四边形是平行四边形。
b、两组对边分别相等的四边形是平行四边形。
c、一组对边平行且相等的四边形是平行四边形。
或
d、两组对角分别相等的四边形是平行四边形。
e、两条对角线互相平分的四边形是平行四边形。
2、菱形 （1）性质
边：四条边都相等。 AB=CD =BC=AD
对角线：对角线互相垂直平分，且每条对角线平分一组对角。
AC⊥BD ； A0=CO ， BO=DO ；
AC平分∠DAB和∠DCB； BD平分∠ADC和∠ABC
（2）判别方法：
a、一组邻边相等的平行四边形是菱形。（菱形的定义）
b、对角线互相垂直的平行四边形是菱形。
（对角线互相垂直平分的四边形是菱形）
c、四条边都相等的四边形是菱形。
3、矩形 （1）性质：
角：四个角都相等。∠A=∠B=∠C=∠D=90°
对角线：对角线相等且平分。AC=BD A0=CO BO=DO
直角三角形中斜边上的中线等于斜边的一半。
（2）判别方法：
a、有一个角是直角的平行四边形是矩形。
b、对角线相等的平行四边形是矩形。
（对角线相等且平分的四边形是矩形）
c、有三个角是直角的四边形是矩形。
4、正方形
（1）性质：具有平行四边形、菱形、矩形的所有性质。
（2）判别方法：
思路一：先判断它是菱形，再判断它是矩形。
思路二：先判断它是矩形，再判断它是菱形。
a、有一个角是直角的菱形是正方形。
b、对角线相等的菱形是正方形。
c、有一组邻边相等的矩形是正方形。
d、对角线互相垂直的矩形是正方形。
由b、d可以转换一种表述形式：对角线相等、垂直且平分的四边形是正方形。
5、等腰梯形
（1）性质：
边：上下底边平行，两腰相等。
AD∥BC AB＝CD
角：同一底边的两个底角相等，邻角互补。
∠A＝∠D；∠B＝∠C；∠A＋∠B＝180°；∠C＋∠D＝180°
对角线：对角线相等。 AC＝BD
（2）判别方法：
a、两腰相等的梯形是等腰梯形。
b、同一底上两个底角相等的梯形是等腰梯形。
或
c、对角线相等的梯形是等腰梯形。
6、中心对称图形
概念：将一个图形绕着某个点旋转180°后，能和原来的图形重合，这样的图形叫中心对称图形。
常见的中心对称图形：平行四边形、菱形、矩形、正方形、圆、线段等。
（补充）常见的轴对称：等腰三角形、等边三角形、菱形、矩形、正方形、等腰梯形、圆、线段、角等。
A
B
C
D
E
A
B
C
D
A
B
C
D
O
E
F
H
A
B
C
E
F
M
N
O
E
F