直线与平面,平面与平面的位置关系
文档属性
| 名称 | 直线与平面,平面与平面的位置关系 |  | |
| 格式 | zip | ||
| 文件大小 | 378.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-24 11:44:06 | ||
图片预览






文档简介
(共27张PPT)
2.1.3 空间中直线与平面之间的位置关系
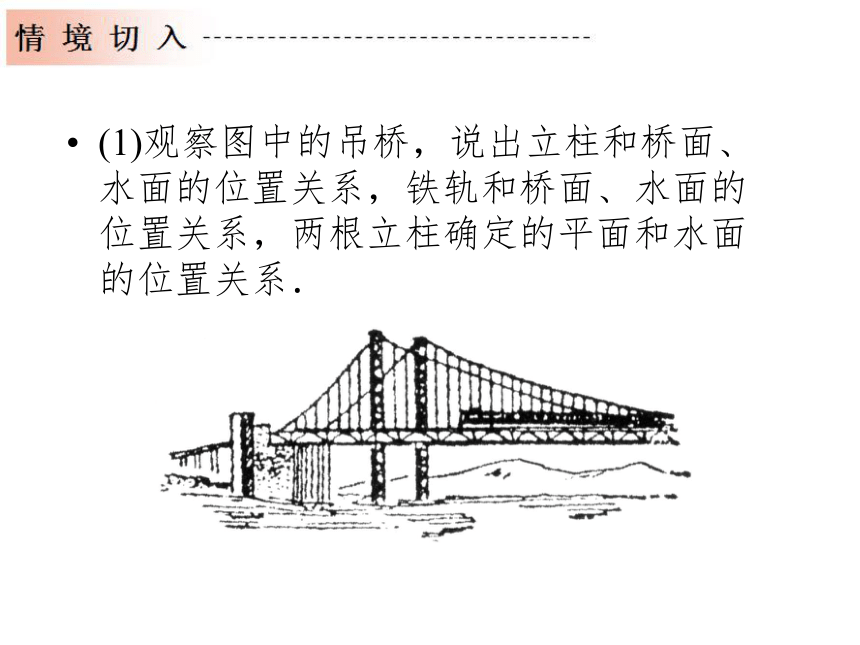
(1)观察图中的吊桥,说出立柱和桥面、水面的位置关系,铁轨和桥面、水面的位置关系,两根立柱确定的平面和水面的位置关系.
A1
B1
C1
D1
A
B
C
D
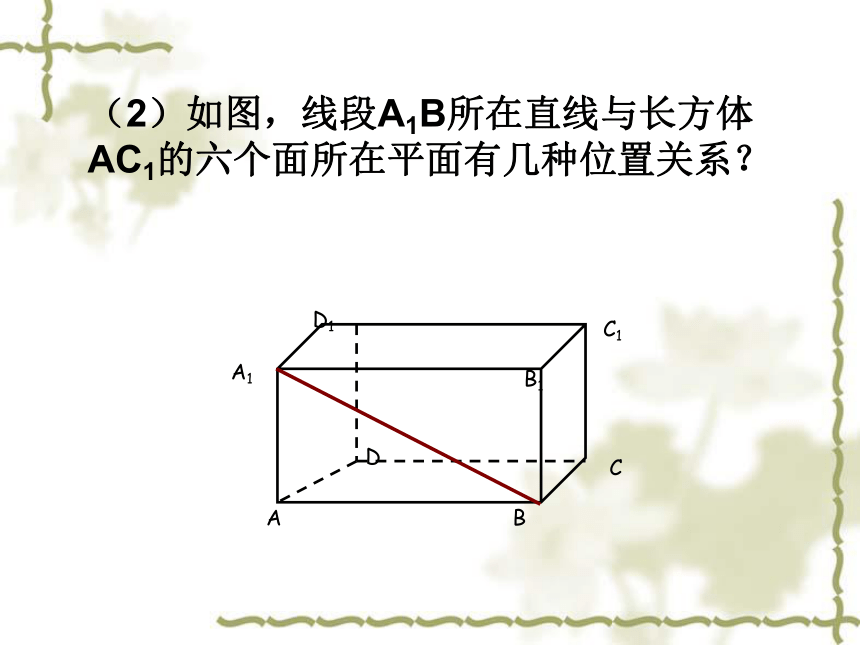
(2)如图,线段A1B所在直线与长方体AC1的六个面所在平面有几种位置关系?
(1)直线在平面内-----有无数个公共点
(2)直线在平面外:
①直线a和面α相交 :
②直线a和面α平行 :
.
A
a
a
a
a
a
a
直线与平面的位置关系有且只有三种:
(1)直线在平面内
(2)直线与平面相交
(3)直线与平面平行
直线在平面外
直线和平面相交或平行的情况统称为直线在平面外。
判断直线与平面的位置关系关键在于—判断直线与平面的交点个数。
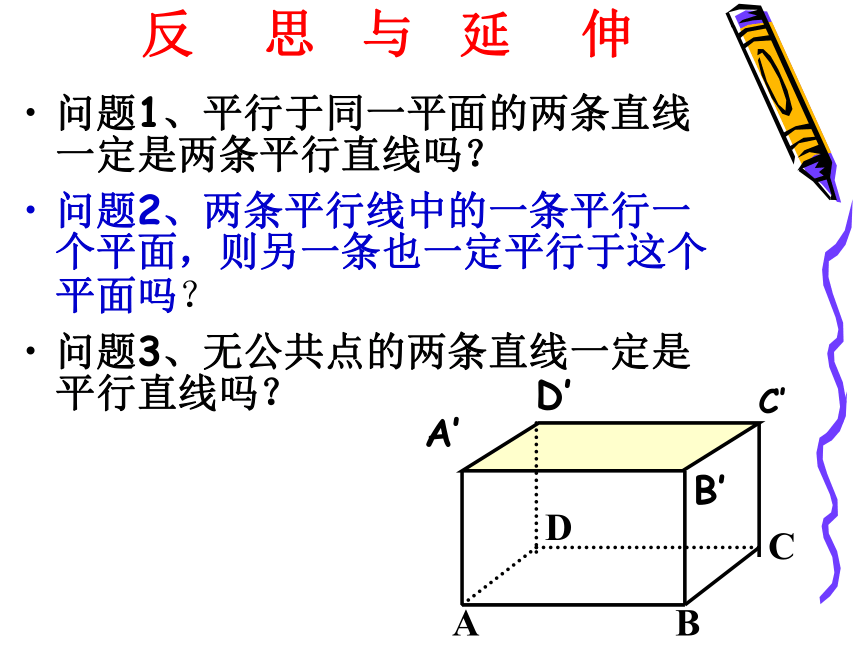
反 思 与 延 伸
问题1、平行于同一平面的两条直线一定是两条平行直线吗?
问题2、两条平行线中的一条平行一个平面,则另一条也一定平行于这个平面吗?
问题3、无公共点的两条直线一定是平行直线吗?
A
B
C
D
A′
B′
C′
D′
例4、判断下列命题的正确
(1)若直线 上有无数个点不在平面 内, 则 // 。( )
(2)若直线l与平面 平行,则l与平面 内的任意一条直线都平行。( )
(3)如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行。( )
(4)若直线l与平面 平行,则l与平面 内的
任意一条直线都没有公共点。( )
X
∨
X
X
练习、若直线a不平行平面 ,且
则下列结论成立的是( )
(A) 内所有直线与a异面
(B) 内不存在与a平行的直线
(C) 内存在唯一的直线与a平行
(D) 内的直线与a都相交
B
课本P49
巩固练习:
1.选择题
(1)以下命题(其中a,b表示直线,a表示平面)
①若a∥b,b a,则a∥a ②若a∥a,b∥a,则a∥b ③若a∥b,b∥a,则a∥a ④若a∥a,b a,则a∥b 其中正确命题的个数是 ( )
(A)0个 (B)1个 (C)2个 (D)3个
A
2.已知a∥a,b∥a,则直线a,b的位置关系
①平行;②垂直不相交;③垂直相交;
④相交;⑤不垂直且不相交.
其中可能成立的有 ( )
(A)2个 (B)3个 (C)4个 (D)5个
3.如果平面a外有两点A、B,它们到平面a的距离都是a,则直线AB和平面a的位置关系一定是( )
(A)平行 (B)相交
(C)平行或相交 (D)AB a
巩固练习:
D
C
巩固练习:
4.已知m,n为异面直线,m∥平面a,n∥平面b,a∩b=l,则l ( )
(A)与m,n都相交
(B)与m,n中至少一条相交
(C)与m,n都不相交
(D)与m,n中一条相交
C
(1)拿出两本书,看作两个平面,上下、左右移动和翻转,它们之间的位置关系有几种变化?
思考
(2)如图,围成长方体ABCD-A′B′C′D′的六个面,两两之间的位置关系有几种?
两个平面之间的位置关系有且只有以下两种
l
两个平面的位置关系
两平面平行
没有公共点
有一条公共直线
两平面相交
α∥β
α∩β=a
位置关系
公共点
符号表示
图形表示
探究:
平行或异面
课本P50
练习:
如果三个平面两两相交,那么它们的交线有多少条?画出图形表示你的结论。
一条或三条
课本P50
(1)
(2)
图形 文字语言(读法) 符号语言
A
a
A
a
点在直线上
点在直线外
点在平面内
点在平面外
(1)空间中点与线、点与面的位置关系
小结
图形 文字语言(读法) 符号语言
a∥b
(2)空间中线与线的位置关系
两直线不共面且无公共点两直线异面
两直线共面且有一个公共点两直线相交
两直线共面且无公共点两直线平行
a、b异面
aIb=A
b
a
A
b
a
b
a
图形 文字语言(读法) 符号语言
A
a
(3)空间中线与面的位置关系
直线上所有的点都在平面内直线在平面内
直线与平面有一个公共点直线与平面相交
直线与平面无公共点直线与平面平行
a
a
aI =A
a∥
a
图形 文字语言(读法) 符号语言
(4)空间中面与面的位置关系
两个平面有一公共直线两个平面相交
两个平面无公共点两个平面平行
α∥β
α
β
随堂练习
1.下列说法正确的是( )
A.如果一条直线与一个平面平行,那么这条直线与平面内任何一条直线平行。
C.过平面外一点有且只有一条直线与平面平行。
B.如果一条直线与一个平面相交,那么这条直线与平面内无数条直线垂直。
D.直线上有两个点到平面的距离相等,则这直线平行与这平面。
B
2.下列命题中正确的个数是( )
A.若直线m上有无数个点不在平面 内,则m与 平行。
B.如果直线n与平面α平行,则n 与平面α内任意一条直线都平行。
C.如果两条平行直线中的一条与一个平面平行,则另一条也与这个平面平行。
D.如果直线n与平面 平行,则n 与平面 内任意一条直线都没有公共点。
D
2.1.3 空间中直线与平面之间的位置关系
(1)观察图中的吊桥,说出立柱和桥面、水面的位置关系,铁轨和桥面、水面的位置关系,两根立柱确定的平面和水面的位置关系.
A1
B1
C1
D1
A
B
C
D
(2)如图,线段A1B所在直线与长方体AC1的六个面所在平面有几种位置关系?
(1)直线在平面内-----有无数个公共点
(2)直线在平面外:
①直线a和面α相交 :
②直线a和面α平行 :
.
A
a
a
a
a
a
a
直线与平面的位置关系有且只有三种:
(1)直线在平面内
(2)直线与平面相交
(3)直线与平面平行
直线在平面外
直线和平面相交或平行的情况统称为直线在平面外。
判断直线与平面的位置关系关键在于—判断直线与平面的交点个数。
反 思 与 延 伸
问题1、平行于同一平面的两条直线一定是两条平行直线吗?
问题2、两条平行线中的一条平行一个平面,则另一条也一定平行于这个平面吗?
问题3、无公共点的两条直线一定是平行直线吗?
A
B
C
D
A′
B′
C′
D′
例4、判断下列命题的正确
(1)若直线 上有无数个点不在平面 内, 则 // 。( )
(2)若直线l与平面 平行,则l与平面 内的任意一条直线都平行。( )
(3)如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行。( )
(4)若直线l与平面 平行,则l与平面 内的
任意一条直线都没有公共点。( )
X
∨
X
X
练习、若直线a不平行平面 ,且
则下列结论成立的是( )
(A) 内所有直线与a异面
(B) 内不存在与a平行的直线
(C) 内存在唯一的直线与a平行
(D) 内的直线与a都相交
B
课本P49
巩固练习:
1.选择题
(1)以下命题(其中a,b表示直线,a表示平面)
①若a∥b,b a,则a∥a ②若a∥a,b∥a,则a∥b ③若a∥b,b∥a,则a∥a ④若a∥a,b a,则a∥b 其中正确命题的个数是 ( )
(A)0个 (B)1个 (C)2个 (D)3个
A
2.已知a∥a,b∥a,则直线a,b的位置关系
①平行;②垂直不相交;③垂直相交;
④相交;⑤不垂直且不相交.
其中可能成立的有 ( )
(A)2个 (B)3个 (C)4个 (D)5个
3.如果平面a外有两点A、B,它们到平面a的距离都是a,则直线AB和平面a的位置关系一定是( )
(A)平行 (B)相交
(C)平行或相交 (D)AB a
巩固练习:
D
C
巩固练习:
4.已知m,n为异面直线,m∥平面a,n∥平面b,a∩b=l,则l ( )
(A)与m,n都相交
(B)与m,n中至少一条相交
(C)与m,n都不相交
(D)与m,n中一条相交
C
(1)拿出两本书,看作两个平面,上下、左右移动和翻转,它们之间的位置关系有几种变化?
思考
(2)如图,围成长方体ABCD-A′B′C′D′的六个面,两两之间的位置关系有几种?
两个平面之间的位置关系有且只有以下两种
l
两个平面的位置关系
两平面平行
没有公共点
有一条公共直线
两平面相交
α∥β
α∩β=a
位置关系
公共点
符号表示
图形表示
探究:
平行或异面
课本P50
练习:
如果三个平面两两相交,那么它们的交线有多少条?画出图形表示你的结论。
一条或三条
课本P50
(1)
(2)
图形 文字语言(读法) 符号语言
A
a
A
a
点在直线上
点在直线外
点在平面内
点在平面外
(1)空间中点与线、点与面的位置关系
小结
图形 文字语言(读法) 符号语言
a∥b
(2)空间中线与线的位置关系
两直线不共面且无公共点两直线异面
两直线共面且有一个公共点两直线相交
两直线共面且无公共点两直线平行
a、b异面
aIb=A
b
a
A
b
a
b
a
图形 文字语言(读法) 符号语言
A
a
(3)空间中线与面的位置关系
直线上所有的点都在平面内直线在平面内
直线与平面有一个公共点直线与平面相交
直线与平面无公共点直线与平面平行
a
a
aI =A
a∥
a
图形 文字语言(读法) 符号语言
(4)空间中面与面的位置关系
两个平面有一公共直线两个平面相交
两个平面无公共点两个平面平行
α∥β
α
β
随堂练习
1.下列说法正确的是( )
A.如果一条直线与一个平面平行,那么这条直线与平面内任何一条直线平行。
C.过平面外一点有且只有一条直线与平面平行。
B.如果一条直线与一个平面相交,那么这条直线与平面内无数条直线垂直。
D.直线上有两个点到平面的距离相等,则这直线平行与这平面。
B
2.下列命题中正确的个数是( )
A.若直线m上有无数个点不在平面 内,则m与 平行。
B.如果直线n与平面α平行,则n 与平面α内任意一条直线都平行。
C.如果两条平行直线中的一条与一个平面平行,则另一条也与这个平面平行。
D.如果直线n与平面 平行,则n 与平面 内任意一条直线都没有公共点。
D
