立体几何-2020-2021高考数学真题分类练习(Word版含解析)
文档属性
| 名称 | 立体几何-2020-2021高考数学真题分类练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 10:56:51 | ||
图片预览



文档简介
2020-2021真题精编-立体几何
一、空间几何体的体积、面积
1.(2021·全国·高考真题)若圆锥的轴截面为等腰直角三角形,则它的底面积与侧面积之比是( )
A. B. C. D.
2.(2021·全国·高考真题)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为( )
A. B. C. D.
3.(2021·全国·高考真题)正四棱台的上 下底面的边长分别为2,4,侧棱长为2,则其体积为( )
A. B. C. D.
4.(2021·全国·高考真题)在正三棱柱中,,点满足,其中,,则( )
A.当时,的周长为定值
B.当时,三棱锥的体积为定值
C.当时,有且仅有一个点,使得
D.当时,有且仅有一个点,使得平面
5.(2020·海南·高考真题)已知正方体ABCD-A1B1C1D1的棱长为2,M、N分别为BB1、AB的中点,则三棱锥A-NMD1的体积为____________
6.(2021·全国·高考真题(文))如图,四棱锥的底面是矩形,底面,M为的中点,且.
(1)证明:平面平面;
(2)若,求四棱锥的体积.
二、平行、垂直的命题判定
7.(2021·全国·高考真题)已知,表示平面,,表示直线,以下命题中正确的选项是( )
A.假设,,那么
B.假设,,,那么
C.假设,,那么
D.假设,,,,那么
8.(2021·全国·高考真题)设m,n为两条不同的直线,,为两个不同的平面,则下列结论正确的是( )
A.若,,则
B.若,,,则
C.若,,,则
D.若,,,则
9.(2020·山东·高考真题)已知正方体(如图所示),则下列结论正确的是( )
A. B. C. D.
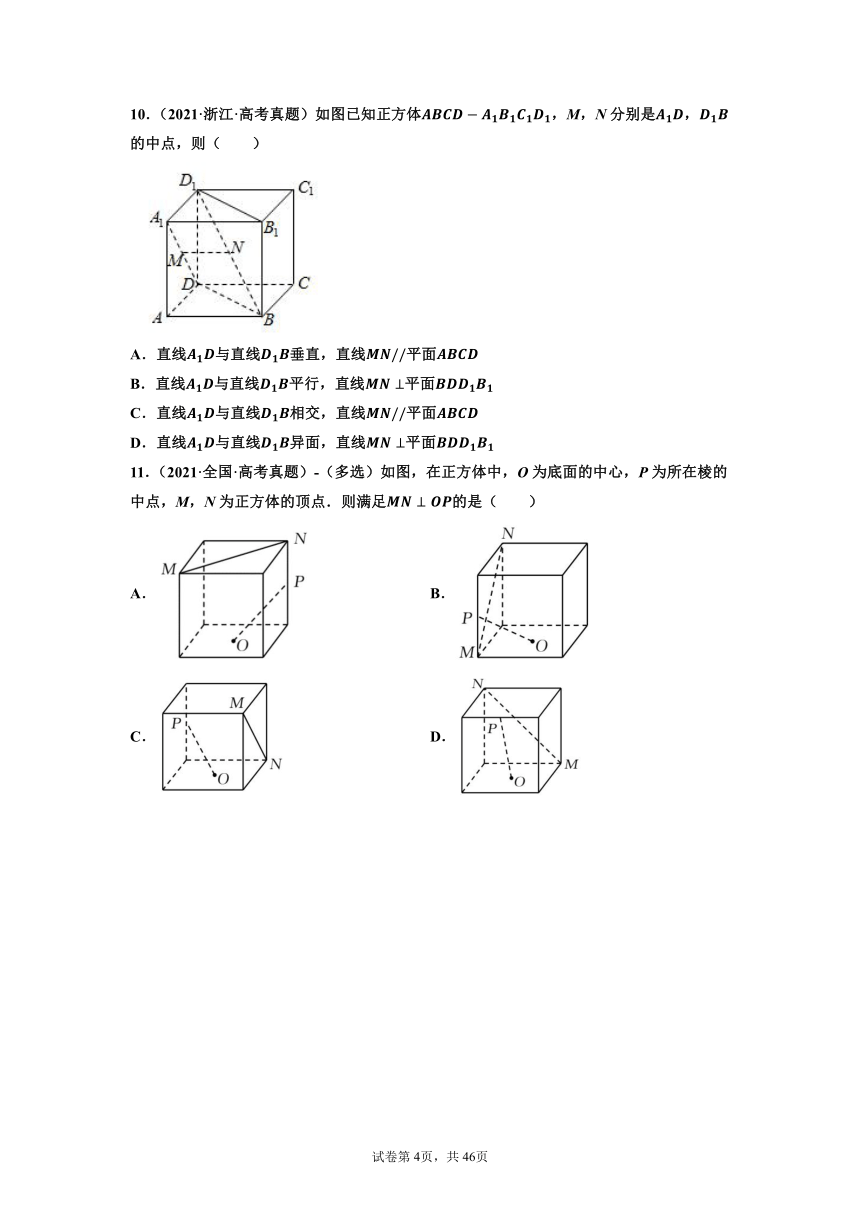
10.(2021·浙江·高考真题)如图已知正方体,M,N分别是,的中点,则( )
A.直线与直线垂直,直线平面
B.直线与直线平行,直线平面
C.直线与直线相交,直线平面
D.直线与直线异面,直线平面
11.(2021·全国·高考真题)-(多选)如图,在正方体中,O为底面的中心,P为所在棱的中点,M,N为正方体的顶点.则满足的是( )
A. B.
C. D.
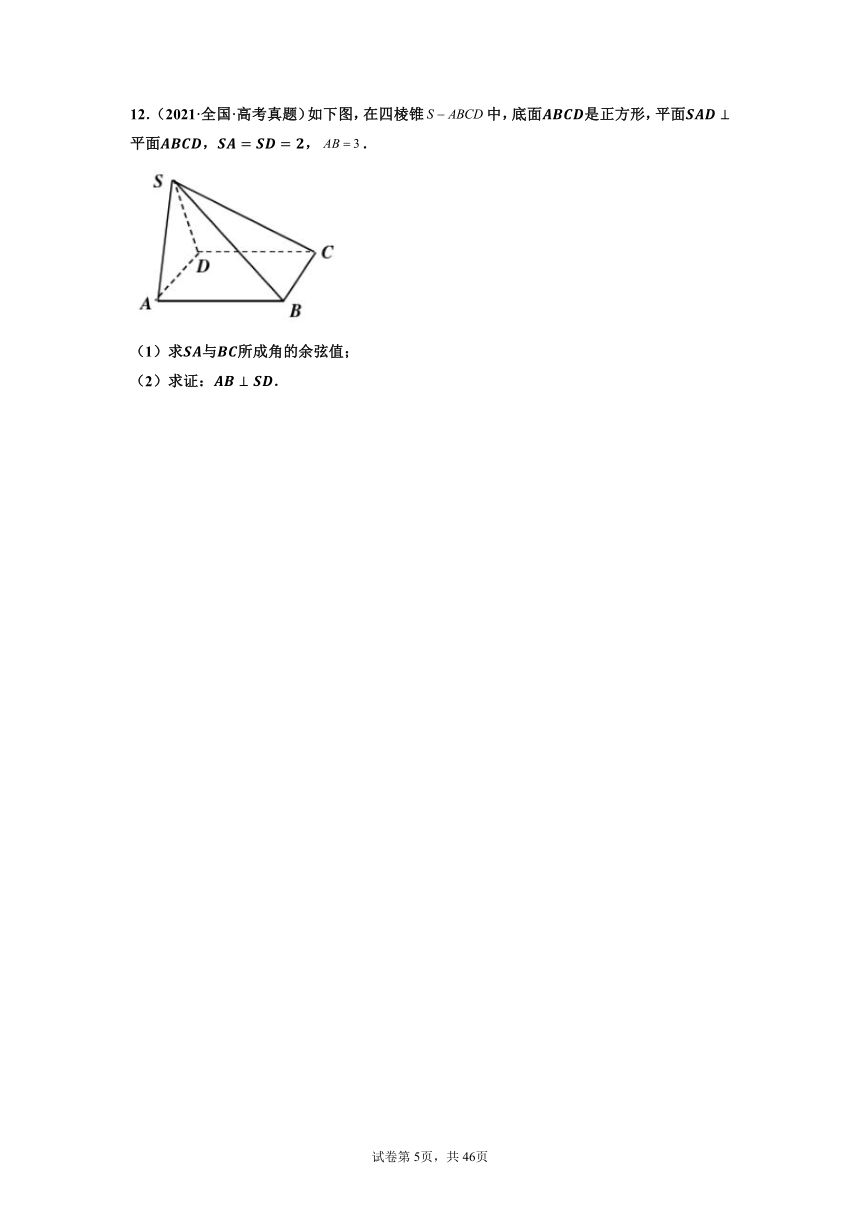
12.(2021·全国·高考真题)如下图,在四棱锥中,底面是正方形,平面平面,,.
(1)求与所成角的余弦值;
(2)求证:.
三、球体-能力拓展
13.(2020·天津·高考真题)若棱长为的正方体的顶点都在同一球面上,则该球的表面积为( )
A. B. C. D.
14.(2021·天津·高考真题)两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为,两个圆锥的高之比为,则这两个圆锥的体积之和为( )
A. B. C. D.
15.(2020·全国·高考真题(理))已知△ABC是面积为的等边三角形,且其顶点都在球O的球面上.若球O的表面积为16π,则O到平面ABC的距离为( )
A. B. C.1 D.
16.(2021·全国·高考真题(理))已如A,B,C是半径为1的球O的球面上的三个点,且,则三棱锥的体积为( )
A. B. C. D.
17.(2020·全国·高考真题(理))已知为球的球面上的三个点,⊙为的外接圆,若⊙的面积为,,则球的表面积为( )
A. B. C. D.
18.(2020·海南·高考真题)已知直四棱柱ABCD–A1B1C1D1的棱长均为2,∠BAD=60°.以为球心,为半径的球面与侧面BCC1B1的交线长为________.
四、立体几何的数学应用
19.(2021·全国·高考真题)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为(轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O,半径r为的球,其上点A的纬度是指与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为,记卫星信号覆盖地球表面的表面积为(单位:),则S占地球表面积的百分比约为( )
A.26% B.34% C.42% D.50%
20.(2021·北京·高考真题)某一时间段内,从天空降落到地面上的雨水,未经蒸发、渗漏、流失而在水平面上积聚的深度,称为这个时段的降雨量(单位:).24h降雨量的等级划分如下:
在综合实践活动中,某小组自制了一个底面直径为200 mm,高为300 mm的圆锥形雨量器.若一次降雨过程中,该雨量器收集的24h的雨水高度是150 mm(如图所示),则这24h降雨量的等级是
A.小雨 B.中雨 C.大雨 D.暴雨
21.(2020·海南·高考真题)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )
A.20° B.40°
C.50° D.90°
22.(2020·全国·高考真题(理))埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
A. B. C. D.
23.(2020·江苏·高考真题)如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm,高为2 cm,内孔半径为0.5 cm,则此六角螺帽毛坯的体积是____cm.
五、立体几何与空间向量的综合应用
24.(2021·全国·高考真题(理))在正方体中,P为的中点,则直线与所成的角为( )
A. B. C. D.
25.(2021·全国·高考真题)如图,四棱锥中,底面ABCD是矩形,平面ABCD,E为PD的中点.
(1)证明:平面ACE;
(2)设,,直线PB与平面ABCD所成的角为,求四棱锥的体积.
26.(2021·全国·高考真题)在四棱锥中,底面是正方形,若.
(1)证明:平面平面;
(2)求二面角的平面角的余弦值.
27.(2021·天津·高考真题)如图,在棱长为2的正方体中,E为棱BC的中点,F为棱CD的中点.
(I)求证:平面;
(II)求直线与平面所成角的正弦值.
(III)求二面角的正弦值.
28.(2021·全国·高考真题(理))已知直三棱柱中,侧面为正方形,,E,F分别为和的中点,D为棱上的点.
(1)证明:;
(2)当为何值时,面与面所成的二面角的正弦值最小
29.(2021·北京·高考真题)如图:在正方体中,为中点,与平面交于点.
(1)求证:为的中点;
(2)点是棱上一点,且二面角的余弦值为,求的值.
30.(2020·全国·高考真题(理))如图,为圆锥的顶点,是圆锥底面的圆心,为底面直径,.是底面的内接正三角形,为上一点,.
(1)证明:平面;
(2)求二面角的余弦值.
2020-2021真题精编-立体几何
解析版
一、空间几何体的体积、面积
1.(2021·全国·高考真题)若圆锥的轴截面为等腰直角三角形,则它的底面积与侧面积之比是( )
A. B. C. D.
【答案】C
【分析】
根据题意作图,由轴截面得出母线与底面圆半径的等量关系,再套公式求解.
【详解】
根据题意作图,
设圆锥的底面圆半径为,高为 ,母线长为 .
若圆锥的轴截面为等腰直角三角形,
则有,.
该圆锥的底面积与侧面积比值为.
故选:C.
2.(2021·全国·高考真题)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为( )
A. B. C. D.
【答案】B
【分析】
设圆锥的母线长为,根据圆锥底面圆的周长等于扇形的弧长可求得的值,即为所求.
【详解】
设圆锥的母线长为,由于圆锥底面圆的周长等于扇形的弧长,则,解得.
故选:B.
3.(2021·全国·高考真题)正四棱台的上 下底面的边长分别为2,4,侧棱长为2,则其体积为( )
A. B. C. D.
【答案】D
【分析】
由四棱台的几何特征算出该几何体的高及上下底面面积,再由棱台的体积公式即可得解.
【详解】
作出图形,连接该正四棱台上下底面的中心,如图,
因为该四棱台上下底面边长分别为2,4,侧棱长为2,
所以该棱台的高,
下底面面积,上底面面积,
所以该棱台的体积.
故选:D.
4.(2021·全国·高考真题)在正三棱柱中,,点满足,其中,,则( )
A.当时,的周长为定值
B.当时,三棱锥的体积为定值
C.当时,有且仅有一个点,使得
D.当时,有且仅有一个点,使得平面
【答案】BD
【分析】
对于A,由于等价向量关系,联系到一个三角形内,进而确定点的坐标;
对于B,将点的运动轨迹考虑到一个三角形内,确定路线,进而考虑体积是否为定值;
对于C,考虑借助向量的平移将点轨迹确定,进而考虑建立合适的直角坐标系来求解点的个数;
对于D,考虑借助向量的平移将点轨迹确定,进而考虑建立合适的直角坐标系来求解点的个数.
【详解】
易知,点在矩形内部(含边界).
对于A,当时,,即此时线段,周长不是定值,故A错误;
对于B,当时,,故此时点轨迹为线段,而,平面,则有到平面的距离为定值,所以其体积为定值,故B正确.
对于C,当时,,取,中点分别为,,则,所以点轨迹为线段,不妨建系解决,建立空间直角坐标系如图,,,,则,,,所以或.故均满足,故C错误;
对于D,当时,,取,中点为.,所以点轨迹为线段.设,因为,所以,,所以,此时与重合,故D正确.
故选:BD.
【点睛】
本题主要考查向量的等价替换,关键之处在于所求点的坐标放在三角形内.
5.(2020·海南·高考真题)已知正方体ABCD-A1B1C1D1的棱长为2,M、N分别为BB1、AB的中点,则三棱锥A-NMD1的体积为____________
【答案】
【分析】
利用计算即可.
【详解】
因为正方体ABCD-A1B1C1D1的棱长为2,M、N分别为BB1、AB的中点
所以
故答案为:
【点睛】
在求解三棱锥的体积时,要注意观察图形的特点,看把哪个当成顶点好计算一些.
6.(2021·全国·高考真题(文))如图,四棱锥的底面是矩形,底面,M为的中点,且.
(1)证明:平面平面;
(2)若,求四棱锥的体积.
【答案】(1)证明见解析;(2).
【分析】
(1)由底面可得,又,由线面垂直的判定定理可得平面,再根据面面垂直的判定定理即可证出平面平面;
(2)由(1)可知,,由平面知识可知,,由相似比可求出,再根据四棱锥的体积公式即可求出.
【详解】
(1)因为底面,平面,
所以,
又,,
所以平面,
而平面,
所以平面平面.
(2)由(1)可知,平面,所以,
从而,设,,
则,即,解得,所以.
因为底面,
故四棱锥的体积为.
【点睛】
本题第一问解题关键是找到平面或平面的垂线,结合题目条件,所以垂线可以从中产生,稍加分析即可判断出平面,从而证出;第二问关键是底面矩形面积的计算,利用第一问的结论结合平面几何知识可得出,从而求出矩形的另一个边长,从而求得该四棱锥的体积.
二、平行、垂直的命题判定
7.(2021·全国·高考真题)已知,表示平面,,表示直线,以下命题中正确的选项是( )
A.假设,,那么
B.假设,,,那么
C.假设,,那么
D.假设,,,,那么
【答案】C
【分析】
根据线面垂直的性质定理,可判断A;根据面面平行的性质定理,可判断B、C;根据面面平行的判定定理,可判定D
【详解】
选项A:假设,,那么或在内,故选项A错误;
选项B:假设,,,那么或与异面,故选项B错误;
选项D:假设,,,,且、相交才能判定,故选项C错误;
选项C:依照两平面平行的性质可知C正确.
故选:C
8.(2021·全国·高考真题)设m,n为两条不同的直线,,为两个不同的平面,则下列结论正确的是( )
A.若,,则
B.若,,,则
C.若,,,则
D.若,,,则
【答案】D
【分析】
根据线面的位置关系可判断A;举反例判断B、C;由面面垂直的判定定理可判断D,进而可得正确选项.
【详解】
对于A:若,,则或,故选项A不正确;
对于B:如图平面为平面,平面为平面,直线为,直线为,满足,,,但与相交,故选项B不正确;
对于C:如图在正方体中,平面为平面,平面为平面,直线为,直线为,满足,,,则,故选项C不正确;
对于D:若,,可得或,若,因为,由面面垂直的判定定理可得;若,可过作平面与相交,则交线在平面内,且交线与平行,由可得交线与垂直,由面面垂直的判定定理可得,故选项D正确;
故选:D.
9.(2020·山东·高考真题)已知正方体(如图所示),则下列结论正确的是( )
A. B. C. D.
【答案】D
【分析】
根据异面直线的定义,垂直关系的转化,判断选项.
【详解】
A.,与相交,所以与异面,故A错误;
B.与平面相交,且,所以与异面,故B错误;
C.四边形是矩形,不是菱形,所以对角线与不垂直,故C错误;
D.连结,,,,所以平面,所以,故D正确.
故选:D
10.(2021·浙江·高考真题)如图已知正方体,M,N分别是,的中点,则( )
A.直线与直线垂直,直线平面
B.直线与直线平行,直线平面
C.直线与直线相交,直线平面
D.直线与直线异面,直线平面
【答案】A
【分析】
由正方体间的垂直、平行关系,可证平面,即可得出结论.
【详解】
连,在正方体中,
M是的中点,所以为中点,
又N是的中点,所以,
平面平面,
所以平面.
因为不垂直,所以不垂直
则不垂直平面,所以选项B,D不正确;
在正方体中,,
平面,所以,
,所以平面,
平面,所以,
且直线是异面直线,
所以选项C错误,选项A正确.
故选:A.
【点睛】
关键点点睛:熟练掌握正方体中的垂直、平行关系是解题的关键,如两条棱平行或垂直,同一个面对角线互相垂直,正方体的对角线与面的对角线是相交但不垂直或异面垂直关系.
11.(2021·全国·高考真题)如图,在正方体中,O为底面的中心,P为所在棱的中点,M,N为正方体的顶点.则满足的是( )
A. B.
C. D.
【答案】BC
【分析】
根据线面垂直的判定定理可得BC的正误,平移直线构造所考虑的线线角后可判断AD的正误.
【详解】
设正方体的棱长为,
对于A,如图(1)所示,连接,则,
故(或其补角)为异面直线所成的角,
在直角三角形,,,故,
故不成立,故A错误.
对于B,如图(2)所示,取的中点为,连接,,则,,
由正方体可得平面,而平面,
故,而,故平面,
又平面,,而,
所以平面,而平面,故,故B正确.
对于C,如图(3),连接,则,由B的判断可得,
故,故C正确.
对于D,如图(4),取的中点,的中点,连接,
则,
因为,故,故,
所以或其补角为异面直线所成的角,
因为正方体的棱长为2,故,,
,,故不是直角,
故不垂直,故D错误.
故选:BC.
12.(2021·全国·高考真题)如下图,在四棱锥中,底面是正方形,平面平面,,.
(1)求与所成角的余弦值;
(2)求证:.
【答案】(1);(2)证明见解析.
【分析】
(1)由题意可得 即为SA 与 BC所成的角,根据余弦定理计算即可;
(2)结合面面垂直的性质和线面垂直的性质即可证明.
【详解】
【考查内容】异面直线所成的角,直线与平面垂直的判定和性质
【解】(1)因为,因此即为与所成的角,在中,,
又在正方形中,因此,
因此与所成角的余弦值是.
(2)因为平面平面,平面平面,在正方形中,,
因此平面,又因为平面,因此.
三、球体-能力拓展
13.(2020·天津·高考真题)若棱长为的正方体的顶点都在同一球面上,则该球的表面积为( )
A. B. C. D.
【答案】C
【分析】
求出正方体的体对角线的一半,即为球的半径,利用球的表面积公式,即可得解.
【详解】
这个球是正方体的外接球,其半径等于正方体的体对角线的一半,
即,
所以,这个球的表面积为.
故选:C.
【点睛】
本题考查正方体的外接球的表面积的求法,求出外接球的半径是本题的解题关键,属于基础题.求多面体的外接球的面积和体积问题,常用方法有:(1)三条棱两两互相垂直时,可恢复为长方体,利用长方体的体对角线为外接球的直径,求出球的半径;(2)直棱柱的外接球可利用棱柱的上下底面平行,借助球的对称性,球心为上下底面外接圆的圆心连线的中点,再根据勾股定理求球的半径;(3)如果设计几何体有两个面相交,可过两个面的外心分别作两个面的垂线,垂线的交点为几何体的球心.
14.(2021·天津·高考真题)两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为,两个圆锥的高之比为,则这两个圆锥的体积之和为( )
A. B. C. D.
【答案】B
【分析】
作出图形,计算球体的半径,可计算得出两圆锥的高,利用三角形相似计算出圆锥的底面圆半径,再利用锥体体积公式可求得结果.
【详解】
如下图所示,设两个圆锥的底面圆圆心为点,
设圆锥和圆锥的高之比为,即,
设球的半径为,则,可得,所以,,
所以,,,
,则,所以,,
又因为,所以,,
所以,,,
因此,这两个圆锥的体积之和为.
故选:B.
15.(2020·全国·高考真题(理))已知△ABC是面积为的等边三角形,且其顶点都在球O的球面上.若球O的表面积为16π,则O到平面ABC的距离为( )
A. B. C.1 D.
【答案】C
【分析】
根据球的表面积和的面积可求得球的半径和外接圆半径,由球的性质可知所求距离.
【详解】
设球的半径为,则,解得:.
设外接圆半径为,边长为,
是面积为的等边三角形,
,解得:,,
球心到平面的距离.
故选:C.
【点睛】
本题考查球的相关问题的求解,涉及到球的表面积公式和三角形面积公式的应用;解题关键是明确球的性质,即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.
16.(2021·全国·高考真题(理))已如A,B,C是半径为1的球O的球面上的三个点,且,则三棱锥的体积为( )
A. B. C. D.
【答案】A
【分析】
由题可得为等腰直角三角形,得出外接圆的半径,则可求得到平面的距离,进而求得体积.
【详解】
,为等腰直角三角形,,
则外接圆的半径为,又球的半径为1,
设到平面的距离为,
则,
所以.
故选:A.
【点睛】
关键点睛:本题考查球内几何体问题,解题的关键是正确利用截面圆半径、球半径、球心到截面距离的勾股关系求解.
17.(2020·全国·高考真题(理))已知为球的球面上的三个点,⊙为的外接圆,若⊙的面积为,,则球的表面积为( )
A. B. C. D.
【答案】A
【分析】
由已知可得等边的外接圆半径,进而求出其边长,得出的值,根据球的截面性质,求出球的半径,即可得出结论.
【详解】
设圆半径为,球的半径为,依题意,
得,为等边三角形,
由正弦定理可得,
,根据球的截面性质平面,
,
球的表面积.
故选:A
【点睛】
本题考查球的表面积,应用球的截面性质是解题的关键,考查计算求解能力,属于基础题.
18.(2020·海南·高考真题)已知直四棱柱ABCD–A1B1C1D1的棱长均为2,∠BAD=60°.以为球心,为半径的球面与侧面BCC1B1的交线长为________.
【答案】.
【分析】
根据已知条件易得,侧面,可得侧面与球面的交线上的点到的距离为,可得侧面与球面的交线是扇形的弧,再根据弧长公式可求得结果.
【详解】
如图:
取的中点为,的中点为,的中点为,
因为60°,直四棱柱的棱长均为2,所以△为等边三角形,所以,,
又四棱柱为直四棱柱,所以平面,所以,
因为,所以侧面,
设为侧面与球面的交线上的点,则,
因为球的半径为,,所以,
所以侧面与球面的交线上的点到的距离为,
因为,所以侧面与球面的交线是扇形的弧,
因为,所以,
所以根据弧长公式可得.
故答案为:.
【点睛】
本题考查了直棱柱的结构特征,考查了直线与平面垂直的判定,考查了立体几何中的轨迹问题,考查了扇形中的弧长公式,属于中档题.
四、立体几何的数学应用
19.(2021·全国·高考真题)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为(轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O,半径r为的球,其上点A的纬度是指与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为,记卫星信号覆盖地球表面的表面积为(单位:),则S占地球表面积的百分比约为( )
A.26% B.34% C.42% D.50%
【答案】C
【分析】
由题意结合所给的表面积公式和球的表面积公式整理计算即可求得最终结果.
【详解】
由题意可得,S占地球表面积的百分比约为:
.
故选:C.
20.(2021·北京·高考真题)某一时间段内,从天空降落到地面上的雨水,未经蒸发、渗漏、流失而在水平面上积聚的深度,称为这个时段的降雨量(单位:).24h降雨量的等级划分如下:
在综合实践活动中,某小组自制了一个底面直径为200 mm,高为300 mm的圆锥形雨量器.若一次降雨过程中,该雨量器收集的24h的雨水高度是150 mm(如图所示),则这24h降雨量的等级是
A.小雨 B.中雨 C.大雨 D.暴雨
【答案】B
【分析】
计算出圆锥体积,除以圆面的面积即可得降雨量,即可得解.
【详解】
由题意,一个半径为的圆面内的降雨充满一个底面半径为,高为的圆锥,
所以积水厚度,属于中雨.
故选:B.
21.(2020·海南·高考真题)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )
A.20° B.40°
C.50° D.90°
【答案】B
【分析】
画出过球心和晷针所确定的平面截地球和晷面的截面图,根据面面平行的性质定理和线面垂直的定义判定有关截线的关系,根据点处的纬度,计算出晷针与点处的水平面所成角.
【详解】
画出截面图如下图所示,其中是赤道所在平面的截线;是点处的水平面的截线,依题意可知;是晷针所在直线.是晷面的截线,依题意依题意,晷面和赤道平面平行,晷针与晷面垂直,
根据平面平行的性质定理可得可知、根据线面垂直的定义可得..
由于,所以,
由于,
所以,也即晷针与点处的水平面所成角为.
故选:B
【点睛】
本小题主要考查中国古代数学文化,考查球体有关计算,涉及平面平行,线面垂直的性质,属于中档题.
22.(2020·全国·高考真题(理))埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
A. B. C. D.
【答案】C
【分析】
设,利用得到关于的方程,解方程即可得到答案.
【详解】
如图,设,则,
由题意,即,化简得,
解得(负值舍去).
故选:C.
【点晴】
本题主要考查正四棱锥的概念及其有关计算,考查学生的数学计算能力,是一道容易题.
23.(2020·江苏·高考真题)如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm,高为2 cm,内孔半径为0.5 cm,则此六角螺帽毛坯的体积是____cm.
【答案】
【分析】
先求正六棱柱体积,再求圆柱体积,相减得结果.
【详解】
正六棱柱体积为
圆柱体积为
所求几何体体积为
故答案为:
【点睛】
本题考查正六棱柱体积、圆柱体积,考查基本分析求解能力,属基础题.
五、立体几何与空间向量的综合应用
24.(2021·全国·高考真题(理))在正方体中,P为的中点,则直线与所成的角为( )
A. B. C. D.
【答案】D
【分析】
平移直线至,将直线与所成的角转化为与所成的角,解三角形即可.
【详解】
如图,连接,因为∥,
所以或其补角为直线与所成的角,
因为平面,所以,又,,
所以平面,所以,
设正方体棱长为2,则,
,所以.
故选:D
25.(2021·湖南·高考真题)如图,四棱锥中,底面ABCD是矩形,平面ABCD,E为PD的中点.
(1)证明:平面ACE;
(2)设,,直线PB与平面ABCD所成的角为,求四棱锥的体积.
【答案】(1)证明见解析;(2).
【分析】
(1) 连接交于点,连接,由三角形的中位线定理可知,结合线面平行的判定定理可证明平面.
(2)由题意可知,再运用锥体体积公式可求得四棱锥的体积.
【详解】
(1)连接交于点,连接. 在中,因为,
所以,因为平面,平面,则平面.
(2)因为平面ABCD,所以就是直线PB与平面ABCD所成的角,所以,
又,,所以,
所以四棱锥的体积,
所以四棱锥的体积为.
26.(2021·全国·高考真题)在四棱锥中,底面是正方形,若.
(1)证明:平面平面;
(2)求二面角的平面角的余弦值.
【答案】(1)证明见解析;(2).
【分析】
(1)取的中点为,连接,可证平面,从而得到面面.
(2)在平面内,过作,交于,则,建如图所示的空间坐标系,求出平面、平面的法向量后可求二面角的余弦值.
【详解】
(1)取的中点为,连接.
因为,,则,
而,故.
在正方形中,因为,故,故,
因为,故,故为直角三角形且,
因为,故平面,
因为平面,故平面平面.
(2)在平面内,过作,交于,则,
结合(1)中的平面,故可建如图所示的空间坐标系.
则,故.
设平面的法向量,
则即,取,则,
故.
而平面的法向量为,故.
二面角的平面角为锐角,故其余弦值为.
27.(2021·天津·高考真题)如图,在棱长为2的正方体中,E为棱BC的中点,F为棱CD的中点.
(I)求证:平面;
(II)求直线与平面所成角的正弦值.
(III)求二面角的正弦值.
【答案】(I)证明见解析;(II);(III).
【分析】
(I)建立空间直角坐标系,求出及平面的一个法向量,证明,即可得证;
(II)求出,由运算即可得解;
(III)求得平面的一个法向量,由结合同角三角函数的平方关系即可得解.
【详解】
(I)以为原点,分别为轴,建立如图空间直角坐标系,
则,,,,,,,
因为E为棱BC的中点,F为棱CD的中点,所以,,
所以,,,
设平面的一个法向量为,
则,令,则,
因为,所以,
因为平面,所以平面;
(II)由(1)得,,
设直线与平面所成角为,
则;
(III)由正方体的特征可得,平面的一个法向量为,
则,
所以二面角的正弦值为.
28.(2021·全国·高考真题(理))已知直三棱柱中,侧面为正方形,,E,F分别为和的中点,D为棱上的点.
(1)证明:;
(2)当为何值时,面与面所成的二面角的正弦值最小
【答案】(1)见解析;(2)
【分析】
通过已知条件,确定三条互相垂直的直线,建立合适的空间直角坐标系,借助空间向量证明线线垂直和求出二面角的平面角的余弦值最大,进而可以确定出答案.
【详解】
因为三棱柱是直三棱柱,所以底面,所以
因为,,所以,
又,所以平面.
所以两两垂直.
以为坐标原点,分别以所在直线为轴建立空间直角坐标系,如图.
所以,
.
由题设().
(1)因为,
所以,所以.
(2)设平面的法向量为,
因为,
所以,即.
令,则
因为平面的法向量为,
设平面与平面的二面角的平面角为,
则.
当时,取最小值为,
此时取最大值为.
所以,
此时.
【点睛】
本题考查空间向量的相关计算,能够根据题意设出(),在第二问中通过余弦值最大,找到正弦值最小是关键一步.
29.(2021·北京·高考真题)如图:在正方体中,为中点,与平面交于点.
(1)求证:为的中点;
(2)点是棱上一点,且二面角的余弦值为,求的值.
【答案】(1)证明见解析;(2).
【分析】
(1)首先将平面进行扩展,然后结合所得的平面与直线的交点即可证得题中的结论;
(2)建立空间直角坐标系,利用空间直角坐标系求得相应平面的法向量,然后解方程即可求得实数的值.
【详解】
(1)如图所示,取的中点,连结,
由于为正方体,为中点,故,
从而四点共面,即平面CDE即平面,
据此可得:直线交平面于点,
当直线与平面相交时只有唯一的交点,故点与点重合,
即点为中点.
(2)以点为坐标原点,方向分别为轴,轴,轴正方形,建立空间直角坐标系,
不妨设正方体的棱长为2,设,
则:,
从而:,
设平面的法向量为:,则:
,
令可得:,
设平面的法向量为:,则:
,
令可得:,
从而:,
则:,
整理可得:,故(舍去).
【点睛】
本题考查了立体几何中的线面关系和二面角的求解问题,意在考查学生的空间想象能力和逻辑推理能力,对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解.
30.(2020·全国·高考真题(理))如图,为圆锥的顶点,是圆锥底面的圆心,为底面直径,.是底面的内接正三角形,为上一点,.
(1)证明:平面;
(2)求二面角的余弦值.
【答案】(1)证明见解析;(2).
【分析】
(1)要证明平面,只需证明,即可;
(2)以O为坐标原点,OA为x轴,ON为y轴建立如图所示的空间直角坐标系,分别算出平面的法向量为,平面的法向量为,利用公式计算即可得到答案.
【详解】
(1)由题设,知为等边三角形,设,
则,,所以,
又为等边三角形,则,所以,
,则,所以,
同理,又,所以平面;
(2)过O作∥BC交AB于点N,因为平面,以O为坐标原点,OA为x轴,ON为y轴建立如图所示的空间直角坐标系,
则,
,,,
设平面的一个法向量为,
由,得,令,得,
所以,
设平面的一个法向量为
由,得,令,得,
所以
故,
设二面角的大小为,则.
【点晴】
本题主要考查线面垂直的证明以及利用向量求二面角的大小,考查学生空间想象能力,数学运算能力,是一道容易题.
试卷第2页,共31页
试卷第1页,共1页
一、空间几何体的体积、面积
1.(2021·全国·高考真题)若圆锥的轴截面为等腰直角三角形,则它的底面积与侧面积之比是( )
A. B. C. D.
2.(2021·全国·高考真题)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为( )
A. B. C. D.
3.(2021·全国·高考真题)正四棱台的上 下底面的边长分别为2,4,侧棱长为2,则其体积为( )
A. B. C. D.
4.(2021·全国·高考真题)在正三棱柱中,,点满足,其中,,则( )
A.当时,的周长为定值
B.当时,三棱锥的体积为定值
C.当时,有且仅有一个点,使得
D.当时,有且仅有一个点,使得平面
5.(2020·海南·高考真题)已知正方体ABCD-A1B1C1D1的棱长为2,M、N分别为BB1、AB的中点,则三棱锥A-NMD1的体积为____________
6.(2021·全国·高考真题(文))如图,四棱锥的底面是矩形,底面,M为的中点,且.
(1)证明:平面平面;
(2)若,求四棱锥的体积.
二、平行、垂直的命题判定
7.(2021·全国·高考真题)已知,表示平面,,表示直线,以下命题中正确的选项是( )
A.假设,,那么
B.假设,,,那么
C.假设,,那么
D.假设,,,,那么
8.(2021·全国·高考真题)设m,n为两条不同的直线,,为两个不同的平面,则下列结论正确的是( )
A.若,,则
B.若,,,则
C.若,,,则
D.若,,,则
9.(2020·山东·高考真题)已知正方体(如图所示),则下列结论正确的是( )
A. B. C. D.
10.(2021·浙江·高考真题)如图已知正方体,M,N分别是,的中点,则( )
A.直线与直线垂直,直线平面
B.直线与直线平行,直线平面
C.直线与直线相交,直线平面
D.直线与直线异面,直线平面
11.(2021·全国·高考真题)-(多选)如图,在正方体中,O为底面的中心,P为所在棱的中点,M,N为正方体的顶点.则满足的是( )
A. B.
C. D.
12.(2021·全国·高考真题)如下图,在四棱锥中,底面是正方形,平面平面,,.
(1)求与所成角的余弦值;
(2)求证:.
三、球体-能力拓展
13.(2020·天津·高考真题)若棱长为的正方体的顶点都在同一球面上,则该球的表面积为( )
A. B. C. D.
14.(2021·天津·高考真题)两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为,两个圆锥的高之比为,则这两个圆锥的体积之和为( )
A. B. C. D.
15.(2020·全国·高考真题(理))已知△ABC是面积为的等边三角形,且其顶点都在球O的球面上.若球O的表面积为16π,则O到平面ABC的距离为( )
A. B. C.1 D.
16.(2021·全国·高考真题(理))已如A,B,C是半径为1的球O的球面上的三个点,且,则三棱锥的体积为( )
A. B. C. D.
17.(2020·全国·高考真题(理))已知为球的球面上的三个点,⊙为的外接圆,若⊙的面积为,,则球的表面积为( )
A. B. C. D.
18.(2020·海南·高考真题)已知直四棱柱ABCD–A1B1C1D1的棱长均为2,∠BAD=60°.以为球心,为半径的球面与侧面BCC1B1的交线长为________.
四、立体几何的数学应用
19.(2021·全国·高考真题)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为(轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O,半径r为的球,其上点A的纬度是指与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为,记卫星信号覆盖地球表面的表面积为(单位:),则S占地球表面积的百分比约为( )
A.26% B.34% C.42% D.50%
20.(2021·北京·高考真题)某一时间段内,从天空降落到地面上的雨水,未经蒸发、渗漏、流失而在水平面上积聚的深度,称为这个时段的降雨量(单位:).24h降雨量的等级划分如下:
在综合实践活动中,某小组自制了一个底面直径为200 mm,高为300 mm的圆锥形雨量器.若一次降雨过程中,该雨量器收集的24h的雨水高度是150 mm(如图所示),则这24h降雨量的等级是
A.小雨 B.中雨 C.大雨 D.暴雨
21.(2020·海南·高考真题)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )
A.20° B.40°
C.50° D.90°
22.(2020·全国·高考真题(理))埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
A. B. C. D.
23.(2020·江苏·高考真题)如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm,高为2 cm,内孔半径为0.5 cm,则此六角螺帽毛坯的体积是____cm.
五、立体几何与空间向量的综合应用
24.(2021·全国·高考真题(理))在正方体中,P为的中点,则直线与所成的角为( )
A. B. C. D.
25.(2021·全国·高考真题)如图,四棱锥中,底面ABCD是矩形,平面ABCD,E为PD的中点.
(1)证明:平面ACE;
(2)设,,直线PB与平面ABCD所成的角为,求四棱锥的体积.
26.(2021·全国·高考真题)在四棱锥中,底面是正方形,若.
(1)证明:平面平面;
(2)求二面角的平面角的余弦值.
27.(2021·天津·高考真题)如图,在棱长为2的正方体中,E为棱BC的中点,F为棱CD的中点.
(I)求证:平面;
(II)求直线与平面所成角的正弦值.
(III)求二面角的正弦值.
28.(2021·全国·高考真题(理))已知直三棱柱中,侧面为正方形,,E,F分别为和的中点,D为棱上的点.
(1)证明:;
(2)当为何值时,面与面所成的二面角的正弦值最小
29.(2021·北京·高考真题)如图:在正方体中,为中点,与平面交于点.
(1)求证:为的中点;
(2)点是棱上一点,且二面角的余弦值为,求的值.
30.(2020·全国·高考真题(理))如图,为圆锥的顶点,是圆锥底面的圆心,为底面直径,.是底面的内接正三角形,为上一点,.
(1)证明:平面;
(2)求二面角的余弦值.
2020-2021真题精编-立体几何
解析版
一、空间几何体的体积、面积
1.(2021·全国·高考真题)若圆锥的轴截面为等腰直角三角形,则它的底面积与侧面积之比是( )
A. B. C. D.
【答案】C
【分析】
根据题意作图,由轴截面得出母线与底面圆半径的等量关系,再套公式求解.
【详解】
根据题意作图,
设圆锥的底面圆半径为,高为 ,母线长为 .
若圆锥的轴截面为等腰直角三角形,
则有,.
该圆锥的底面积与侧面积比值为.
故选:C.
2.(2021·全国·高考真题)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为( )
A. B. C. D.
【答案】B
【分析】
设圆锥的母线长为,根据圆锥底面圆的周长等于扇形的弧长可求得的值,即为所求.
【详解】
设圆锥的母线长为,由于圆锥底面圆的周长等于扇形的弧长,则,解得.
故选:B.
3.(2021·全国·高考真题)正四棱台的上 下底面的边长分别为2,4,侧棱长为2,则其体积为( )
A. B. C. D.
【答案】D
【分析】
由四棱台的几何特征算出该几何体的高及上下底面面积,再由棱台的体积公式即可得解.
【详解】
作出图形,连接该正四棱台上下底面的中心,如图,
因为该四棱台上下底面边长分别为2,4,侧棱长为2,
所以该棱台的高,
下底面面积,上底面面积,
所以该棱台的体积.
故选:D.
4.(2021·全国·高考真题)在正三棱柱中,,点满足,其中,,则( )
A.当时,的周长为定值
B.当时,三棱锥的体积为定值
C.当时,有且仅有一个点,使得
D.当时,有且仅有一个点,使得平面
【答案】BD
【分析】
对于A,由于等价向量关系,联系到一个三角形内,进而确定点的坐标;
对于B,将点的运动轨迹考虑到一个三角形内,确定路线,进而考虑体积是否为定值;
对于C,考虑借助向量的平移将点轨迹确定,进而考虑建立合适的直角坐标系来求解点的个数;
对于D,考虑借助向量的平移将点轨迹确定,进而考虑建立合适的直角坐标系来求解点的个数.
【详解】
易知,点在矩形内部(含边界).
对于A,当时,,即此时线段,周长不是定值,故A错误;
对于B,当时,,故此时点轨迹为线段,而,平面,则有到平面的距离为定值,所以其体积为定值,故B正确.
对于C,当时,,取,中点分别为,,则,所以点轨迹为线段,不妨建系解决,建立空间直角坐标系如图,,,,则,,,所以或.故均满足,故C错误;
对于D,当时,,取,中点为.,所以点轨迹为线段.设,因为,所以,,所以,此时与重合,故D正确.
故选:BD.
【点睛】
本题主要考查向量的等价替换,关键之处在于所求点的坐标放在三角形内.
5.(2020·海南·高考真题)已知正方体ABCD-A1B1C1D1的棱长为2,M、N分别为BB1、AB的中点,则三棱锥A-NMD1的体积为____________
【答案】
【分析】
利用计算即可.
【详解】
因为正方体ABCD-A1B1C1D1的棱长为2,M、N分别为BB1、AB的中点
所以
故答案为:
【点睛】
在求解三棱锥的体积时,要注意观察图形的特点,看把哪个当成顶点好计算一些.
6.(2021·全国·高考真题(文))如图,四棱锥的底面是矩形,底面,M为的中点,且.
(1)证明:平面平面;
(2)若,求四棱锥的体积.
【答案】(1)证明见解析;(2).
【分析】
(1)由底面可得,又,由线面垂直的判定定理可得平面,再根据面面垂直的判定定理即可证出平面平面;
(2)由(1)可知,,由平面知识可知,,由相似比可求出,再根据四棱锥的体积公式即可求出.
【详解】
(1)因为底面,平面,
所以,
又,,
所以平面,
而平面,
所以平面平面.
(2)由(1)可知,平面,所以,
从而,设,,
则,即,解得,所以.
因为底面,
故四棱锥的体积为.
【点睛】
本题第一问解题关键是找到平面或平面的垂线,结合题目条件,所以垂线可以从中产生,稍加分析即可判断出平面,从而证出;第二问关键是底面矩形面积的计算,利用第一问的结论结合平面几何知识可得出,从而求出矩形的另一个边长,从而求得该四棱锥的体积.
二、平行、垂直的命题判定
7.(2021·全国·高考真题)已知,表示平面,,表示直线,以下命题中正确的选项是( )
A.假设,,那么
B.假设,,,那么
C.假设,,那么
D.假设,,,,那么
【答案】C
【分析】
根据线面垂直的性质定理,可判断A;根据面面平行的性质定理,可判断B、C;根据面面平行的判定定理,可判定D
【详解】
选项A:假设,,那么或在内,故选项A错误;
选项B:假设,,,那么或与异面,故选项B错误;
选项D:假设,,,,且、相交才能判定,故选项C错误;
选项C:依照两平面平行的性质可知C正确.
故选:C
8.(2021·全国·高考真题)设m,n为两条不同的直线,,为两个不同的平面,则下列结论正确的是( )
A.若,,则
B.若,,,则
C.若,,,则
D.若,,,则
【答案】D
【分析】
根据线面的位置关系可判断A;举反例判断B、C;由面面垂直的判定定理可判断D,进而可得正确选项.
【详解】
对于A:若,,则或,故选项A不正确;
对于B:如图平面为平面,平面为平面,直线为,直线为,满足,,,但与相交,故选项B不正确;
对于C:如图在正方体中,平面为平面,平面为平面,直线为,直线为,满足,,,则,故选项C不正确;
对于D:若,,可得或,若,因为,由面面垂直的判定定理可得;若,可过作平面与相交,则交线在平面内,且交线与平行,由可得交线与垂直,由面面垂直的判定定理可得,故选项D正确;
故选:D.
9.(2020·山东·高考真题)已知正方体(如图所示),则下列结论正确的是( )
A. B. C. D.
【答案】D
【分析】
根据异面直线的定义,垂直关系的转化,判断选项.
【详解】
A.,与相交,所以与异面,故A错误;
B.与平面相交,且,所以与异面,故B错误;
C.四边形是矩形,不是菱形,所以对角线与不垂直,故C错误;
D.连结,,,,所以平面,所以,故D正确.
故选:D
10.(2021·浙江·高考真题)如图已知正方体,M,N分别是,的中点,则( )
A.直线与直线垂直,直线平面
B.直线与直线平行,直线平面
C.直线与直线相交,直线平面
D.直线与直线异面,直线平面
【答案】A
【分析】
由正方体间的垂直、平行关系,可证平面,即可得出结论.
【详解】
连,在正方体中,
M是的中点,所以为中点,
又N是的中点,所以,
平面平面,
所以平面.
因为不垂直,所以不垂直
则不垂直平面,所以选项B,D不正确;
在正方体中,,
平面,所以,
,所以平面,
平面,所以,
且直线是异面直线,
所以选项C错误,选项A正确.
故选:A.
【点睛】
关键点点睛:熟练掌握正方体中的垂直、平行关系是解题的关键,如两条棱平行或垂直,同一个面对角线互相垂直,正方体的对角线与面的对角线是相交但不垂直或异面垂直关系.
11.(2021·全国·高考真题)如图,在正方体中,O为底面的中心,P为所在棱的中点,M,N为正方体的顶点.则满足的是( )
A. B.
C. D.
【答案】BC
【分析】
根据线面垂直的判定定理可得BC的正误,平移直线构造所考虑的线线角后可判断AD的正误.
【详解】
设正方体的棱长为,
对于A,如图(1)所示,连接,则,
故(或其补角)为异面直线所成的角,
在直角三角形,,,故,
故不成立,故A错误.
对于B,如图(2)所示,取的中点为,连接,,则,,
由正方体可得平面,而平面,
故,而,故平面,
又平面,,而,
所以平面,而平面,故,故B正确.
对于C,如图(3),连接,则,由B的判断可得,
故,故C正确.
对于D,如图(4),取的中点,的中点,连接,
则,
因为,故,故,
所以或其补角为异面直线所成的角,
因为正方体的棱长为2,故,,
,,故不是直角,
故不垂直,故D错误.
故选:BC.
12.(2021·全国·高考真题)如下图,在四棱锥中,底面是正方形,平面平面,,.
(1)求与所成角的余弦值;
(2)求证:.
【答案】(1);(2)证明见解析.
【分析】
(1)由题意可得 即为SA 与 BC所成的角,根据余弦定理计算即可;
(2)结合面面垂直的性质和线面垂直的性质即可证明.
【详解】
【考查内容】异面直线所成的角,直线与平面垂直的判定和性质
【解】(1)因为,因此即为与所成的角,在中,,
又在正方形中,因此,
因此与所成角的余弦值是.
(2)因为平面平面,平面平面,在正方形中,,
因此平面,又因为平面,因此.
三、球体-能力拓展
13.(2020·天津·高考真题)若棱长为的正方体的顶点都在同一球面上,则该球的表面积为( )
A. B. C. D.
【答案】C
【分析】
求出正方体的体对角线的一半,即为球的半径,利用球的表面积公式,即可得解.
【详解】
这个球是正方体的外接球,其半径等于正方体的体对角线的一半,
即,
所以,这个球的表面积为.
故选:C.
【点睛】
本题考查正方体的外接球的表面积的求法,求出外接球的半径是本题的解题关键,属于基础题.求多面体的外接球的面积和体积问题,常用方法有:(1)三条棱两两互相垂直时,可恢复为长方体,利用长方体的体对角线为外接球的直径,求出球的半径;(2)直棱柱的外接球可利用棱柱的上下底面平行,借助球的对称性,球心为上下底面外接圆的圆心连线的中点,再根据勾股定理求球的半径;(3)如果设计几何体有两个面相交,可过两个面的外心分别作两个面的垂线,垂线的交点为几何体的球心.
14.(2021·天津·高考真题)两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为,两个圆锥的高之比为,则这两个圆锥的体积之和为( )
A. B. C. D.
【答案】B
【分析】
作出图形,计算球体的半径,可计算得出两圆锥的高,利用三角形相似计算出圆锥的底面圆半径,再利用锥体体积公式可求得结果.
【详解】
如下图所示,设两个圆锥的底面圆圆心为点,
设圆锥和圆锥的高之比为,即,
设球的半径为,则,可得,所以,,
所以,,,
,则,所以,,
又因为,所以,,
所以,,,
因此,这两个圆锥的体积之和为.
故选:B.
15.(2020·全国·高考真题(理))已知△ABC是面积为的等边三角形,且其顶点都在球O的球面上.若球O的表面积为16π,则O到平面ABC的距离为( )
A. B. C.1 D.
【答案】C
【分析】
根据球的表面积和的面积可求得球的半径和外接圆半径,由球的性质可知所求距离.
【详解】
设球的半径为,则,解得:.
设外接圆半径为,边长为,
是面积为的等边三角形,
,解得:,,
球心到平面的距离.
故选:C.
【点睛】
本题考查球的相关问题的求解,涉及到球的表面积公式和三角形面积公式的应用;解题关键是明确球的性质,即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.
16.(2021·全国·高考真题(理))已如A,B,C是半径为1的球O的球面上的三个点,且,则三棱锥的体积为( )
A. B. C. D.
【答案】A
【分析】
由题可得为等腰直角三角形,得出外接圆的半径,则可求得到平面的距离,进而求得体积.
【详解】
,为等腰直角三角形,,
则外接圆的半径为,又球的半径为1,
设到平面的距离为,
则,
所以.
故选:A.
【点睛】
关键点睛:本题考查球内几何体问题,解题的关键是正确利用截面圆半径、球半径、球心到截面距离的勾股关系求解.
17.(2020·全国·高考真题(理))已知为球的球面上的三个点,⊙为的外接圆,若⊙的面积为,,则球的表面积为( )
A. B. C. D.
【答案】A
【分析】
由已知可得等边的外接圆半径,进而求出其边长,得出的值,根据球的截面性质,求出球的半径,即可得出结论.
【详解】
设圆半径为,球的半径为,依题意,
得,为等边三角形,
由正弦定理可得,
,根据球的截面性质平面,
,
球的表面积.
故选:A
【点睛】
本题考查球的表面积,应用球的截面性质是解题的关键,考查计算求解能力,属于基础题.
18.(2020·海南·高考真题)已知直四棱柱ABCD–A1B1C1D1的棱长均为2,∠BAD=60°.以为球心,为半径的球面与侧面BCC1B1的交线长为________.
【答案】.
【分析】
根据已知条件易得,侧面,可得侧面与球面的交线上的点到的距离为,可得侧面与球面的交线是扇形的弧,再根据弧长公式可求得结果.
【详解】
如图:
取的中点为,的中点为,的中点为,
因为60°,直四棱柱的棱长均为2,所以△为等边三角形,所以,,
又四棱柱为直四棱柱,所以平面,所以,
因为,所以侧面,
设为侧面与球面的交线上的点,则,
因为球的半径为,,所以,
所以侧面与球面的交线上的点到的距离为,
因为,所以侧面与球面的交线是扇形的弧,
因为,所以,
所以根据弧长公式可得.
故答案为:.
【点睛】
本题考查了直棱柱的结构特征,考查了直线与平面垂直的判定,考查了立体几何中的轨迹问题,考查了扇形中的弧长公式,属于中档题.
四、立体几何的数学应用
19.(2021·全国·高考真题)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为(轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O,半径r为的球,其上点A的纬度是指与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为,记卫星信号覆盖地球表面的表面积为(单位:),则S占地球表面积的百分比约为( )
A.26% B.34% C.42% D.50%
【答案】C
【分析】
由题意结合所给的表面积公式和球的表面积公式整理计算即可求得最终结果.
【详解】
由题意可得,S占地球表面积的百分比约为:
.
故选:C.
20.(2021·北京·高考真题)某一时间段内,从天空降落到地面上的雨水,未经蒸发、渗漏、流失而在水平面上积聚的深度,称为这个时段的降雨量(单位:).24h降雨量的等级划分如下:
在综合实践活动中,某小组自制了一个底面直径为200 mm,高为300 mm的圆锥形雨量器.若一次降雨过程中,该雨量器收集的24h的雨水高度是150 mm(如图所示),则这24h降雨量的等级是
A.小雨 B.中雨 C.大雨 D.暴雨
【答案】B
【分析】
计算出圆锥体积,除以圆面的面积即可得降雨量,即可得解.
【详解】
由题意,一个半径为的圆面内的降雨充满一个底面半径为,高为的圆锥,
所以积水厚度,属于中雨.
故选:B.
21.(2020·海南·高考真题)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )
A.20° B.40°
C.50° D.90°
【答案】B
【分析】
画出过球心和晷针所确定的平面截地球和晷面的截面图,根据面面平行的性质定理和线面垂直的定义判定有关截线的关系,根据点处的纬度,计算出晷针与点处的水平面所成角.
【详解】
画出截面图如下图所示,其中是赤道所在平面的截线;是点处的水平面的截线,依题意可知;是晷针所在直线.是晷面的截线,依题意依题意,晷面和赤道平面平行,晷针与晷面垂直,
根据平面平行的性质定理可得可知、根据线面垂直的定义可得..
由于,所以,
由于,
所以,也即晷针与点处的水平面所成角为.
故选:B
【点睛】
本小题主要考查中国古代数学文化,考查球体有关计算,涉及平面平行,线面垂直的性质,属于中档题.
22.(2020·全国·高考真题(理))埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
A. B. C. D.
【答案】C
【分析】
设,利用得到关于的方程,解方程即可得到答案.
【详解】
如图,设,则,
由题意,即,化简得,
解得(负值舍去).
故选:C.
【点晴】
本题主要考查正四棱锥的概念及其有关计算,考查学生的数学计算能力,是一道容易题.
23.(2020·江苏·高考真题)如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm,高为2 cm,内孔半径为0.5 cm,则此六角螺帽毛坯的体积是____cm.
【答案】
【分析】
先求正六棱柱体积,再求圆柱体积,相减得结果.
【详解】
正六棱柱体积为
圆柱体积为
所求几何体体积为
故答案为:
【点睛】
本题考查正六棱柱体积、圆柱体积,考查基本分析求解能力,属基础题.
五、立体几何与空间向量的综合应用
24.(2021·全国·高考真题(理))在正方体中,P为的中点,则直线与所成的角为( )
A. B. C. D.
【答案】D
【分析】
平移直线至,将直线与所成的角转化为与所成的角,解三角形即可.
【详解】
如图,连接,因为∥,
所以或其补角为直线与所成的角,
因为平面,所以,又,,
所以平面,所以,
设正方体棱长为2,则,
,所以.
故选:D
25.(2021·湖南·高考真题)如图,四棱锥中,底面ABCD是矩形,平面ABCD,E为PD的中点.
(1)证明:平面ACE;
(2)设,,直线PB与平面ABCD所成的角为,求四棱锥的体积.
【答案】(1)证明见解析;(2).
【分析】
(1) 连接交于点,连接,由三角形的中位线定理可知,结合线面平行的判定定理可证明平面.
(2)由题意可知,再运用锥体体积公式可求得四棱锥的体积.
【详解】
(1)连接交于点,连接. 在中,因为,
所以,因为平面,平面,则平面.
(2)因为平面ABCD,所以就是直线PB与平面ABCD所成的角,所以,
又,,所以,
所以四棱锥的体积,
所以四棱锥的体积为.
26.(2021·全国·高考真题)在四棱锥中,底面是正方形,若.
(1)证明:平面平面;
(2)求二面角的平面角的余弦值.
【答案】(1)证明见解析;(2).
【分析】
(1)取的中点为,连接,可证平面,从而得到面面.
(2)在平面内,过作,交于,则,建如图所示的空间坐标系,求出平面、平面的法向量后可求二面角的余弦值.
【详解】
(1)取的中点为,连接.
因为,,则,
而,故.
在正方形中,因为,故,故,
因为,故,故为直角三角形且,
因为,故平面,
因为平面,故平面平面.
(2)在平面内,过作,交于,则,
结合(1)中的平面,故可建如图所示的空间坐标系.
则,故.
设平面的法向量,
则即,取,则,
故.
而平面的法向量为,故.
二面角的平面角为锐角,故其余弦值为.
27.(2021·天津·高考真题)如图,在棱长为2的正方体中,E为棱BC的中点,F为棱CD的中点.
(I)求证:平面;
(II)求直线与平面所成角的正弦值.
(III)求二面角的正弦值.
【答案】(I)证明见解析;(II);(III).
【分析】
(I)建立空间直角坐标系,求出及平面的一个法向量,证明,即可得证;
(II)求出,由运算即可得解;
(III)求得平面的一个法向量,由结合同角三角函数的平方关系即可得解.
【详解】
(I)以为原点,分别为轴,建立如图空间直角坐标系,
则,,,,,,,
因为E为棱BC的中点,F为棱CD的中点,所以,,
所以,,,
设平面的一个法向量为,
则,令,则,
因为,所以,
因为平面,所以平面;
(II)由(1)得,,
设直线与平面所成角为,
则;
(III)由正方体的特征可得,平面的一个法向量为,
则,
所以二面角的正弦值为.
28.(2021·全国·高考真题(理))已知直三棱柱中,侧面为正方形,,E,F分别为和的中点,D为棱上的点.
(1)证明:;
(2)当为何值时,面与面所成的二面角的正弦值最小
【答案】(1)见解析;(2)
【分析】
通过已知条件,确定三条互相垂直的直线,建立合适的空间直角坐标系,借助空间向量证明线线垂直和求出二面角的平面角的余弦值最大,进而可以确定出答案.
【详解】
因为三棱柱是直三棱柱,所以底面,所以
因为,,所以,
又,所以平面.
所以两两垂直.
以为坐标原点,分别以所在直线为轴建立空间直角坐标系,如图.
所以,
.
由题设().
(1)因为,
所以,所以.
(2)设平面的法向量为,
因为,
所以,即.
令,则
因为平面的法向量为,
设平面与平面的二面角的平面角为,
则.
当时,取最小值为,
此时取最大值为.
所以,
此时.
【点睛】
本题考查空间向量的相关计算,能够根据题意设出(),在第二问中通过余弦值最大,找到正弦值最小是关键一步.
29.(2021·北京·高考真题)如图:在正方体中,为中点,与平面交于点.
(1)求证:为的中点;
(2)点是棱上一点,且二面角的余弦值为,求的值.
【答案】(1)证明见解析;(2).
【分析】
(1)首先将平面进行扩展,然后结合所得的平面与直线的交点即可证得题中的结论;
(2)建立空间直角坐标系,利用空间直角坐标系求得相应平面的法向量,然后解方程即可求得实数的值.
【详解】
(1)如图所示,取的中点,连结,
由于为正方体,为中点,故,
从而四点共面,即平面CDE即平面,
据此可得:直线交平面于点,
当直线与平面相交时只有唯一的交点,故点与点重合,
即点为中点.
(2)以点为坐标原点,方向分别为轴,轴,轴正方形,建立空间直角坐标系,
不妨设正方体的棱长为2,设,
则:,
从而:,
设平面的法向量为:,则:
,
令可得:,
设平面的法向量为:,则:
,
令可得:,
从而:,
则:,
整理可得:,故(舍去).
【点睛】
本题考查了立体几何中的线面关系和二面角的求解问题,意在考查学生的空间想象能力和逻辑推理能力,对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解.
30.(2020·全国·高考真题(理))如图,为圆锥的顶点,是圆锥底面的圆心,为底面直径,.是底面的内接正三角形,为上一点,.
(1)证明:平面;
(2)求二面角的余弦值.
【答案】(1)证明见解析;(2).
【分析】
(1)要证明平面,只需证明,即可;
(2)以O为坐标原点,OA为x轴,ON为y轴建立如图所示的空间直角坐标系,分别算出平面的法向量为,平面的法向量为,利用公式计算即可得到答案.
【详解】
(1)由题设,知为等边三角形,设,
则,,所以,
又为等边三角形,则,所以,
,则,所以,
同理,又,所以平面;
(2)过O作∥BC交AB于点N,因为平面,以O为坐标原点,OA为x轴,ON为y轴建立如图所示的空间直角坐标系,
则,
,,,
设平面的一个法向量为,
由,得,令,得,
所以,
设平面的一个法向量为
由,得,令,得,
所以
故,
设二面角的大小为,则.
【点晴】
本题主要考查线面垂直的证明以及利用向量求二面角的大小,考查学生空间想象能力,数学运算能力,是一道容易题.
试卷第2页,共31页
试卷第1页,共1页
同课章节目录
