轴对称单元测试卷

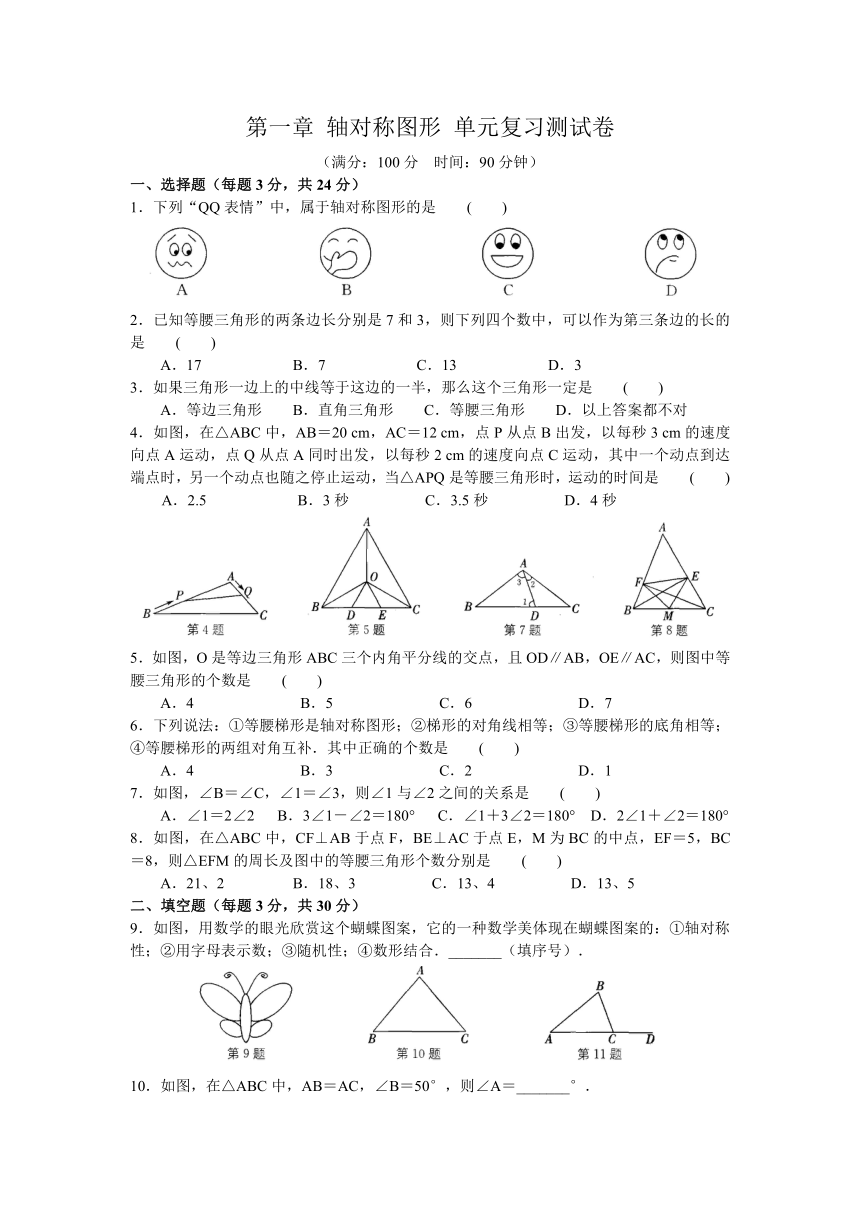
第一章 轴对称图形 单元复习测试卷
（满分：100分 时间：90分钟）
一、选择题（每题3分，共24分）
1．下列“QQ表情”中，属于轴对称图形的是 ( )
2．已知等腰三角形的两条边长分别是7和3，则下列四个数中，可以作为第三条边的长的是 ( )
A．17 　　　　 B．7 　　　　 C．13 　　　　 D．3
3．如果三角形一边上的中线等于这边的一半，那么这个三角形一定是 ( )
A．等边三角形 B．直角三角形 C．等腰三角形 D．以上答案都不对
4．如图，在△ABC中，AB＝20 cm，AC＝12 cm，点P从点B出发，以每秒3 cm的速度向点A运动，点Q从点A同时出发，以每秒2 cm的速度向点C运动，其中一个动点到达端点时，另一个动点也随之停止运动，当△APQ是等腰三角形时，运动的时间是 ( )
A．2.5 　　　　 B．3秒　　　 C．3.5秒 　　　 D．4秒
5．如图，O是等边三角形ABC三个内角平分线的交点，且OD∥AB，OE∥AC，则图中等腰三角形的个数是 ( )
A．4 　　　　　 B．5 　　　　　 C．6 　　　　　 D．7
6．下列说法：①等腰梯形是轴对称图形；②梯形的对角线相等；③等腰梯形的底角相等；④等腰梯形的两组对角互补．其中正确的个数是 ( )
A．4 　　　　　 B．3 　　　　　 C．2 　　　　　 D．1
7．如图，∠B＝∠C，∠1＝∠3，则∠1与∠2之间的关系是 ( )
A．∠1＝2∠2 B．3∠1－∠2＝180° 　C．∠1＋3∠2＝180°　D．2∠1＋∠2＝180°
8．如图，在△ABC中，CF⊥AB于点F，BE⊥AC于点E，M为BC的中点，EF＝5，BC＝8，则△EFM的周长及图中的等腰三角形个数分别是 ( )
A．21、2 　　　 B．18、3 　　　 C．13、4 　　　 D．13、5
二、填空题（每题3分，共30分）
9．如图，用数学的眼光欣赏这个蝴蝶图案，它的一种数学美体现在蝴蝶图案的：①轴对称性；②用字母表示数；③随机性；④数形结合．_______（填序号）．
10．如图，在△ABC中，AB＝AC，∠B＝50°，则∠A＝_______°．
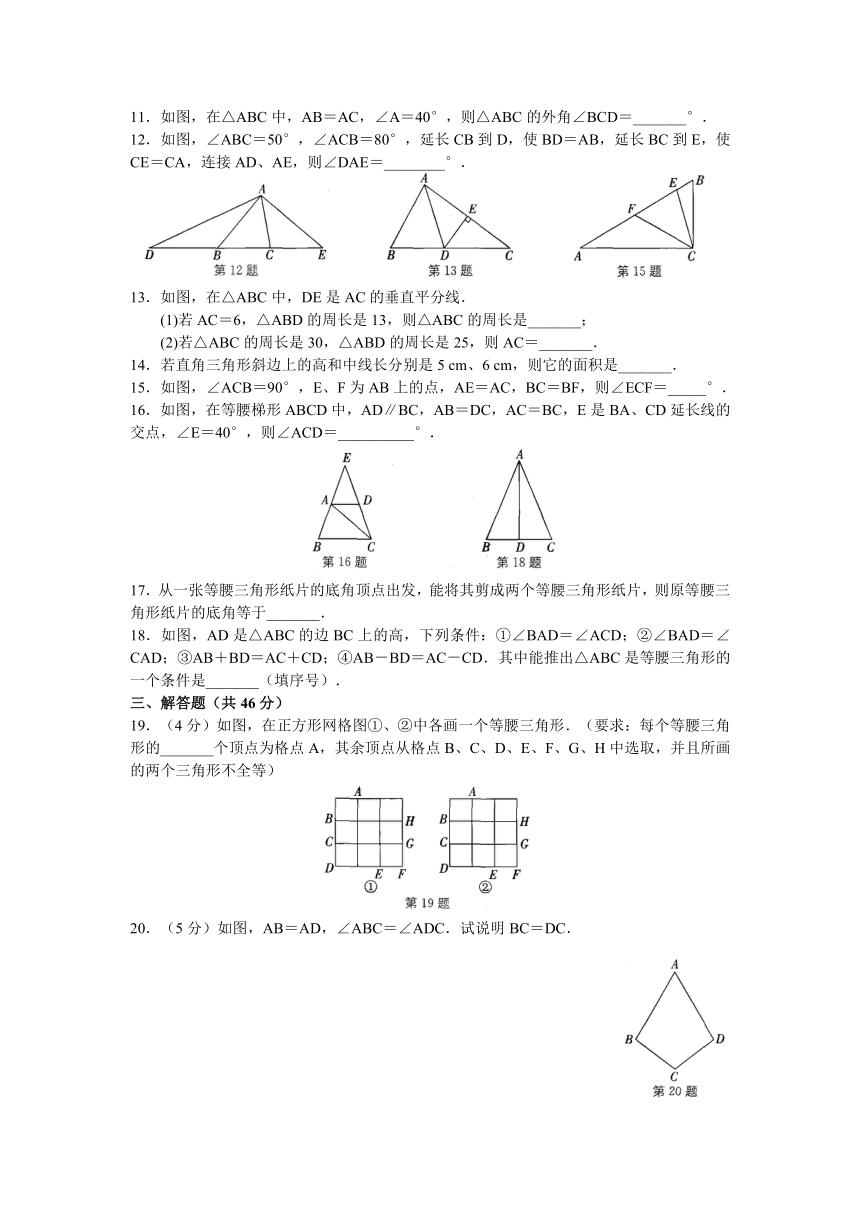
11．如图，在△ABC中，AB＝AC，∠A＝40°，则△ABC的外角∠BCD＝_______°．
12．如图，∠ABC＝50°，∠ACB＝80°，延长CB到D，使BD＝AB，延长BC到E，使CE＝CA，连接AD、AE，则∠DAE＝________°．
13．如图，在△ABC中，DE是AC的垂直平分线．
(1)若AC＝6，△ABD的周长是13，则△ABC的周长是_______；
(2)若△ABC的周长是30，△ABD的周长是25，则AC＝_______．
14．若直角三角形斜边上的高和中线长分别是5 cm、6 cm，则它的面积是_______．
15．如图，∠ACB＝90°，E、F为AB上的点，AE＝AC，BC＝BF，则∠ECF＝_____°．
16．如图，在等腰梯形ABCD中，AD∥BC，AB＝DC，AC＝BC，E是BA、CD延长线的交点，∠E＝40°，则∠ACD＝__________°．
17．从一张等腰三角形纸片的底角顶点出发，能将其剪成两个等腰三角形纸片，则原等腰三角形纸片的底角等于_______．
18．如图，AD是△ABC的边BC上的高，下列条件：①∠BAD＝∠ACD；②∠BAD＝∠CAD；③AB＋BD＝AC＋CD；④AB－BD＝AC－CD．其中能推出△ABC是等腰三角形的一个条件是_______（填序号）．
三、解答题（共46分）
19．（4分）如图，在正方形网格图①、②中各画一个等腰三角形．（要求：每个等腰三角形的_______个顶点为格点A，其余顶点从格点B、C、D、E、F、G、H中选取，并且所画的两个三角形不全等）
20．（5分）如图，AB＝AD，∠ABC＝∠ADC．试说明BC＝DC．
21．（5分）如图，在梯形ABCD中，AD∥BC，AB＝DC＝AD，BC＝AC，求该梯形各内角的度数．
22．（8分）在△ABC中，AC＝BC，∠ACB＝90°，D是AB的中点，E是AB边上一点．
(1)如图①，直线BF垂直于CE于点F，交CD于点G，试说明AE＝CG．
(2)如图②，直线AH垂直于CE，垂足为点H，交CD的延长线于点M，找出图中与BE相等的线段，并说明理由．
23．（8分）如图，在等腰梯形ABCD中，∠C＝60°，AD∥BC，且AD＝DC，E、F分别在AD、DC的延长线上，且DE＝CF．AF、BE交于点P．
(1)试说明AF＝BE．
(2)请你猜测∠BPF的度数，并说明你的结论．
24．（8分）如图，C为线段AB上任意一点（不与A、B重合）分别以AC、BC为一腰在AB的同侧作等腰三角形ACD和等腰三角形BCE，CA＝CD，CB＝CE，∠ACD与∠BCE都是锐角，且∠ACD＝∠BCE，连接AE交CD于点M，连接BD交CE于点N，AE与BD交于点P，连接PC．试说明：
(1)△ACE≌△DCB．
(2)∠APC＝∠BPC．
25．（8分）在△ABC中，AC＝BC，∠ACB＝90°，D、E是AB边上的两点．AD=3，BE=4，∠DCE=45°，则△ABC的面积是多少？
参考答案
一、1．C　2．B 　3．B　4．D　5．D　 6．C　7．B　 8．D
二、9．①　10．80　11．110　12．115　13．(1)19 (2)5　14．30 cm2 　15．45 　16．30 17．72°或()°　18．②③④
三、19．答案不惟一，如图所示
20．略　
21．108°　
22．(1)BE＝CM 　(2)略　
23．(1)略　(2)猜想∠BPF＝120°　
24．略
25．由于△ABC中，AC=BC，∠ACB=90°，设DE=x，则AB=7+x，根据勾股定理，列出关于x方程，解出x，再计算△ABC的面积．△ACE∽△CDE∽△BDC
△ABC的面积是36