北师大版数学九年级上册4.7相似三角形的性质 第1课时 课件(共19张PPT)
文档属性
| 名称 | 北师大版数学九年级上册4.7相似三角形的性质 第1课时 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 601.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 14:32:39 | ||
图片预览




文档简介
(共19张PPT)
《义务教育教科书·数学》北师大版九年级(上册)
§4.7 相似三角形的性质
第一课时
1、什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
复习回顾
三角形中,除了边与角外,还有哪些重要的线段?
高、中线、角平分线
高
角平分线
中线
问题引入
这些几何量在相似三角形中有什么关系呢?
掌握相似三角形的有关性质,并能利用这些性质解决一些简单的问题.
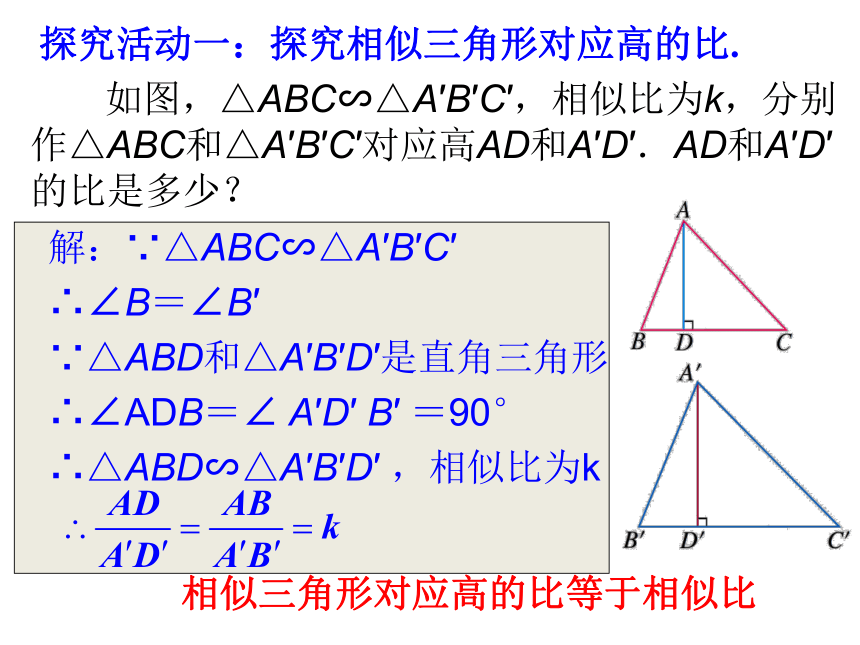
如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应高AD和A′D′.AD和A′D′的比是多少?
解:∵△ABC∽△A′B′C′
∴∠B=∠B′
∵△ABD和△A′B′D′是直角三角形
∴∠ADB=∠ A′D′ B′ =90°
∴△ABD∽△A′B′D′ ,相似比为k
相似三角形对应高的比等于相似比
探究活动一:探究相似三角形对应高的比.
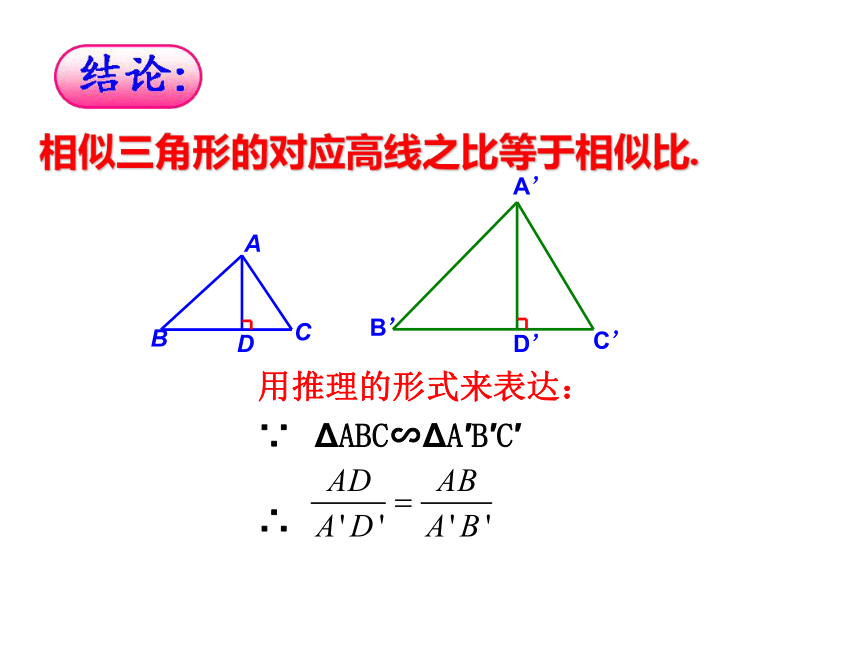
相似三角形的对应高线之比等于相似比.
A
B
C
D
B’
D’
C’
A’
ΔABC∽ΔA′B′C′
∵
∴
用推理的形式来表达:
如图:已知△ABC ∽△A′B′C′,相似比为k,AD平分∠BAC,A’D’平分∠B’A’C’;
E、E’分别为BC、B’C’的中点。
试探究AD与 A’D‘的比值关系,AE与A’E’呢?
探究活动二:
类比探究相似三角形对应中线的比、
对应角平分线的比
A
B
C
D
E
A/
B/
C/
D/
E/
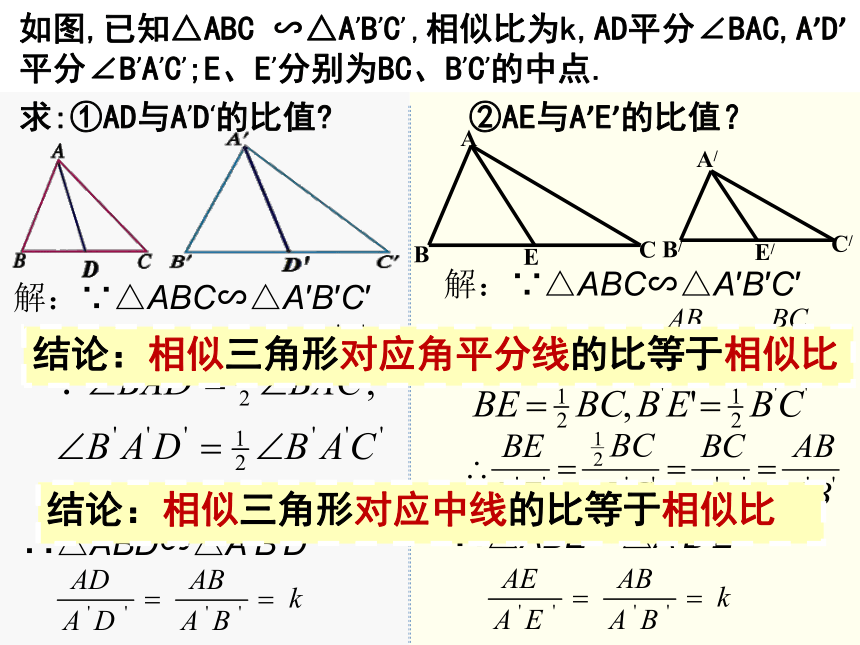
如图,已知△ABC ∽△A’B’C’ ,相似比为k,AD平分∠BAC,A’D’平分∠B’A’C’;E、E’分别为BC、B’C’的中点.
求:①AD与A’D‘的比值 ②AE与A’E’的比值?
A
B
C
E
A/
B/
C/
E/
解:∵△ABC∽△A′B′C′
∴△ABD∽△A′B′D′
解:∵△ABC∽△A′B′C′
∴△ABE∽△A′B′E′
结论:相似三角形对应角平分线的比等于相似比
结论:相似三角形对应中线的比等于相似比
相似三角形性质定理:
相似三角形对应高的比,对应角平分线的比,对应中线的比都等于相似比。
∵△ABC∽△A′B′C′
A
B
C
D
E
A/
B/
C/
D/
E/
F
F‘
如图,已知△ABC ∽△A’B’C’ ,相似比为k,AD平分∠BAC,A’D’平分∠B’A’C’;E、E’分别为BC、B’C’的中点.
求:①AD与A’D‘的比值 ②AE与A’E’的比值?
解:∵△ABC∽△A′B′C′
∴△ABD∽△A′B′D′
解:∵△ABC∽△A′B′C′
∴△ABE∽△A′B′E′
A
B
C
E
A/
B/
C/
E/
B
C
E
A
A/
B/
C/
E/
A
B
C
D
A/
B/
C/
D/
D、E在BC边上.
思考:如果把角平分线、中线变为对应角的n等分线,对应边的n等分线,你能得到哪些结论?
相似三角形对应角的n等分线的比,对应边的n等分线的比都等于相似比。
推广:相似三角形对应线段的比等于相似比
对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形
都等于相似比.
归纳总结:相似三角形的性质
定理 相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比.
(3)如图,DE∥BC,AG⊥BC于G,DE=2,BC=6,AF=1,则AG=_____.
(2)两个相似三角形对应高的比为3∶7,它们的对应角平分线的比为( )
A.7∶3 B.49∶9 C.9∶49 D.3∶7
(1)已知△ABC与△ A′B′C′的相似比为2:3,则对应边上中线之比 ,对应高的比为
,对应角平分线的比为 .
2:3
2:3
2:3
D
3
小试牛刀:
FG=_____.
2
例1 如图,有一块锐角三角形余料ABC,它的边 BC = 12 cm,高 AD = 8 cm . 现要用它裁出一个正方形工件,使正方形的一边在 BC 上,其余的两个顶点分别在 AB,AC 上.
例题
(1)△APN和△ABC相似吗?为什么?
(2)求裁出的正方形的边长.
解∵ SR⊥AD,BC⊥AD,
∴ ∠ASR =∠B,∠ARS=∠C.
∴ △ASR ∽△ABC
∴ SR∥BC.
例2:如图 3-32,AD 是 △ABC 的高,AD = h,点 R 在 AC 边上,点 S 在 AB 边上,SR ⊥ AD,垂足为 E.
当 SR= BC 时,求 DE 的长.如果 SR= BC 呢?
变式练习:
若四边形PQMN为矩形,边BC=12cm,高AD=8cm,
且PN:PQ=2:1,
求矩形PQMN的周长。
填一填
1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.
2∶ 3
2 ∶ 3
2.两个相似三角形的相似比为1:4, 则对应高的比为_________,对应角的角平分线的比为_________.
1:4
1:4
3.两个相似三角形对应中线的比为 ,
则相似比为______,对应高的比为______ .
如图,△ABC中,边BC=12cm,高AD=6cm,
边长为x的正方形PQMN的一边在BC上,其余
两个顶点分别在AB、AC上,则正方形边长x为( )
A.3cm
B.4cm
C.5cm
D.6cm
拓展训练1
如图,△ABC是一张锐角三角形的硬纸片.AD是
边BC上的高,BC=40cm,AD=30cm.
从这张硬纸片剪下一个长HG是宽HE的2倍的矩形
EFGH.使它的一边EF在BC上,顶点G,H分别在AC,
AB上.AD与HG的交点为M.
(1)求证:
(2)求这个矩形EFGH的周长.
拓展训练2
性质定理:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
对应边的比
相似比k
对应高的比
对应中线的比
对应角平分线的比
=
相似三角形
……
推广:相似三角形对应线段的比等于相似比.
通过本节课的学习,你在知识上和方法上有哪些收获?请说说看
《义务教育教科书·数学》北师大版九年级(上册)
§4.7 相似三角形的性质
第一课时
1、什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
复习回顾
三角形中,除了边与角外,还有哪些重要的线段?
高、中线、角平分线
高
角平分线
中线
问题引入
这些几何量在相似三角形中有什么关系呢?
掌握相似三角形的有关性质,并能利用这些性质解决一些简单的问题.
如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应高AD和A′D′.AD和A′D′的比是多少?
解:∵△ABC∽△A′B′C′
∴∠B=∠B′
∵△ABD和△A′B′D′是直角三角形
∴∠ADB=∠ A′D′ B′ =90°
∴△ABD∽△A′B′D′ ,相似比为k
相似三角形对应高的比等于相似比
探究活动一:探究相似三角形对应高的比.
相似三角形的对应高线之比等于相似比.
A
B
C
D
B’
D’
C’
A’
ΔABC∽ΔA′B′C′
∵
∴
用推理的形式来表达:
如图:已知△ABC ∽△A′B′C′,相似比为k,AD平分∠BAC,A’D’平分∠B’A’C’;
E、E’分别为BC、B’C’的中点。
试探究AD与 A’D‘的比值关系,AE与A’E’呢?
探究活动二:
类比探究相似三角形对应中线的比、
对应角平分线的比
A
B
C
D
E
A/
B/
C/
D/
E/
如图,已知△ABC ∽△A’B’C’ ,相似比为k,AD平分∠BAC,A’D’平分∠B’A’C’;E、E’分别为BC、B’C’的中点.
求:①AD与A’D‘的比值 ②AE与A’E’的比值?
A
B
C
E
A/
B/
C/
E/
解:∵△ABC∽△A′B′C′
∴△ABD∽△A′B′D′
解:∵△ABC∽△A′B′C′
∴△ABE∽△A′B′E′
结论:相似三角形对应角平分线的比等于相似比
结论:相似三角形对应中线的比等于相似比
相似三角形性质定理:
相似三角形对应高的比,对应角平分线的比,对应中线的比都等于相似比。
∵△ABC∽△A′B′C′
A
B
C
D
E
A/
B/
C/
D/
E/
F
F‘
如图,已知△ABC ∽△A’B’C’ ,相似比为k,AD平分∠BAC,A’D’平分∠B’A’C’;E、E’分别为BC、B’C’的中点.
求:①AD与A’D‘的比值 ②AE与A’E’的比值?
解:∵△ABC∽△A′B′C′
∴△ABD∽△A′B′D′
解:∵△ABC∽△A′B′C′
∴△ABE∽△A′B′E′
A
B
C
E
A/
B/
C/
E/
B
C
E
A
A/
B/
C/
E/
A
B
C
D
A/
B/
C/
D/
D、E在BC边上.
思考:如果把角平分线、中线变为对应角的n等分线,对应边的n等分线,你能得到哪些结论?
相似三角形对应角的n等分线的比,对应边的n等分线的比都等于相似比。
推广:相似三角形对应线段的比等于相似比
对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形
都等于相似比.
归纳总结:相似三角形的性质
定理 相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比.
(3)如图,DE∥BC,AG⊥BC于G,DE=2,BC=6,AF=1,则AG=_____.
(2)两个相似三角形对应高的比为3∶7,它们的对应角平分线的比为( )
A.7∶3 B.49∶9 C.9∶49 D.3∶7
(1)已知△ABC与△ A′B′C′的相似比为2:3,则对应边上中线之比 ,对应高的比为
,对应角平分线的比为 .
2:3
2:3
2:3
D
3
小试牛刀:
FG=_____.
2
例1 如图,有一块锐角三角形余料ABC,它的边 BC = 12 cm,高 AD = 8 cm . 现要用它裁出一个正方形工件,使正方形的一边在 BC 上,其余的两个顶点分别在 AB,AC 上.
例题
(1)△APN和△ABC相似吗?为什么?
(2)求裁出的正方形的边长.
解∵ SR⊥AD,BC⊥AD,
∴ ∠ASR =∠B,∠ARS=∠C.
∴ △ASR ∽△ABC
∴ SR∥BC.
例2:如图 3-32,AD 是 △ABC 的高,AD = h,点 R 在 AC 边上,点 S 在 AB 边上,SR ⊥ AD,垂足为 E.
当 SR= BC 时,求 DE 的长.如果 SR= BC 呢?
变式练习:
若四边形PQMN为矩形,边BC=12cm,高AD=8cm,
且PN:PQ=2:1,
求矩形PQMN的周长。
填一填
1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.
2∶ 3
2 ∶ 3
2.两个相似三角形的相似比为1:4, 则对应高的比为_________,对应角的角平分线的比为_________.
1:4
1:4
3.两个相似三角形对应中线的比为 ,
则相似比为______,对应高的比为______ .
如图,△ABC中,边BC=12cm,高AD=6cm,
边长为x的正方形PQMN的一边在BC上,其余
两个顶点分别在AB、AC上,则正方形边长x为( )
A.3cm
B.4cm
C.5cm
D.6cm
拓展训练1
如图,△ABC是一张锐角三角形的硬纸片.AD是
边BC上的高,BC=40cm,AD=30cm.
从这张硬纸片剪下一个长HG是宽HE的2倍的矩形
EFGH.使它的一边EF在BC上,顶点G,H分别在AC,
AB上.AD与HG的交点为M.
(1)求证:
(2)求这个矩形EFGH的周长.
拓展训练2
性质定理:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
对应边的比
相似比k
对应高的比
对应中线的比
对应角平分线的比
=
相似三角形
……
推广:相似三角形对应线段的比等于相似比.
通过本节课的学习,你在知识上和方法上有哪些收获?请说说看
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
