15.1 轴对称图形同步练习(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
绝密★启用前
15.1轴对称图形同步练习沪科版初中数学八年级上册
学校:___________姓名:___________班级:___________考号:___________
注意:本试卷包含Ⅰ、Ⅱ_??¤??·???????????·_为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。21世纪教育网版权所有
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分)
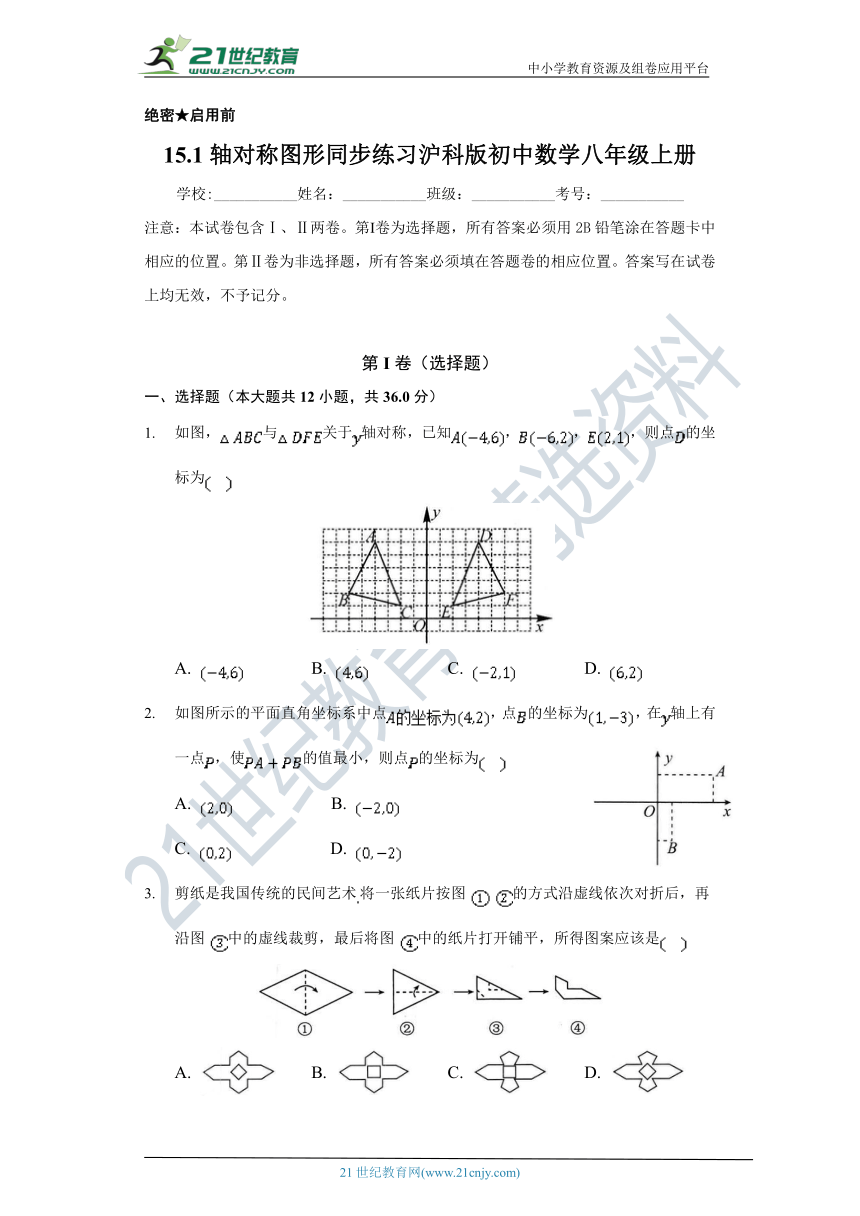
如图,与关于轴对称,已知,,,则点的坐标为????
A. B. C. D.
如图所示的平面直角坐标系中点,点的坐标为,在轴上有一点,使的值最小,则点的坐标为????21教育网
A. B.
C. D.
剪纸是我国传统的民间艺将一张纸片按图的方式沿虚线依次对折后,再沿图中的虚线裁剪,最后将图中的纸片打开铺平,所得图案应该是????
A. B. C. D.
已知点,,把线段向右平移个单位得到线段,则下列关于线段与线段的位置关系描述最准确的是????21·cn·jy·com
A. 互相垂直 B. 关于轴对称
C. 关于轴对称 D. 互相平行且关于轴对称
如图,点在直线上,关于直线对称,连接分别交,于点,,连接,下列结论不一定正确的是????www.21-cn-jy.com
A. B.
C. D.
如图,关于直线进行轴对称变换后得到,下列说法中不正确的是????
A. ,
B. 直线垂直平分,
C. 和均是等腰三角形
D. ,
图中序号,,,对应的四个三角形,都是这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是????2·1·c·n·j·y
A. B. C. D.
如图所示的各组图形中的两个小狗,成轴对称的是????
A. B. C. D.
下列图形中所有轴对称图形的对称轴条数之和为????
A. B. C. D.
如图的的_??????????????????_,的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与成轴对称的格点三角形一共有????21·世纪*教育网
A. 个 B. 个 C. 个 D. 个
如图,在中,,于点,,,则? ?
A. B. C. D.
若直线经过点,直线经过点,且与关于轴对称,则与的交点的坐标为????
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共5小题,共15.0分)
小强站在镜前,从镜中看到镜子对面墙上挂着的电子表读数如图,则电子表上的实际时间是??????????.www-2-1-cnjy-com
如图,把一张长沿折叠,点,分别落在点,的位置上,交于点,已知,那么??????????.
21cnjy.com
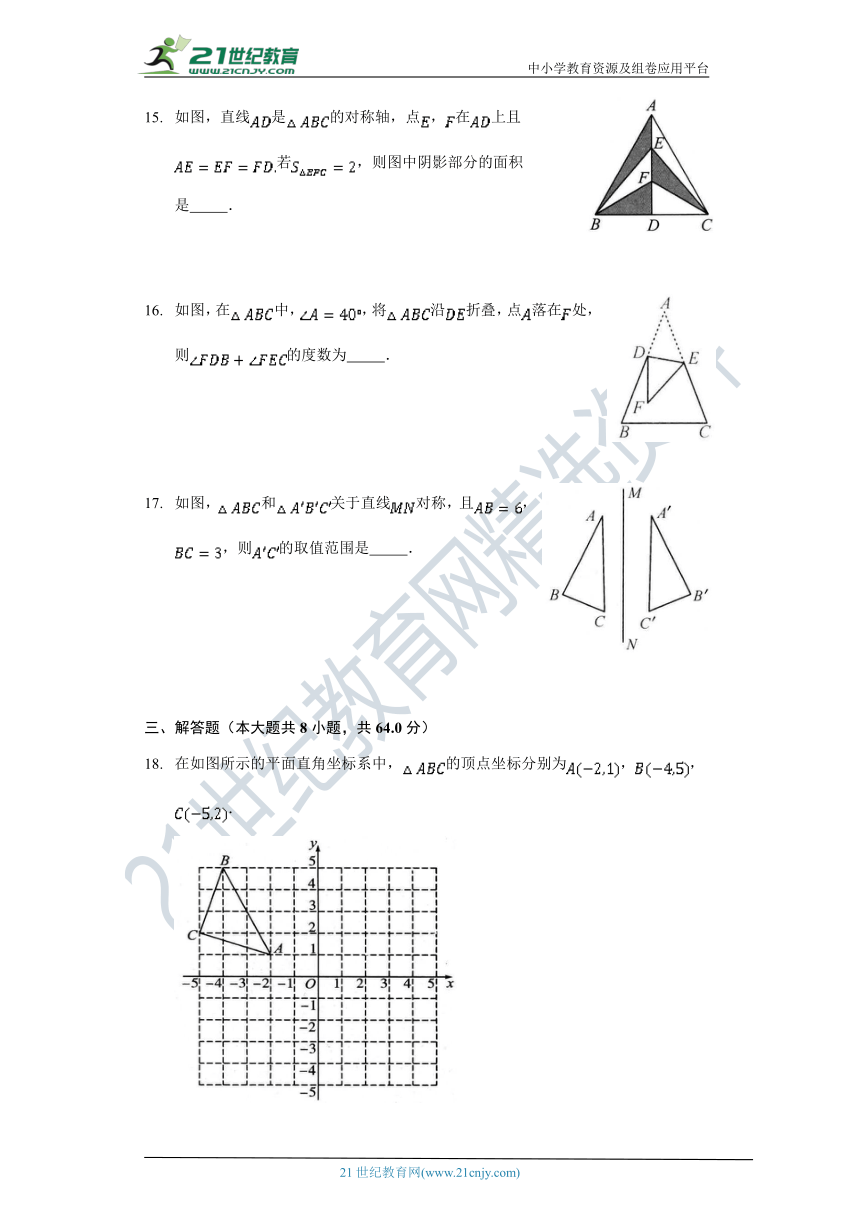
如图,直线的对称轴,点,在上且若,则图中阴影部分的面积是??????????.
如图,在中,,将沿折叠,点落在处,则的度数为??????????.
如图,和关于直线对称,且,,则的取值范围是??????????.
三、解答题(本大题共8小题,共64.0分)
在如图所示的平面直角坐标系中,的顶点坐标分别为,,.
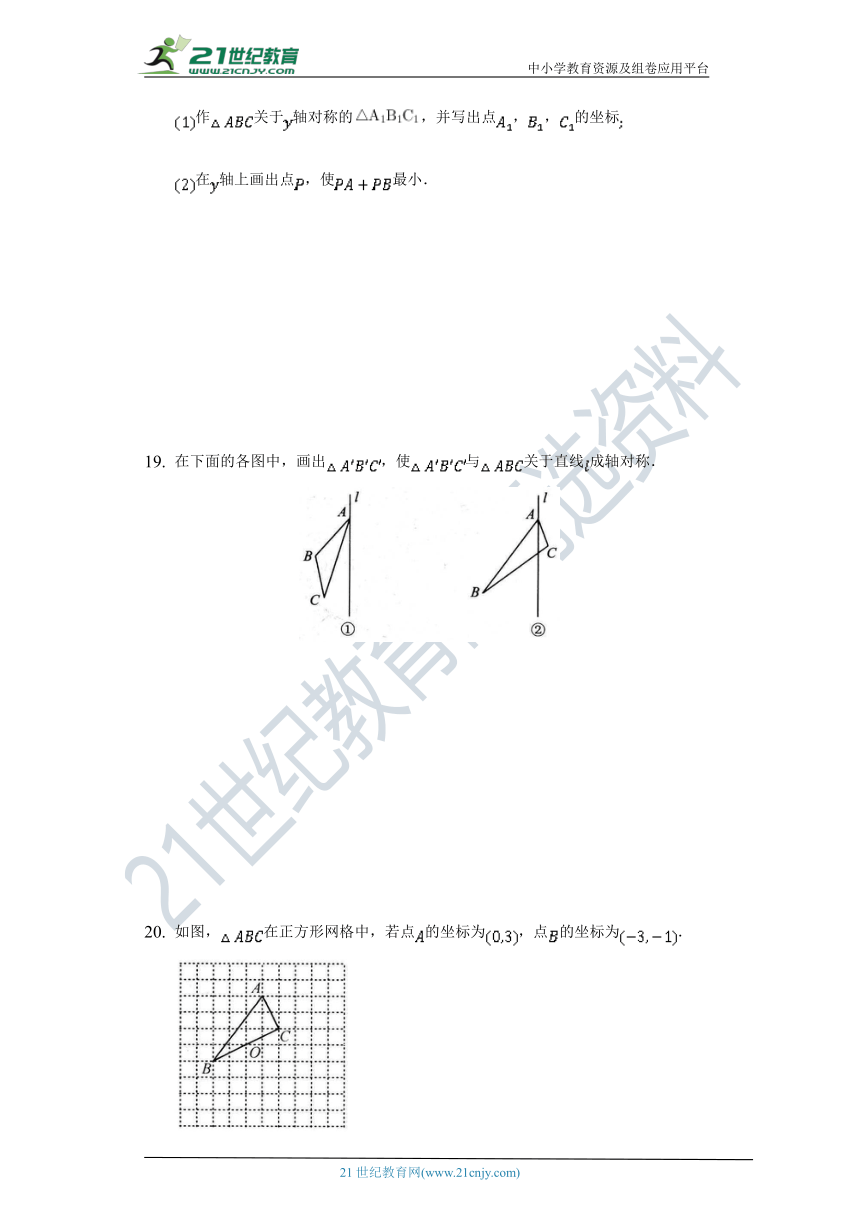
作关于轴对称的,并写出点,,的坐标
在轴上画出点,使最小.
在下面的各图中,画出,使与关于直线成轴对称.
如图,在正方形网格中,若点的坐标为,点的坐标为.
在图中建立平面直角坐标系
作出关于轴对称的图形,并直接写出点的坐标.
如图,要在一条笔直上建一个燃气站,向同侧的,两个城镇分别铺设管道输送燃气试确定燃气站的位置,使铺设管道的路线最短.
如果在,两个城镇之间规划一个生态保护区图,燃气管道不能穿过该区域,试确定燃气站的位置,使铺设管道的路线最短.2-1-c-n-j-y
如图,在的网格中,每个小正方形的边长都为,网格中有两个格点,和直线.
求作点关于直线的对称点
为直线上一点,连接,,使的周长最小,试确定点的位置.
如图,在中,其中,,.
画出与关于轴对称的
写出各顶点的坐标
求的面积.
如图,已知,,和相交于点求证:.
如图,和是由分别沿着边、翻折得到的若,求的度数.
答案和解析
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
【解析】解:? ?,,?,
,,,,,
,故选 C.
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】
18.【答案】解:如图所示,即为所求;,,.
点如图所示.
19.【答案】解:如图,为所作;
如图,为所作.
20.【答案】解:如图,平面直角坐标系如图所示:
如图,即为所求作,点的坐标.
21.【答案】解:如图
如图
22.【答案】解:如图,
的周长的最小值,
,,
的周长的最小值为.
23.【答案】解:如图,
,,?
.
24.【答案】证明:,,,
.
.
,
.
.
.
25.【答案,
设,则,.
的内角和为,
?,解得.
,.
?和是由分别沿着边、翻折得到的,
,.
?.
、的内角和均为,,,
.
_21?????????è?????(www.21cnjy.com)_
绝密★启用前
15.1轴对称图形同步练习沪科版初中数学八年级上册
学校:___________姓名:___________班级:___________考号:___________
注意:本试卷包含Ⅰ、Ⅱ_??¤??·???????????·_为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。21世纪教育网版权所有
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分)
如图,与关于轴对称,已知,,,则点的坐标为????
A. B. C. D.
如图所示的平面直角坐标系中点,点的坐标为,在轴上有一点,使的值最小,则点的坐标为????21教育网
A. B.
C. D.
剪纸是我国传统的民间艺将一张纸片按图的方式沿虚线依次对折后,再沿图中的虚线裁剪,最后将图中的纸片打开铺平,所得图案应该是????
A. B. C. D.
已知点,,把线段向右平移个单位得到线段,则下列关于线段与线段的位置关系描述最准确的是????21·cn·jy·com
A. 互相垂直 B. 关于轴对称
C. 关于轴对称 D. 互相平行且关于轴对称
如图,点在直线上,关于直线对称,连接分别交,于点,,连接,下列结论不一定正确的是????www.21-cn-jy.com
A. B.
C. D.
如图,关于直线进行轴对称变换后得到,下列说法中不正确的是????
A. ,
B. 直线垂直平分,
C. 和均是等腰三角形
D. ,
图中序号,,,对应的四个三角形,都是这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是????2·1·c·n·j·y
A. B. C. D.
如图所示的各组图形中的两个小狗,成轴对称的是????
A. B. C. D.
下列图形中所有轴对称图形的对称轴条数之和为????
A. B. C. D.
如图的的_??????????????????_,的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与成轴对称的格点三角形一共有????21·世纪*教育网
A. 个 B. 个 C. 个 D. 个
如图,在中,,于点,,,则? ?
A. B. C. D.
若直线经过点,直线经过点,且与关于轴对称,则与的交点的坐标为????
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共5小题,共15.0分)
小强站在镜前,从镜中看到镜子对面墙上挂着的电子表读数如图,则电子表上的实际时间是??????????.www-2-1-cnjy-com
如图,把一张长沿折叠,点,分别落在点,的位置上,交于点,已知,那么??????????.
21cnjy.com
如图,直线的对称轴,点,在上且若,则图中阴影部分的面积是??????????.
如图,在中,,将沿折叠,点落在处,则的度数为??????????.
如图,和关于直线对称,且,,则的取值范围是??????????.
三、解答题(本大题共8小题,共64.0分)
在如图所示的平面直角坐标系中,的顶点坐标分别为,,.
作关于轴对称的,并写出点,,的坐标
在轴上画出点,使最小.
在下面的各图中,画出,使与关于直线成轴对称.
如图,在正方形网格中,若点的坐标为,点的坐标为.
在图中建立平面直角坐标系
作出关于轴对称的图形,并直接写出点的坐标.
如图,要在一条笔直上建一个燃气站,向同侧的,两个城镇分别铺设管道输送燃气试确定燃气站的位置,使铺设管道的路线最短.
如果在,两个城镇之间规划一个生态保护区图,燃气管道不能穿过该区域,试确定燃气站的位置,使铺设管道的路线最短.2-1-c-n-j-y
如图,在的网格中,每个小正方形的边长都为,网格中有两个格点,和直线.
求作点关于直线的对称点
为直线上一点,连接,,使的周长最小,试确定点的位置.
如图,在中,其中,,.
画出与关于轴对称的
写出各顶点的坐标
求的面积.
如图,已知,,和相交于点求证:.
如图,和是由分别沿着边、翻折得到的若,求的度数.
答案和解析
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
【解析】解:? ?,,?,
,,,,,
,故选 C.
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】
18.【答案】解:如图所示,即为所求;,,.
点如图所示.
19.【答案】解:如图,为所作;
如图,为所作.
20.【答案】解:如图,平面直角坐标系如图所示:
如图,即为所求作,点的坐标.
21.【答案】解:如图
如图
22.【答案】解:如图,
的周长的最小值,
,,
的周长的最小值为.
23.【答案】解:如图,
,,?
.
24.【答案】证明:,,,
.
.
,
.
.
.
25.【答案,
设,则,.
的内角和为,
?,解得.
,.
?和是由分别沿着边、翻折得到的,
,.
?.
、的内角和均为,,,
.
_21?????????è?????(www.21cnjy.com)_
