八年级数学11.3.1角平分线的性质
文档属性
| 名称 | 八年级数学11.3.1角平分线的性质 |
|
|
| 格式 | zip | ||
| 文件大小 | 171.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-24 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
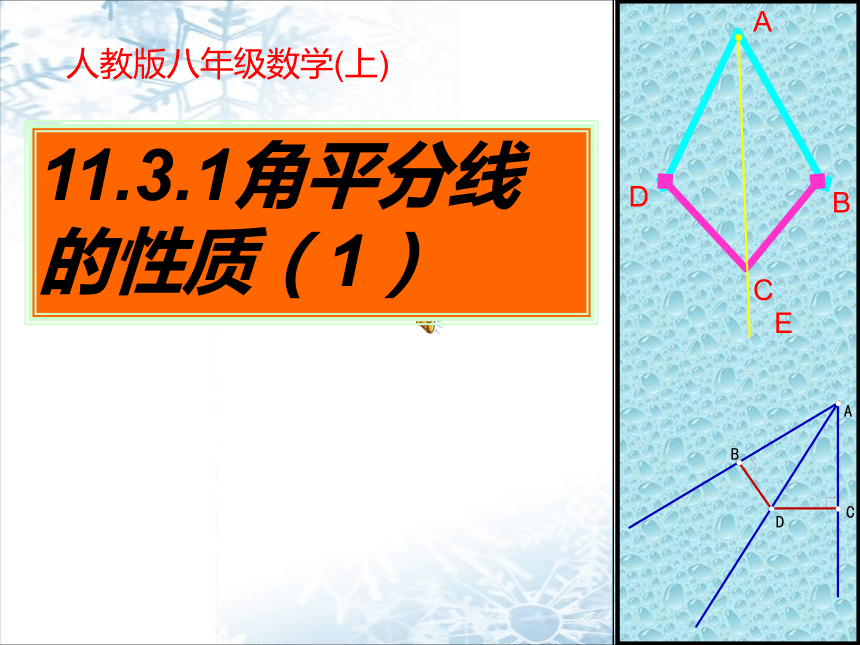
人教版八年级数学(上)
11.3.1角平分线的性质(1)
A
D
B
C
E
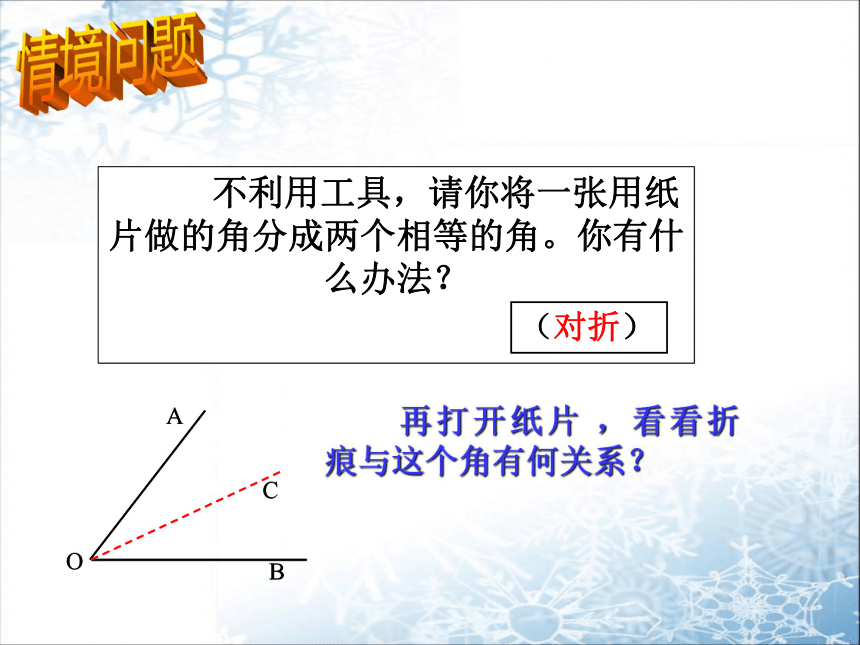
不利用工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?
A
O
B
C
再打开纸片 ,看看折痕与这个角有何关系?
(对折)
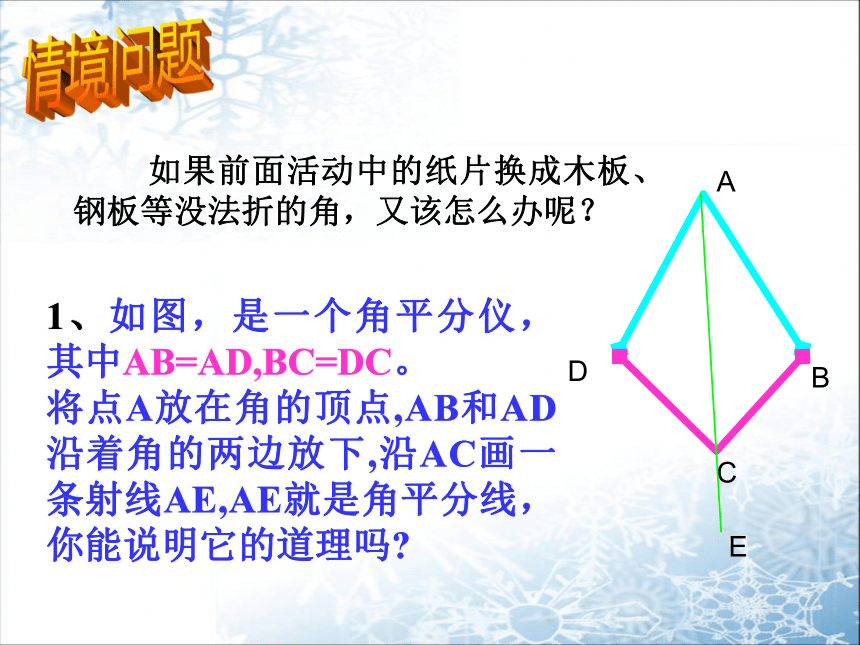
1、如图,是一个角平分仪,其中AB=AD,BC=DC。
将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗
A
D
B
C
E
如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?
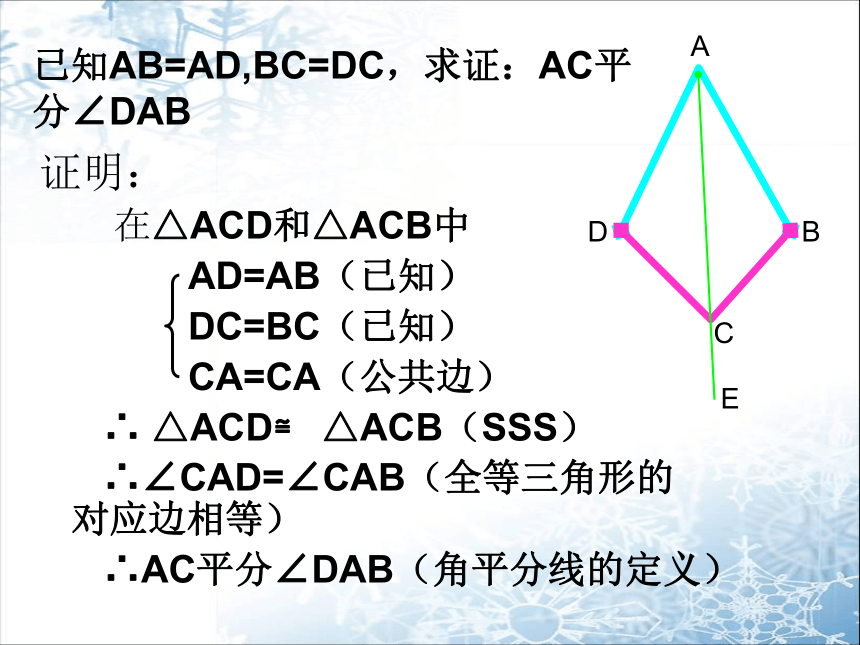
证明:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴ △ACD≌ △ACB(SSS)
∴∠CAD=∠CAB(全等三角形的 对应边相等)
∴AC平分∠DAB(角平分线的定义)
A
D
B
C
E
已知AB=AD,BC=DC,求证:AC平 分∠DAB
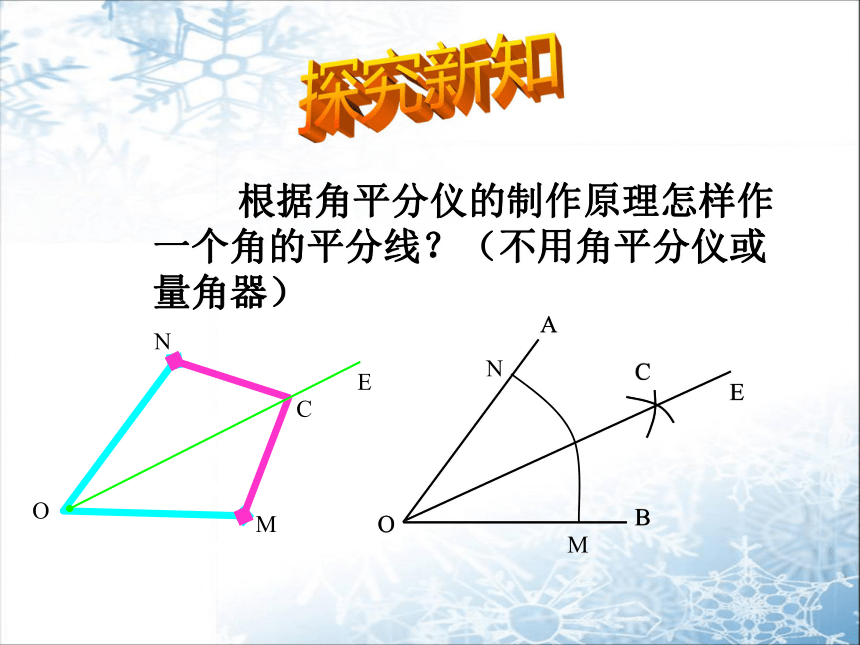
根据角平分仪的制作原理怎样作一个角的平分线?(不用角平分仪或量角器)
O
A
B
C
E
N
O
M
C
E
N
M
用尺子和圆规作角的平分线
已知:∠AOB
求作: ∠AOB的平分线.
作法:
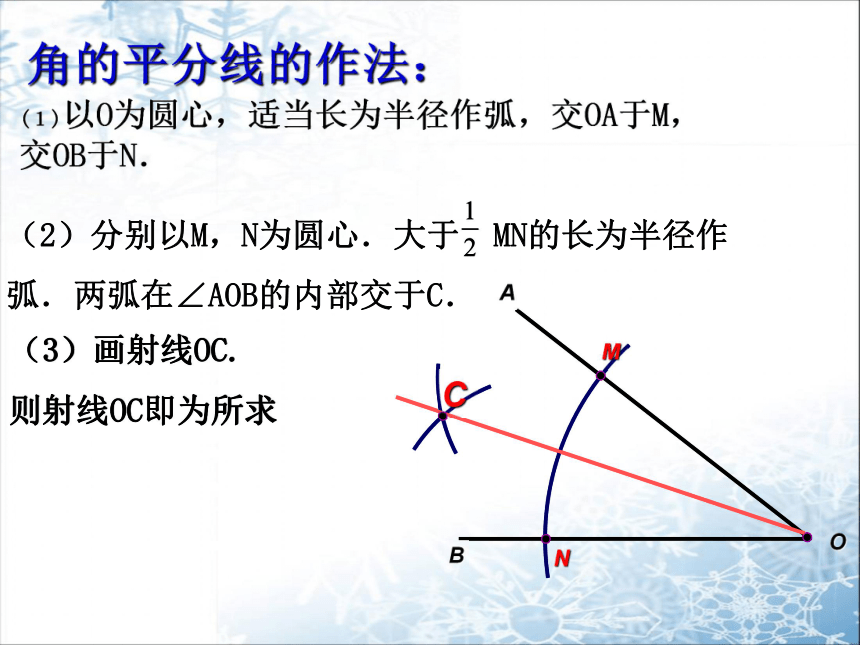
角的平分线的作法:
(3)画射线OC.
则射线OC即为所求
A
B
O
M
N
C
(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
(2)分别以M,N为圆心.大于 MN的长为半径作弧.两弧在∠AOB的内部交于C.
1〉平分平角∠AOB
2〉通过上面的步骤,得到射线OC以后,把它反向延长得到直线CD,直线CD与直线AB是什么关系?
3〉结论:作平角的平分线即可平分平角,由此也得到过直线上一点作这条直线的垂线的方法。
A
B
O
C
D
探究角平分线的性质
(1)实验:将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
(2)猜想:角的平分线上的点到角的两边的距离相等.
P
A
O
B
C
E
D
1
2
已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E
求证: PD=PE
(3)验证猜想
(4)得出结论:
角平分线的性质:角平分线上的点到角两 边的距离相等。
(那么红色线标出的是不是也相等呢,为什么?)
思考:
要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺 1:20 000)
S
O
公路
铁路
要在S区建立一个集贸市场,使它到公路、铁路的距离相等,小明工程师说这个集贸市场一定位于公路与铁路夹角的平分线上。(如图示)你觉得小明说的对吗?为什么?
s
已知夹角∠AOB,求证:到角∠AOB两边的距离相等的点在角平分线上
怎样转化成数学语言呢?
P
A
O
B
C
E
D
1
2
已知∠AOB,PD⊥OA于点D,PE⊥OB于点E, PD=PE,点P在OC上, 求证:OC平分∠AOB
由此可以得到:角的内部到角的两边的距离相等的点在角平分线上
如图:在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF; 求证:CF=EB
A
C
D
E
B
F
用尺规作角的平分线.
定理 角平分线上的点到这个角的两边距离相等.
角的内部到角的两边的距离相等的点在角的平分线上。
小结
人教版八年级数学(上)
11.3.1角平分线的性质(1)
A
D
B
C
E
不利用工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?
A
O
B
C
再打开纸片 ,看看折痕与这个角有何关系?
(对折)
1、如图,是一个角平分仪,其中AB=AD,BC=DC。
将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗
A
D
B
C
E
如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?
证明:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴ △ACD≌ △ACB(SSS)
∴∠CAD=∠CAB(全等三角形的 对应边相等)
∴AC平分∠DAB(角平分线的定义)
A
D
B
C
E
已知AB=AD,BC=DC,求证:AC平 分∠DAB
根据角平分仪的制作原理怎样作一个角的平分线?(不用角平分仪或量角器)
O
A
B
C
E
N
O
M
C
E
N
M
用尺子和圆规作角的平分线
已知:∠AOB
求作: ∠AOB的平分线.
作法:
角的平分线的作法:
(3)画射线OC.
则射线OC即为所求
A
B
O
M
N
C
(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
(2)分别以M,N为圆心.大于 MN的长为半径作弧.两弧在∠AOB的内部交于C.
1〉平分平角∠AOB
2〉通过上面的步骤,得到射线OC以后,把它反向延长得到直线CD,直线CD与直线AB是什么关系?
3〉结论:作平角的平分线即可平分平角,由此也得到过直线上一点作这条直线的垂线的方法。
A
B
O
C
D
探究角平分线的性质
(1)实验:将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
(2)猜想:角的平分线上的点到角的两边的距离相等.
P
A
O
B
C
E
D
1
2
已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E
求证: PD=PE
(3)验证猜想
(4)得出结论:
角平分线的性质:角平分线上的点到角两 边的距离相等。
(那么红色线标出的是不是也相等呢,为什么?)
思考:
要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺 1:20 000)
S
O
公路
铁路
要在S区建立一个集贸市场,使它到公路、铁路的距离相等,小明工程师说这个集贸市场一定位于公路与铁路夹角的平分线上。(如图示)你觉得小明说的对吗?为什么?
s
已知夹角∠AOB,求证:到角∠AOB两边的距离相等的点在角平分线上
怎样转化成数学语言呢?
P
A
O
B
C
E
D
1
2
已知∠AOB,PD⊥OA于点D,PE⊥OB于点E, PD=PE,点P在OC上, 求证:OC平分∠AOB
由此可以得到:角的内部到角的两边的距离相等的点在角平分线上
如图:在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF; 求证:CF=EB
A
C
D
E
B
F
用尺规作角的平分线.
定理 角平分线上的点到这个角的两边距离相等.
角的内部到角的两边的距离相等的点在角的平分线上。
小结
