湖南省永州市冷水滩区2021-2022学年九年级上学期期中考试数学试题(word版 含答案)
文档属性
| 名称 | 湖南省永州市冷水滩区2021-2022学年九年级上学期期中考试数学试题(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 121.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 11:02:45 | ||
图片预览


文档简介
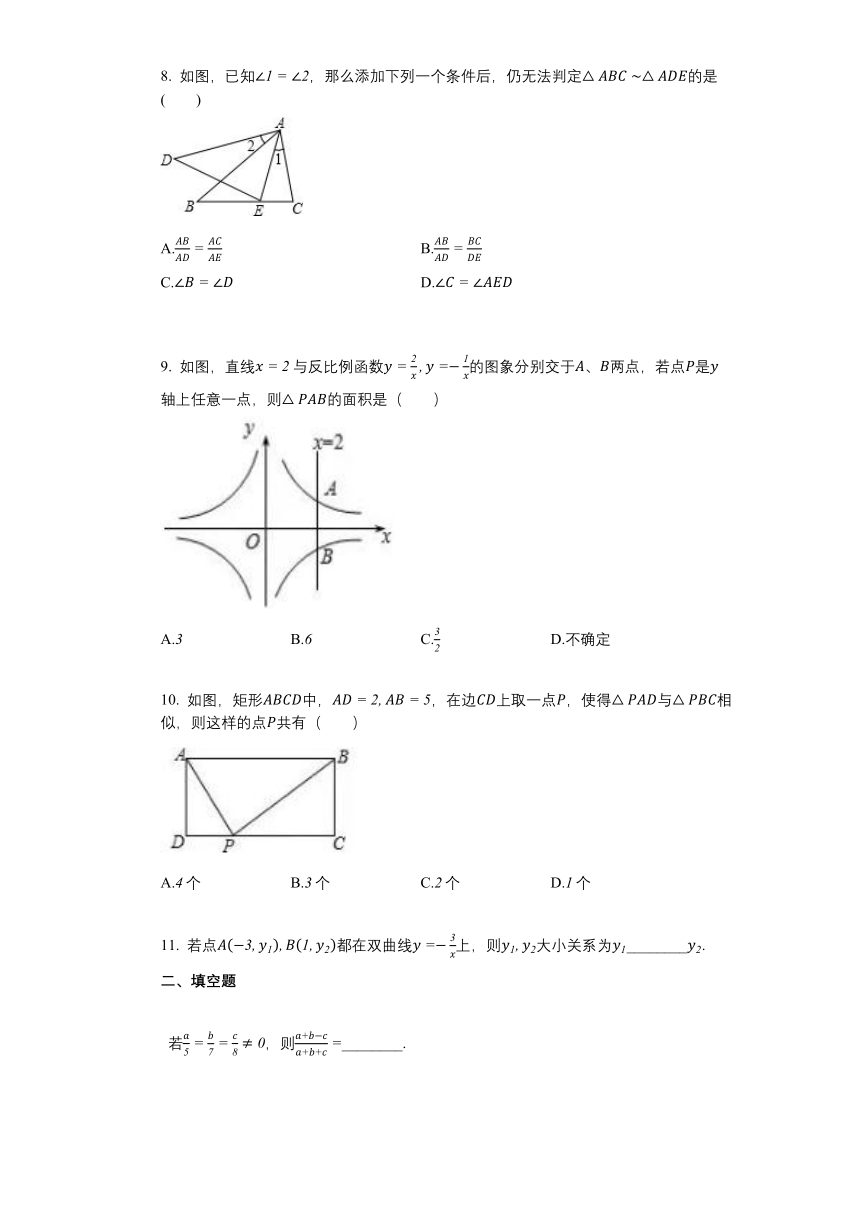
2021-2022学年湖南省永州市初三(上)期中考试数学试卷
一、选择题
1. 下列方程是一元二次方程的是( )
A. B. C. D.
2. 关于反比例函数,下列说法不正确的是( )
A.图象经过 B.图象位于一、三象限
C.图象关于直线对称 D.随的增大而增大
3. 已知是方程的两根,则的值为( )
A. B. C. D.
4. 如图,在 中,,,,则的长为( )
A. B. C. D.
5. 在同一坐标系中,函数和的图象大致是( )
A. B. C. D.
6. 已知与是位似三角形,且,则与的周长之比为( )
A. B. C. D.
7. 永州市年底城市绿地面积是万平方米,计划到年底城市绿地面积提高到万平方米,则平均每年的增长率为( )
A. B. C. D.
8. 如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B.
C. D.
9. 如图,直线与反比例函数的图象分别交于、两点,若点是轴上任意一点,则的面积是( )
A. B. C. D.不确定
10. 如图,矩形中,,在边上取一点,使得与相似,则这样的点共有( )
A.个 B.个 C.个 D.个
11. 若点都在双曲线上,则大小关系为________.
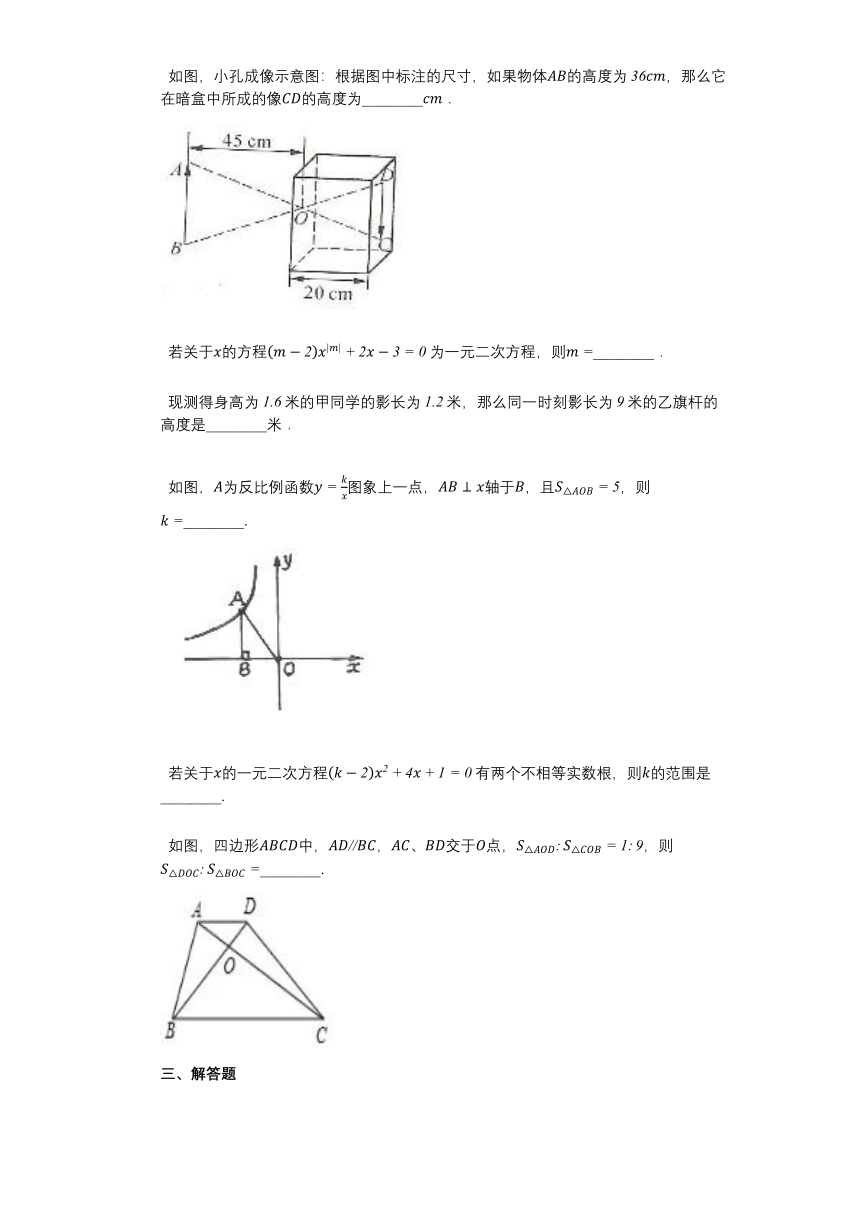
二、填空题
若,则________.
如图,小孔成像示意图:根据图中标注的尺寸,如果物体的高度为,那么它在暗盒中所成的像的高度为________.
若关于的方程为一元二次方程,则________.
现测得身高为米的甲同学的影长为米,那么同一时刻影长为米的乙旗杆的高度是________米.
如图,为反比例函数图象上一点,轴于,且,则________.
若关于的一元二次方程有两个不相等实数根,则的范围是________.
如图,四边形中,,、交于点,,则________.
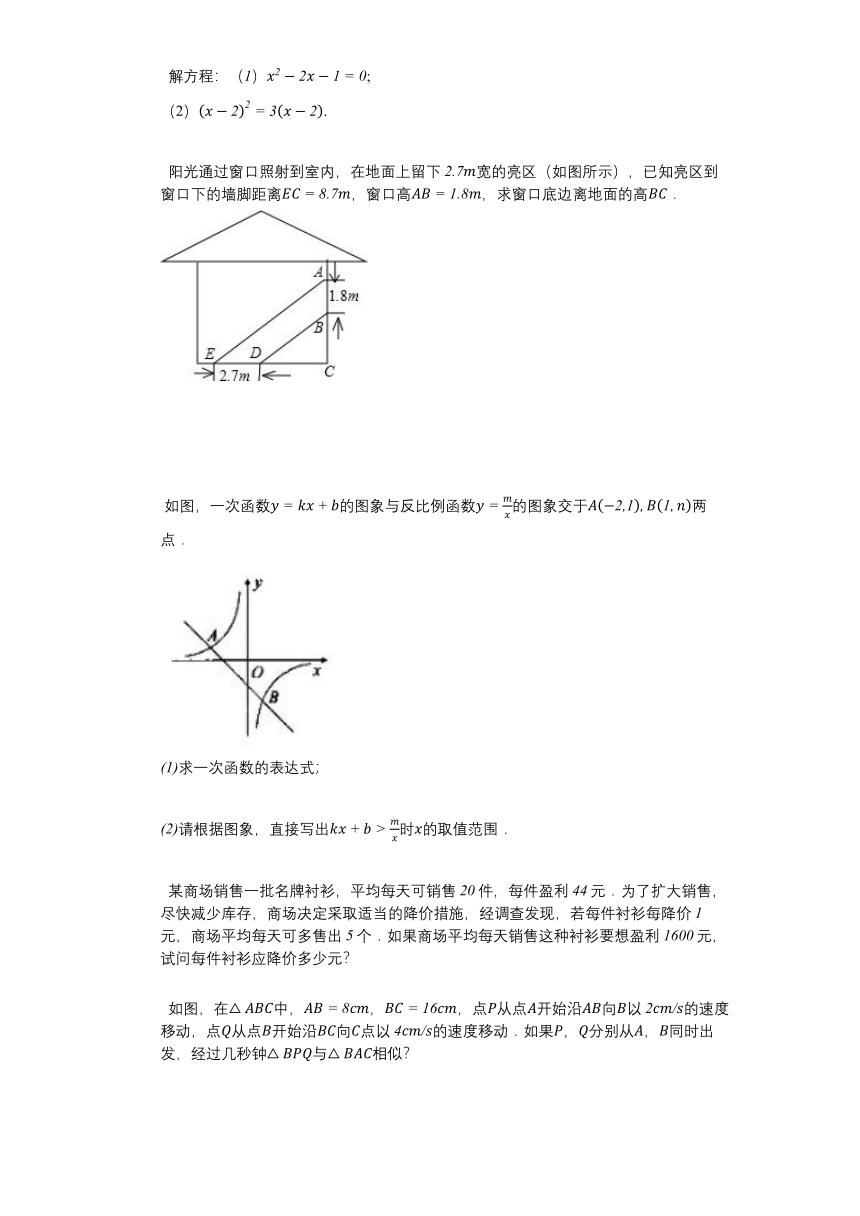
三、解答题
解方程:();
(2).
阳光通过窗口照射到室内,在地面上留下宽的亮区(如图所示),已知亮区到窗口下的墙脚距离,窗口高,求窗口底边离地面的高.
如图,一次函数的图象与反比例函数的图象交于两点.
求一次函数的表达式;
请根据图象,直接写出时的取值范围.
某商场销售一批名牌衬衫,平均每天可销售件,每件盈利元.为了扩大销售,尽快减少库存,商场决定采取适当的降价措施,经调查发现,若每件衬衫每降价元,商场平均每天可多售出个.如果商场平均每天销售这种衬衫要想盈利元,试问每件衬衫应降价多少元?
如图,在中,,,点从点开始沿向以的速度移动,点从点开始沿向点以的速度移动.如果,分别从,同时出发,经过几秒钟与相似?
如图,直角坐标系中,点坐标为,且轴于点,过作轴交过点的双曲线于点,连接交 于点,交于点.
求双曲线的表达式;
求的值.
阅读下列材料:
已知实数、满足,且,求的值.
解:∵ ,∴ 每一项都除以得,
又∵ 且
∴ 、是方程的两实根 ,由根与系数关系得,
∴ .
根据材料中所提供的方法,解答下列问题:
已知实数、满足,求的值;
已知实数、满足且,求的值.
如图,正方形的边长为,动点在边上从点沿向运动,以为边,在上方作正方形,连接.
求证:;
若设,当取何值时,最大?并求出的最大值.
连接,试探究:当点运动到边的什么位置时,?并说明理由.
参考答案与试题解析
2021-2022学年湖南省永州市初三(上)期中考试数学试卷
一、选择题
1.
【答案】
D
【考点】
一元二次方程的定义
【解析】
此题暂无解析
【解答】
D
2.
【答案】
D
【考点】
反比例函数的性质
【解析】
此题暂无解析
【解答】
D
3.
【答案】
C
【考点】
根与系数的关系
【解析】
此题暂无解析
【解答】
C
4.
【答案】
C
【考点】
相似三角形的性质与判定
平行四边形的性质
【解析】
由得,根据,可证,已知,利用相似比可求,由平行四边形的性质求解.
【解答】
解:∵ ,
∴ ,
又∵ ,
∴ ,
∴ ,
即,
解得,
由平行四边形的性质,
得.
故选.
5.
【答案】
A
【考点】
反比例函数的性质
一次函数的性质
【解析】
根据反比例函数的图象与系数的关系,当时,反比例函数的图象在第一、三象限;当时,反比例函数的图象在第二、四象限;根据一次函数的图像与系数的关系,当,一次函数的图象经过第一、二、三象限,当 ,时,一次函数的图象经过第、一、二、四象限,即可——判断得出答案.
【解答】
解:当时,反比例函数的图象在第一、三象限,
一次函数的图象经过第一、二、三象限,
可知项符合;,不符合题意;
当时,反比例函数的图象在第二、四象限,
一次函数的图象经过第一、二、四象限,则不符合题意.
故选.
6.
【答案】
C
【考点】
相似三角形的性质
【解析】
此题暂无解析
【解答】
C
7.
【答案】
B
【考点】
一元二次方程的应用——增长率问题
【解析】
此题暂无解析
【解答】
B
8.
【答案】
B
【考点】
相似三角形的判定
【解析】
根据已知及相似三角形的判定方法对各个选项进行分析,从而得到最后答案.
【解答】
解:∵ ,
∴ ,
∴ 当,时,,
故,选项不符合题意;
当时,可以判定三角形相似,
当时,不能判定三角形相似,
故选项不符合题意,选项符合题意.
故选.
9.
【答案】
C
【考点】
反比例函数图象上点的坐标特征
三角形的面积
【解析】
此题暂无解析
【解答】
C
10.
【答案】
B
【考点】
相似三角形的判定
矩形的性质
【解析】
此题暂无解析
【解答】
B
11.
【答案】
>
【考点】
反比例函数的性质
反比例函数图象上点的坐标特征
【解析】
此题暂无解析
【解答】
>
二、填空题
【答案】
【考点】
比例的性质
【解析】
此题暂无解析
【解答】
【答案】
16
【考点】
相似三角形的应用
【解析】
此题暂无解析
【解答】
16
【答案】
-2
【考点】
一元二次方程的定义
【解析】
此题暂无解析
【解答】
-2
【答案】
12
【考点】
相似三角形的应用
【解析】
此题暂无解析
【解答】
12
【答案】
-10
【考点】
反比例函数系数k的几何意义
【解析】
此题暂无解析
【解答】
-10
【答案】
且
【考点】
一元二次方程的定义
根的判别式
【解析】
此题暂无解析
【解答】
且
【答案】
1:3
【考点】
相似三角形的性质与判定
三角形的面积
【解析】
此题暂无解析
【解答】
1:3
三、解答题
【答案】
(1) , ;
(2) ,.
【考点】
解一元二次方程-因式分解法
解一元二次方程-配方法
【解析】
此题暂无解析
【解答】
(1) , ;
(2) ,.
【答案】
解:∵ ,
∴ ,
∴ .
∵ ,,
∴ .
∵ ,
∴ ,
∴ ,
∴ ,即窗口底边离地面的高为.
【考点】
相似三角形的应用
【解析】
因为光线、是一组平行光线,即,所以,则有,从而算出的长.
【解答】
解:∵ ,
∴ ,
∴ .
∵ ,,
∴ .
∵ ,
∴ ,
∴ ,
∴ ,即窗口底边离地面的高为.
【答案】
解:点,
,
.
在中,当时,,
点,
解得:
.
由图可得或.
【考点】
待定系数法求一次函数解析式
反比例函数与一次函数的综合
【解析】
左侧图片未给出解析
左侧图片未给出解析
【解答】
解:点,
,
.
在中,当时,,
点,
解得:
.
由图可得或.
【答案】
解:设每件衬衫应降价元,则销售量为件,每件利润为元,
依题意,得,
整理,得,
解得或(为了减少库存,不符合题意舍去).
故每件衬衫应降价元.
【考点】
一元二次方程的应用——利润问题
【解析】
设每件衬衫应降价元,根据平均每天可售出件,每件盈利元,为了扩大销售,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫降价元,商场每天可多售件.若商场平均每天要盈利元,可列方程求解.
【解答】
解:设每件衬衫应降价元,则销售量为件,每件利润为元,
依题意,得,
整理,得,
解得或(为了减少库存,不符合题意舍去).
故每件衬衫应降价元.
【答案】
解:设在开始运动后第秒,与相似,
由题意得:,,,
分两种情况考虑:
①当,时,,
∴ ,
即,
解得:,
则当秒时,与相似;
②当,时,,
∴ ,
即,
解得:,
则当秒时,与相似.
综上,当秒或秒时,与相似.
【考点】
相似三角形的性质
【解析】
设在开始运动后第秒,与相似,由题意表示出,,,分两种情况考虑:当,时,;当,时,,分别由相似得比例,列出关于的方程,求出方程的解得到的值,即可得到结果.
【解答】
解:设在开始运动后第秒,与相似,
由题意得:,,,
分两种情况考虑:
①当,时,,
∴ ,
即,
解得:,
则当秒时,与相似;
②当,时,,
∴ ,
即,
解得:,
则当秒时,与相似.
综上,当秒或秒时,与相似.
【答案】
(1)A(,),双曲线表达式.
(2) , .
【考点】
待定系数法求反比例函数解析式
相似三角形的性质与判定
【解析】
此题暂无解析
【解答】
(1)A(,),双曲线表达式.
(2) , .
【答案】
(1) ,
∴ 、是方程的根,
第种情形,时,由根与系数关系得,
∴ ;
第种情形,时, ,故值为或
(2)∵ , ∴ 每一项都除以得,
又,且,
∴ 、是方程的两实根,
由根与系数关系得,
∴ .
【考点】
根与系数的关系
一元二次方程的解
【解析】
此题暂无解析
【解答】
(1) ,
∴ 、是方程的根,
第种情形,时,由根与系数关系得,
∴ ;
第种情形,时, ,故值为或
(2)∵ , ∴ 每一项都除以得,
又,且,
∴ 、是方程的两实根,
由根与系数关系得,
∴ .
【答案】
解:∵ , , .
.
∴ .
∴ .
∴
当时,有最大值为.
当点是的中点时,,
理由:∵ 是中点,
∴ .
∴ .
又∵ ,
∴ .
又∵ ,
∴ .
又,
∴ .
【考点】
相似三角形的判定
正方形的性质
相似三角形的性质
相似三角形的性质与判定
【解析】
(1)=,要证结论,必证,由正方形的性质很快确定=,又=,=,符合即证.
(2)先证,所以,即可求出函数解析式=,继而求出最值.
(3)要使,需,又因为,所以,即,所以当点是的中点时,.
【解答】
解:∵ , , .
.
∴ .
∴ .
∴
当时,有最大值为.
当点是的中点时,,
理由:∵ 是中点,
∴ .
∴ .
又∵ ,
∴ .
又∵ ,
∴ .
又,
∴ .
一、选择题
1. 下列方程是一元二次方程的是( )
A. B. C. D.
2. 关于反比例函数,下列说法不正确的是( )
A.图象经过 B.图象位于一、三象限
C.图象关于直线对称 D.随的增大而增大
3. 已知是方程的两根,则的值为( )
A. B. C. D.
4. 如图,在 中,,,,则的长为( )
A. B. C. D.
5. 在同一坐标系中,函数和的图象大致是( )
A. B. C. D.
6. 已知与是位似三角形,且,则与的周长之比为( )
A. B. C. D.
7. 永州市年底城市绿地面积是万平方米,计划到年底城市绿地面积提高到万平方米,则平均每年的增长率为( )
A. B. C. D.
8. 如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B.
C. D.
9. 如图,直线与反比例函数的图象分别交于、两点,若点是轴上任意一点,则的面积是( )
A. B. C. D.不确定
10. 如图,矩形中,,在边上取一点,使得与相似,则这样的点共有( )
A.个 B.个 C.个 D.个
11. 若点都在双曲线上,则大小关系为________.
二、填空题
若,则________.
如图,小孔成像示意图:根据图中标注的尺寸,如果物体的高度为,那么它在暗盒中所成的像的高度为________.
若关于的方程为一元二次方程,则________.
现测得身高为米的甲同学的影长为米,那么同一时刻影长为米的乙旗杆的高度是________米.
如图,为反比例函数图象上一点,轴于,且,则________.
若关于的一元二次方程有两个不相等实数根,则的范围是________.
如图,四边形中,,、交于点,,则________.
三、解答题
解方程:();
(2).
阳光通过窗口照射到室内,在地面上留下宽的亮区(如图所示),已知亮区到窗口下的墙脚距离,窗口高,求窗口底边离地面的高.
如图,一次函数的图象与反比例函数的图象交于两点.
求一次函数的表达式;
请根据图象,直接写出时的取值范围.
某商场销售一批名牌衬衫,平均每天可销售件,每件盈利元.为了扩大销售,尽快减少库存,商场决定采取适当的降价措施,经调查发现,若每件衬衫每降价元,商场平均每天可多售出个.如果商场平均每天销售这种衬衫要想盈利元,试问每件衬衫应降价多少元?
如图,在中,,,点从点开始沿向以的速度移动,点从点开始沿向点以的速度移动.如果,分别从,同时出发,经过几秒钟与相似?
如图,直角坐标系中,点坐标为,且轴于点,过作轴交过点的双曲线于点,连接交 于点,交于点.
求双曲线的表达式;
求的值.
阅读下列材料:
已知实数、满足,且,求的值.
解:∵ ,∴ 每一项都除以得,
又∵ 且
∴ 、是方程的两实根 ,由根与系数关系得,
∴ .
根据材料中所提供的方法,解答下列问题:
已知实数、满足,求的值;
已知实数、满足且,求的值.
如图,正方形的边长为,动点在边上从点沿向运动,以为边,在上方作正方形,连接.
求证:;
若设,当取何值时,最大?并求出的最大值.
连接,试探究:当点运动到边的什么位置时,?并说明理由.
参考答案与试题解析
2021-2022学年湖南省永州市初三(上)期中考试数学试卷
一、选择题
1.
【答案】
D
【考点】
一元二次方程的定义
【解析】
此题暂无解析
【解答】
D
2.
【答案】
D
【考点】
反比例函数的性质
【解析】
此题暂无解析
【解答】
D
3.
【答案】
C
【考点】
根与系数的关系
【解析】
此题暂无解析
【解答】
C
4.
【答案】
C
【考点】
相似三角形的性质与判定
平行四边形的性质
【解析】
由得,根据,可证,已知,利用相似比可求,由平行四边形的性质求解.
【解答】
解:∵ ,
∴ ,
又∵ ,
∴ ,
∴ ,
即,
解得,
由平行四边形的性质,
得.
故选.
5.
【答案】
A
【考点】
反比例函数的性质
一次函数的性质
【解析】
根据反比例函数的图象与系数的关系,当时,反比例函数的图象在第一、三象限;当时,反比例函数的图象在第二、四象限;根据一次函数的图像与系数的关系,当,一次函数的图象经过第一、二、三象限,当 ,时,一次函数的图象经过第、一、二、四象限,即可——判断得出答案.
【解答】
解:当时,反比例函数的图象在第一、三象限,
一次函数的图象经过第一、二、三象限,
可知项符合;,不符合题意;
当时,反比例函数的图象在第二、四象限,
一次函数的图象经过第一、二、四象限,则不符合题意.
故选.
6.
【答案】
C
【考点】
相似三角形的性质
【解析】
此题暂无解析
【解答】
C
7.
【答案】
B
【考点】
一元二次方程的应用——增长率问题
【解析】
此题暂无解析
【解答】
B
8.
【答案】
B
【考点】
相似三角形的判定
【解析】
根据已知及相似三角形的判定方法对各个选项进行分析,从而得到最后答案.
【解答】
解:∵ ,
∴ ,
∴ 当,时,,
故,选项不符合题意;
当时,可以判定三角形相似,
当时,不能判定三角形相似,
故选项不符合题意,选项符合题意.
故选.
9.
【答案】
C
【考点】
反比例函数图象上点的坐标特征
三角形的面积
【解析】
此题暂无解析
【解答】
C
10.
【答案】
B
【考点】
相似三角形的判定
矩形的性质
【解析】
此题暂无解析
【解答】
B
11.
【答案】
>
【考点】
反比例函数的性质
反比例函数图象上点的坐标特征
【解析】
此题暂无解析
【解答】
>
二、填空题
【答案】
【考点】
比例的性质
【解析】
此题暂无解析
【解答】
【答案】
16
【考点】
相似三角形的应用
【解析】
此题暂无解析
【解答】
16
【答案】
-2
【考点】
一元二次方程的定义
【解析】
此题暂无解析
【解答】
-2
【答案】
12
【考点】
相似三角形的应用
【解析】
此题暂无解析
【解答】
12
【答案】
-10
【考点】
反比例函数系数k的几何意义
【解析】
此题暂无解析
【解答】
-10
【答案】
且
【考点】
一元二次方程的定义
根的判别式
【解析】
此题暂无解析
【解答】
且
【答案】
1:3
【考点】
相似三角形的性质与判定
三角形的面积
【解析】
此题暂无解析
【解答】
1:3
三、解答题
【答案】
(1) , ;
(2) ,.
【考点】
解一元二次方程-因式分解法
解一元二次方程-配方法
【解析】
此题暂无解析
【解答】
(1) , ;
(2) ,.
【答案】
解:∵ ,
∴ ,
∴ .
∵ ,,
∴ .
∵ ,
∴ ,
∴ ,
∴ ,即窗口底边离地面的高为.
【考点】
相似三角形的应用
【解析】
因为光线、是一组平行光线,即,所以,则有,从而算出的长.
【解答】
解:∵ ,
∴ ,
∴ .
∵ ,,
∴ .
∵ ,
∴ ,
∴ ,
∴ ,即窗口底边离地面的高为.
【答案】
解:点,
,
.
在中,当时,,
点,
解得:
.
由图可得或.
【考点】
待定系数法求一次函数解析式
反比例函数与一次函数的综合
【解析】
左侧图片未给出解析
左侧图片未给出解析
【解答】
解:点,
,
.
在中,当时,,
点,
解得:
.
由图可得或.
【答案】
解:设每件衬衫应降价元,则销售量为件,每件利润为元,
依题意,得,
整理,得,
解得或(为了减少库存,不符合题意舍去).
故每件衬衫应降价元.
【考点】
一元二次方程的应用——利润问题
【解析】
设每件衬衫应降价元,根据平均每天可售出件,每件盈利元,为了扩大销售,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫降价元,商场每天可多售件.若商场平均每天要盈利元,可列方程求解.
【解答】
解:设每件衬衫应降价元,则销售量为件,每件利润为元,
依题意,得,
整理,得,
解得或(为了减少库存,不符合题意舍去).
故每件衬衫应降价元.
【答案】
解:设在开始运动后第秒,与相似,
由题意得:,,,
分两种情况考虑:
①当,时,,
∴ ,
即,
解得:,
则当秒时,与相似;
②当,时,,
∴ ,
即,
解得:,
则当秒时,与相似.
综上,当秒或秒时,与相似.
【考点】
相似三角形的性质
【解析】
设在开始运动后第秒,与相似,由题意表示出,,,分两种情况考虑:当,时,;当,时,,分别由相似得比例,列出关于的方程,求出方程的解得到的值,即可得到结果.
【解答】
解:设在开始运动后第秒,与相似,
由题意得:,,,
分两种情况考虑:
①当,时,,
∴ ,
即,
解得:,
则当秒时,与相似;
②当,时,,
∴ ,
即,
解得:,
则当秒时,与相似.
综上,当秒或秒时,与相似.
【答案】
(1)A(,),双曲线表达式.
(2) , .
【考点】
待定系数法求反比例函数解析式
相似三角形的性质与判定
【解析】
此题暂无解析
【解答】
(1)A(,),双曲线表达式.
(2) , .
【答案】
(1) ,
∴ 、是方程的根,
第种情形,时,由根与系数关系得,
∴ ;
第种情形,时, ,故值为或
(2)∵ , ∴ 每一项都除以得,
又,且,
∴ 、是方程的两实根,
由根与系数关系得,
∴ .
【考点】
根与系数的关系
一元二次方程的解
【解析】
此题暂无解析
【解答】
(1) ,
∴ 、是方程的根,
第种情形,时,由根与系数关系得,
∴ ;
第种情形,时, ,故值为或
(2)∵ , ∴ 每一项都除以得,
又,且,
∴ 、是方程的两实根,
由根与系数关系得,
∴ .
【答案】
解:∵ , , .
.
∴ .
∴ .
∴
当时,有最大值为.
当点是的中点时,,
理由:∵ 是中点,
∴ .
∴ .
又∵ ,
∴ .
又∵ ,
∴ .
又,
∴ .
【考点】
相似三角形的判定
正方形的性质
相似三角形的性质
相似三角形的性质与判定
【解析】
(1)=,要证结论,必证,由正方形的性质很快确定=,又=,=,符合即证.
(2)先证,所以,即可求出函数解析式=,继而求出最值.
(3)要使,需,又因为,所以,即,所以当点是的中点时,.
【解答】
解:∵ , , .
.
∴ .
∴ .
∴
当时,有最大值为.
当点是的中点时,,
理由:∵ 是中点,
∴ .
∴ .
又∵ ,
∴ .
又∵ ,
∴ .
又,
∴ .
同课章节目录
