2021-2022学年北师大版八年级数学上册1.1.1 勾股定理的定义及简单应用 同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册1.1.1 勾股定理的定义及简单应用 同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 186.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 08:44:14 | ||
图片预览


文档简介
1.1.1 勾股定理的定义及简单应用同步练习 2021-2022学年北师大版八年级数学上册
题号 一 二 三 总分
得分
一、选择题(本大题共5小题,共15分)
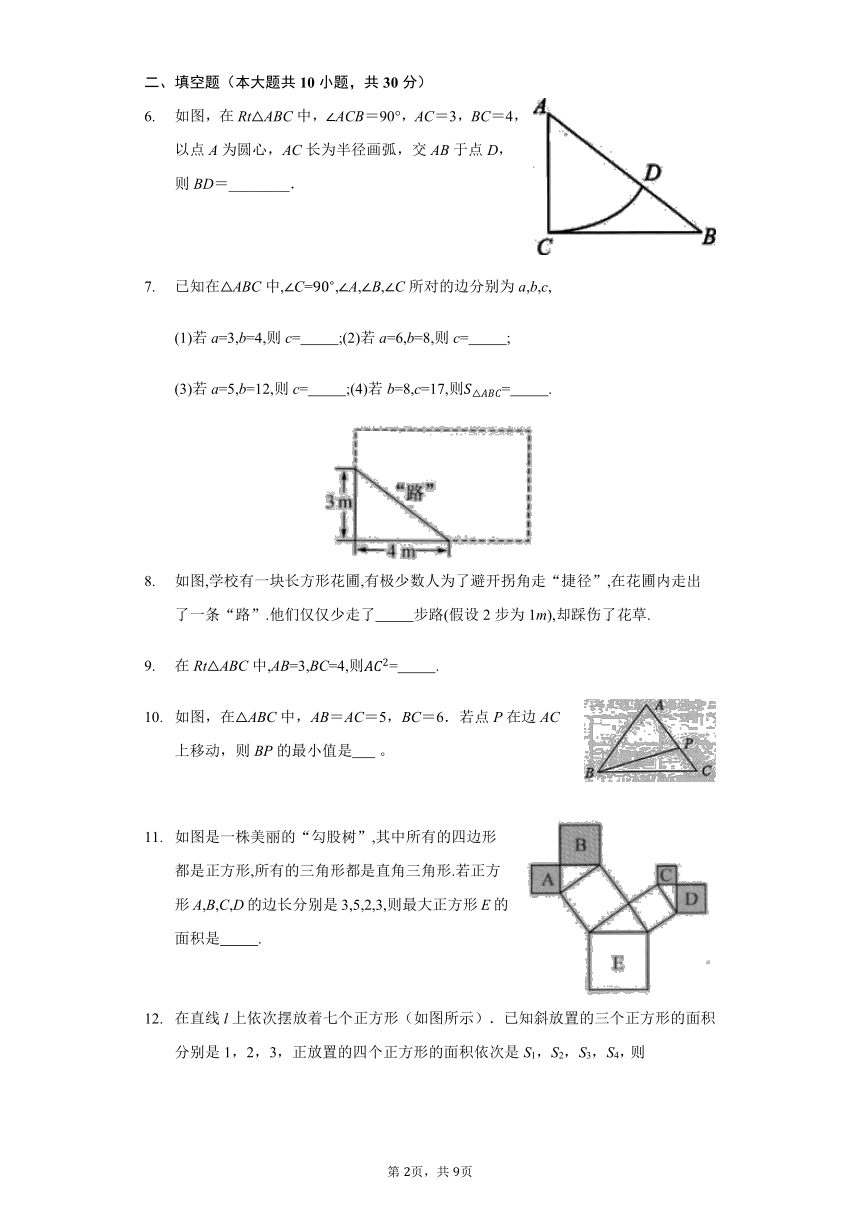
下列说法正确的是( )
A. 若,,是的三边,则
B. 若,,是的三边,则
C. 若,,是的三边,,则
D. 若,,是的三边,,则
如图所示,正方形的数字表示该正方形的面积,则字母B所表示的正方形面积是 ( )
A. B. C. D.
如图所示,已知RtABC中,AB=4,分别以AC, BC为直径作半圆,面积分别记为,,则+的值等于( )
A. B. C. D.
如图,一支铅笔放在圆柱形笔筒中,笔筒内部的底面直径BC为9 cm,内壁高为12 cm,则这支铅笔的长度可能是( )
A. B. C. D.
如图,在RtABC中,ACB=,BC=6,AC=8,则RtABC的斜边AB上的高CD的长是( )
A. B. C. D.
二、填空题(本大题共10小题,共30分)
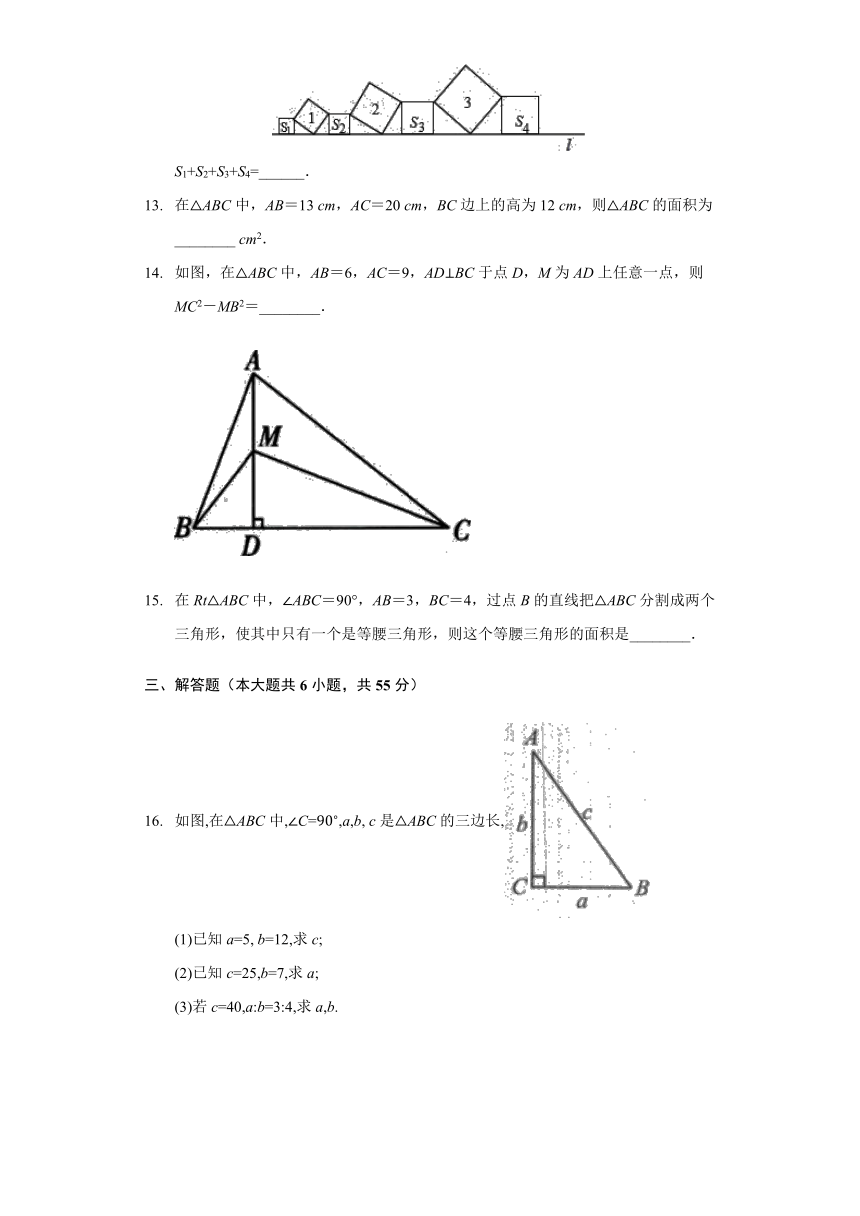
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点A为圆心,AC长为半径画弧,交AB于点D,则BD=________.
已知在ABC中,C=,A,B,C所对的边分别为a,b,c,
(1)若a=3,b=4,则c= ;(2)若a=6,b=8,则c= ;
(3)若a=5,b=12,则c= ;(4)若b=8,c=17,则= .
如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 步路(假设2步为1m),却踩伤了花草.
在RtABC中,AB=3,BC=4,则= .
如图,在△ABC中,AB=AC=5,BC=6.若点P在边AC上移动,则BP的最小值是 。
如图是一株美丽的“勾股树”,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是3,5,2,3,则最大正方形E的面积是 .
在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4=______.
在△ABC中,AB=13 cm,AC=20 cm,BC边上的高为12 cm,则△ABC的面积为________ cm2.
如图,在△ABC中,AB=6,AC=9,AD⊥BC于点D,M为AD上任意一点,则MC2-MB2=________.
在Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是________.
三、解答题(本大题共6小题,共55分)
如图,在ABC中,C=,a,b, c是ABC的三边长,
(1)已知a=5, b=12,求c;
(2)已知c=25,b=7,求a;
(3)若c=40,a:b=3:4,求a,b.
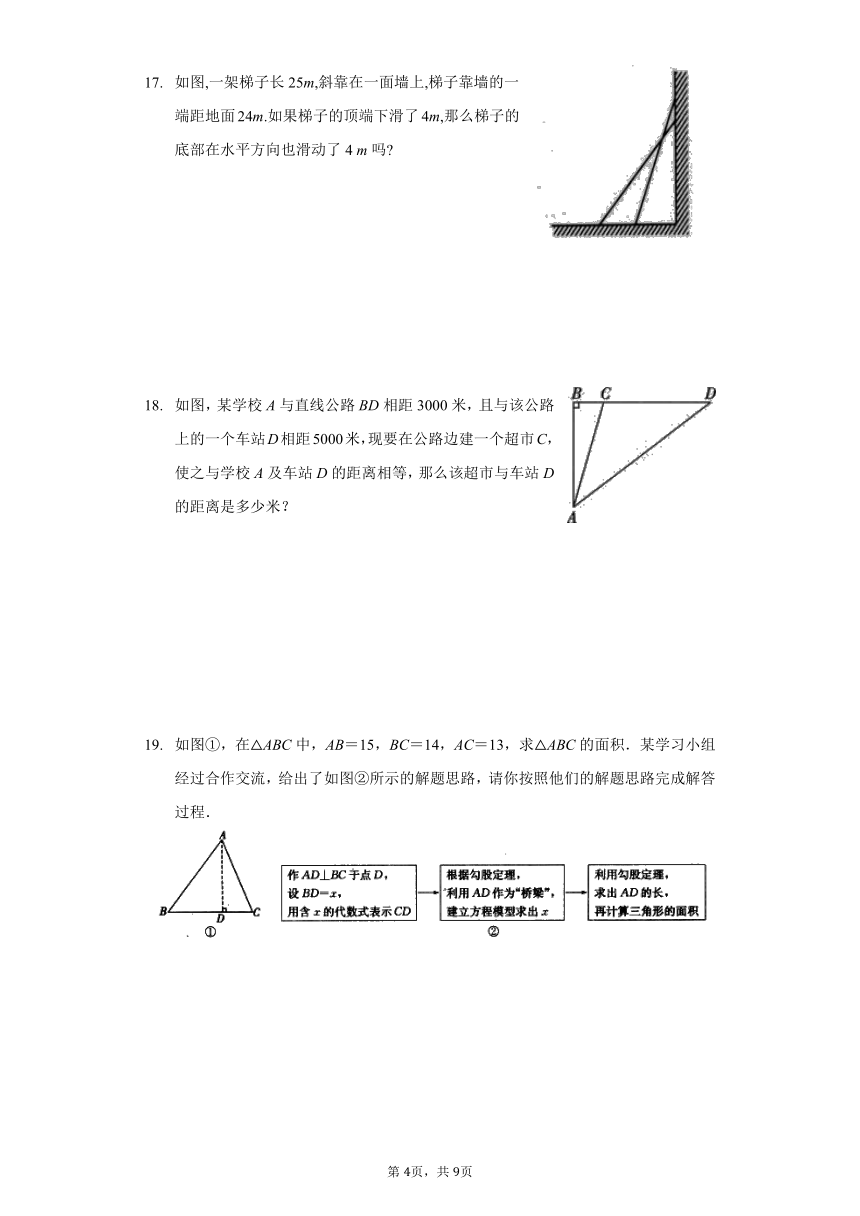
如图,一架梯子长25m,斜靠在一面墙上,梯子靠墙的一端距地面24m.如果梯子的顶端下滑了4m,那么梯子的底部在水平方向也滑动了4 m吗
如图,某学校A与直线公路BD相距3000米,且与该公路上的一个车站D相距5000米,现要在公路边建一个超市C,使之与学校A及车站D的距离相等,那么该超市与车站D的距离是多少米?
如图①,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了如图②所示的解题思路,请你按照他们的解题思路完成解答过程.
如图,一个牧童在距离小河岸南400米的A处牧马,而他的家位于牧马处A的东800米(BC=800米),南700米(AC=700米)处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?
如图,ACB和ECD都是等腰直角三角形,ACB=ECD=,D为AB边上一点.求证:
(1)ACEBCD;
(2)=+.
参考答案
1.【答案】D
2.【答案】C
3.【答案】A
4.【答案】D
5.【答案】B
6.【答案】2
7.【答案】(1)5;
(2)10;
(3)13;
(4)60
8.【答案】4
9.【答案】7或25
10.【答案】4.8
11.【答案】47
12.【答案】4
13.【答案】126或66
14.【答案】45
15.【答案】3.6或4.32或4.8
16.【答案】解:(1)=+=+=169,
所以c=13;
(2)=-=-=576,
所以a=24;
(3)设a=3x,b=4x,
则+=,
解得x=8,
所以a=24,b=32.
17.【答案】解:如图
由题意知AB==25(米),AO=24(米),
∵在直角△ABO中,
∴BO=7(米),
∵=4(米),
∴O=24=20(米),
∵在直角△中,
∴=15(米),
==8(米),
∴梯子的底部在水平方向上滑动为8米,
故如果梯子的顶端下滑了4m,那么梯子的底部在水平方向不是滑动了4m.
18.【答案】解:根据题意得:AC=CD,∠ABD=90°.
在直角三角形ABD中,
∵AB=3000米,AD=5000米,
∴BD=4000(米),
设CD=AC=x米,BC=4000-x(米),
在Rt△ABC中,AC2=AB2+BC2,
即x2=30002+(4000-x)2
解得:x=3125,
答:该超市与车站D的距离是3125米.
19.【答案】解:如图,作AD⊥BC于点D,
在△ABC中,AB=15,BC=14,AC=13,
设BD=x,则CD=14-x,
由勾股定理得:AD2=AB2-BD2=152-x2,AD2=AC2-CD2=132-(14-x)2,
故152-x2=132-(14-x)2,
解之得x=9.
∴AD=12.
∴S△ABC=BC AD=×14×12=84.
20.【答案】解:如图,作A点关于小河南岸的对称点A′,连接BA′交河岸于点P,
则PB+PA=PB+PA′=BA′最短.
在△A′BC中,∠C=90°,BC=800米,A′C=AA′+AC=400×2+700=1500(米),
由勾股定理得A′B2=BC2+A′C2=17002.
∴A′B=1700米.
故他要完成这件事情所走的最短路程是1700米.
21.【答案】解:(1)ACB和ECD都是等腰直角三角形,
AC=BC,CD=CE.
ACB=ECD=,
BCD+ACD=ACE+ACD.
BCD=ACE.
在ACE和BCD中,
ACEBCD(SAS).
(2)ACB是等腰直角三角形,
B= BAC=.
ACEBCD,
AE=BD,CAE=B=.
DAE=CAE+BAC=+=.
+=.
+=.
又ECD是等腰直角三角形,
+==.
=+.
第4页,共9页
题号 一 二 三 总分
得分
一、选择题(本大题共5小题,共15分)
下列说法正确的是( )
A. 若,,是的三边,则
B. 若,,是的三边,则
C. 若,,是的三边,,则
D. 若,,是的三边,,则
如图所示,正方形的数字表示该正方形的面积,则字母B所表示的正方形面积是 ( )
A. B. C. D.
如图所示,已知RtABC中,AB=4,分别以AC, BC为直径作半圆,面积分别记为,,则+的值等于( )
A. B. C. D.
如图,一支铅笔放在圆柱形笔筒中,笔筒内部的底面直径BC为9 cm,内壁高为12 cm,则这支铅笔的长度可能是( )
A. B. C. D.
如图,在RtABC中,ACB=,BC=6,AC=8,则RtABC的斜边AB上的高CD的长是( )
A. B. C. D.
二、填空题(本大题共10小题,共30分)
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点A为圆心,AC长为半径画弧,交AB于点D,则BD=________.
已知在ABC中,C=,A,B,C所对的边分别为a,b,c,
(1)若a=3,b=4,则c= ;(2)若a=6,b=8,则c= ;
(3)若a=5,b=12,则c= ;(4)若b=8,c=17,则= .
如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 步路(假设2步为1m),却踩伤了花草.
在RtABC中,AB=3,BC=4,则= .
如图,在△ABC中,AB=AC=5,BC=6.若点P在边AC上移动,则BP的最小值是 。
如图是一株美丽的“勾股树”,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是3,5,2,3,则最大正方形E的面积是 .
在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4=______.
在△ABC中,AB=13 cm,AC=20 cm,BC边上的高为12 cm,则△ABC的面积为________ cm2.
如图,在△ABC中,AB=6,AC=9,AD⊥BC于点D,M为AD上任意一点,则MC2-MB2=________.
在Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是________.
三、解答题(本大题共6小题,共55分)
如图,在ABC中,C=,a,b, c是ABC的三边长,
(1)已知a=5, b=12,求c;
(2)已知c=25,b=7,求a;
(3)若c=40,a:b=3:4,求a,b.
如图,一架梯子长25m,斜靠在一面墙上,梯子靠墙的一端距地面24m.如果梯子的顶端下滑了4m,那么梯子的底部在水平方向也滑动了4 m吗
如图,某学校A与直线公路BD相距3000米,且与该公路上的一个车站D相距5000米,现要在公路边建一个超市C,使之与学校A及车站D的距离相等,那么该超市与车站D的距离是多少米?
如图①,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了如图②所示的解题思路,请你按照他们的解题思路完成解答过程.
如图,一个牧童在距离小河岸南400米的A处牧马,而他的家位于牧马处A的东800米(BC=800米),南700米(AC=700米)处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?
如图,ACB和ECD都是等腰直角三角形,ACB=ECD=,D为AB边上一点.求证:
(1)ACEBCD;
(2)=+.
参考答案
1.【答案】D
2.【答案】C
3.【答案】A
4.【答案】D
5.【答案】B
6.【答案】2
7.【答案】(1)5;
(2)10;
(3)13;
(4)60
8.【答案】4
9.【答案】7或25
10.【答案】4.8
11.【答案】47
12.【答案】4
13.【答案】126或66
14.【答案】45
15.【答案】3.6或4.32或4.8
16.【答案】解:(1)=+=+=169,
所以c=13;
(2)=-=-=576,
所以a=24;
(3)设a=3x,b=4x,
则+=,
解得x=8,
所以a=24,b=32.
17.【答案】解:如图
由题意知AB==25(米),AO=24(米),
∵在直角△ABO中,
∴BO=7(米),
∵=4(米),
∴O=24=20(米),
∵在直角△中,
∴=15(米),
==8(米),
∴梯子的底部在水平方向上滑动为8米,
故如果梯子的顶端下滑了4m,那么梯子的底部在水平方向不是滑动了4m.
18.【答案】解:根据题意得:AC=CD,∠ABD=90°.
在直角三角形ABD中,
∵AB=3000米,AD=5000米,
∴BD=4000(米),
设CD=AC=x米,BC=4000-x(米),
在Rt△ABC中,AC2=AB2+BC2,
即x2=30002+(4000-x)2
解得:x=3125,
答:该超市与车站D的距离是3125米.
19.【答案】解:如图,作AD⊥BC于点D,
在△ABC中,AB=15,BC=14,AC=13,
设BD=x,则CD=14-x,
由勾股定理得:AD2=AB2-BD2=152-x2,AD2=AC2-CD2=132-(14-x)2,
故152-x2=132-(14-x)2,
解之得x=9.
∴AD=12.
∴S△ABC=BC AD=×14×12=84.
20.【答案】解:如图,作A点关于小河南岸的对称点A′,连接BA′交河岸于点P,
则PB+PA=PB+PA′=BA′最短.
在△A′BC中,∠C=90°,BC=800米,A′C=AA′+AC=400×2+700=1500(米),
由勾股定理得A′B2=BC2+A′C2=17002.
∴A′B=1700米.
故他要完成这件事情所走的最短路程是1700米.
21.【答案】解:(1)ACB和ECD都是等腰直角三角形,
AC=BC,CD=CE.
ACB=ECD=,
BCD+ACD=ACE+ACD.
BCD=ACE.
在ACE和BCD中,
ACEBCD(SAS).
(2)ACB是等腰直角三角形,
B= BAC=.
ACEBCD,
AE=BD,CAE=B=.
DAE=CAE+BAC=+=.
+=.
+=.
又ECD是等腰直角三角形,
+==.
=+.
第4页,共9页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
