2021-2022学年北师大版九年级数学下册1.6利用三角函数测高 优生辅导训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册1.6利用三角函数测高 优生辅导训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 419.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 08:45:32 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《1.6利用三角函数测高》优生辅导训练(附答案)
1.一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以80海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上,求此时货轮距灯塔A的距离AB(结果保留3个有效数字,≈2.449).
2.如图,某渔船向正东方向以12海里时的速度航行,在A处测得岛C在北偏东的60°方向,1小时后渔船航行到B处,测得岛C在北偏东的30°方向,已知该岛周围10海里内有暗礁.
(1)B处离岛C有多远?
(2)如果渔船继续向东航行,需要多长时间到达距离岛C最近的位置?
(3)如果渔船继续向东航行,有无触礁危险?
3.一艘轮船由南向北航行,如图,在A处测得小岛P在北偏西15°方向上,两个小时后,轮船在B处测得小岛P在北偏西30°方向上,在小岛周围18海里内有暗礁,问若轮船按20海里/时的速度继续向北航行,有无触礁的危险?
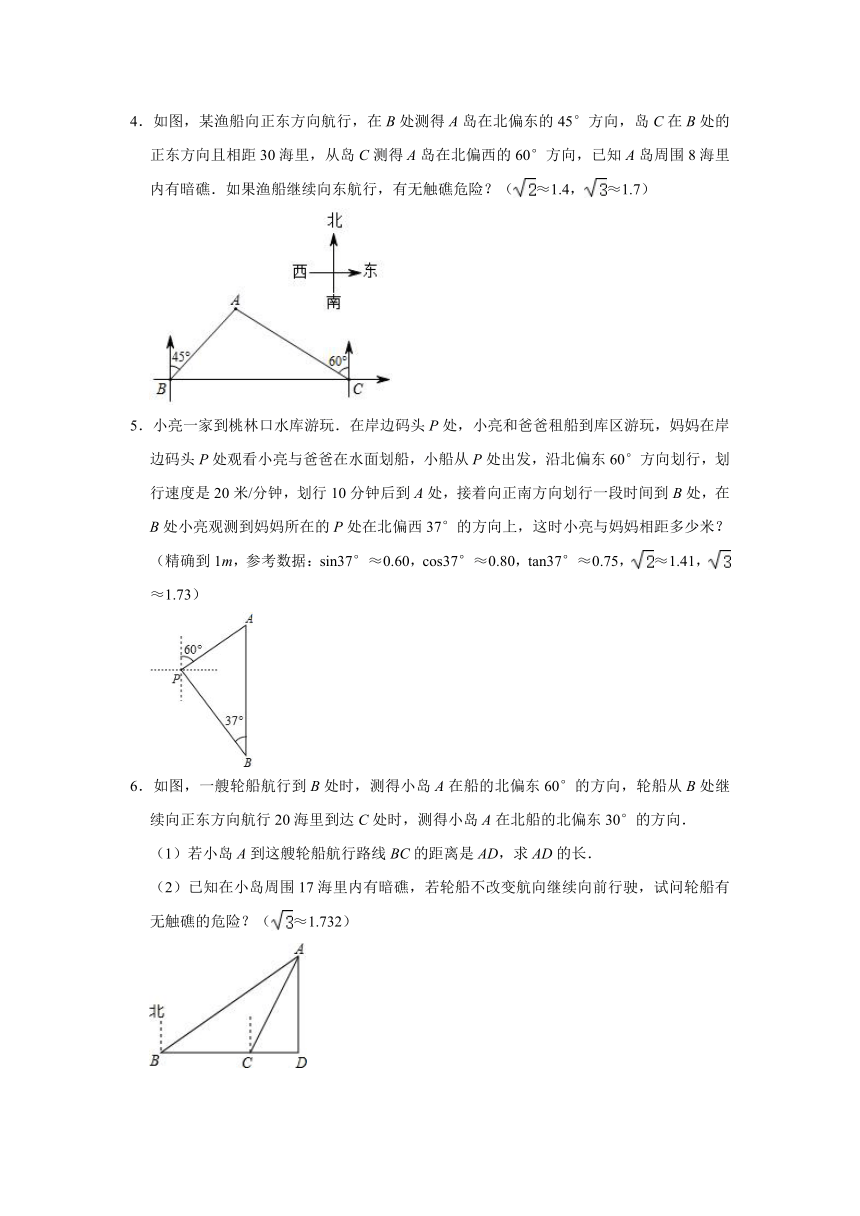
4.如图,某渔船向正东方向航行,在B处测得A岛在北偏东的45°方向,岛C在B处的正东方向且相距30海里,从岛C测得A岛在北偏西的60°方向,已知A岛周围8海里内有暗礁.如果渔船继续向东航行,有无触礁危险?(≈1.4,≈1.7)
5.小亮一家到桃林口水库游玩.在岸边码头P处,小亮和爸爸租船到库区游玩,妈妈在岸边码头P处观看小亮与爸爸在水面划船,小船从P处出发,沿北偏东60°方向划行,划行速度是20米/分钟,划行10分钟后到A处,接着向正南方向划行一段时间到B处,在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米?(精确到1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41,≈1.73)
6.如图,一艘轮船航行到B处时,测得小岛A在船的北偏东60°的方向,轮船从B处继续向正东方向航行20海里到达C处时,测得小岛A在北船的北偏东30°的方向.
(1)若小岛A到这艘轮船航行路线BC的距离是AD,求AD的长.
(2)已知在小岛周围17海里内有暗礁,若轮船不改变航向继续向前行驶,试问轮船有无触礁的危险?(≈1.732)
7.如图,某测量船位于海岛P的北偏西60°方向,距离海岛200海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的西南方向上的B处.求测量船从A处航行到B处的路程(结果保留根号).
8.如图,在东西方向的海岸线MN上有A,B两艘船,船长都收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向36海里处,船P在船B顶点北偏西37°方向,若船A,船B分别以30海里/小时,20海里/小时的速度同时出发,匀速前往救援,通过计算判断哪艘船先到达船P处.(参考数据=1.73,sin37°=0.6,cos37°=0.80)
9.4月12日上午,蓝鲸凌波,战舰驰骋,银鹰翱翔,中央军委在南海某海域举行海上阅兵,如图,军舰位于军舰P的北偏东60°方向上,两舰的距离为120海里,军舰B位于军舰A的正南方向,军舰P的南偏东45°方向上,求军舰B与军舰P之间的距离(结果保留根号).
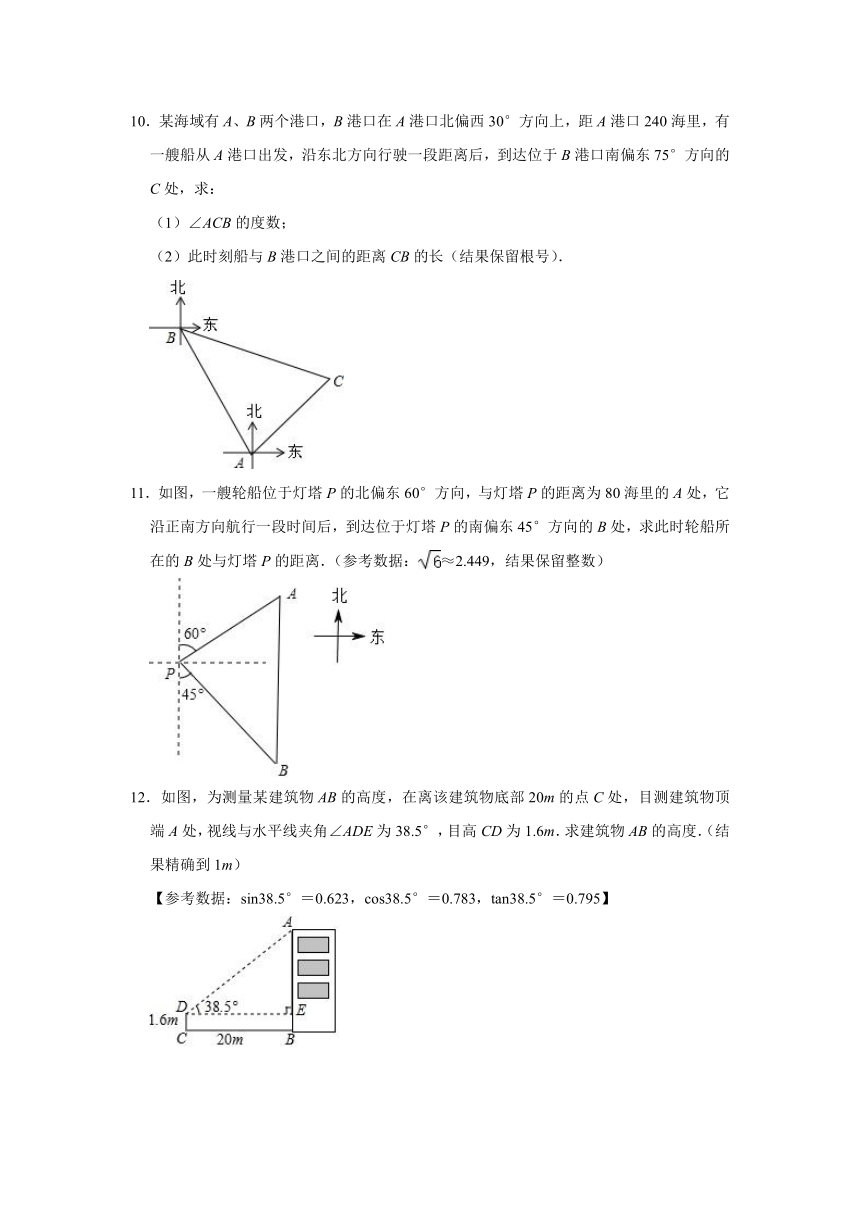
10.某海域有A、B两个港口,B港口在A港口北偏西30°方向上,距A港口240海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求:
(1)∠ACB的度数;
(2)此时刻船与B港口之间的距离CB的长(结果保留根号).
11.如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:≈2.449,结果保留整数)
12.如图,为测量某建筑物AB的高度,在离该建筑物底部20m的点C处,目测建筑物顶端A处,视线与水平线夹角∠ADE为38.5°,目高CD为1.6m.求建筑物AB的高度.(结果精确到1m)
【参考数据:sin38.5°=0.623,cos38.5°=0.783,tan38.5°=0.795】
13.如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了40m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(结果精确到1m)(参考数据:≈1.732,≈1.414)
14.敦煌莫高窟是甘肃省敦煌市境内的莫高窟、西千佛洞的总称,是我国著名的四大石窟之一,也是世界上现存规模最宏大、保存最完好的佛教艺术宝库,数学课外实践活动中,小明为测量莫高窟内佛像高度,分别在点D、H处用高为1.5米的测角仪对佛像进行了测量,如图,测得∠ACE=42°,∠AFE=61°,若DH=15米,求佛像的高度AB.(结果精确到1米,参考数据sin42°≈0.67,tan42°≈0.90,sin61°≈0.87,tan61°≈1.80)
15.如图,小山岗的斜坡AC的坡度是tanα=,在与山脚C水平距离300米的D处,测得山顶A的仰角为30°,点B、C、D在同一条直线上,求小山岗的高AB(结果保留整数或保留精确值)(参考数据≈1.732)
16.如图,某大楼的顶部竖有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:≈1.414,≈1.732)
17.某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端A处,测得仰角为45°,再往建筑物的方向前进6米到达D处,测得仰角为60°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米,≈1.732,≈1.414)
18.如图,线段AB、CD分别表示在同一水平线上的甲、乙两建筑物的高,AB⊥BD,CD⊥BD,垂足分别为B、D.从B点测到C点的仰角α为60°,从A点测得C点的仰角β为30°,甲建筑物的高AB=30米.
(1)求甲、乙两建筑物之间的距离BD.
(2)求乙建筑物的高CD.
19.如图,斜坡BE,坡顶B到水平地面的距离AB为3米,坡底AE为18米,在B处,E处分别测得CD顶部点D的仰角为30°,60°,求CD的高度.(结果保留根号)
20.热气球的探测器显示,从热气球底部a处看一栋高楼顶部的俯角为30°,看这栋楼底部俯角为60°,热气球a处与地面距离为420米,求这栋楼的高度.
21.某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进20m到达点D处,又测得点A的仰角为60°,则建筑物AB的高度是多少m?(结果用根式表示)
参考答案
1.解:由示意图可知:∠ACB=60°,
由平行线的性质可知∠ABC=180°﹣30°﹣75°=75°,
则∠A=180°﹣∠C﹣∠B=45°,BC=80×=40(海里),
过B作BD⊥AC于点D,
则∠BDC=90°,∠DBC=30°,
∴DC=BC=20海里,
由勾股定理得:BD=20海里,
∵∠A=45°,∠ADB=90°,
∴∠ABD=∠A=45°,
∴AD=BD=20海里,
由勾股定理得:AB===20≈49.0(海里),
答:此时货轮距灯塔A的距离AB为49.0海里.
2.解:(1)过C作CO⊥AB于O,则CO为渔船向东航行到C道最短距离,
∵在A处测得岛C在北偏东的60°,
∴∠CAB=30°,
又∵B处测得岛C在北偏东30°,
∴∠CBO=60°,∠ABC=120°,
∴∠ACB=∠CAB=30°,
∴AB=BC=12×1=12(海里)(等边对等角);
(2)∵CO⊥AB,∠CBO=60°
∴BO=BC×cos∠CBO=12×=6(海里),
6÷12=0.5(小时),
答:如果渔船继续向东航行,需要0.5小时到达距离岛C最近的位置;
(3)∵CO⊥AB,∠CBO=60°
∴CO=BC×sin∠CBO=12×sin60°=6(海里),
∵6>10,
∴如果渔船继续向东航行,没有触礁危险;
3.解:如图,作PD⊥AB交AB延长线于D点,
∵∠PBC=30°,
∴∠PAB=15°,
∴∠APB=∠PBC﹣∠PAB=15°,
∴PB=AB=20×2=40 (海里),
在Rt△BPD中,
∴PD=PB=20(海里),
∵20>18,
∴不会触礁.
4.解:若渔船继续向东航行,无触礁的危险.理由如下:
如图,过点A作AD⊥BC于点D.
由题意得:∠ABD=45°,∠ACD=30°.
设AD=x海里.
在Rt△ABD中,∵∠ABD=45°,
∴BD=AD=x海里.
在Rt△ACD中,∵∠ACD=30°,
∴CD=AD=x海里.
∵BD+DC=30,
∴x+x=30,
解得x=15(﹣1),
15(﹣1)≈10.5海里>8海里,
即:若渔船继续向东航行,无触礁危险.
5.解:作PQ⊥AB于Q,根据已知,∠APQ=30°.
则AQ=AP
∵AP=20×10=200
∴AQ=100
∴PQ==100,
在Rt△BPQ中,sinB=,
∴PB=100÷0.60≈288米
∴此时,小亮与妈妈相距288米.
6.解:(1)如图所示.
则有∠ABD=30°,∠ACD=60°.
∴∠CAB=∠ABD,
∴BC=AC=20海里.
在Rt△ACD中,设CD=x海里,
则AC=2x,AD==x,
在Rt△ABD中,AB=2AD=2x,
BD==3x,
又∵BD=BC+CD,
∴3x=20+x,
∴x=10.
∴AD=x=10≈17.32(海里);
(2)∵17.32海里>17海里,
∴轮船不改变航向继续向前行使,轮船无触礁的危险.
7.解:设东西方向为PQ,则PQ⊥AB,设垂足为Q,
Rt△APQ中,∠APQ=90°﹣60o=30o,
∴AQ=AP=100海里.PQ=AP=100海里.
Rt△PBQ中,∠BPQ=90°﹣45o=45o,
∴BQ=PQ=100海里,
∴AB=(100+100)海里,
答:从A处到B处路程为(100+100)海里.
8.解:如图,过点P作PE⊥AB于点E,
则有∠APE=60°,∠BPE=37°,
在Rt△APE中,∠APE=60°,
∴∠PAE=30°,
∴PE=PA=18,
在Rt△PBE中,
∴PB===22.5,
∵=1.2(小时),22.5÷20=1.125(小时),
所以,船B先到达船P处.
9.解:过点P作PC⊥AB,垂足为C,
根据题意可得出:∠A=60°,∠B=45°,AP=120,
在Rt△APC中,∵cos∠A=,
∴PC=PA cos∠A=60(海里),
在Rt△PCB中,∵∠b=45°,
∴PC=BC,
∴PB=(海里).
答:军舰B与军舰P之间的距离约为60海里.
10.解:(1)如图,∵∠EAB=30°,AE∥BF,
∴∠FBA=30°,
又∵∠FBC=75°,
∴∠ABC=45°
又∵∠BAC=∠BAE+∠CAE=30°+45°=75°,
∴∠ACB=180°﹣45°﹣75°=60°;
(2)如图,作AD⊥BC于D.
在Rt△ABD中,
∵∠ABD=45°,AB=240
∴AD=BD=(海里)
在Rt△ACD中,∵∠C=60°,AD=
∴(海里)
∴BC=BD+CD=+(海里)
答:该船与B港口之间的距离CB的长为(+)海里.
11.解:作PC⊥AB于C点,
∴∠APC=30°,∠BPC=45° AP=80(海里).
在Rt△APC中,cos∠APC=,
∴PC=PA cos∠APC=40(海里).
在Rt△PCB中,cos∠BPC=,
∴PB===40≈98(海里).
答:此时轮船所在的B处与灯塔P的距离是98海里.
12.解:过D作DE⊥AB于点E,
∴四边形BCDE为矩形,
DE=BC=20米,CD=BE=1.6米,
在Rt△ADE中,
∵∠ADE=38.5°,
∴tan∠ADE==tan38.5°=0.795,
∴AE=DE tan38.5°=20×0.795=15.9(米),
∴AB=AE+EB=15.9+1.6=17.5≈18(米).
答:建筑物的高度AB约为18米.
13.解:设CE的长为xm,
在Rt△CBE中,∵∠CBE=45°,
∴∠BCD=45°,
∴CE=BE=xm,
∴AE=AB+BE=40+x(m)
在Rt△ACE中,∵∠CAE=30°,
∴tan30°=
即=,
解得,x=20+20
≈20×1.732+20
=54.64(m)
所以CD=CE+ED
=54.65+1.5=56.15≈56(m)
答:该建筑物的高度约为56m.
14.解:Rt△AFE中,tan∠AFE=tan61°=,
设AE=x,则EF=,
由已知得:CF=DH=15,
Rt△ACE中,tan∠ACE=,
∵∠ACE=42°,
∴tan42°=0.90=,
解得:x=27,
∴AB=BE+AE=1.5+27=28.5≈29;
答:佛像的高度AB是29米.
15.解:∵tanα=,
∴设AB=3a,则BC=4a,
∵tan30°=,即=
解得,a=,
∴AB=3a=≈752,
则小山岗的高AB为752米.
16.解:(1)Rt△ABH中,i=tan∠BAH==,
∴∠BAH=30°,
∴BH=AB=5;
(2)过B作BG⊥DE于G,
由(1)得:BH=5,AH=5,
∴BG=AH+AE=5+15,
Rt△BGC中,∠CBG=45°,
∴CG=BG=5+15.
Rt△ADE中,∠DAE=60°,AE=15,
∴DE=AE=15.
∴CD=CG+GE﹣DE=5+15+5﹣15=20﹣10≈2.7m.
答:宣传牌CD高约2.7米.
17.解:设AB=x米
∵∠C=45°
∴在Rt△ABC中,BC=AB=x米,
∵∠ADB=60°,
又∵CD=6米,
∴在Rt△ADB中
tan∠ADB=
tan60°=
解得
答,建筑物的高度为14.2米.
18.解:(1)作AE⊥CD于点E,
设CE=x,
在Rt△ACE中,∠CAE=30°,则AE=x,可得BD=AE=x;
在Rt△BCD中,∠CBD=60°,则CD=BD=3x,
∵CD=CE+DE,
∴3x=30+x,
解得:x=15,
∴BD=15(米),
答:甲、乙两建筑物之间的距离BD为15米;
(2)由(1)知,CD=3x=45(米),
答:乙建筑物的高CD为45米.
19.解:作BF⊥CD于点F,设DF=x米,
在Rt△DBF中,tan∠DBF=,
则BF===x,
在直角△DCE中,DC=x+CF=3+x(米),
在直角△DCE中,tan∠DEC=,则EC===(x+3)米.
∵BF﹣CE=AE,即x﹣(x+3)=18.
解得:x=9+,
则CD=9++3=9+(米).
答:CD的高度是(9+)米.
20.解:过A作AE⊥BC,交CB的延长线于点E,
在Rt△ACD中,
∵∠CAD=30°,AD=420米,
∴CD=AD tan30°=420×=140(米),
∴AE=CD=140米.
在Rt△ABE中,
∵∠BAE=30°,AE=140米,
∴BE=AE tan30°=140×=140(米),
∴BC=AD﹣BE=420﹣140=280(米),
答:这栋楼的高度为280米.
21.解:设DB=xm,
在Rt△ADB中,AB=xtan60°=xm,
在Rt△ACB中,=tan30°,即=,
整理得,3x=x+20,
解得,x=10,
则AB=10m.
故建筑物AB的高度是10m.
1.一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以80海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上,求此时货轮距灯塔A的距离AB(结果保留3个有效数字,≈2.449).
2.如图,某渔船向正东方向以12海里时的速度航行,在A处测得岛C在北偏东的60°方向,1小时后渔船航行到B处,测得岛C在北偏东的30°方向,已知该岛周围10海里内有暗礁.
(1)B处离岛C有多远?
(2)如果渔船继续向东航行,需要多长时间到达距离岛C最近的位置?
(3)如果渔船继续向东航行,有无触礁危险?
3.一艘轮船由南向北航行,如图,在A处测得小岛P在北偏西15°方向上,两个小时后,轮船在B处测得小岛P在北偏西30°方向上,在小岛周围18海里内有暗礁,问若轮船按20海里/时的速度继续向北航行,有无触礁的危险?
4.如图,某渔船向正东方向航行,在B处测得A岛在北偏东的45°方向,岛C在B处的正东方向且相距30海里,从岛C测得A岛在北偏西的60°方向,已知A岛周围8海里内有暗礁.如果渔船继续向东航行,有无触礁危险?(≈1.4,≈1.7)
5.小亮一家到桃林口水库游玩.在岸边码头P处,小亮和爸爸租船到库区游玩,妈妈在岸边码头P处观看小亮与爸爸在水面划船,小船从P处出发,沿北偏东60°方向划行,划行速度是20米/分钟,划行10分钟后到A处,接着向正南方向划行一段时间到B处,在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米?(精确到1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41,≈1.73)
6.如图,一艘轮船航行到B处时,测得小岛A在船的北偏东60°的方向,轮船从B处继续向正东方向航行20海里到达C处时,测得小岛A在北船的北偏东30°的方向.
(1)若小岛A到这艘轮船航行路线BC的距离是AD,求AD的长.
(2)已知在小岛周围17海里内有暗礁,若轮船不改变航向继续向前行驶,试问轮船有无触礁的危险?(≈1.732)
7.如图,某测量船位于海岛P的北偏西60°方向,距离海岛200海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的西南方向上的B处.求测量船从A处航行到B处的路程(结果保留根号).
8.如图,在东西方向的海岸线MN上有A,B两艘船,船长都收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向36海里处,船P在船B顶点北偏西37°方向,若船A,船B分别以30海里/小时,20海里/小时的速度同时出发,匀速前往救援,通过计算判断哪艘船先到达船P处.(参考数据=1.73,sin37°=0.6,cos37°=0.80)
9.4月12日上午,蓝鲸凌波,战舰驰骋,银鹰翱翔,中央军委在南海某海域举行海上阅兵,如图,军舰位于军舰P的北偏东60°方向上,两舰的距离为120海里,军舰B位于军舰A的正南方向,军舰P的南偏东45°方向上,求军舰B与军舰P之间的距离(结果保留根号).
10.某海域有A、B两个港口,B港口在A港口北偏西30°方向上,距A港口240海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求:
(1)∠ACB的度数;
(2)此时刻船与B港口之间的距离CB的长(结果保留根号).
11.如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:≈2.449,结果保留整数)
12.如图,为测量某建筑物AB的高度,在离该建筑物底部20m的点C处,目测建筑物顶端A处,视线与水平线夹角∠ADE为38.5°,目高CD为1.6m.求建筑物AB的高度.(结果精确到1m)
【参考数据:sin38.5°=0.623,cos38.5°=0.783,tan38.5°=0.795】
13.如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了40m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(结果精确到1m)(参考数据:≈1.732,≈1.414)
14.敦煌莫高窟是甘肃省敦煌市境内的莫高窟、西千佛洞的总称,是我国著名的四大石窟之一,也是世界上现存规模最宏大、保存最完好的佛教艺术宝库,数学课外实践活动中,小明为测量莫高窟内佛像高度,分别在点D、H处用高为1.5米的测角仪对佛像进行了测量,如图,测得∠ACE=42°,∠AFE=61°,若DH=15米,求佛像的高度AB.(结果精确到1米,参考数据sin42°≈0.67,tan42°≈0.90,sin61°≈0.87,tan61°≈1.80)
15.如图,小山岗的斜坡AC的坡度是tanα=,在与山脚C水平距离300米的D处,测得山顶A的仰角为30°,点B、C、D在同一条直线上,求小山岗的高AB(结果保留整数或保留精确值)(参考数据≈1.732)
16.如图,某大楼的顶部竖有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:≈1.414,≈1.732)
17.某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端A处,测得仰角为45°,再往建筑物的方向前进6米到达D处,测得仰角为60°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米,≈1.732,≈1.414)
18.如图,线段AB、CD分别表示在同一水平线上的甲、乙两建筑物的高,AB⊥BD,CD⊥BD,垂足分别为B、D.从B点测到C点的仰角α为60°,从A点测得C点的仰角β为30°,甲建筑物的高AB=30米.
(1)求甲、乙两建筑物之间的距离BD.
(2)求乙建筑物的高CD.
19.如图,斜坡BE,坡顶B到水平地面的距离AB为3米,坡底AE为18米,在B处,E处分别测得CD顶部点D的仰角为30°,60°,求CD的高度.(结果保留根号)
20.热气球的探测器显示,从热气球底部a处看一栋高楼顶部的俯角为30°,看这栋楼底部俯角为60°,热气球a处与地面距离为420米,求这栋楼的高度.
21.某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进20m到达点D处,又测得点A的仰角为60°,则建筑物AB的高度是多少m?(结果用根式表示)
参考答案
1.解:由示意图可知:∠ACB=60°,
由平行线的性质可知∠ABC=180°﹣30°﹣75°=75°,
则∠A=180°﹣∠C﹣∠B=45°,BC=80×=40(海里),
过B作BD⊥AC于点D,
则∠BDC=90°,∠DBC=30°,
∴DC=BC=20海里,
由勾股定理得:BD=20海里,
∵∠A=45°,∠ADB=90°,
∴∠ABD=∠A=45°,
∴AD=BD=20海里,
由勾股定理得:AB===20≈49.0(海里),
答:此时货轮距灯塔A的距离AB为49.0海里.
2.解:(1)过C作CO⊥AB于O,则CO为渔船向东航行到C道最短距离,
∵在A处测得岛C在北偏东的60°,
∴∠CAB=30°,
又∵B处测得岛C在北偏东30°,
∴∠CBO=60°,∠ABC=120°,
∴∠ACB=∠CAB=30°,
∴AB=BC=12×1=12(海里)(等边对等角);
(2)∵CO⊥AB,∠CBO=60°
∴BO=BC×cos∠CBO=12×=6(海里),
6÷12=0.5(小时),
答:如果渔船继续向东航行,需要0.5小时到达距离岛C最近的位置;
(3)∵CO⊥AB,∠CBO=60°
∴CO=BC×sin∠CBO=12×sin60°=6(海里),
∵6>10,
∴如果渔船继续向东航行,没有触礁危险;
3.解:如图,作PD⊥AB交AB延长线于D点,
∵∠PBC=30°,
∴∠PAB=15°,
∴∠APB=∠PBC﹣∠PAB=15°,
∴PB=AB=20×2=40 (海里),
在Rt△BPD中,
∴PD=PB=20(海里),
∵20>18,
∴不会触礁.
4.解:若渔船继续向东航行,无触礁的危险.理由如下:
如图,过点A作AD⊥BC于点D.
由题意得:∠ABD=45°,∠ACD=30°.
设AD=x海里.
在Rt△ABD中,∵∠ABD=45°,
∴BD=AD=x海里.
在Rt△ACD中,∵∠ACD=30°,
∴CD=AD=x海里.
∵BD+DC=30,
∴x+x=30,
解得x=15(﹣1),
15(﹣1)≈10.5海里>8海里,
即:若渔船继续向东航行,无触礁危险.
5.解:作PQ⊥AB于Q,根据已知,∠APQ=30°.
则AQ=AP
∵AP=20×10=200
∴AQ=100
∴PQ==100,
在Rt△BPQ中,sinB=,
∴PB=100÷0.60≈288米
∴此时,小亮与妈妈相距288米.
6.解:(1)如图所示.
则有∠ABD=30°,∠ACD=60°.
∴∠CAB=∠ABD,
∴BC=AC=20海里.
在Rt△ACD中,设CD=x海里,
则AC=2x,AD==x,
在Rt△ABD中,AB=2AD=2x,
BD==3x,
又∵BD=BC+CD,
∴3x=20+x,
∴x=10.
∴AD=x=10≈17.32(海里);
(2)∵17.32海里>17海里,
∴轮船不改变航向继续向前行使,轮船无触礁的危险.
7.解:设东西方向为PQ,则PQ⊥AB,设垂足为Q,
Rt△APQ中,∠APQ=90°﹣60o=30o,
∴AQ=AP=100海里.PQ=AP=100海里.
Rt△PBQ中,∠BPQ=90°﹣45o=45o,
∴BQ=PQ=100海里,
∴AB=(100+100)海里,
答:从A处到B处路程为(100+100)海里.
8.解:如图,过点P作PE⊥AB于点E,
则有∠APE=60°,∠BPE=37°,
在Rt△APE中,∠APE=60°,
∴∠PAE=30°,
∴PE=PA=18,
在Rt△PBE中,
∴PB===22.5,
∵=1.2(小时),22.5÷20=1.125(小时),
所以,船B先到达船P处.
9.解:过点P作PC⊥AB,垂足为C,
根据题意可得出:∠A=60°,∠B=45°,AP=120,
在Rt△APC中,∵cos∠A=,
∴PC=PA cos∠A=60(海里),
在Rt△PCB中,∵∠b=45°,
∴PC=BC,
∴PB=(海里).
答:军舰B与军舰P之间的距离约为60海里.
10.解:(1)如图,∵∠EAB=30°,AE∥BF,
∴∠FBA=30°,
又∵∠FBC=75°,
∴∠ABC=45°
又∵∠BAC=∠BAE+∠CAE=30°+45°=75°,
∴∠ACB=180°﹣45°﹣75°=60°;
(2)如图,作AD⊥BC于D.
在Rt△ABD中,
∵∠ABD=45°,AB=240
∴AD=BD=(海里)
在Rt△ACD中,∵∠C=60°,AD=
∴(海里)
∴BC=BD+CD=+(海里)
答:该船与B港口之间的距离CB的长为(+)海里.
11.解:作PC⊥AB于C点,
∴∠APC=30°,∠BPC=45° AP=80(海里).
在Rt△APC中,cos∠APC=,
∴PC=PA cos∠APC=40(海里).
在Rt△PCB中,cos∠BPC=,
∴PB===40≈98(海里).
答:此时轮船所在的B处与灯塔P的距离是98海里.
12.解:过D作DE⊥AB于点E,
∴四边形BCDE为矩形,
DE=BC=20米,CD=BE=1.6米,
在Rt△ADE中,
∵∠ADE=38.5°,
∴tan∠ADE==tan38.5°=0.795,
∴AE=DE tan38.5°=20×0.795=15.9(米),
∴AB=AE+EB=15.9+1.6=17.5≈18(米).
答:建筑物的高度AB约为18米.
13.解:设CE的长为xm,
在Rt△CBE中,∵∠CBE=45°,
∴∠BCD=45°,
∴CE=BE=xm,
∴AE=AB+BE=40+x(m)
在Rt△ACE中,∵∠CAE=30°,
∴tan30°=
即=,
解得,x=20+20
≈20×1.732+20
=54.64(m)
所以CD=CE+ED
=54.65+1.5=56.15≈56(m)
答:该建筑物的高度约为56m.
14.解:Rt△AFE中,tan∠AFE=tan61°=,
设AE=x,则EF=,
由已知得:CF=DH=15,
Rt△ACE中,tan∠ACE=,
∵∠ACE=42°,
∴tan42°=0.90=,
解得:x=27,
∴AB=BE+AE=1.5+27=28.5≈29;
答:佛像的高度AB是29米.
15.解:∵tanα=,
∴设AB=3a,则BC=4a,
∵tan30°=,即=
解得,a=,
∴AB=3a=≈752,
则小山岗的高AB为752米.
16.解:(1)Rt△ABH中,i=tan∠BAH==,
∴∠BAH=30°,
∴BH=AB=5;
(2)过B作BG⊥DE于G,
由(1)得:BH=5,AH=5,
∴BG=AH+AE=5+15,
Rt△BGC中,∠CBG=45°,
∴CG=BG=5+15.
Rt△ADE中,∠DAE=60°,AE=15,
∴DE=AE=15.
∴CD=CG+GE﹣DE=5+15+5﹣15=20﹣10≈2.7m.
答:宣传牌CD高约2.7米.
17.解:设AB=x米
∵∠C=45°
∴在Rt△ABC中,BC=AB=x米,
∵∠ADB=60°,
又∵CD=6米,
∴在Rt△ADB中
tan∠ADB=
tan60°=
解得
答,建筑物的高度为14.2米.
18.解:(1)作AE⊥CD于点E,
设CE=x,
在Rt△ACE中,∠CAE=30°,则AE=x,可得BD=AE=x;
在Rt△BCD中,∠CBD=60°,则CD=BD=3x,
∵CD=CE+DE,
∴3x=30+x,
解得:x=15,
∴BD=15(米),
答:甲、乙两建筑物之间的距离BD为15米;
(2)由(1)知,CD=3x=45(米),
答:乙建筑物的高CD为45米.
19.解:作BF⊥CD于点F,设DF=x米,
在Rt△DBF中,tan∠DBF=,
则BF===x,
在直角△DCE中,DC=x+CF=3+x(米),
在直角△DCE中,tan∠DEC=,则EC===(x+3)米.
∵BF﹣CE=AE,即x﹣(x+3)=18.
解得:x=9+,
则CD=9++3=9+(米).
答:CD的高度是(9+)米.
20.解:过A作AE⊥BC,交CB的延长线于点E,
在Rt△ACD中,
∵∠CAD=30°,AD=420米,
∴CD=AD tan30°=420×=140(米),
∴AE=CD=140米.
在Rt△ABE中,
∵∠BAE=30°,AE=140米,
∴BE=AE tan30°=140×=140(米),
∴BC=AD﹣BE=420﹣140=280(米),
答:这栋楼的高度为280米.
21.解:设DB=xm,
在Rt△ADB中,AB=xtan60°=xm,
在Rt△ACB中,=tan30°,即=,
整理得,3x=x+20,
解得,x=10,
则AB=10m.
故建筑物AB的高度是10m.
