鲁教版(五四制)2021-2022学年九年级数学下册5.2圆的对称性 同步练习题(word版、含解析)
文档属性
| 名称 | 鲁教版(五四制)2021-2022学年九年级数学下册5.2圆的对称性 同步练习题(word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 656.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 16:20:48 | ||
图片预览




文档简介
2021-2022学年鲁教版九年级数学下册《5.2圆的对称性》同步练习题(附答案)
1.如图,点A,B,C,D都在⊙O上,圆的半径为2,且CB=CD=2,AB=AD,则该S四边形ABCD=( )
A.4 B.2 C.3 D.6
2.如图,AB是圆O的直径,弦AD,BC相交于点P,∠DPB=60°,D是的中点,则的值是( )
A. B.2 C. D.
3.一个圆的内接正多边形中,一边所对的中心角为72°,则该正多边形的边数是( )
A.6 B.5 C.4 D.3
4.一条弦将圆分成1:4两部分,那么这条弦所对的圆心角为( )
A.60° B.72° C.90° D.108°
5.如图,在⊙O中,AB是弦,C是弧AB上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的度数为( )
A.30° B.40° C.50° D.60°
6.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AC=12,AE=3,则⊙O的直径长为( )
A.10 B.13 C.15 D.16
7.如图,半径为R的⊙O的弦AC=BD.且AC⊥BD于E,连接AB,AD,若AD=2,则半径R的长为( )
A.1 B. C.2 D.2
8.如图,A,B在半径为的⊙O上,将沿着弦AB翻折,若∠AOB=150°,则图中月牙(阴影)的面积等于( )
A.π﹣3 B.π+3 C.2π﹣3 D.π
9.以下命题:①直径是弦; ②长度相等的弧是等弧; ③相等的弦所对的弧也相等; ④圆的对称轴是直径;其中正确的个数是( )
A.4 B.3 C.2 D.1
10.如图,四边形ABCD内接于半圆O,AB为直径,AB=4,AD=DC=1,则弦BC的长为( )
A.3.5 B.2 C. D.
11.如图:AB为半圆的直径,AB=4,C为OA中点,D为半圆上一点,连CD,E为的中点,且CD∥BE,则CD的长为( )
A. B. C. D.
12.如图,OA,OB,OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC.则下列结论正确的是( )
A.AB=2BC B.AB<2BC C.∠AOB=2∠CAB D.∠ACB=4∠CAB
13.如图,四边形ABCD中,连接AC、BD,点O为AB的中点,若∠ADB=∠ACB=90°,则下面结论不一定正确的是( )
A.DC=CB
B.∠DAC=∠DBC
C.∠BCD+∠BAD=180°
D.点A、C、D到点O的距离相等
14.将一个半径为1的圆形轮子沿直线l水平向右滚动,图中显示的是轮子上的点P的起始位置与终止位置,其中在起始位置时PO∥l,在终止位置时PO与l所夹锐角为60°,则滚动前后,圆心之间的距离可能为( )
A. B. C.π D.
15.如图,AB是⊙O的直径,M、N分别是AO,BO的中点,CM⊥AB,DN⊥AB,则的度数 .
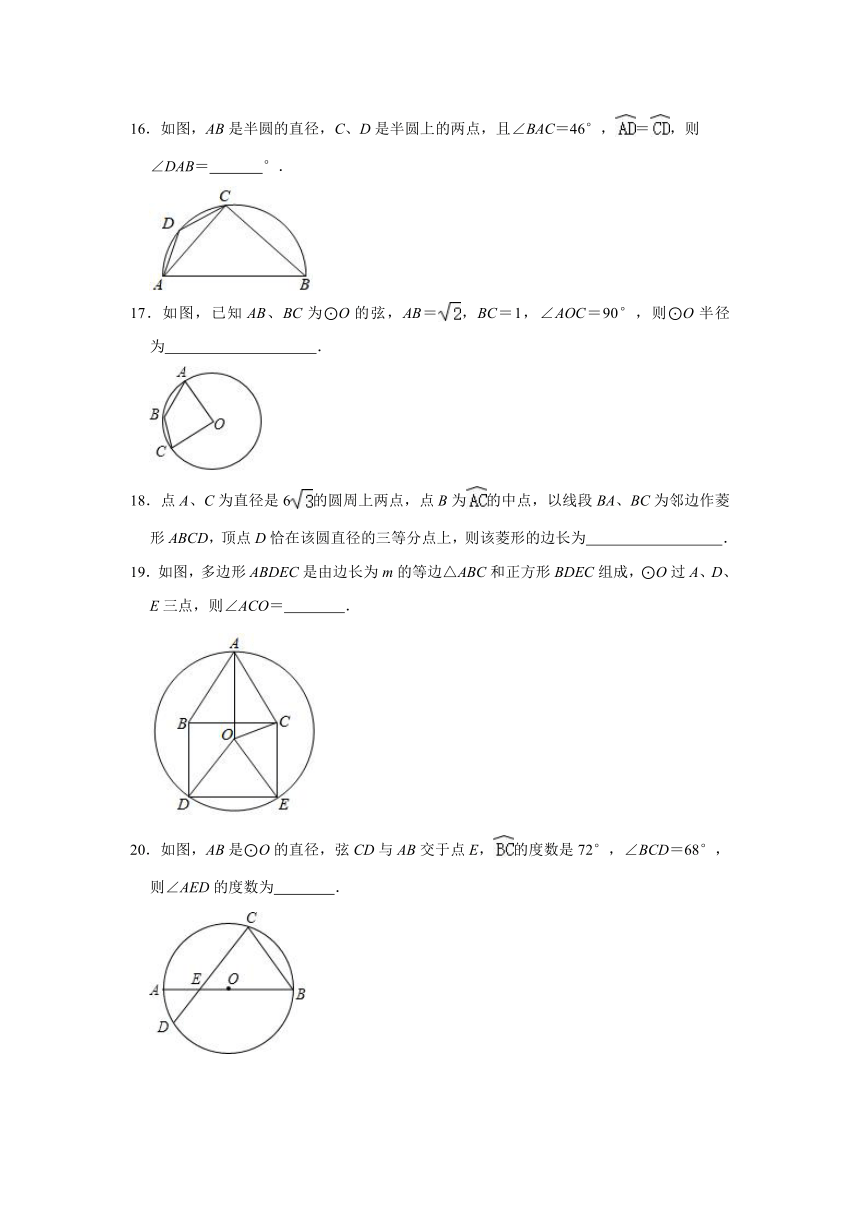
16.如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=46°,=,则
∠DAB= °.
17.如图,已知AB、BC为⊙O的弦,AB=,BC=1,∠AOC=90°,则⊙O半径为 .
18.点A、C为直径是6的圆周上两点,点B为的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为 .
19.如图,多边形ABDEC是由边长为m的等边△ABC和正方形BDEC组成,⊙O过A、D、E三点,则∠ACO= .
20.如图,AB是⊙O的直径,弦CD与AB交于点E,的度数是72°,∠BCD=68°,则∠AED的度数为 .
21.如图,在扇形AOB中,∠AOB=60°,AO=6,点D为的中点,C为半径OA上一动点(点A除外),沿CD对折后点A恰好落在扇形AOB的边线OB或OA上,AC的长可以是 .
22.如图.点A、B把⊙O分成2:7两条弧,则∠AOB= .
23.已知圆O的半径长为6,若弦AB=6,则弦AB所对的圆心角等于 .
24.如图,△ABC内接于⊙O,AB=AC,点E,F分别在和上,若∠ABC=50°,则∠BEC= °,∠BFC= °.
25.如图,扇子的圆心角为α,余下扇形的圆心角为β,为了使扇子的外形美观,通常情况下α与β的比按黄金比例设计,若取黄金比为0.6,则α= 度.
26.如图,在⊙O中,若==,则AC与2CD的大小关系是:AC 2CD.(填“>”,“<”或“=”)
27.如图所示,四边形AB∥CD,AD=DC=DB=p,BC=q,则AC= (用p、q表示).
28.如图,已知⊙O的半径为30mm,弦AB=36mm,则sin∠OAB= .
29.如图,等腰△ABC的顶角∠A=40°,以AB为直径的半圆与BC、AC分别交于D、E两点,则∠EBC= ,的度数为 .
30.如下图,弦CD、FE的延长线交于圆外点P,割线PAB经过圆心,请你结合现有图形,添加一个适当的条件: ,使结论∠1=∠2能成立.
31.如图,在⊙O中,点C为劣弧AB的中点,连接AC并延长至D,使CA=CD,连接DB并延长交⊙O于点E,连接AE.若BE,BD的长度分别是方程x2﹣5x+6=0的两个解,则△AED中,DE边上的高的长度为 .
32.如图,在⊙O中,两弦AD∥BC,AC,BD相交于点E,连接AB,CD,图中的全等三角形共有 对.相似比不等于1的相似三角形共有 对.
33.如图,在⊙O中,=,∠A=30°,则∠B= °.
34.如图,以Rt△ABC的直角顶点为圆心,以BA为半径的圆分别交AC于点D,交BC于点E.若∠C=31°,求的度数.
35.如图,已知AB是半径为1的圆O的一条弦,且AB<1,以AB为一边在圆O内作正△ABC,点D为圆O上不同于点A的一点,且DB=AB,DC的延长线交圆O于点E,试探究AE的长是否为定值(不随AB长度的变化而变化)?若为定值,求出这个定值;若不为定值,试确定AE与OA长之间的关系. .
36.如图,AB、CD是⊙O的直径,弦CE∥AB,所对的圆心角为30°.求∠AOC的度数.
37.如图,MB,MD是⊙O的两条弦,点A,C分别在,上,且AB=CD,M是的中点.
(1)求证:MB=MD;
(2)过O作OE⊥MB于点E,当OE=1,MD=4时,求⊙O的半径.
38.如图,在⊙O中,弦AB与DC相交于E,且BE=DE,求证:=.
39.如图,A、B、C、D是⊙O上四点,且AB=CD,求证:AD=BC.
40.如图,A,B,C,D在⊙O上,若AC=BD,求证:BC=AD.
参考答案
1.解:连接AC,
∵CB=CD,AD=AB,
∴=,=,
∴=,
即AC是圆的直径,
∴∠D=∠B=90°,
∵圆的半径为2,
∴AC=4,
∵CB=CD=2,
由勾股定理得:AD=AB==2,
∴S四边形ABCD
=S△ADC+S△ABC
=+
=+
=4,
故选:A.
2.解:∵AB是圆O的直径,
∴∠ACB=90°.
而∠DPB=60°,
∴∠APC=60°.
∴∠CAD=30°.
又∵D是的中点,
∴∠CAD=∠BAD=30°.
∴∠ABC=180°﹣30°﹣30°﹣90°=30°.
∴=.
故选:A.
3.解:设正多边形的边数为n.
由题意=72°,
∴n=5,
故选:B.
4.解:弦所对的圆心角=劣弧所对的圆心角=×360°=72°.
故选:B.
5.解:∵OA=OB,∠OAB=25°,
∴∠OBA=∠OAB=25°,
∴∠AOB=180°﹣∠OAB﹣∠OBA=130°,
∵OA=OC,∠OCA=40°,
∴∠OAC=∠OCA=40°,
∴∠AOC=180°﹣∠OAC﹣∠OCA=100°,
∴∠BOC=∠AOB﹣∠AOC=130°﹣100°=30°,
故选:A.
6.解:如图,连接OF.
∵DE⊥AB,
∴DE=EF,=,
∵点D是弧AC的中点,
∴=,
∴=,
∴AC=DF=12,
∴EF=DF=6,设OA=OF=x,
在Rt△OEF中,则有x2=62+(x﹣3)2,
解得x=,
∴AB=2x=15,
故选:C.
7.解:连接OA,OD,
∵弦AC=BD,
∴=,
∴=,
∴∠ABD=∠BAC,
∴AE=BE,
∵AC⊥BD,AE=BE,
∴∠ABE=∠BAE=45°,
∴∠AOD=2∠ABE=90°,
∵OA=OD,
∴AD=R,
∵AD=2,
∴R=2,
故选:C.
8.解:如图,作BD⊥AO交AO于点D.
∵OA=OB,∠AOB=150°,
∴∠DOB=30°,
∵OB=,
∴BD=OB=,
S阴=S圆O﹣2 S弓形AmB=π ()2﹣2(﹣××)=6π﹣5π+3=π+3,
故选:B.
9.解:①直径是弦,是真命题;
②在同圆或等圆中,长度相等的弧是等弧,原命题是假命题;
③在同圆或等圆中,相等的弦所对的弧也相等,原命题是假命题;
④圆的对称轴是直径所在的直线,原命题是假命题;
故选:D.
10.解:如图,连AC、BD,过D作DE⊥AC于E.
∴∠ADB=∠ACB=90°,∠ABD=∠CAD.
∵BD==.
∵AD=DC=1,
∴∠DAC=∠DCA,
∵∠DCA=∠ABD,
cos∠CAD=cos∠ABD==.
∴AE=AD cos∠CAD=,
∴AC=2AE=,
∴BC==.
故选:A.
11.解:如图,连接EO并延长与DC的延长线相交于点K,连接BD交OE于点H,
∵E为弧AD中点,
∴OE⊥AD,BH=DH,
∵BE∥CD,
∴∠EBH=∠KDH,∠E=∠K,
∴△BHE≌△DHK(AAS),
∴BE=KD=2x,EH=KH,
∵BE∥CD,
∴△KCO∽△EBO,
∴,
∵AB是半圆⊙O的直径,AB=4,C为OA的中点,
∴,
∴KO=1,KC=x,
∴KE=KO+OE=1+2=3,
∴EH=KH=1.5,OH=0.5,
∵BE2﹣EH2=BH2=BO2﹣OH2,
∴4x2﹣1.52=22﹣0.52,
解得:x=,
∴CD=KD﹣KC=2x﹣x=x=,
故选:B.
12.解:取的中点D,连接AD,BD,
∵∠AOB=2∠BOC,
∴=2,
∴==,
∴AD=BD=BC,
∵AB<AD+BD,
∴AB<2BC.故A错误,B正确;
∵∠AOB=2∠BOC,∠BOC=2∠CAB,
∴∠AOB=4∠CAB;故C错误;
∵∠AOB=2∠ACB,
∴∠ACB=∠BOC=2∠CAB,故D错误.
故选:B.
13.解:∵点O为AB的中点,∠ADB=∠ACB=90°,
∴D,C在以O为圆心,AB为直径的圆上,如图,
∴∠DAC=∠DBC,∠BCD+∠BAD=180°,点A、C、D到点O的距离相等,
当∠DAC=∠BAC时,DC=CB,而题目中未给出.
故选:A.
14.解:由题意可得,圆形轮子可能滚动不止一周,设OP滚动了n周后又滚动120°后到达终止位置,
∴OP滚动的角度α=120°+360n,n为整数,
可得圆心运动前后的距离即为OP滚动完毕扫过的角度所对应的弧长,
即为2πr×=,n为整数.
当n=0时为.
故选:B.
15.解:∵AB是⊙O的直径,M、N分别是AO,BO的中点,
∴2OM=OC,2ON=OD,
∵CM⊥AB,DN⊥AB,
∴∠CMO=∠DNO=90°,
∴∠MCO=∠NDO=30°,
∴∠MOC=∠NOD=60°,
∴∠COD=180°﹣60°﹣60°=60°,
∴的度数是60°,
故答案为:60°
16.解:∵AB是半圆O的直径,
∴∠ACB=90°,
∵∠BAC=46°,
∴∠B=44°.
∴∠ADC=180°﹣44°=136°.
∵=,
∴AD=DC.
∴∠DAC=∠DCA==22°,
∴∠BAD=∠DAC+∠BAC=22°+46°=68°.
故答案是:68.
17.解:作AH⊥CB交CB的延长线于H,连接AC.
由∠AOC=90°,可得∠ABC=135°,
在Rt△AHB中,∵AB=,∠ABH=45°,
∴AH=BH=1,
在Rt△AHC中,∵CH=CB+BH=2,AH=1,
∴AC==,
∵OA=OC,∠AOC=90°,
∴OA=OC=,
故答案为.
18.解:过B作直径,连接AC交AO于E,
∵点B为的中点,
∴BD⊥AC,
如图①,
∵点D恰在该圆直径的三等分点上,
∴BD=×6=2,
∴OD=OB﹣BD=,
∵四边形ABCD是菱形,
∴DE=BD=,
∴OE=2,
连接OC,
∵CE=,
∴边CD=;
如图②,BD=×6=4,
同理可得,OD=,OE=,DE=2,
连接OC,
∵CE=,
∴边CD=,
故答案为6或3.
19.解:∵多边形ABDEC是由边长为m的等边△ABC和正方形BDEC组成,
∴AC=EC,∠ACE=∠ACB+∠ECB=60°+90°=150°,
∵⊙O过A,D,E三点,
∴AO=EO,
又OC=OC,
∴△ACO≌ECO(SSS),
∴∠ACO=∠ECO=∠ACE=1/2×150°=75°,
故答案为:75°.
20.解:∵AB是⊙O的直径,的度数是72°,
∴=180°﹣72°=108°,
∴∠ABC==×108°=54°,
∵∠BCD=68°,
∴∠CEB=180°﹣∠BCD﹣∠ABC=180°﹣68°﹣54°=58°.
故答案为:58°.
21.解:①当点E落在半径OA上时,连接OD,如图1所示,
∵∠ACD=90°,∠AOB=60°,点D为弧AB的中点,点A(2,0),
∴∠COD=30°,OA=OD=6,
∴OC=OD cos30°=6×=3,
∴AC=OA﹣OC=6﹣3;
②如图2,沿CD对折后点A恰好落在边线OB上,且A′和B重合时,
则C和O重合,此时,AC=OA=6;
③沿CD对折后点A恰好落在边线OB上,且A′和B不重合时,如图3;
连接OD、BD、AD,作DF⊥OA于F,
∵∠AFD=90°,∠AOB=60°,点D为弧AB的中点,
∴∠AOD=∠BOD=30°,∠OAD=∠OBD,
∵OA=OD=6,
∴DF=OD sin30°=6×=3,∠OAD=75°,
∴OF=OD cos30°=6×=3,
∴AF=OA﹣OD=6﹣3,
∵DA′=DA=DB,∠OAD=∠OBD=75°,
∴BA′=2AF=12﹣6,∠DA′B=∠OBD=75°,
∴OA′=OB﹣BA′=6﹣(12﹣6)=6﹣6,
∵∠CA′D=∠CAD=75°,
∴∠BA′C=150°,
∴∠OA′C=30°,
∴∠A′CO=90°,
∴CA′=OA′ sin60°=(6﹣6)×=9﹣3,
∴AC=CA′=9﹣3.
故答案为:6﹣3或6或9﹣3.
22.解:∠AOB的度数=×360°=80°.
故答案为80°.
23.解:如图,作OC⊥AB于C,连接OA、OB,
则AC=BC=AB=3,
在Rt△AOC中,OC==3,
∴OC=OA,
∴∠A=30°,
∴∠AOB=180°﹣30°﹣30°=120°.
∴弦AB所对的圆心角的度数为120°.
故答案为120°.
24.解:∵∠ABC=50°,AB=AC,∴∠ABC=∠ACB=50°,
∴∠A=80°,∴∠BEC=80°,
∴∠F=180°﹣80°=100°.
故答案为:80°;100°.
25.解:∵∠α+∠β=360°,且∠α:∠β=0.6,
∴∠β=360°÷1.6=225°,∠α=360°﹣225°=135°.
故本题答案为:135°.
26.解:如图,连接AB、BC,
在⊙O中,若==,
∴AB=BC=CD,
在△ABC中,AB+BC>AC.
∴AC<2CD.
故答案是:<.
27.解:延长CD交半径为p的⊙D于E点,连接AE.显然A、B、C在⊙D上.
∵AB∥CD
∴=,
∴BC=AE=q.
在△ACE中,∠CAE=90°,CE=2p,AE=q,
故AC==.
故答案为:.
28.解:过O作OC⊥AB于C,
∵OC⊥AB,OC过O,AB=36cm,
∴AC=BC=AB=18cm,
在Rt△OCA中,由勾股定理得:OA2=OC2+AC2,
302=OC2+182,
OC=24(cm),负数舍去;
所以sin∠OAB===,
故答案为:.
29.解:连AD,如图,
∵AB为直径,
∴∠ADB=90°,即AD⊥BC,
又∵AB=AC,
∴AD平分∠BAC,
而∠A=40°,
∴∠BAD=∠DAC=20°,
∴∠EBC=∠DAC=20°,
∴弧BD的度数=弧DE的度数=2×20°=40°,
∴弧AE的度数=180°﹣40°﹣40°=100°.
故答案为20°,100°.
30.解:使∠1=∠2能成立,则应有△COP≌△EOP,或△PDB≌△PFB,故可添加AC=AE或BD=BF当AC=AE时,
根据圆周角定理知,∠AOC=∠AOE,∵OC=OE,PO=PO,∴△COP≌△EOP,∴∠1=∠2.
31.解:如图,连接AB,EC.
∵AB是直径,
∴∠ABE=∠ACE=90°,
即EC⊥AD,AB⊥DE,
∵AC=CD,
∴EA=ED,
∵BE,BD的长度分别是方程x2﹣5x+6=0的两个解,
∴BE=2,BD=3或BE=3,BD=2,
当BE=2,BD=3时,EA=BD=5,
∴AB===,
当BE=2,BD=3时,EA=BD=5,
∴AB===4,
综上所述,或4.
32.解:由题意可得全等三角形共有三对,分别为:△ABE≌△DCE、△ABD≌△DCA、△ABC≌△DCB
相似三角形有一对,为△ADE∽△CBE.
33.解:∵在⊙O中,=,
∴AB=AC,
∴△ABC是等腰三角形,
∴∠B=∠C;
又∠A=30°,
∴∠B==75°(三角形内角和定理).
故答案是:75.
34.解:连接BD.
在Rt△ABC中,∵∠ABC=90°,∠C=31°,
∴∠A=90°﹣31°=59°,
∵BA=BD,
∴∠A=∠ADB=59°,
∴∠ABD=180°﹣∠A﹣∠ADB=180°﹣2×59°=62°,
∴∠DBE=90°﹣∠ABD=90°﹣62°=28°,
∴的度数为28°.
35.解:由A、B、D、E四点共圆,
∴∠EAB+∠EDB=180°,
∵BC=BD,∠BDC=∠BCD,∠BCD+∠ECB=180°,
∴∠ECB=∠EAB
又∵∠CAB=∠ACB=60°
∴∠ECB﹣∠ACB=∠EAB﹣∠CAB,
∴∠ECA=∠EAC,
∴△EAC是等腰三角形,
∵AB=BD,
∴∠DEA=∠DOB,
∵AC=AB,
∴△EAC≌△OAB,
∴AE=OA=1.
36.解:连接OE,如图,
∵为30°,
∴∠COE=30°,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OCE=(180°﹣30°)÷2=75°,
∵弦CE∥AB,
∴∠AOC=∠OCE=75°.
37.(1)证明:∵AB=CD,
∴=,
∵M是的中点,
∴=,
∴=,
∴BM=DM.
(2)解:如图,连接OM.
∵DM=BM=4,OE⊥BM,
∴EM=BE=2,
∵OE=1,∠OEM=90°,
∴OM===,
∴⊙O的半径为.
38.证明:在△AED和△CEB中,
,
∴△AED≌△CEB(AAS).
∴AD=BC,
∴=.
39.证明:∵AB=CD,
∴=,
∴+=+,
∴=,
∴AD=BC.
40.证明:∵AC=BD,
∴=.
∴﹣=﹣.即=.
∴BC=AD.
1.如图,点A,B,C,D都在⊙O上,圆的半径为2,且CB=CD=2,AB=AD,则该S四边形ABCD=( )
A.4 B.2 C.3 D.6
2.如图,AB是圆O的直径,弦AD,BC相交于点P,∠DPB=60°,D是的中点,则的值是( )
A. B.2 C. D.
3.一个圆的内接正多边形中,一边所对的中心角为72°,则该正多边形的边数是( )
A.6 B.5 C.4 D.3
4.一条弦将圆分成1:4两部分,那么这条弦所对的圆心角为( )
A.60° B.72° C.90° D.108°
5.如图,在⊙O中,AB是弦,C是弧AB上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的度数为( )
A.30° B.40° C.50° D.60°
6.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AC=12,AE=3,则⊙O的直径长为( )
A.10 B.13 C.15 D.16
7.如图,半径为R的⊙O的弦AC=BD.且AC⊥BD于E,连接AB,AD,若AD=2,则半径R的长为( )
A.1 B. C.2 D.2
8.如图,A,B在半径为的⊙O上,将沿着弦AB翻折,若∠AOB=150°,则图中月牙(阴影)的面积等于( )
A.π﹣3 B.π+3 C.2π﹣3 D.π
9.以下命题:①直径是弦; ②长度相等的弧是等弧; ③相等的弦所对的弧也相等; ④圆的对称轴是直径;其中正确的个数是( )
A.4 B.3 C.2 D.1
10.如图,四边形ABCD内接于半圆O,AB为直径,AB=4,AD=DC=1,则弦BC的长为( )
A.3.5 B.2 C. D.
11.如图:AB为半圆的直径,AB=4,C为OA中点,D为半圆上一点,连CD,E为的中点,且CD∥BE,则CD的长为( )
A. B. C. D.
12.如图,OA,OB,OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC.则下列结论正确的是( )
A.AB=2BC B.AB<2BC C.∠AOB=2∠CAB D.∠ACB=4∠CAB
13.如图,四边形ABCD中,连接AC、BD,点O为AB的中点,若∠ADB=∠ACB=90°,则下面结论不一定正确的是( )
A.DC=CB
B.∠DAC=∠DBC
C.∠BCD+∠BAD=180°
D.点A、C、D到点O的距离相等
14.将一个半径为1的圆形轮子沿直线l水平向右滚动,图中显示的是轮子上的点P的起始位置与终止位置,其中在起始位置时PO∥l,在终止位置时PO与l所夹锐角为60°,则滚动前后,圆心之间的距离可能为( )
A. B. C.π D.
15.如图,AB是⊙O的直径,M、N分别是AO,BO的中点,CM⊥AB,DN⊥AB,则的度数 .
16.如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=46°,=,则
∠DAB= °.
17.如图,已知AB、BC为⊙O的弦,AB=,BC=1,∠AOC=90°,则⊙O半径为 .
18.点A、C为直径是6的圆周上两点,点B为的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为 .
19.如图,多边形ABDEC是由边长为m的等边△ABC和正方形BDEC组成,⊙O过A、D、E三点,则∠ACO= .
20.如图,AB是⊙O的直径,弦CD与AB交于点E,的度数是72°,∠BCD=68°,则∠AED的度数为 .
21.如图,在扇形AOB中,∠AOB=60°,AO=6,点D为的中点,C为半径OA上一动点(点A除外),沿CD对折后点A恰好落在扇形AOB的边线OB或OA上,AC的长可以是 .
22.如图.点A、B把⊙O分成2:7两条弧,则∠AOB= .
23.已知圆O的半径长为6,若弦AB=6,则弦AB所对的圆心角等于 .
24.如图,△ABC内接于⊙O,AB=AC,点E,F分别在和上,若∠ABC=50°,则∠BEC= °,∠BFC= °.
25.如图,扇子的圆心角为α,余下扇形的圆心角为β,为了使扇子的外形美观,通常情况下α与β的比按黄金比例设计,若取黄金比为0.6,则α= 度.
26.如图,在⊙O中,若==,则AC与2CD的大小关系是:AC 2CD.(填“>”,“<”或“=”)
27.如图所示,四边形AB∥CD,AD=DC=DB=p,BC=q,则AC= (用p、q表示).
28.如图,已知⊙O的半径为30mm,弦AB=36mm,则sin∠OAB= .
29.如图,等腰△ABC的顶角∠A=40°,以AB为直径的半圆与BC、AC分别交于D、E两点,则∠EBC= ,的度数为 .
30.如下图,弦CD、FE的延长线交于圆外点P,割线PAB经过圆心,请你结合现有图形,添加一个适当的条件: ,使结论∠1=∠2能成立.
31.如图,在⊙O中,点C为劣弧AB的中点,连接AC并延长至D,使CA=CD,连接DB并延长交⊙O于点E,连接AE.若BE,BD的长度分别是方程x2﹣5x+6=0的两个解,则△AED中,DE边上的高的长度为 .
32.如图,在⊙O中,两弦AD∥BC,AC,BD相交于点E,连接AB,CD,图中的全等三角形共有 对.相似比不等于1的相似三角形共有 对.
33.如图,在⊙O中,=,∠A=30°,则∠B= °.
34.如图,以Rt△ABC的直角顶点为圆心,以BA为半径的圆分别交AC于点D,交BC于点E.若∠C=31°,求的度数.
35.如图,已知AB是半径为1的圆O的一条弦,且AB<1,以AB为一边在圆O内作正△ABC,点D为圆O上不同于点A的一点,且DB=AB,DC的延长线交圆O于点E,试探究AE的长是否为定值(不随AB长度的变化而变化)?若为定值,求出这个定值;若不为定值,试确定AE与OA长之间的关系. .
36.如图,AB、CD是⊙O的直径,弦CE∥AB,所对的圆心角为30°.求∠AOC的度数.
37.如图,MB,MD是⊙O的两条弦,点A,C分别在,上,且AB=CD,M是的中点.
(1)求证:MB=MD;
(2)过O作OE⊥MB于点E,当OE=1,MD=4时,求⊙O的半径.
38.如图,在⊙O中,弦AB与DC相交于E,且BE=DE,求证:=.
39.如图,A、B、C、D是⊙O上四点,且AB=CD,求证:AD=BC.
40.如图,A,B,C,D在⊙O上,若AC=BD,求证:BC=AD.
参考答案
1.解:连接AC,
∵CB=CD,AD=AB,
∴=,=,
∴=,
即AC是圆的直径,
∴∠D=∠B=90°,
∵圆的半径为2,
∴AC=4,
∵CB=CD=2,
由勾股定理得:AD=AB==2,
∴S四边形ABCD
=S△ADC+S△ABC
=+
=+
=4,
故选:A.
2.解:∵AB是圆O的直径,
∴∠ACB=90°.
而∠DPB=60°,
∴∠APC=60°.
∴∠CAD=30°.
又∵D是的中点,
∴∠CAD=∠BAD=30°.
∴∠ABC=180°﹣30°﹣30°﹣90°=30°.
∴=.
故选:A.
3.解:设正多边形的边数为n.
由题意=72°,
∴n=5,
故选:B.
4.解:弦所对的圆心角=劣弧所对的圆心角=×360°=72°.
故选:B.
5.解:∵OA=OB,∠OAB=25°,
∴∠OBA=∠OAB=25°,
∴∠AOB=180°﹣∠OAB﹣∠OBA=130°,
∵OA=OC,∠OCA=40°,
∴∠OAC=∠OCA=40°,
∴∠AOC=180°﹣∠OAC﹣∠OCA=100°,
∴∠BOC=∠AOB﹣∠AOC=130°﹣100°=30°,
故选:A.
6.解:如图,连接OF.
∵DE⊥AB,
∴DE=EF,=,
∵点D是弧AC的中点,
∴=,
∴=,
∴AC=DF=12,
∴EF=DF=6,设OA=OF=x,
在Rt△OEF中,则有x2=62+(x﹣3)2,
解得x=,
∴AB=2x=15,
故选:C.
7.解:连接OA,OD,
∵弦AC=BD,
∴=,
∴=,
∴∠ABD=∠BAC,
∴AE=BE,
∵AC⊥BD,AE=BE,
∴∠ABE=∠BAE=45°,
∴∠AOD=2∠ABE=90°,
∵OA=OD,
∴AD=R,
∵AD=2,
∴R=2,
故选:C.
8.解:如图,作BD⊥AO交AO于点D.
∵OA=OB,∠AOB=150°,
∴∠DOB=30°,
∵OB=,
∴BD=OB=,
S阴=S圆O﹣2 S弓形AmB=π ()2﹣2(﹣××)=6π﹣5π+3=π+3,
故选:B.
9.解:①直径是弦,是真命题;
②在同圆或等圆中,长度相等的弧是等弧,原命题是假命题;
③在同圆或等圆中,相等的弦所对的弧也相等,原命题是假命题;
④圆的对称轴是直径所在的直线,原命题是假命题;
故选:D.
10.解:如图,连AC、BD,过D作DE⊥AC于E.
∴∠ADB=∠ACB=90°,∠ABD=∠CAD.
∵BD==.
∵AD=DC=1,
∴∠DAC=∠DCA,
∵∠DCA=∠ABD,
cos∠CAD=cos∠ABD==.
∴AE=AD cos∠CAD=,
∴AC=2AE=,
∴BC==.
故选:A.
11.解:如图,连接EO并延长与DC的延长线相交于点K,连接BD交OE于点H,
∵E为弧AD中点,
∴OE⊥AD,BH=DH,
∵BE∥CD,
∴∠EBH=∠KDH,∠E=∠K,
∴△BHE≌△DHK(AAS),
∴BE=KD=2x,EH=KH,
∵BE∥CD,
∴△KCO∽△EBO,
∴,
∵AB是半圆⊙O的直径,AB=4,C为OA的中点,
∴,
∴KO=1,KC=x,
∴KE=KO+OE=1+2=3,
∴EH=KH=1.5,OH=0.5,
∵BE2﹣EH2=BH2=BO2﹣OH2,
∴4x2﹣1.52=22﹣0.52,
解得:x=,
∴CD=KD﹣KC=2x﹣x=x=,
故选:B.
12.解:取的中点D,连接AD,BD,
∵∠AOB=2∠BOC,
∴=2,
∴==,
∴AD=BD=BC,
∵AB<AD+BD,
∴AB<2BC.故A错误,B正确;
∵∠AOB=2∠BOC,∠BOC=2∠CAB,
∴∠AOB=4∠CAB;故C错误;
∵∠AOB=2∠ACB,
∴∠ACB=∠BOC=2∠CAB,故D错误.
故选:B.
13.解:∵点O为AB的中点,∠ADB=∠ACB=90°,
∴D,C在以O为圆心,AB为直径的圆上,如图,
∴∠DAC=∠DBC,∠BCD+∠BAD=180°,点A、C、D到点O的距离相等,
当∠DAC=∠BAC时,DC=CB,而题目中未给出.
故选:A.
14.解:由题意可得,圆形轮子可能滚动不止一周,设OP滚动了n周后又滚动120°后到达终止位置,
∴OP滚动的角度α=120°+360n,n为整数,
可得圆心运动前后的距离即为OP滚动完毕扫过的角度所对应的弧长,
即为2πr×=,n为整数.
当n=0时为.
故选:B.
15.解:∵AB是⊙O的直径,M、N分别是AO,BO的中点,
∴2OM=OC,2ON=OD,
∵CM⊥AB,DN⊥AB,
∴∠CMO=∠DNO=90°,
∴∠MCO=∠NDO=30°,
∴∠MOC=∠NOD=60°,
∴∠COD=180°﹣60°﹣60°=60°,
∴的度数是60°,
故答案为:60°
16.解:∵AB是半圆O的直径,
∴∠ACB=90°,
∵∠BAC=46°,
∴∠B=44°.
∴∠ADC=180°﹣44°=136°.
∵=,
∴AD=DC.
∴∠DAC=∠DCA==22°,
∴∠BAD=∠DAC+∠BAC=22°+46°=68°.
故答案是:68.
17.解:作AH⊥CB交CB的延长线于H,连接AC.
由∠AOC=90°,可得∠ABC=135°,
在Rt△AHB中,∵AB=,∠ABH=45°,
∴AH=BH=1,
在Rt△AHC中,∵CH=CB+BH=2,AH=1,
∴AC==,
∵OA=OC,∠AOC=90°,
∴OA=OC=,
故答案为.
18.解:过B作直径,连接AC交AO于E,
∵点B为的中点,
∴BD⊥AC,
如图①,
∵点D恰在该圆直径的三等分点上,
∴BD=×6=2,
∴OD=OB﹣BD=,
∵四边形ABCD是菱形,
∴DE=BD=,
∴OE=2,
连接OC,
∵CE=,
∴边CD=;
如图②,BD=×6=4,
同理可得,OD=,OE=,DE=2,
连接OC,
∵CE=,
∴边CD=,
故答案为6或3.
19.解:∵多边形ABDEC是由边长为m的等边△ABC和正方形BDEC组成,
∴AC=EC,∠ACE=∠ACB+∠ECB=60°+90°=150°,
∵⊙O过A,D,E三点,
∴AO=EO,
又OC=OC,
∴△ACO≌ECO(SSS),
∴∠ACO=∠ECO=∠ACE=1/2×150°=75°,
故答案为:75°.
20.解:∵AB是⊙O的直径,的度数是72°,
∴=180°﹣72°=108°,
∴∠ABC==×108°=54°,
∵∠BCD=68°,
∴∠CEB=180°﹣∠BCD﹣∠ABC=180°﹣68°﹣54°=58°.
故答案为:58°.
21.解:①当点E落在半径OA上时,连接OD,如图1所示,
∵∠ACD=90°,∠AOB=60°,点D为弧AB的中点,点A(2,0),
∴∠COD=30°,OA=OD=6,
∴OC=OD cos30°=6×=3,
∴AC=OA﹣OC=6﹣3;
②如图2,沿CD对折后点A恰好落在边线OB上,且A′和B重合时,
则C和O重合,此时,AC=OA=6;
③沿CD对折后点A恰好落在边线OB上,且A′和B不重合时,如图3;
连接OD、BD、AD,作DF⊥OA于F,
∵∠AFD=90°,∠AOB=60°,点D为弧AB的中点,
∴∠AOD=∠BOD=30°,∠OAD=∠OBD,
∵OA=OD=6,
∴DF=OD sin30°=6×=3,∠OAD=75°,
∴OF=OD cos30°=6×=3,
∴AF=OA﹣OD=6﹣3,
∵DA′=DA=DB,∠OAD=∠OBD=75°,
∴BA′=2AF=12﹣6,∠DA′B=∠OBD=75°,
∴OA′=OB﹣BA′=6﹣(12﹣6)=6﹣6,
∵∠CA′D=∠CAD=75°,
∴∠BA′C=150°,
∴∠OA′C=30°,
∴∠A′CO=90°,
∴CA′=OA′ sin60°=(6﹣6)×=9﹣3,
∴AC=CA′=9﹣3.
故答案为:6﹣3或6或9﹣3.
22.解:∠AOB的度数=×360°=80°.
故答案为80°.
23.解:如图,作OC⊥AB于C,连接OA、OB,
则AC=BC=AB=3,
在Rt△AOC中,OC==3,
∴OC=OA,
∴∠A=30°,
∴∠AOB=180°﹣30°﹣30°=120°.
∴弦AB所对的圆心角的度数为120°.
故答案为120°.
24.解:∵∠ABC=50°,AB=AC,∴∠ABC=∠ACB=50°,
∴∠A=80°,∴∠BEC=80°,
∴∠F=180°﹣80°=100°.
故答案为:80°;100°.
25.解:∵∠α+∠β=360°,且∠α:∠β=0.6,
∴∠β=360°÷1.6=225°,∠α=360°﹣225°=135°.
故本题答案为:135°.
26.解:如图,连接AB、BC,
在⊙O中,若==,
∴AB=BC=CD,
在△ABC中,AB+BC>AC.
∴AC<2CD.
故答案是:<.
27.解:延长CD交半径为p的⊙D于E点,连接AE.显然A、B、C在⊙D上.
∵AB∥CD
∴=,
∴BC=AE=q.
在△ACE中,∠CAE=90°,CE=2p,AE=q,
故AC==.
故答案为:.
28.解:过O作OC⊥AB于C,
∵OC⊥AB,OC过O,AB=36cm,
∴AC=BC=AB=18cm,
在Rt△OCA中,由勾股定理得:OA2=OC2+AC2,
302=OC2+182,
OC=24(cm),负数舍去;
所以sin∠OAB===,
故答案为:.
29.解:连AD,如图,
∵AB为直径,
∴∠ADB=90°,即AD⊥BC,
又∵AB=AC,
∴AD平分∠BAC,
而∠A=40°,
∴∠BAD=∠DAC=20°,
∴∠EBC=∠DAC=20°,
∴弧BD的度数=弧DE的度数=2×20°=40°,
∴弧AE的度数=180°﹣40°﹣40°=100°.
故答案为20°,100°.
30.解:使∠1=∠2能成立,则应有△COP≌△EOP,或△PDB≌△PFB,故可添加AC=AE或BD=BF当AC=AE时,
根据圆周角定理知,∠AOC=∠AOE,∵OC=OE,PO=PO,∴△COP≌△EOP,∴∠1=∠2.
31.解:如图,连接AB,EC.
∵AB是直径,
∴∠ABE=∠ACE=90°,
即EC⊥AD,AB⊥DE,
∵AC=CD,
∴EA=ED,
∵BE,BD的长度分别是方程x2﹣5x+6=0的两个解,
∴BE=2,BD=3或BE=3,BD=2,
当BE=2,BD=3时,EA=BD=5,
∴AB===,
当BE=2,BD=3时,EA=BD=5,
∴AB===4,
综上所述,或4.
32.解:由题意可得全等三角形共有三对,分别为:△ABE≌△DCE、△ABD≌△DCA、△ABC≌△DCB
相似三角形有一对,为△ADE∽△CBE.
33.解:∵在⊙O中,=,
∴AB=AC,
∴△ABC是等腰三角形,
∴∠B=∠C;
又∠A=30°,
∴∠B==75°(三角形内角和定理).
故答案是:75.
34.解:连接BD.
在Rt△ABC中,∵∠ABC=90°,∠C=31°,
∴∠A=90°﹣31°=59°,
∵BA=BD,
∴∠A=∠ADB=59°,
∴∠ABD=180°﹣∠A﹣∠ADB=180°﹣2×59°=62°,
∴∠DBE=90°﹣∠ABD=90°﹣62°=28°,
∴的度数为28°.
35.解:由A、B、D、E四点共圆,
∴∠EAB+∠EDB=180°,
∵BC=BD,∠BDC=∠BCD,∠BCD+∠ECB=180°,
∴∠ECB=∠EAB
又∵∠CAB=∠ACB=60°
∴∠ECB﹣∠ACB=∠EAB﹣∠CAB,
∴∠ECA=∠EAC,
∴△EAC是等腰三角形,
∵AB=BD,
∴∠DEA=∠DOB,
∵AC=AB,
∴△EAC≌△OAB,
∴AE=OA=1.
36.解:连接OE,如图,
∵为30°,
∴∠COE=30°,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OCE=(180°﹣30°)÷2=75°,
∵弦CE∥AB,
∴∠AOC=∠OCE=75°.
37.(1)证明:∵AB=CD,
∴=,
∵M是的中点,
∴=,
∴=,
∴BM=DM.
(2)解:如图,连接OM.
∵DM=BM=4,OE⊥BM,
∴EM=BE=2,
∵OE=1,∠OEM=90°,
∴OM===,
∴⊙O的半径为.
38.证明:在△AED和△CEB中,
,
∴△AED≌△CEB(AAS).
∴AD=BC,
∴=.
39.证明:∵AB=CD,
∴=,
∴+=+,
∴=,
∴AD=BC.
40.证明:∵AC=BD,
∴=.
∴﹣=﹣.即=.
∴BC=AD.
