鲁教版(五四制)2021-2022学年九年级数学下册5.5确定圆的条件 同步练习题 (word版、含解析)
文档属性
| 名称 | 鲁教版(五四制)2021-2022学年九年级数学下册5.5确定圆的条件 同步练习题 (word版、含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 483.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 16:23:06 | ||
图片预览



文档简介
2021-2022学年鲁教版九年级数学下册《5.5确定圆的条件》同步练习题(附答案)
1.如图,AB是半⊙O的直径,点C在半⊙O上,AB=5cm,AC=4cm.D是上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE.在点D移动的过程中,BE的最小值为( )
A.1 B.﹣2 C.2﹣1 D.3
2.下列说法错误的是( )
A.已知圆心和半径可以作一个圆
B.经过一个已知点A的圆能作无数个
C.经过两个已知点A,B的圆能作两个
D.经过不在同一直线上的三个点A,B,C只能作一个圆
3.如图,△ABC内接于⊙O,D是BC的中点,连接OD并延长交⊙O于点E,连接EC,若∠OEC=65°,则∠A的大小是( )
A.50° B.55° C.60° D.65°
4.⊙O的半径为5cm,点P到圆心O的距离为7cm,则点P与⊙O的位置关系是( )
A.在圆上 B.在圆内 C.在圆外 D.不确定
5.已知⊙O的直径为4cm,点P到圆心O的距离OP=3cm,则点P( )
A.在⊙O外 B.在⊙O上 C.在⊙O内 D.不能确定
6.数轴上有两个点A和B,点B表示实数6,点A表示实数a,⊙B半径为4.若点A在⊙B内,则( )
A.a<2或a>10 B.2<a<10 C.a>2 D.a<10
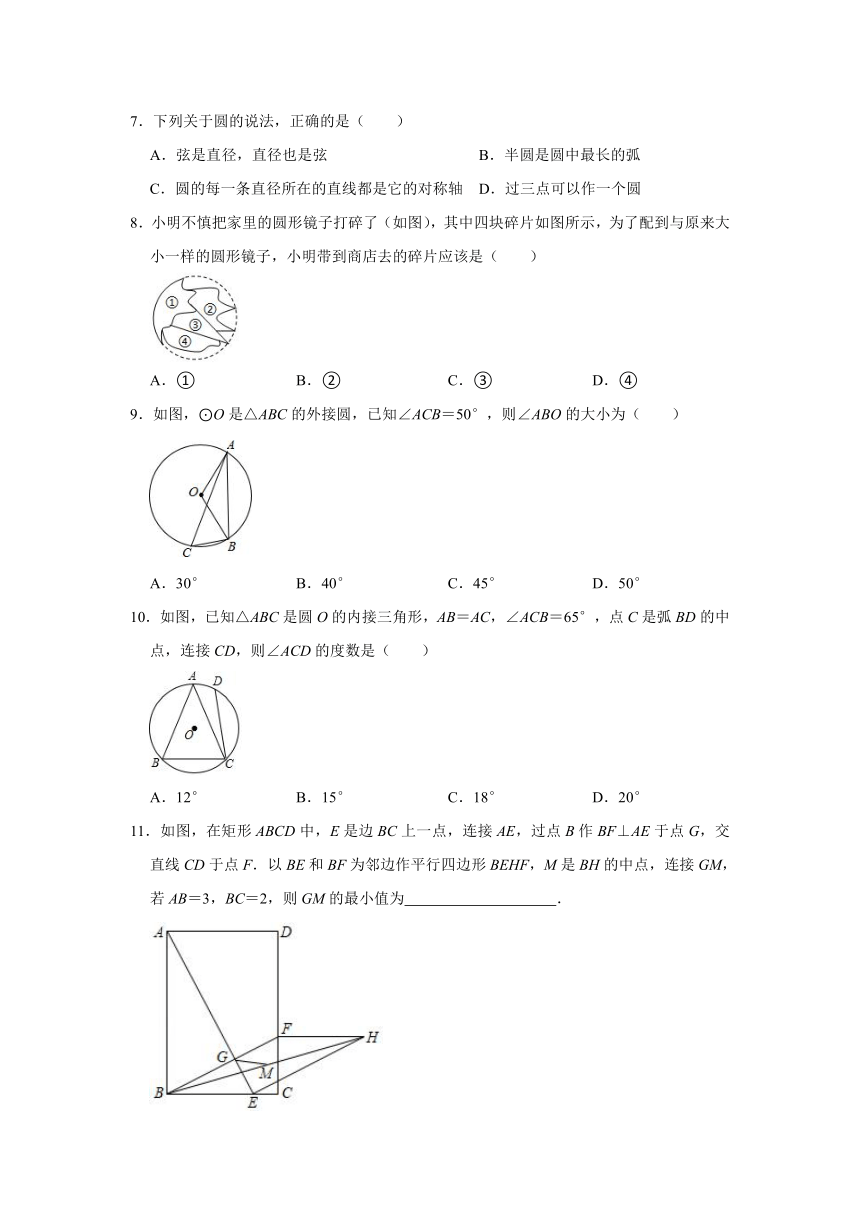
7.下列关于圆的说法,正确的是( )
A.弦是直径,直径也是弦 B.半圆是圆中最长的弧
C.圆的每一条直径所在的直线都是它的对称轴 D.过三点可以作一个圆
8.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是( )
A.① B.② C.③ D.④
9.如图,⊙O是△ABC的外接圆,已知∠ACB=50°,则∠ABO的大小为( )
A.30° B.40° C.45° D.50°
10.如图,已知△ABC是圆O的内接三角形,AB=AC,∠ACB=65°,点C是弧BD的中点,连接CD,则∠ACD的度数是( )
A.12° B.15° C.18° D.20°
11.如图,在矩形ABCD中,E是边BC上一点,连接AE,过点B作BF⊥AE于点G,交直线CD于点F.以BE和BF为邻边作平行四边形BEHF,M是BH的中点,连接GM,若AB=3,BC=2,则GM的最小值为 .
12.已知直线l:y=x﹣4,点A(1,0),点B(0,2),设点P为直线l上一动点,当点P的坐标为 时,过P、A、B不能作出一个圆.
13.锐角△ABC,其外接圆圆心为O,AB、AC上的高交于H,若O、H、B、C在同一圆周上,则∠BAC= .
14.已知⊙O的半径为1,点P与点O之间的距离为d,且关于x的方程x2﹣2x+d=0没有实数根,则点P在 (填“圆内”“圆上”或“圆外”).
15.如图,在边长为2的正方形ABCD中,点E,F分别是边AD,CD上的动点,且AE=DF,连接BE,AF,线段BE和AF相交于点G,连接CG,取CG的中点H,连接DH,则线段DH的最小值为 .
16.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3,点D是AB的中点,点E是以点B为圆心,BD长为半径的圆上的一动点,连接AE,点F为AE的中点,则CF长度的最大值是 .
17.在平面直角坐标系中有A,B,C三点,A(1,3),B(3,3),C(5,1).现在要画一个圆同时经过这三点,则圆心坐标为 .
18.如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是 .
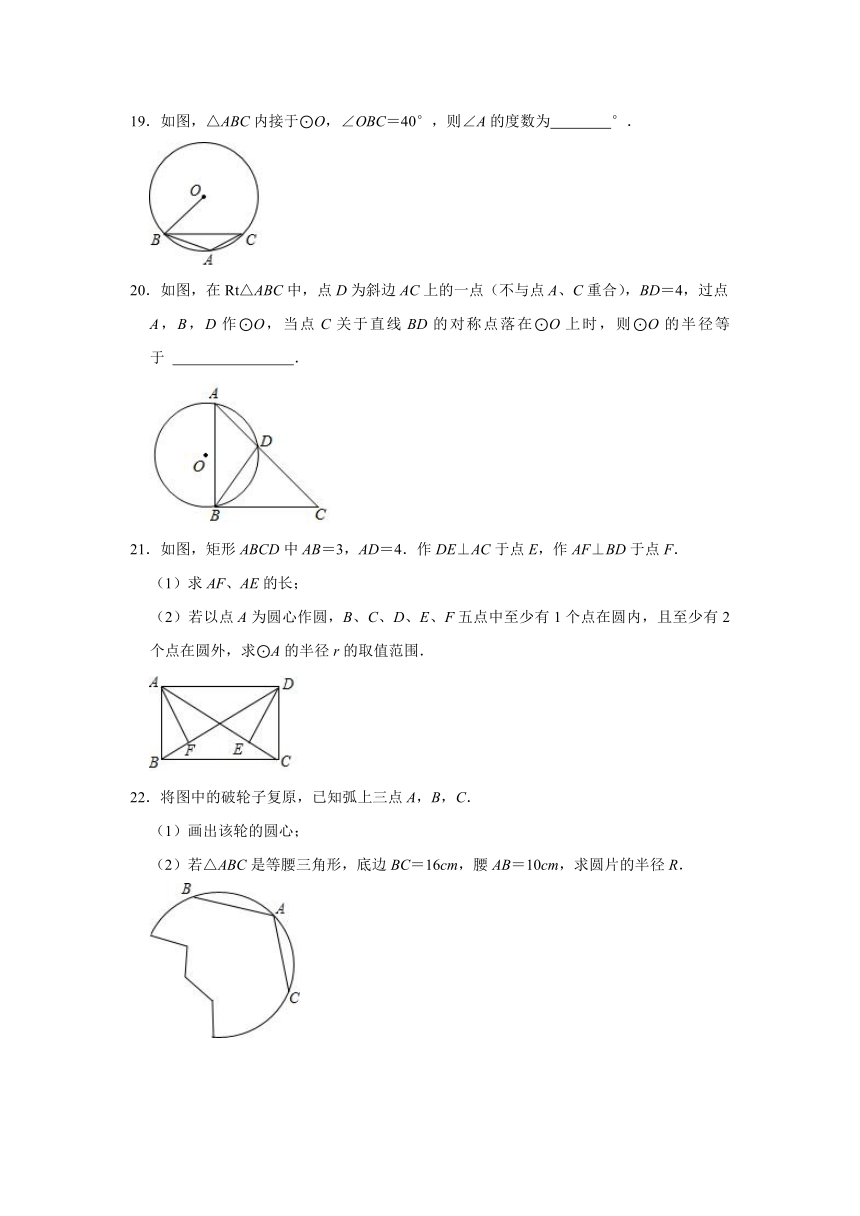
19.如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为 °.
20.如图,在Rt△ABC中,点D为斜边AC上的一点(不与点A、C重合),BD=4,过点A,B,D作⊙O,当点C关于直线BD的对称点落在⊙O上时,则⊙O的半径等于 .
21.如图,矩形ABCD中AB=3,AD=4.作DE⊥AC于点E,作AF⊥BD于点F.
(1)求AF、AE的长;
(2)若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求⊙A的半径r的取值范围.
22.将图中的破轮子复原,已知弧上三点A,B,C.
(1)画出该轮的圆心;
(2)若△ABC是等腰三角形,底边BC=16cm,腰AB=10cm,求圆片的半径R.
23.如图,在四边形ABCD中,AB=AC,∠ADB=90°,过A,B,D三点的圆交BC边于点E.
(1)求证:E是BC的中点;
(2)若BC=2CD,求证:∠BCD=2∠ABD.
24.如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动,设运动时间为t秒.
(1)当t=2时,△DPQ的面积为 cm2;
(2)运动过程中,当A、P、Q、D四点恰好在同一个圆上时,求t的值.
25.阅读下列材料:
平面上两点P1(x1,y1),P2(x2,y2)之间的距离表示为|P1P2|=,称为平面内两点间的距离公式,根据该公式,如图,设P(x,y)是圆心坐标为C(a,b)、半径为r的圆上任意一点,则点P适合的条件可表示为=r,变形可得:(x﹣a)2+(y﹣b)2=r2,我们称其为圆心为C(a,b),半径为r的圆的标准方程.
例如:由圆的标准方程(x﹣1)2+(y﹣2)2=25可得它的圆心为(1,2),半径为5.根据上述材料,结合你所学的知识,完成下列各题.
(1)圆心为C(3,4),半径为2的圆的标准方程为: ;
(2)若已知⊙O的标准方程为:(x﹣2)2+y2=22,圆心为C,请判断点A(3,﹣1)与⊙O的位置关系.
26.如图,平面直角坐标系xOy中,矩形OABC如图放置,点B(4,3),E,F分别为OA,BC边上的中点,动点P从点E出发以每秒2个单位速度沿EO方向向点O运动,同时,动点Q从点F出发以每秒1个单位速度沿FB方向向点B运动.当一个点到达终点时,另一个点随之停止.连接EF、PQ,且EF与PQ相交于点M,连接AM.
(1)求线段AM的长度;
(2)过点A作AH⊥PQ,垂足为点H,连接CH,求线段CH长度的最小值.
27.如图所示,BD,CE是△ABC的高,求证:E,B,C,D四点在同一个圆上.
28.已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点B.C.D.E在以点M为圆心的同一个圆上.
29.如图,⊙O是△ABC的外接圆,∠AOB=96°,∠CAB=60°,点D是的中点.求∠ABD的度数.
30.如图,⊙O为△ABC的外接圆,AB为⊙O直径,AC=BC,点D在劣弧BC上,CE⊥CD交AD于E,连接BD.
(1)求证:△ACE≌△BCD.
(2)若CD=2,BD=3,求⊙O的半径.
(3)若点F为DE的中点,连接CF,FO,设CD=a,BD=b,求CF+FO.(用含有a,b的代数式表示)
参考答案
1.解:如图,连接BO′、BC.
∵CE⊥AD,
∴∠AEC=90°,
∴在点D移动的过程中,点E在以AC为直径的圆上运动,
∵AB是直径,
∴∠ACB=90°,
在Rt△ABC中,∵AC=4,AB=5,
∴BC===3,O′E=2,
在Rt△BCO′中,BO′===,
∵O′E+BE≥O′B,
∴当O′、E、B共线时,BE的值最小,最小值为O′B﹣O′E=﹣2,
故选:B.
2.解:A、已知圆心和半径可以作一个圆,说法正确,故不符合题意.
B、只有确定圆心和半径才能确定一个圆,所以经过一个已知点A的圆能作无数个,说法正确,故不符合题意.
C、只有确定圆心和半径才能确定一个圆,所以已知点A,B的圆能作无数个,说法错误,故符合题意.
D、经过不在同一直线上的三个点A,B,C只能作一个圆,说法正确,故不符合题意.
故选:C.
3.解:∵∠OEC=65°,OE=OC,
∴∠EOC=180°﹣2×65°=50°,
∵D是BC的中点,
∴OE⊥BC,
∴,
∴∠EOB=50°,
∴∠BOC=100°,
∴∠A=50°,
故选:A.
4.解:∵⊙O的半径为5cm,点P到圆心O的距离为7cm,
∴OP>⊙O的半径,
∴点P在⊙O外.
故选:C.
5.解:∵⊙O的直径为4cm,
∴半径为2cm,
∵点P到圆心O的距离OP=3cm>2cm,
∴点P在⊙O外.
故选:A.
6.解:∵点B表示实数6,⊙B半径为4.
∴数轴与⊙B的交点表示的数为2或10,
∵点A表示实数a,点A在⊙B内,
∴2<a<10,
故选:B.
7.解:A、弦不一定是直径,但直径是弦,本选项说法错误,不符合题意;
B、∵半圆小于优弧,
∴半圆是圆中最长的弧说法错误,本选项不符合题意;
C、圆的每一条直径所在的直线都是它的对称轴,本选项说法正确,符合题意;
D、过不在同一直线上的三点可以作一个圆,本选项说法错误,不符合题意;
故选:C.
8.解:第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
9.解:∵∠ACB=50°,
∴∠AOB=100°,
∵AO=BO,
∴∠ABO=(180°﹣100°)÷2=40°,
故选:B.
10.解:如图,连接AO,BO,CO,DO,
∵AB=AC,∠ACB=65°,
∴∠ABC=∠ACB=65°,
∴∠BAC=50°,
∴∠AOC=2∠ABC=130°,∠BOC=2∠BAC=100°,
∵点C是弧BD的中点,
∴,
∴∠BOC=∠COD=100°,
∴∠AOD=30°,
∵∠AOC=2∠ACD,
∴∠ACD=15°,
故选:B.
11.解:∵四边形BEHF是平行四边形,
∴EM=FM,
∵∠EGF=90°,
∴GM=EF,
∴要GM最小,即EF最小,
∵AB=3,BC=2,
设BE=x,则CE=2﹣x,
∵四边形ABCD为矩形,
∴∠ABC=90°,即∠BAE+∠AEB=90°,
∵AE⊥BF,
∴∠CBF+∠AEB=90°,
∴∠CBF=∠BAE,
又∵∠ABE=∠BCF=90°,
∴△ABE∽△BCF,
∴,即=,
∴CF=,
∴EF===,
设y=x2﹣4x+4,
当x=时,y取最小值,
∴EF的最小值为,
故GM的最小值为.
故答案为.
12.解:设直线AB的解析式为y=kx+b,
∵A(1,0),点B(0,2),
∴,
解得,
∴y=﹣2x+2.
解方程组,得,
∴当P的坐标为(2,﹣2)时,过P,A,B三点不能作出一个圆.
故答案为(2,﹣2)
13.解:如图,连接OB,OC,
∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°,
∴∠BAC+∠DHE=360°﹣∠ADC﹣∠AEB=180°,
∵O、H、B、C在同一圆周上,
∴∠BOC=∠BHC=∠DHE,
∴∠BAC+∠BOC=180°,
∵∠BOC=2∠BAC,
∴∠BAC+∠BOC=3∠BAC=180°,
∴∠BAC=60°,
故答案为:60°.
14.解:∵方程x2﹣2x+d=0没有实数根,
∴Δ=b2﹣4ac=4﹣4d<0,
∴d>1,
∵⊙O的半径为1,
∴d>r;
∴点P在⊙O的外部,
故答案为:圆外.
15.
解:以AD所在的直线为对称轴,作正方形ABCD的对称正方形ANMD,
∴MD=CD,MN=AD=2,∠N=90o,
∵H为GC的中点,
∴HD为△GMC的中位线,
∴DH=GM,
∴当GM最短时,DH最短,
∵四边形ABCD是正方形,
∴BA=AD,∠BAE=∠ADF=90°,
∵AE=DF,
∴△ABE≌△DAF,
∴∠ABE=∠DAF,
∵∠BAD=∠BAG+∠DAF=90°,
∴∠ABE+∠DAF=90°,
∴∠ABE+∠BAG=90°,
∴∠AGB=90°,
∴点G在以AB为直径的圆O上,
∴当点G在OM上时,GM最短,
∴OM=,
∴GM=OM﹣OG=﹣1,
∴DH=GM=,
故答案为:.
16.解:如图,延长AC到T,使得CT=AC,连接BT,TE,BE.
∵AC=CT,BC⊥AT,
∴BA=BT,
∵∠ACB=90°,∠ABC=30°,BC=3,
∴∠BAT=60°,AC=BC tan30°=3,
∴AB=2AC=6,
∴△ABT是等边三角形,
∴BT=AB=6,
∵AD=BD=BE,
∴BE=3,
∵ET≤BT+BE,
∴ET≤9,
∴ET的最大值为9,
∵AC=CT,AF=FE,
∴CF=ET,
∴CF的最大值为.
故答案为:.
17.解:∵A(1,3),B(3,3),C(5,1)不在同一直线上
∴经过点A,B,C可以确定一个圆
∴该圆圆心必在线段AB的垂直平分线上
∴设圆心坐标为M(2,m)
则点M在线段BC的垂直平分线上
∴MB=MC
由勾股定理得:=
∴1+m2﹣6m+9=9+m2﹣2m+1
∴m=0
∴圆心坐标为M(2,0)
故答案为:(2,0).
18.解:根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,1).
故答案为:(2,1).
19.解:连接OC,如图所示,
∵OB=OC,
∴∠OCB=∠OBC=40°,
∴∠BOC=100°,
∵∠1+∠BOC=360°,
∴∠1=260°,
∵∠A=∠1,
∴∠A=130°.
故答案为:130.
20.解:作点C的对称点C′,连接C′D,OB,OD.
∴∠BC'D=∠BAD,
由折叠的性质,可知∠BC'D=∠BCD,
∴∠BAC=∠ACB,
∵∠ABC=90°,
∴△ABC是等腰直角三角形,
∴∠BD′C=∠BCD=∠BAD=45°,
∴∠BOD=90°,
∴半径=2.
故答案为:2.
21.解:(1)∵矩形ABCD中AB=3,AD=4,
∴AC=BD==5,
∵AF BD=AB AD,
∴AF==,
同理可得DE=,
在Rt△ADE中,AE==;
(2)∵AF<AB<AE<AD<AC,
∴若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,即点F在圆内,点D、C在圆外,
∴⊙A的半径r的取值范围为2.4<r<4.
22.解:(1)如图所示:分别作弦AB和AC的垂直平分线交点O即为所求的圆心;
(2)连接AO,OB,BC,BC交OA于D.
∵BC=16cm,
∴BD=8cm,
∵AB=10cm,
∴AD=6cm,
设圆片的半径为R,在Rt△BOD中,OD=(R﹣6)cm,
∴R2=82+(R﹣6)2,
解得:R=cm,
∴圆片的半径R为cm.
23.证明:(1)连接AE,如图,
∵∠ADB=90°,
∴AB为直径,
∴∠AEB=90°,
∴AE⊥BC,
∵AB=AC,
∴AE是△ABC的中线,
∴E是BC的中点,
(2)连接DE,如图,
∵E是BC的中点,
∴BC=2CE,
∵BC=2CD,
∴CE=CD,
∴∠CDE=∠CED,
∵四边形ADEB是圆的内接四边形,
∴∠BAD+∠BED=180°.
∵∠CED+∠BED=180°,
∴∠BAD=∠CED,
∵∠ABD=90°﹣∠BAD,∠BCD=180°﹣∠CED﹣∠CDE=180°﹣2∠BAD,
∴∠BCD=2∠ABD.
24.解:(1)∵四边形ABCD是矩形,
∴AD=BC=12cm,CD=AB=6cm,∠A=∠B=∠C=90°,
由题意得:AP=tcm,BQ=2tcm,
∴BP=AB﹣AP=(6﹣t)cm,CQ=BC﹣BQ=(12﹣2t)cm,
当t=2时,AP=2cm,BQ=4cm,BP=AB﹣AP=4cm,CQ=BC﹣BQ=8cm,
∴△DPQ的面积=12×6﹣×12×2﹣×4×4﹣×6×8=28(cm2),
故答案为:28;
(2)∵∠A=90°,
∴A、P、D三点在以DP为直径的圆上,
若点Q也在圆上,则∠PQD=90°,
∵PQ2=(6﹣t)2+(2t)2,DQ2=62+(12﹣2t)2,DP2=t2+122,PQ2+DQ2=DP2,
∴(6﹣t)2+(2t)2+62+(12﹣2t)2=t2+122;
解得t1=6,t2=,
∴当t=6或时A、P、Q、D四点恰好在同一个圆上.
25.解:(1)圆心为C(3,4),半径为2的圆的标准方程为:(x﹣3)2+(y﹣4)2=4.
故答案为:(x﹣3)2+(y﹣4)2=4.
(2)由题意圆心为C(2,0),
∵A(3,﹣1),
∴AC==<2,
∴点A在⊙C内部.
26.解:(1)设运动时间为t秒.则FQ=t,PE=2t.
∵B(4,3),四边形ABCO是矩形,
∴BC=OA=4,AB=OC=3,
∵CF=FB.OE=EA,
∴EF=OC=3,
∵FQ∥PE,
∴==,
∴FM=1.ME=2,
在Rt△AME中,∠AEM=90°,AE=EM=2,
∴AM=2.
(2)由题意,点H在以AM为直径的⊙T的圆上运动,连接CT,CH,TH.
∵A(4,0),M(2,2),MT=AT,
∴T(3,1),
∵C(0,3),
∴CT==,
∵TH=TM=TA=,
∴CH≥CT﹣TH,
∴CH≥﹣,
∴CH的最小值为﹣.
27.证明:如图所示,取BC的中点F,连接DF,EF.
∵BD,CE是△ABC的高,
∴△BCD和△BCE都是直角三角形.
∴DF,EF分别为Rt△BCD和Rt△BCE斜边上的中线,
∴DF=EF=BF=CF.
∴E,B,C,D四点在以F点为圆心,BC为半径的圆上.
28.证明:连接ME、MD,
∵BD、CE分别是△ABC的高,M为BC的中点,
∴ME=MD=MC=MB=BC,
∴点B、C、D、E在以点M为圆心的同一圆上.
29.解:∵∠AOB=96°,
∴∠C=AOB=48°,
∵∠CAB=60°,
∴∠ABC=180°﹣∠C﹣∠CAB=72°,
连接CD,
∴∠D=180°﹣∠CAB=120°,
∵点D是的中点,
∴=,
∴BD=CD,
∴∠CBD=×(180°﹣120°)=30°,
∴∠ABD=∠ABC+∠CBD=72°+30°=102°.
30.解:(1)证明:∵AB为⊙O直径,
∴∠ACB=90°,
∵CE⊥CD,
∴∠ECD=90°,
∴∠ACE=90°﹣∠ECB=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(ASA);
(2)∵△ACE≌△BCD,
∴CE=CD,AE=BD,
∵CE⊥CD,
∴△ECD是等腰直角三角形,
∵CD=2,BD=3,
∴DE=2,AE=3,
∴AD=5,
∵AB为⊙O直径,
∴∠ADB=90°,
∴AB==2,
∴⊙O的半径为;
(3)法一:过O作OH⊥AD于H,如图:
∵△ECD是等腰直角三角形,CD=a,
∴ED=a,
∵F为DE的中点,
∴CF=DF=DE=a,
∵△ACE≌△BCD,
∴AE=BD=b,
∴AD=ED+AE=a+b,
∵OH⊥AD,∠ADB=90°,
∴OH∥BD,
∵AO=OB,
∴DH=AD=a+b,OH=BD=b,
∴HF=DH﹣DF=(a+b)﹣a=b,
在Rt△OHF中,FO==b,
∴CF+FO=a+b.
法二:延长AD至点H,使DH=AE,连接BH,如图:
由(1)得△ACE≌△BCD,
∴BD=AE=DH,
∵AB为直径,
∴∠ADB=∠BDH=90°,
∴△BDH为等腰直角三角形,
∵BD=b,
∴BH=b,
∵△ECD是等腰直角三角形,CD=a,
∴ED=a,CF=a=DF=EF,
而DH=AE,
∴AE+EF=DH+DF,即AF=HF,
∴F为AH中点,
∵O为AB中点,
∴FO=BD=b,
∴CF+FO=a+b.
1.如图,AB是半⊙O的直径,点C在半⊙O上,AB=5cm,AC=4cm.D是上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE.在点D移动的过程中,BE的最小值为( )
A.1 B.﹣2 C.2﹣1 D.3
2.下列说法错误的是( )
A.已知圆心和半径可以作一个圆
B.经过一个已知点A的圆能作无数个
C.经过两个已知点A,B的圆能作两个
D.经过不在同一直线上的三个点A,B,C只能作一个圆
3.如图,△ABC内接于⊙O,D是BC的中点,连接OD并延长交⊙O于点E,连接EC,若∠OEC=65°,则∠A的大小是( )
A.50° B.55° C.60° D.65°
4.⊙O的半径为5cm,点P到圆心O的距离为7cm,则点P与⊙O的位置关系是( )
A.在圆上 B.在圆内 C.在圆外 D.不确定
5.已知⊙O的直径为4cm,点P到圆心O的距离OP=3cm,则点P( )
A.在⊙O外 B.在⊙O上 C.在⊙O内 D.不能确定
6.数轴上有两个点A和B,点B表示实数6,点A表示实数a,⊙B半径为4.若点A在⊙B内,则( )
A.a<2或a>10 B.2<a<10 C.a>2 D.a<10
7.下列关于圆的说法,正确的是( )
A.弦是直径,直径也是弦 B.半圆是圆中最长的弧
C.圆的每一条直径所在的直线都是它的对称轴 D.过三点可以作一个圆
8.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是( )
A.① B.② C.③ D.④
9.如图,⊙O是△ABC的外接圆,已知∠ACB=50°,则∠ABO的大小为( )
A.30° B.40° C.45° D.50°
10.如图,已知△ABC是圆O的内接三角形,AB=AC,∠ACB=65°,点C是弧BD的中点,连接CD,则∠ACD的度数是( )
A.12° B.15° C.18° D.20°
11.如图,在矩形ABCD中,E是边BC上一点,连接AE,过点B作BF⊥AE于点G,交直线CD于点F.以BE和BF为邻边作平行四边形BEHF,M是BH的中点,连接GM,若AB=3,BC=2,则GM的最小值为 .
12.已知直线l:y=x﹣4,点A(1,0),点B(0,2),设点P为直线l上一动点,当点P的坐标为 时,过P、A、B不能作出一个圆.
13.锐角△ABC,其外接圆圆心为O,AB、AC上的高交于H,若O、H、B、C在同一圆周上,则∠BAC= .
14.已知⊙O的半径为1,点P与点O之间的距离为d,且关于x的方程x2﹣2x+d=0没有实数根,则点P在 (填“圆内”“圆上”或“圆外”).
15.如图,在边长为2的正方形ABCD中,点E,F分别是边AD,CD上的动点,且AE=DF,连接BE,AF,线段BE和AF相交于点G,连接CG,取CG的中点H,连接DH,则线段DH的最小值为 .
16.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3,点D是AB的中点,点E是以点B为圆心,BD长为半径的圆上的一动点,连接AE,点F为AE的中点,则CF长度的最大值是 .
17.在平面直角坐标系中有A,B,C三点,A(1,3),B(3,3),C(5,1).现在要画一个圆同时经过这三点,则圆心坐标为 .
18.如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是 .
19.如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为 °.
20.如图,在Rt△ABC中,点D为斜边AC上的一点(不与点A、C重合),BD=4,过点A,B,D作⊙O,当点C关于直线BD的对称点落在⊙O上时,则⊙O的半径等于 .
21.如图,矩形ABCD中AB=3,AD=4.作DE⊥AC于点E,作AF⊥BD于点F.
(1)求AF、AE的长;
(2)若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求⊙A的半径r的取值范围.
22.将图中的破轮子复原,已知弧上三点A,B,C.
(1)画出该轮的圆心;
(2)若△ABC是等腰三角形,底边BC=16cm,腰AB=10cm,求圆片的半径R.
23.如图,在四边形ABCD中,AB=AC,∠ADB=90°,过A,B,D三点的圆交BC边于点E.
(1)求证:E是BC的中点;
(2)若BC=2CD,求证:∠BCD=2∠ABD.
24.如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动,设运动时间为t秒.
(1)当t=2时,△DPQ的面积为 cm2;
(2)运动过程中,当A、P、Q、D四点恰好在同一个圆上时,求t的值.
25.阅读下列材料:
平面上两点P1(x1,y1),P2(x2,y2)之间的距离表示为|P1P2|=,称为平面内两点间的距离公式,根据该公式,如图,设P(x,y)是圆心坐标为C(a,b)、半径为r的圆上任意一点,则点P适合的条件可表示为=r,变形可得:(x﹣a)2+(y﹣b)2=r2,我们称其为圆心为C(a,b),半径为r的圆的标准方程.
例如:由圆的标准方程(x﹣1)2+(y﹣2)2=25可得它的圆心为(1,2),半径为5.根据上述材料,结合你所学的知识,完成下列各题.
(1)圆心为C(3,4),半径为2的圆的标准方程为: ;
(2)若已知⊙O的标准方程为:(x﹣2)2+y2=22,圆心为C,请判断点A(3,﹣1)与⊙O的位置关系.
26.如图,平面直角坐标系xOy中,矩形OABC如图放置,点B(4,3),E,F分别为OA,BC边上的中点,动点P从点E出发以每秒2个单位速度沿EO方向向点O运动,同时,动点Q从点F出发以每秒1个单位速度沿FB方向向点B运动.当一个点到达终点时,另一个点随之停止.连接EF、PQ,且EF与PQ相交于点M,连接AM.
(1)求线段AM的长度;
(2)过点A作AH⊥PQ,垂足为点H,连接CH,求线段CH长度的最小值.
27.如图所示,BD,CE是△ABC的高,求证:E,B,C,D四点在同一个圆上.
28.已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点B.C.D.E在以点M为圆心的同一个圆上.
29.如图,⊙O是△ABC的外接圆,∠AOB=96°,∠CAB=60°,点D是的中点.求∠ABD的度数.
30.如图,⊙O为△ABC的外接圆,AB为⊙O直径,AC=BC,点D在劣弧BC上,CE⊥CD交AD于E,连接BD.
(1)求证:△ACE≌△BCD.
(2)若CD=2,BD=3,求⊙O的半径.
(3)若点F为DE的中点,连接CF,FO,设CD=a,BD=b,求CF+FO.(用含有a,b的代数式表示)
参考答案
1.解:如图,连接BO′、BC.
∵CE⊥AD,
∴∠AEC=90°,
∴在点D移动的过程中,点E在以AC为直径的圆上运动,
∵AB是直径,
∴∠ACB=90°,
在Rt△ABC中,∵AC=4,AB=5,
∴BC===3,O′E=2,
在Rt△BCO′中,BO′===,
∵O′E+BE≥O′B,
∴当O′、E、B共线时,BE的值最小,最小值为O′B﹣O′E=﹣2,
故选:B.
2.解:A、已知圆心和半径可以作一个圆,说法正确,故不符合题意.
B、只有确定圆心和半径才能确定一个圆,所以经过一个已知点A的圆能作无数个,说法正确,故不符合题意.
C、只有确定圆心和半径才能确定一个圆,所以已知点A,B的圆能作无数个,说法错误,故符合题意.
D、经过不在同一直线上的三个点A,B,C只能作一个圆,说法正确,故不符合题意.
故选:C.
3.解:∵∠OEC=65°,OE=OC,
∴∠EOC=180°﹣2×65°=50°,
∵D是BC的中点,
∴OE⊥BC,
∴,
∴∠EOB=50°,
∴∠BOC=100°,
∴∠A=50°,
故选:A.
4.解:∵⊙O的半径为5cm,点P到圆心O的距离为7cm,
∴OP>⊙O的半径,
∴点P在⊙O外.
故选:C.
5.解:∵⊙O的直径为4cm,
∴半径为2cm,
∵点P到圆心O的距离OP=3cm>2cm,
∴点P在⊙O外.
故选:A.
6.解:∵点B表示实数6,⊙B半径为4.
∴数轴与⊙B的交点表示的数为2或10,
∵点A表示实数a,点A在⊙B内,
∴2<a<10,
故选:B.
7.解:A、弦不一定是直径,但直径是弦,本选项说法错误,不符合题意;
B、∵半圆小于优弧,
∴半圆是圆中最长的弧说法错误,本选项不符合题意;
C、圆的每一条直径所在的直线都是它的对称轴,本选项说法正确,符合题意;
D、过不在同一直线上的三点可以作一个圆,本选项说法错误,不符合题意;
故选:C.
8.解:第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
9.解:∵∠ACB=50°,
∴∠AOB=100°,
∵AO=BO,
∴∠ABO=(180°﹣100°)÷2=40°,
故选:B.
10.解:如图,连接AO,BO,CO,DO,
∵AB=AC,∠ACB=65°,
∴∠ABC=∠ACB=65°,
∴∠BAC=50°,
∴∠AOC=2∠ABC=130°,∠BOC=2∠BAC=100°,
∵点C是弧BD的中点,
∴,
∴∠BOC=∠COD=100°,
∴∠AOD=30°,
∵∠AOC=2∠ACD,
∴∠ACD=15°,
故选:B.
11.解:∵四边形BEHF是平行四边形,
∴EM=FM,
∵∠EGF=90°,
∴GM=EF,
∴要GM最小,即EF最小,
∵AB=3,BC=2,
设BE=x,则CE=2﹣x,
∵四边形ABCD为矩形,
∴∠ABC=90°,即∠BAE+∠AEB=90°,
∵AE⊥BF,
∴∠CBF+∠AEB=90°,
∴∠CBF=∠BAE,
又∵∠ABE=∠BCF=90°,
∴△ABE∽△BCF,
∴,即=,
∴CF=,
∴EF===,
设y=x2﹣4x+4,
当x=时,y取最小值,
∴EF的最小值为,
故GM的最小值为.
故答案为.
12.解:设直线AB的解析式为y=kx+b,
∵A(1,0),点B(0,2),
∴,
解得,
∴y=﹣2x+2.
解方程组,得,
∴当P的坐标为(2,﹣2)时,过P,A,B三点不能作出一个圆.
故答案为(2,﹣2)
13.解:如图,连接OB,OC,
∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°,
∴∠BAC+∠DHE=360°﹣∠ADC﹣∠AEB=180°,
∵O、H、B、C在同一圆周上,
∴∠BOC=∠BHC=∠DHE,
∴∠BAC+∠BOC=180°,
∵∠BOC=2∠BAC,
∴∠BAC+∠BOC=3∠BAC=180°,
∴∠BAC=60°,
故答案为:60°.
14.解:∵方程x2﹣2x+d=0没有实数根,
∴Δ=b2﹣4ac=4﹣4d<0,
∴d>1,
∵⊙O的半径为1,
∴d>r;
∴点P在⊙O的外部,
故答案为:圆外.
15.
解:以AD所在的直线为对称轴,作正方形ABCD的对称正方形ANMD,
∴MD=CD,MN=AD=2,∠N=90o,
∵H为GC的中点,
∴HD为△GMC的中位线,
∴DH=GM,
∴当GM最短时,DH最短,
∵四边形ABCD是正方形,
∴BA=AD,∠BAE=∠ADF=90°,
∵AE=DF,
∴△ABE≌△DAF,
∴∠ABE=∠DAF,
∵∠BAD=∠BAG+∠DAF=90°,
∴∠ABE+∠DAF=90°,
∴∠ABE+∠BAG=90°,
∴∠AGB=90°,
∴点G在以AB为直径的圆O上,
∴当点G在OM上时,GM最短,
∴OM=,
∴GM=OM﹣OG=﹣1,
∴DH=GM=,
故答案为:.
16.解:如图,延长AC到T,使得CT=AC,连接BT,TE,BE.
∵AC=CT,BC⊥AT,
∴BA=BT,
∵∠ACB=90°,∠ABC=30°,BC=3,
∴∠BAT=60°,AC=BC tan30°=3,
∴AB=2AC=6,
∴△ABT是等边三角形,
∴BT=AB=6,
∵AD=BD=BE,
∴BE=3,
∵ET≤BT+BE,
∴ET≤9,
∴ET的最大值为9,
∵AC=CT,AF=FE,
∴CF=ET,
∴CF的最大值为.
故答案为:.
17.解:∵A(1,3),B(3,3),C(5,1)不在同一直线上
∴经过点A,B,C可以确定一个圆
∴该圆圆心必在线段AB的垂直平分线上
∴设圆心坐标为M(2,m)
则点M在线段BC的垂直平分线上
∴MB=MC
由勾股定理得:=
∴1+m2﹣6m+9=9+m2﹣2m+1
∴m=0
∴圆心坐标为M(2,0)
故答案为:(2,0).
18.解:根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,1).
故答案为:(2,1).
19.解:连接OC,如图所示,
∵OB=OC,
∴∠OCB=∠OBC=40°,
∴∠BOC=100°,
∵∠1+∠BOC=360°,
∴∠1=260°,
∵∠A=∠1,
∴∠A=130°.
故答案为:130.
20.解:作点C的对称点C′,连接C′D,OB,OD.
∴∠BC'D=∠BAD,
由折叠的性质,可知∠BC'D=∠BCD,
∴∠BAC=∠ACB,
∵∠ABC=90°,
∴△ABC是等腰直角三角形,
∴∠BD′C=∠BCD=∠BAD=45°,
∴∠BOD=90°,
∴半径=2.
故答案为:2.
21.解:(1)∵矩形ABCD中AB=3,AD=4,
∴AC=BD==5,
∵AF BD=AB AD,
∴AF==,
同理可得DE=,
在Rt△ADE中,AE==;
(2)∵AF<AB<AE<AD<AC,
∴若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,即点F在圆内,点D、C在圆外,
∴⊙A的半径r的取值范围为2.4<r<4.
22.解:(1)如图所示:分别作弦AB和AC的垂直平分线交点O即为所求的圆心;
(2)连接AO,OB,BC,BC交OA于D.
∵BC=16cm,
∴BD=8cm,
∵AB=10cm,
∴AD=6cm,
设圆片的半径为R,在Rt△BOD中,OD=(R﹣6)cm,
∴R2=82+(R﹣6)2,
解得:R=cm,
∴圆片的半径R为cm.
23.证明:(1)连接AE,如图,
∵∠ADB=90°,
∴AB为直径,
∴∠AEB=90°,
∴AE⊥BC,
∵AB=AC,
∴AE是△ABC的中线,
∴E是BC的中点,
(2)连接DE,如图,
∵E是BC的中点,
∴BC=2CE,
∵BC=2CD,
∴CE=CD,
∴∠CDE=∠CED,
∵四边形ADEB是圆的内接四边形,
∴∠BAD+∠BED=180°.
∵∠CED+∠BED=180°,
∴∠BAD=∠CED,
∵∠ABD=90°﹣∠BAD,∠BCD=180°﹣∠CED﹣∠CDE=180°﹣2∠BAD,
∴∠BCD=2∠ABD.
24.解:(1)∵四边形ABCD是矩形,
∴AD=BC=12cm,CD=AB=6cm,∠A=∠B=∠C=90°,
由题意得:AP=tcm,BQ=2tcm,
∴BP=AB﹣AP=(6﹣t)cm,CQ=BC﹣BQ=(12﹣2t)cm,
当t=2时,AP=2cm,BQ=4cm,BP=AB﹣AP=4cm,CQ=BC﹣BQ=8cm,
∴△DPQ的面积=12×6﹣×12×2﹣×4×4﹣×6×8=28(cm2),
故答案为:28;
(2)∵∠A=90°,
∴A、P、D三点在以DP为直径的圆上,
若点Q也在圆上,则∠PQD=90°,
∵PQ2=(6﹣t)2+(2t)2,DQ2=62+(12﹣2t)2,DP2=t2+122,PQ2+DQ2=DP2,
∴(6﹣t)2+(2t)2+62+(12﹣2t)2=t2+122;
解得t1=6,t2=,
∴当t=6或时A、P、Q、D四点恰好在同一个圆上.
25.解:(1)圆心为C(3,4),半径为2的圆的标准方程为:(x﹣3)2+(y﹣4)2=4.
故答案为:(x﹣3)2+(y﹣4)2=4.
(2)由题意圆心为C(2,0),
∵A(3,﹣1),
∴AC==<2,
∴点A在⊙C内部.
26.解:(1)设运动时间为t秒.则FQ=t,PE=2t.
∵B(4,3),四边形ABCO是矩形,
∴BC=OA=4,AB=OC=3,
∵CF=FB.OE=EA,
∴EF=OC=3,
∵FQ∥PE,
∴==,
∴FM=1.ME=2,
在Rt△AME中,∠AEM=90°,AE=EM=2,
∴AM=2.
(2)由题意,点H在以AM为直径的⊙T的圆上运动,连接CT,CH,TH.
∵A(4,0),M(2,2),MT=AT,
∴T(3,1),
∵C(0,3),
∴CT==,
∵TH=TM=TA=,
∴CH≥CT﹣TH,
∴CH≥﹣,
∴CH的最小值为﹣.
27.证明:如图所示,取BC的中点F,连接DF,EF.
∵BD,CE是△ABC的高,
∴△BCD和△BCE都是直角三角形.
∴DF,EF分别为Rt△BCD和Rt△BCE斜边上的中线,
∴DF=EF=BF=CF.
∴E,B,C,D四点在以F点为圆心,BC为半径的圆上.
28.证明:连接ME、MD,
∵BD、CE分别是△ABC的高,M为BC的中点,
∴ME=MD=MC=MB=BC,
∴点B、C、D、E在以点M为圆心的同一圆上.
29.解:∵∠AOB=96°,
∴∠C=AOB=48°,
∵∠CAB=60°,
∴∠ABC=180°﹣∠C﹣∠CAB=72°,
连接CD,
∴∠D=180°﹣∠CAB=120°,
∵点D是的中点,
∴=,
∴BD=CD,
∴∠CBD=×(180°﹣120°)=30°,
∴∠ABD=∠ABC+∠CBD=72°+30°=102°.
30.解:(1)证明:∵AB为⊙O直径,
∴∠ACB=90°,
∵CE⊥CD,
∴∠ECD=90°,
∴∠ACE=90°﹣∠ECB=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(ASA);
(2)∵△ACE≌△BCD,
∴CE=CD,AE=BD,
∵CE⊥CD,
∴△ECD是等腰直角三角形,
∵CD=2,BD=3,
∴DE=2,AE=3,
∴AD=5,
∵AB为⊙O直径,
∴∠ADB=90°,
∴AB==2,
∴⊙O的半径为;
(3)法一:过O作OH⊥AD于H,如图:
∵△ECD是等腰直角三角形,CD=a,
∴ED=a,
∵F为DE的中点,
∴CF=DF=DE=a,
∵△ACE≌△BCD,
∴AE=BD=b,
∴AD=ED+AE=a+b,
∵OH⊥AD,∠ADB=90°,
∴OH∥BD,
∵AO=OB,
∴DH=AD=a+b,OH=BD=b,
∴HF=DH﹣DF=(a+b)﹣a=b,
在Rt△OHF中,FO==b,
∴CF+FO=a+b.
法二:延长AD至点H,使DH=AE,连接BH,如图:
由(1)得△ACE≌△BCD,
∴BD=AE=DH,
∵AB为直径,
∴∠ADB=∠BDH=90°,
∴△BDH为等腰直角三角形,
∵BD=b,
∴BH=b,
∵△ECD是等腰直角三角形,CD=a,
∴ED=a,CF=a=DF=EF,
而DH=AE,
∴AE+EF=DH+DF,即AF=HF,
∴F为AH中点,
∵O为AB中点,
∴FO=BD=b,
∴CF+FO=a+b.
