鲁教版(五四制)2021-2022学年九年级数学下册5.10圆锥的侧面积 同步练习题(word版、含解析)
文档属性
| 名称 | 鲁教版(五四制)2021-2022学年九年级数学下册5.10圆锥的侧面积 同步练习题(word版、含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 347.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 16:40:55 | ||
图片预览

文档简介
2021-2022学年鲁教版九年级数学下册《5.10圆锥的侧面积》同步练习题(附答案)
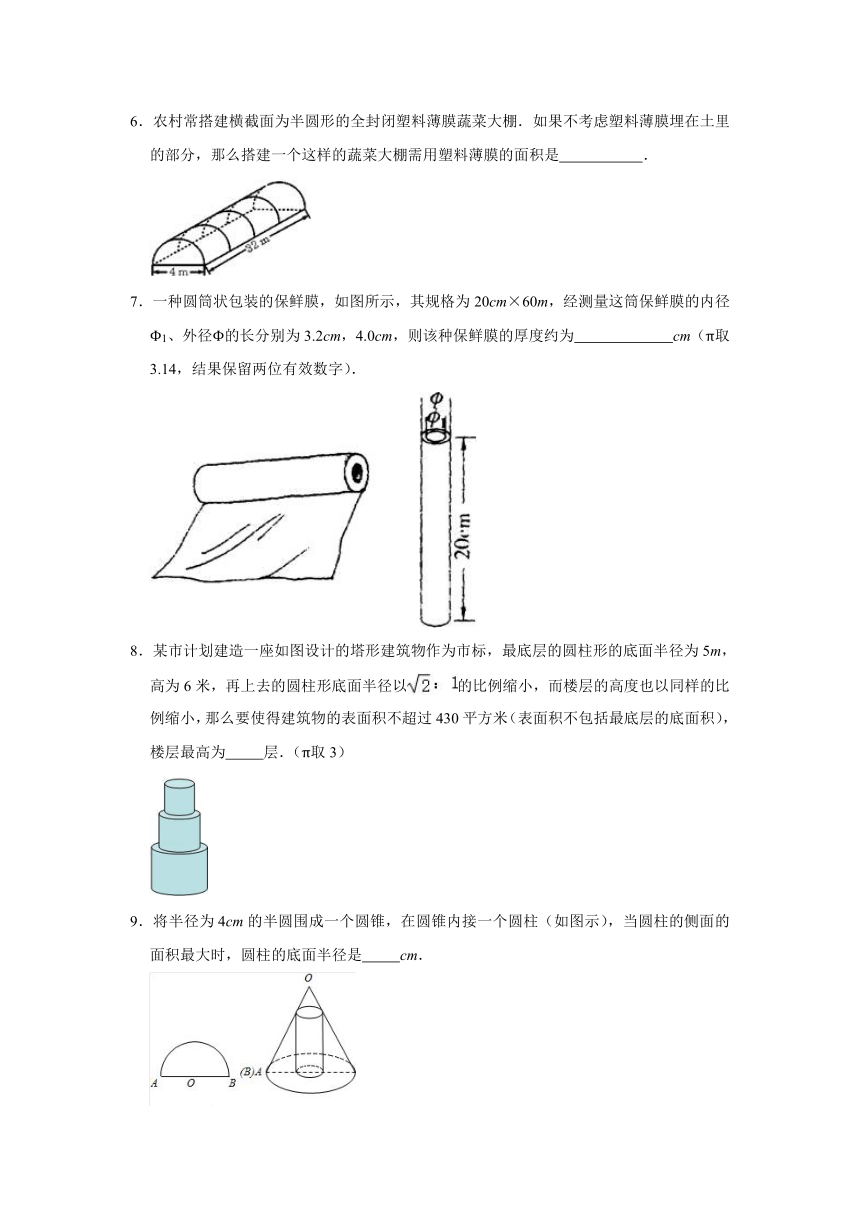
1.如图,将钢球放置到一个倒立的空心透明圆锥中,测得相关数据如图所示(图中数据单位:cm),则钢球的半径为 cm(圆锥的壁厚忽略不计).
2.如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2= .
3.如图,现有一个圆心角为90°,半径为16cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为 cm.
4.如图,从一张腰长为6cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥底面半径为 cm.
5.如图所示,正五边形ABCDE的边长为1,⊙B过五边形的顶点A、C,扇形ABC可以围成一个圆锥的侧面,则该圆锥的侧面积为 .
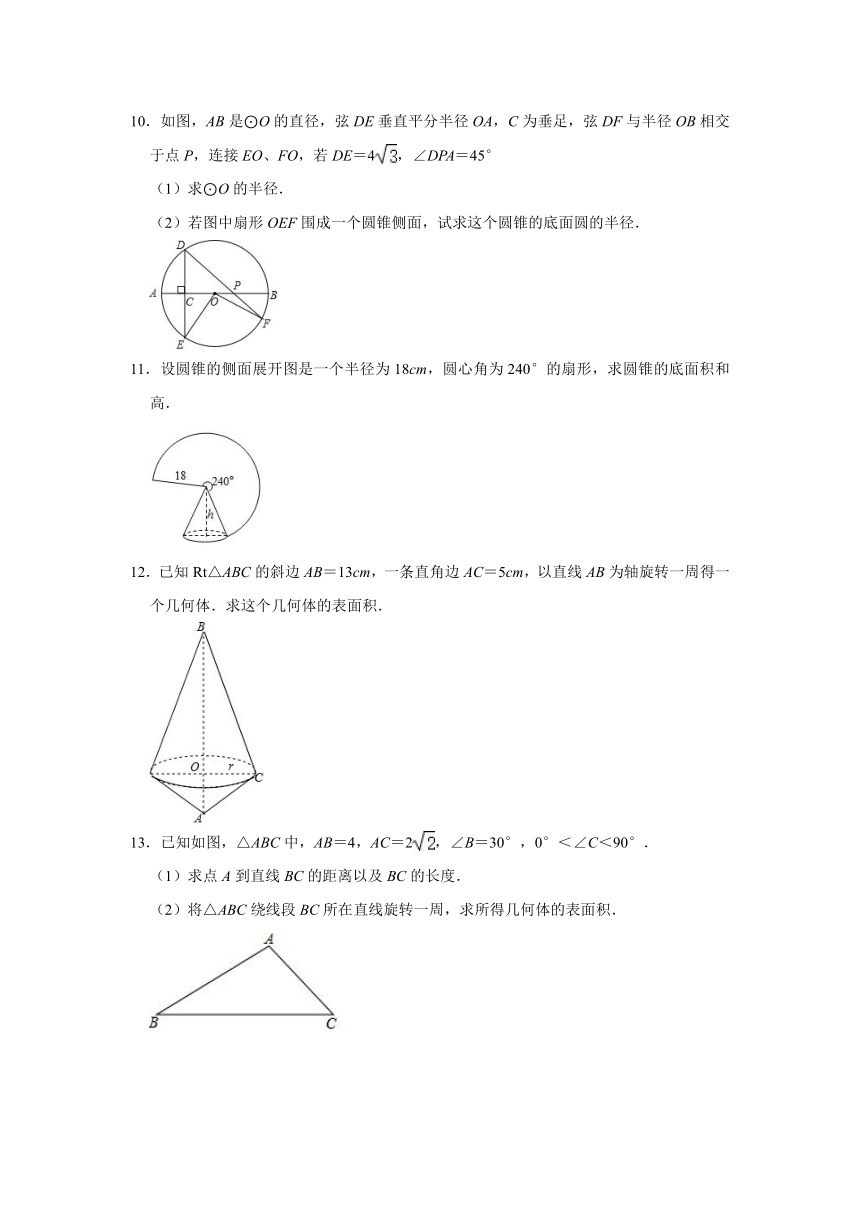
6.农村常搭建横截面为半圆形的全封闭塑料薄膜蔬菜大棚.如果不考虑塑料薄膜埋在土里的部分,那么搭建一个这样的蔬菜大棚需用塑料薄膜的面积是 .
7.一种圆筒状包装的保鲜膜,如图所示,其规格为20cm×60m,经测量这筒保鲜膜的内径Φ1、外径Φ的长分别为3.2cm,4.0cm,则该种保鲜膜的厚度约为 cm(π取3.14,结果保留两位有效数字).
8.某市计划建造一座如图设计的塔形建筑物作为市标,最底层的圆柱形的底面半径为5m,高为6米,再上去的圆柱形底面半径以的比例缩小,而楼层的高度也以同样的比例缩小,那么要使得建筑物的表面积不超过430平方米(表面积不包括最底层的底面积),楼层最高为 层.(π取3)
9.将半径为4cm的半圆围成一个圆锥,在圆锥内接一个圆柱(如图示),当圆柱的侧面的面积最大时,圆柱的底面半径是 cm.
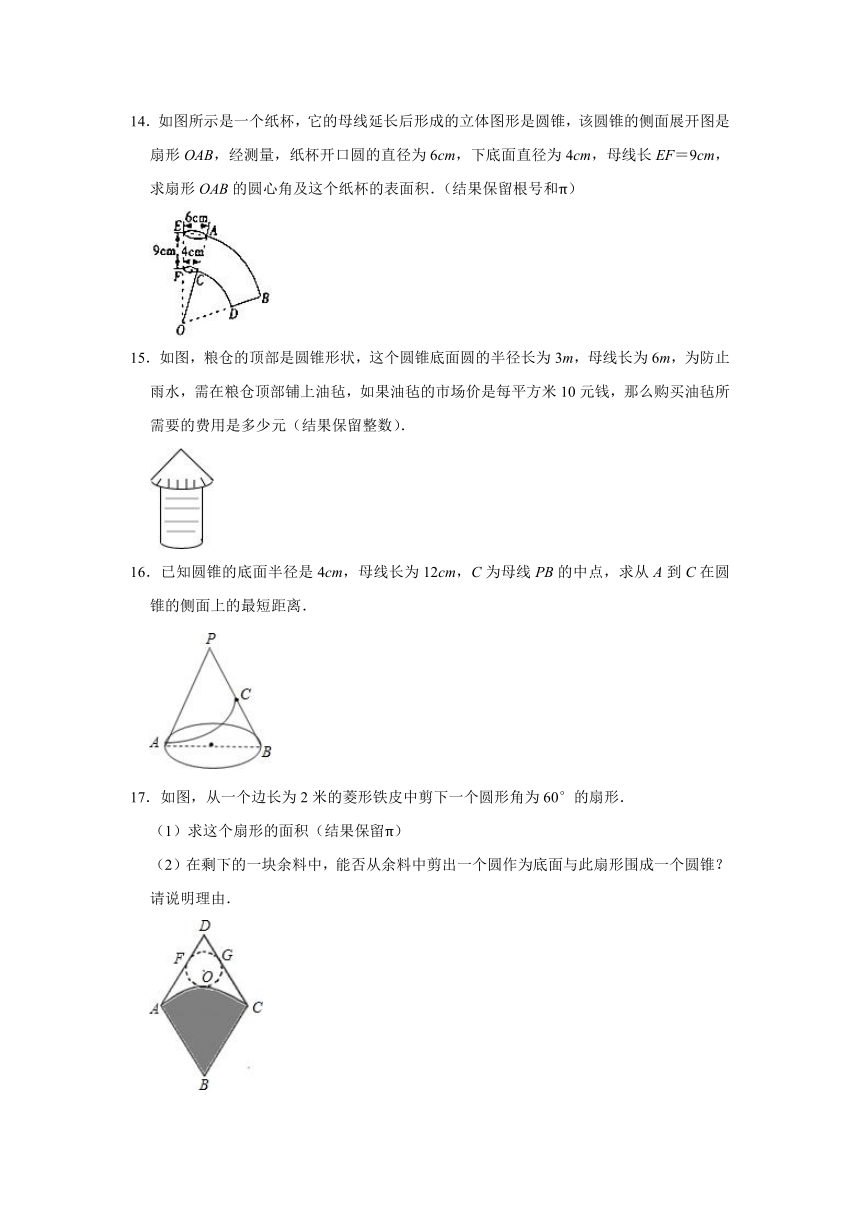
10.如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EO、FO,若DE=4,∠DPA=45°
(1)求⊙O的半径.
(2)若图中扇形OEF围成一个圆锥侧面,试求这个圆锥的底面圆的半径.
11.设圆锥的侧面展开图是一个半径为18cm,圆心角为240°的扇形,求圆锥的底面积和高.
12.已知Rt△ABC的斜边AB=13cm,一条直角边AC=5cm,以直线AB为轴旋转一周得一个几何体.求这个几何体的表面积.
13.已知如图,△ABC中,AB=4,AC=2,∠B=30°,0°<∠C<90°.
(1)求点A到直线BC的距离以及BC的长度.
(2)将△ABC绕线段BC所在直线旋转一周,求所得几何体的表面积.
14.如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6cm,下底面直径为4cm,母线长EF=9cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π)
15.如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是多少元(结果保留整数).
16.已知圆锥的底面半径是4cm,母线长为12cm,C为母线PB的中点,求从A到C在圆锥的侧面上的最短距离.
17.如图,从一个边长为2米的菱形铁皮中剪下一个圆形角为60°的扇形.
(1)求这个扇形的面积(结果保留π)
(2)在剩下的一块余料中,能否从余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由.
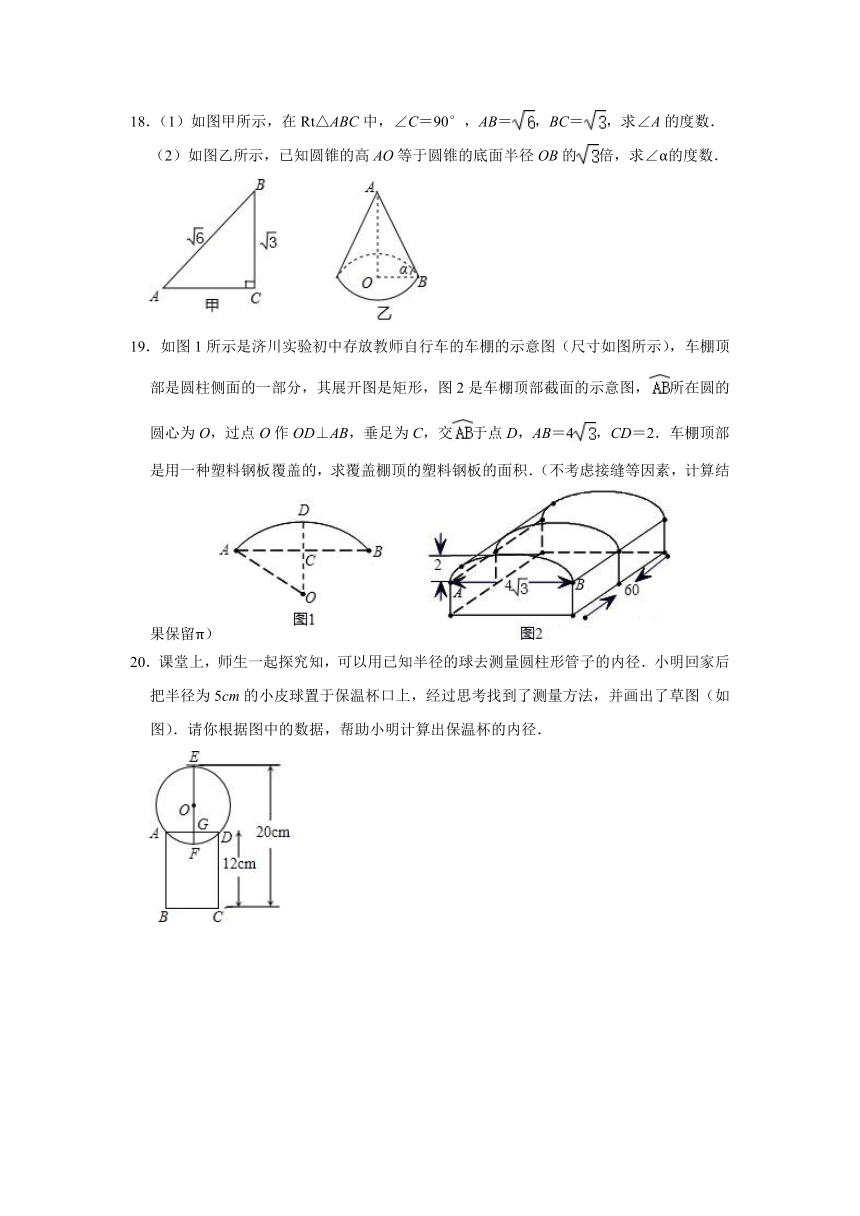
18.(1)如图甲所示,在Rt△ABC中,∠C=90°,AB=,BC=,求∠A的度数.
(2)如图乙所示,已知圆锥的高AO等于圆锥的底面半径OB的倍,求∠α的度数.
19.如图1所示是济川实验初中存放教师自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分,其展开图是矩形,图2是车棚顶部截面的示意图,所在圆的圆心为O,过点O作OD⊥AB,垂足为C,交于点D,AB=4,CD=2.车棚顶部是用一种塑料钢板覆盖的,求覆盖棚顶的塑料钢板的面积.(不考虑接缝等因素,计算结果保留π)
20.课堂上,师生一起探究知,可以用已知半径的球去测量圆柱形管子的内径.小明回家后把半径为5cm的小皮球置于保温杯口上,经过思考找到了测量方法,并画出了草图(如图).请你根据图中的数据,帮助小明计算出保温杯的内径.
参考答案
1.解:AB=12+14=26(cm),
由勾股定理得AE==24(cm),
由△ADO∽△AEB得
=,
∴=,
∴OD=5.
答:钢球的半径为5cm.
故答案为:5.
2.解:如图,连接OA.
∵点O为正六边形ABCDEF的中心,M为AF的中点,
∴OM⊥AF,
∵六边形ABCDEF为正六边形,
∴∠AOM=30°,
设AM=a,
∴AB=AO=2a,OM=,
∵正六边形的中心角为60°,
∴∠MON=120°,
∴扇形MON的弧长为a,
∴r1=a,
同理,扇形DEF的弧长为,
∴r2=,
∴r1:r2=.
故答案为::2.
3.解:圆锥的底面周长是:=8πcm.
设圆锥底面圆的半径是r,则2πr=8π.
解得:r=4cm.
故答案是:4.
4.解:过O作OE⊥AB于E,∵OA=OB=6cm,∠AOB=120°,
∴∠A=∠B=30°,
∴OE=OA=3cm,
∴弧CD的长==2π,
设圆锥的底面圆的半径为r,
则2πr=2π,
解得r=1,
故答案为:1.
5.解:∵五边形ABCDE是正五边形,
∴∠B=(5﹣2)×180°=108°,
∴扇形的面积==π;
故答案为:π.
6.解:塑料膜的面积=2π×32+π×(4÷2)2÷2×2
=64π+4π
=68πm2.
故答案为:68πm2.
7.解:圆筒状保鲜膜的平均直径是(3.2+4.0)÷2=3.6cm,
而保鲜膜长的是60m=6000cm,
因此一共有6000÷(3.14×3.6)=530层,
那么厚度就是:0.5×(4.0﹣3.2)÷530=7.54÷10000=0.000754cm≈7.5×10﹣4cm.
故答案为:7.5×10﹣4.
8.解:最下面的圆柱的侧面积为:2π×5×6=180;
底面积为:π×52=75;
第二个圆柱的侧面积=180×()2=90;
两个圆柱组合的表面积为180+75+90=345;
3个圆柱组合的表面积为345+90×=390;
4个圆柱组合的表面积为390+45×=412.5;
5个圆柱组合的表面积为412.5+22.5×=423.75;
6个圆柱组合的表面积为423.75+11.25×=429.375;
7个圆柱组合的表面积为429.375+×5.625>430,
所以最高为6层.
9.解:扇形的弧长=4πcm,
∴圆锥的底面半径=4π÷2π=2cm,
∴圆锥的高为=2cm,
设圆柱的底面半径为rcm,高为Rcm.
=,
解得:R=2﹣r,
∴圆柱的侧面积=2π×r×(2﹣r)=﹣2πr2+4πr(cm2),
∴当r==1cm时,圆柱的侧面积有最大值.
10.解:(1)∵弦DE垂直平分半径OA,
∴CE=DC=DE=2,OC=OE,
∴∠OEC=30°,
∴OC==2,
∴OE=2OC=4,
即⊙O的半径为4;
(2)∵∠DPA=45°,
∴∠D=45°,
∴∠EOF=2∠D=90°,
设这个圆锥的底面圆的半径为r,
∴2πr=,解得r=1,
即这个圆锥的底面圆的半径为1.
11.解:圆锥的弧长为:=24π,
∴圆锥的底面半径为24π÷2π=12,
∴圆锥的底面积为π×122=144π,
∴圆锥的高为=6.
12.解:∵Rt△ABC的斜边AB=13cm,直角边AC=5cm,
∴另一直角边BC=12cm,
以斜边AB为轴旋转一周,得到由两个圆锥组成的几何体,
直角三角形的斜边上的高OC==cm,
则以cm为半径的圆的周长=πcm,
几何体的表面积=×π×(5+12)=π(cm2).
13.解:(1)作AD⊥BC于D,如图,
在Rt△ABD中,∵∠B=30°,
∴AD=AB=2,BD=AD=2,
在Rt△ACD中,CD==2,
∴BC=BD+CD=2+2;
(2)将△ABC绕线段BC所在直线旋转一周,所得几何体的表面积= 2π 2 4+ 2π 2 2=8π+4π.
14.解:由题意可知:=6πcm,=4π,设∠AOB=n,AO=R,则CO=R﹣9,
由弧长公式得:l=,
∴,
解得:n=40,R=27,
故扇形OAB的圆心角是40度.
∵R=27,R﹣9=18,
∴S扇形OCD=×4π×18=36π(cm2),
S扇形OAB=×6π×27=81π(cm2),
纸杯侧面积=S扇形OAB﹣S扇形OCD=81π﹣36π=45π(cm2),
纸杯底面积=π 22=4π(cm2)
纸杯表面积=45π+4π=49π(cm2).
15.解:底面半径为3m,则底面周长=6π,
侧面面积=×6π×6=18πm2,
故所需要的费用=18π×10=180π≈566(元).
答:购买油毡所需要的费用是556元.
16.解:圆锥的底面周长是8π,则8π=,
∴n=120°,
即圆锥侧面展开图的圆心角是120度.
∴∠APB=60°,
∵PA=PB,
∴△PAB是等边三角形,
∵C是PB中点,
∴AC⊥PB,
∴∠ACP=90度.
∵在圆锥侧面展开图中AP=12,PC=6,
∴在圆锥侧面展开图中AC==6cm.
最短距离是6cm.
17.解:(1)如图∵AB=AC=2,
∴;
(2)连接AC、BD,BD交弧AC于E点,圆心在DE上
由勾股定理:BD=2,DE=,
弧AC的长:,
∴,
∴<1.46=DE,
另一方面,如图:由于∠ADE=30°,过O作OF⊥AD,则OD=2OF=2r,因此DE≥3r
所以能在余料中剪出一个圆作为底面与此扇形围成圆锥.
18.解:(1)∵在Rt△ABC中,∠C=90°,AB=,BC=,sinA=,
∴sinA=,
∴∠A=45°;
(2)由已知可得,
∠AOB=90°,AO=OB,
∴tan∠α===,
∴∠α=60°.
19.解:∵OD⊥AB,
∴AC=2,
∵CD=2,
∴OC=OA﹣2,
∵OA2﹣OC2=AC2
∴OA=4,
∴sin∠AOD=,
∴∠AOD=60°,
∴∠AOB=2∠AOD=120°
∴覆盖棚顶的塑料钢板的面积=×60=160π.
20.解:连OD.
∵EG=20﹣12=8,
∴OG=8﹣5=3,
∴GD=4,
∴AD=2GD=8cm.
答:保温杯的内径为8cm.
1.如图,将钢球放置到一个倒立的空心透明圆锥中,测得相关数据如图所示(图中数据单位:cm),则钢球的半径为 cm(圆锥的壁厚忽略不计).
2.如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2= .
3.如图,现有一个圆心角为90°,半径为16cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为 cm.
4.如图,从一张腰长为6cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥底面半径为 cm.
5.如图所示,正五边形ABCDE的边长为1,⊙B过五边形的顶点A、C,扇形ABC可以围成一个圆锥的侧面,则该圆锥的侧面积为 .
6.农村常搭建横截面为半圆形的全封闭塑料薄膜蔬菜大棚.如果不考虑塑料薄膜埋在土里的部分,那么搭建一个这样的蔬菜大棚需用塑料薄膜的面积是 .
7.一种圆筒状包装的保鲜膜,如图所示,其规格为20cm×60m,经测量这筒保鲜膜的内径Φ1、外径Φ的长分别为3.2cm,4.0cm,则该种保鲜膜的厚度约为 cm(π取3.14,结果保留两位有效数字).
8.某市计划建造一座如图设计的塔形建筑物作为市标,最底层的圆柱形的底面半径为5m,高为6米,再上去的圆柱形底面半径以的比例缩小,而楼层的高度也以同样的比例缩小,那么要使得建筑物的表面积不超过430平方米(表面积不包括最底层的底面积),楼层最高为 层.(π取3)
9.将半径为4cm的半圆围成一个圆锥,在圆锥内接一个圆柱(如图示),当圆柱的侧面的面积最大时,圆柱的底面半径是 cm.
10.如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EO、FO,若DE=4,∠DPA=45°
(1)求⊙O的半径.
(2)若图中扇形OEF围成一个圆锥侧面,试求这个圆锥的底面圆的半径.
11.设圆锥的侧面展开图是一个半径为18cm,圆心角为240°的扇形,求圆锥的底面积和高.
12.已知Rt△ABC的斜边AB=13cm,一条直角边AC=5cm,以直线AB为轴旋转一周得一个几何体.求这个几何体的表面积.
13.已知如图,△ABC中,AB=4,AC=2,∠B=30°,0°<∠C<90°.
(1)求点A到直线BC的距离以及BC的长度.
(2)将△ABC绕线段BC所在直线旋转一周,求所得几何体的表面积.
14.如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6cm,下底面直径为4cm,母线长EF=9cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π)
15.如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是多少元(结果保留整数).
16.已知圆锥的底面半径是4cm,母线长为12cm,C为母线PB的中点,求从A到C在圆锥的侧面上的最短距离.
17.如图,从一个边长为2米的菱形铁皮中剪下一个圆形角为60°的扇形.
(1)求这个扇形的面积(结果保留π)
(2)在剩下的一块余料中,能否从余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由.
18.(1)如图甲所示,在Rt△ABC中,∠C=90°,AB=,BC=,求∠A的度数.
(2)如图乙所示,已知圆锥的高AO等于圆锥的底面半径OB的倍,求∠α的度数.
19.如图1所示是济川实验初中存放教师自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分,其展开图是矩形,图2是车棚顶部截面的示意图,所在圆的圆心为O,过点O作OD⊥AB,垂足为C,交于点D,AB=4,CD=2.车棚顶部是用一种塑料钢板覆盖的,求覆盖棚顶的塑料钢板的面积.(不考虑接缝等因素,计算结果保留π)
20.课堂上,师生一起探究知,可以用已知半径的球去测量圆柱形管子的内径.小明回家后把半径为5cm的小皮球置于保温杯口上,经过思考找到了测量方法,并画出了草图(如图).请你根据图中的数据,帮助小明计算出保温杯的内径.
参考答案
1.解:AB=12+14=26(cm),
由勾股定理得AE==24(cm),
由△ADO∽△AEB得
=,
∴=,
∴OD=5.
答:钢球的半径为5cm.
故答案为:5.
2.解:如图,连接OA.
∵点O为正六边形ABCDEF的中心,M为AF的中点,
∴OM⊥AF,
∵六边形ABCDEF为正六边形,
∴∠AOM=30°,
设AM=a,
∴AB=AO=2a,OM=,
∵正六边形的中心角为60°,
∴∠MON=120°,
∴扇形MON的弧长为a,
∴r1=a,
同理,扇形DEF的弧长为,
∴r2=,
∴r1:r2=.
故答案为::2.
3.解:圆锥的底面周长是:=8πcm.
设圆锥底面圆的半径是r,则2πr=8π.
解得:r=4cm.
故答案是:4.
4.解:过O作OE⊥AB于E,∵OA=OB=6cm,∠AOB=120°,
∴∠A=∠B=30°,
∴OE=OA=3cm,
∴弧CD的长==2π,
设圆锥的底面圆的半径为r,
则2πr=2π,
解得r=1,
故答案为:1.
5.解:∵五边形ABCDE是正五边形,
∴∠B=(5﹣2)×180°=108°,
∴扇形的面积==π;
故答案为:π.
6.解:塑料膜的面积=2π×32+π×(4÷2)2÷2×2
=64π+4π
=68πm2.
故答案为:68πm2.
7.解:圆筒状保鲜膜的平均直径是(3.2+4.0)÷2=3.6cm,
而保鲜膜长的是60m=6000cm,
因此一共有6000÷(3.14×3.6)=530层,
那么厚度就是:0.5×(4.0﹣3.2)÷530=7.54÷10000=0.000754cm≈7.5×10﹣4cm.
故答案为:7.5×10﹣4.
8.解:最下面的圆柱的侧面积为:2π×5×6=180;
底面积为:π×52=75;
第二个圆柱的侧面积=180×()2=90;
两个圆柱组合的表面积为180+75+90=345;
3个圆柱组合的表面积为345+90×=390;
4个圆柱组合的表面积为390+45×=412.5;
5个圆柱组合的表面积为412.5+22.5×=423.75;
6个圆柱组合的表面积为423.75+11.25×=429.375;
7个圆柱组合的表面积为429.375+×5.625>430,
所以最高为6层.
9.解:扇形的弧长=4πcm,
∴圆锥的底面半径=4π÷2π=2cm,
∴圆锥的高为=2cm,
设圆柱的底面半径为rcm,高为Rcm.
=,
解得:R=2﹣r,
∴圆柱的侧面积=2π×r×(2﹣r)=﹣2πr2+4πr(cm2),
∴当r==1cm时,圆柱的侧面积有最大值.
10.解:(1)∵弦DE垂直平分半径OA,
∴CE=DC=DE=2,OC=OE,
∴∠OEC=30°,
∴OC==2,
∴OE=2OC=4,
即⊙O的半径为4;
(2)∵∠DPA=45°,
∴∠D=45°,
∴∠EOF=2∠D=90°,
设这个圆锥的底面圆的半径为r,
∴2πr=,解得r=1,
即这个圆锥的底面圆的半径为1.
11.解:圆锥的弧长为:=24π,
∴圆锥的底面半径为24π÷2π=12,
∴圆锥的底面积为π×122=144π,
∴圆锥的高为=6.
12.解:∵Rt△ABC的斜边AB=13cm,直角边AC=5cm,
∴另一直角边BC=12cm,
以斜边AB为轴旋转一周,得到由两个圆锥组成的几何体,
直角三角形的斜边上的高OC==cm,
则以cm为半径的圆的周长=πcm,
几何体的表面积=×π×(5+12)=π(cm2).
13.解:(1)作AD⊥BC于D,如图,
在Rt△ABD中,∵∠B=30°,
∴AD=AB=2,BD=AD=2,
在Rt△ACD中,CD==2,
∴BC=BD+CD=2+2;
(2)将△ABC绕线段BC所在直线旋转一周,所得几何体的表面积= 2π 2 4+ 2π 2 2=8π+4π.
14.解:由题意可知:=6πcm,=4π,设∠AOB=n,AO=R,则CO=R﹣9,
由弧长公式得:l=,
∴,
解得:n=40,R=27,
故扇形OAB的圆心角是40度.
∵R=27,R﹣9=18,
∴S扇形OCD=×4π×18=36π(cm2),
S扇形OAB=×6π×27=81π(cm2),
纸杯侧面积=S扇形OAB﹣S扇形OCD=81π﹣36π=45π(cm2),
纸杯底面积=π 22=4π(cm2)
纸杯表面积=45π+4π=49π(cm2).
15.解:底面半径为3m,则底面周长=6π,
侧面面积=×6π×6=18πm2,
故所需要的费用=18π×10=180π≈566(元).
答:购买油毡所需要的费用是556元.
16.解:圆锥的底面周长是8π,则8π=,
∴n=120°,
即圆锥侧面展开图的圆心角是120度.
∴∠APB=60°,
∵PA=PB,
∴△PAB是等边三角形,
∵C是PB中点,
∴AC⊥PB,
∴∠ACP=90度.
∵在圆锥侧面展开图中AP=12,PC=6,
∴在圆锥侧面展开图中AC==6cm.
最短距离是6cm.
17.解:(1)如图∵AB=AC=2,
∴;
(2)连接AC、BD,BD交弧AC于E点,圆心在DE上
由勾股定理:BD=2,DE=,
弧AC的长:,
∴,
∴<1.46=DE,
另一方面,如图:由于∠ADE=30°,过O作OF⊥AD,则OD=2OF=2r,因此DE≥3r
所以能在余料中剪出一个圆作为底面与此扇形围成圆锥.
18.解:(1)∵在Rt△ABC中,∠C=90°,AB=,BC=,sinA=,
∴sinA=,
∴∠A=45°;
(2)由已知可得,
∠AOB=90°,AO=OB,
∴tan∠α===,
∴∠α=60°.
19.解:∵OD⊥AB,
∴AC=2,
∵CD=2,
∴OC=OA﹣2,
∵OA2﹣OC2=AC2
∴OA=4,
∴sin∠AOD=,
∴∠AOD=60°,
∴∠AOB=2∠AOD=120°
∴覆盖棚顶的塑料钢板的面积=×60=160π.
20.解:连OD.
∵EG=20﹣12=8,
∴OG=8﹣5=3,
∴GD=4,
∴AD=2GD=8cm.
答:保温杯的内径为8cm.
