2021-2022学年北师大版七年级数学上册第五章 一元一次方程 单元检测
文档属性
| 名称 | 2021-2022学年北师大版七年级数学上册第五章 一元一次方程 单元检测 |  | |
| 格式 | docx | ||
| 文件大小 | 70.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 20:00:42 | ||
图片预览




文档简介
北师大版七年级上册第五章
一元一次方程
一、单选题
1.若关于x的一元一次方程2k﹣x﹣4=0的解是x=﹣3,那么k的值是( )
A. B. C. 6 D. 10
2.把方程 去分母后,正确的是( ).
A. B.
C. D.
3.B是线段AD上一动点,沿A至D的方向以 的速度运动.C是线段BD的中点. .在运动过程中,若线段AB的中点为E.则EC的长是( )
A. B. C. 或 D. 不能确定
4.一件商品按成本价提高30%后标价,再打8折(标价的80%)销售,售价为312元,设这件商品的成本价为x元,根据题意,下面所列的方程正确的是( )
A. x·30%×80%=312 B. x·30%=312×80%
C. 312×30%×80%=x D. x(1+30%)×80%=312
5.某药店经营的抗病毒药品,在市场紧缺的情况下提价100%,物价部门查处后,限定其提价的幅度只能是原价的10%,则该药品现在降价的幅度是( )
A. 45% B. 50% C. 90% D. 95%
6.阅读:关于x方程ax=b在不同的条件下解的情况如下:(1)当a≠0时,有唯一解x= ;(2)当a=0,b=0时有无数解;(3)当a=0,b≠0时无解.请你根据以上知识作答:已知关于x的方程 a= ﹣ (x﹣6)无解,则a的值是( )
A. 1 B. ﹣1 C. ±1 D. a≠1
7.甲车与乙车同时从A地出发去往B地,如图所示,折线O-A-B-C和射线OC分别是甲、乙两车行进过程中路程与时间的关系,已知甲车中途有事停留36分钟后再继续前往C地,两车同时到达C地,则下列说法:①乙车的速度为70千米/时;②甲车再次出发后的速度为100千米/时;③两车在到达B地前不会相遇;④甲车再次出发时,两车相距60千米。其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
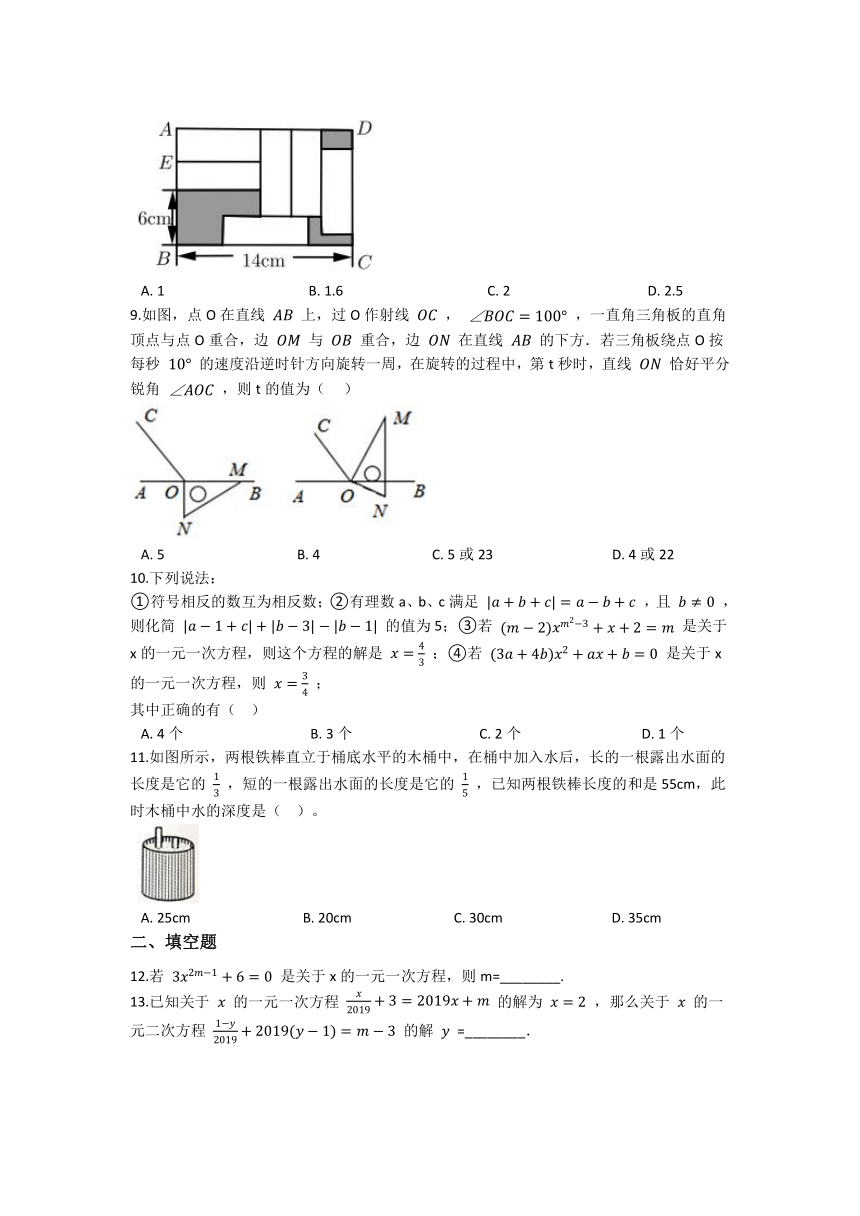
8.在长方形 中,放入6个形状大小完全相同的小长方形,所标尺寸如图所示,则小长方形的宽 的长度为( ) cm .
A. 1 B. 1.6 C. 2 D. 2.5
9.如图,点O在直线 上,过O作射线 , ,一直角三角板的直角顶点与点O重合,边 与 重合,边 在直线 的下方.若三角板绕点O按每秒 的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线 恰好平分锐角 ,则t的值为( )
A. 5 B. 4 C. 5或23 D. 4或22
10.下列说法:
①符号相反的数互为相反数;②有理数a、b、c满足 ,且 ,则化简 的值为5;③若 是关于x的一元一次方程,则这个方程的解是 ;④若 是关于x的一元一次方程,则 ;
其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
11.如图所示,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,长的一根露出水面的长度是它的 ,短的一根露出水面的长度是它的 ,已知两根铁棒长度的和是55cm,此时木桶中水的深度是( )。
A. 25cm B. 20cm C. 30cm D. 35cm
二、填空题
12.若 是关于x的一元一次方程,则m=________.
13.已知关于 的一元一次方程 的解为 ,那么关于 的一元二次方程 的解 =________.
14.家住山脚下的小明从家出发登山游玩,他下山的速度比上山的速度快 ,他上山 到达的位置离山顶还有 ,到山顶后抄近路下山,下山路程比上山路程近 ,下山用了 ,那么小明上山的路程(到山顶)为 .
15.当x=________时,式子 与 的值互为相反数.
16.已知关于x的一元一次方程 +5=2019x+m的解为x=2018,那么关于y的一元一次方程 ﹣5=2019(5﹣y)﹣m的解为________.
17.如图,在数轴上A点表示数﹣2,B点表示数6,若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,则经过________秒,甲、乙两小球到原点的距离相等.
18.A、B两地之间的公路长108千米,小光骑自行车从A地到B地,小明骑自行车从B地到A地,两人都沿这条公路匀速前进,其中两人的速度都小于27千米/时.若同时出发3小时相遇,则经过________小时两人相距36千米.
三、解答题
19.列方程解应用题:
为参加学校运动会,七年级一班和七年级二班准备购买运动服. 下面是某服装厂给出的运动服价格表:
购买服装数(套) 1~35 36~60 61及61以上
每套服装价(元) 60 50 40
已知两班共有学生67人(每班学生人数都不超过60人),如果两班单独购买服装,每人只买一套,那么一共应付3650元. 问七年级一班和七年级二班各有学生多少人?
20.昨天老师带着我们班同学去深圳少年宫玩,我们一共去了 60人(包括老师),买门票共花了1240元.玩得可开心了!
小明:真羡慕你们,不过听说门票还是挺贵的.
小红:是的,老师票每张30元,学生票每张20元.那你能猜出我们去了几位老师,几位学生吗?
小明:去了……
根据以上的对话,你能用解方程的知识帮助小明回答小红的提问吗?
21.某地的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元;经粗加工后销售,每吨利润4000元;经精加工后销售,每吨利润7000元.当地一家公司现有这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果对蔬菜进行精加工,每天可加工6吨;但每天两种方式不能同时进行.受季节等条件的限制,必须用15天时间将这批蔬菜
全部销售或加工完毕.为此,公司研制了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能地对蔬菜进行精加工,没来得及加工的蔬菜,在市场上直接出售;
方案三:将一部分蔬菜进行精加工,其余蔬菜进行粗加工,并刚好15天完成.
如果你是公司经理,你会选择哪一种方案,请说说理由.
22.一艘船从甲码头到乙码头顺流而行,用了2小时,从乙码头返回甲码头逆流而行,用了3小时,已知水流的速度是每小时3千米, 求船在静水中的平均速度.
23.甲、乙二人同时从相距 千米的A地去B地,甲骑车,乙步行.甲每小时的速度比乙每小时的速度的3倍多1千米,甲达到B地后停留45分,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3小时,求两人的速度各是多少?
答案解析部分
一、单选题
1.【答案】 A
【考点】一元一次方程的解
【解析】【解答】解:∵关于x的一元一次方程2k﹣x﹣4=0的解是x=﹣3,
∴2k+3﹣4=0,
解得:k= ,
故答案为:A.
【分析】将x=﹣3代入2k﹣x﹣4=0中,即可求出k值.
2.【答案】 D
【考点】解含分数系数的一元一次方程
【解析】【解答】去分母得:3x-2(x-1)=6,
故答案为:D.
【分析】将方程两边都乘以6去分母计算即可。
3.【答案】 B
【考点】线段的中点,一元一次方程的实际应用-行程问题
【解析】【解答】设运动时间为t,
则AB=2t,BD=10-2t,
∵C是线段BD的中点,E为线段AB的中点,
∴EB= =t,BC= =5-t,
∴EC=EB+BC=t+5-t=5cm,
故答案为:B.
【分析】根据线段中点的性质,做出线段AD,按要求标出各点大致位置,列出EB,BC的表达式,即可求出线段EC.
4.【答案】 D
【考点】一元一次方程的实际应用-销售问题
【解析】【解答】设这件商品的成本价为x元,成本价提高30%后的标价为x(1+30%),再打8折的售价表示为x(1+30%)×80%,又因售价为312元,
列方程为:x(1+30%)×80%=312.
故答案为:D.
【分析】按成本价的30%标价,则标价为成本价的(1+30%),打八折即用标价×80%,即可得到售价,进而列出方程.
5.【答案】 A
【考点】一元一次方程的实际应用-销售问题
【解析】【解答】解:设药品的原价为a元,药品现在降价x,则根据题意可得:a(1+100%)(1-x)=a(1+10%),
解得x=45%,
故答案为:A.
【分析】设药品的原价为a元,药品现在降价x,根据提价后的价格×(1-x)=降价后的价格,列出方程,解之即可.
6.【答案】 A
【考点】解一元一次方程
【解析】【解答】要把原方程变形化简,去分母得:2ax=3x﹣(x﹣6),
去括号得:2ax=2x+6,
移项,合并得,x= ,
因为无解,所以a﹣1=0,即a=1.
故答案为:A.
【分析】对方程去分母、去括号、移项、合并同类项进行求解,再根据方程无解得到关于a的方程,求解可得a的值.
7.【答案】 C
【考点】一元一次方程的实际应用-行程问题
【解析】【解答】解:① 、由图可知: V乙=3004=75 千米/时 ,故 ① 不正确;
② 、由图可知:甲车再次出发的速度,V甲=(300-60)(4-1.6)=100千米/时,故 ②正确;
③ 、 由图可知:两车在到达B地前不会相遇 ,故 ③正确;
④ 、 由图和①可知: 点B的时间=1+3660=1.6小时;V乙=75 千米/时,S乙=75 1.6=120千米, 甲车再次出发时, 两车之间的距 离=120-60=60千米,故 ④正确.
【分析】由图可知:总路程是300千米,乙车一直在匀速行驶,乙车用时4小时,甲车前一个小时匀速行驶,休息了36分钟(3660=0.6小时),再次提速匀速行驶,在4小时的时候甲乙两车同时到达目的地,即甲乙两车在目的地相遇.
8.【答案】 C
【考点】一元一次方程的实际应用-几何问题
【解析】【解答】解:设AE=xcm,
依题意,得:6+2x=x+(14 3x),
解得:x=2
故答案为:C.
【分析】设AE=xcm,得出大长方形的宽为(6+2x)cm,小长方形的长为(14-3x)cm,从而得出大长方形的宽为(x+14-3x)cm,根据用两个不同的式子表示同一个量,则这两个式子应该相等,从而列出方程,解方程求出x的值,即可求解.
9.【答案】 C
【考点】角的运算,一元一次方程的实际应用-几何问题
【解析】【解答】解:∵ ,
∴ ,
①如图,
当 的反向延长线恰好平分锐角 时,
∴ ,
此时,三角板旋转的角度为 ,
∴ ;
②如图,
当 在 的内部时,
∴∠CON= ∠AOC=40°,
∴三角板旋转的角度为90°+100°+40°=230°,
∴ ;
∴t的值为:5或23.
故答案为: C .
【分析】先求出 ,再分类讨论,进行计算求解即可。
10.【答案】 D
【考点】相反数及有理数的相反数,绝对值及有理数的绝对值,一元一次方程的定义
【解析】【解答】解:仅仅只有符号不同的两个数互为相反数,故①错误;
由 ,且 ,
所以:
< < <
故②错误;
是关于x的一元一次方程,
或 ( )或 ,
或 或
或
当 时,原方程为:
当 时,原方程化为:
,不合题意舍去,
当 时,原方程化为:
综上:方程的解为: 或 故③错误;
是关于x的一元一次方程,
,
故④正确;
故答案为:D
【分析】
11.【答案】 B
【考点】一元一次方程的实际应用-几何问题
【解析】【解答】解:设木桶中水的深度为h,由题意有
整理得:
解得:h=20
故答案为:B
【分析】根据题意长的铁棒在水里的长度为它的 , 所以长的铁棒的长度为 , 短的铁棒在水里的长度为它的 , 所以短的铁棒的长度为 , 根据两根铁棒长度的和是55cm列方程即可得到答案.
二、填空题
12.【答案】 1
【考点】一元一次方程的定义
【解析】【解答】∵ 是关于x的一元一次方程,
∴2m-1=1
解得m=1
故填:1.
【分析】只含有一个未知数,且未知数的次数是1的整式方程,叫做一元一次方程,据此解答即可.
13.【答案】 -1
【考点】一元一次方程的解
【解析】【解答】解:根据题意可得:
对原方程进行变形:
,
,
,
再把 代入上式得出: ,
故答案为: .
【分析】对原方程进行变形可以得出一个等式: ,此时 ,与所求方程进行比较可得出结果.
14.【答案】 5
【考点】一元一次方程的实际应用-行程问题
【解析】【解答】解:设小明上山的速度为xkm/h,
根据题意得:2x+1=(x+1)+2,
解这个方程得:x=2km/h,
经检验符合题意,
2x+1=4+1=5km,
答:小明上山的路程为5km,
故答案为:5.
【分析】先求出2x+1=(x+1)+2,再解方程求解即可。
15.【答案】
【考点】相反数及有理数的相反数,解含分数系数的一元一次方程
【解析】【解答】由题意得: ,去分母得:2(2x+5)+3(x+11)+12x=0,去括号得:4x+10+3x+33+12x=0,移项、合并同类项得:19x=﹣43,系数化1得:x= .故答案为 .
【分析】先根据互为相反数的和为0列出方程 , 然后再根据解方程的一般步骤①两边同时乘以各分母的最小公倍数去分母;②根据乘法的分配律去括号(不要漏乘);③移项(注意改变符号);④ 合并同类项;⑤系数化为1解方程即可.
16.【答案】 2023
【考点】一元一次方程的解
【解析】【解答】解:根据题意得:
方程 可整理得: ,
则该方程的解为x=2018,
方程 可整理得: ,
令n=5﹣y,
则原方程可整理得: ,
则n=﹣2018,
即5﹣y=﹣2018,
解得:y=2023,
故答案为:2023.
【分析】将方程整理可得 , 则该方程的解为x=2018;将关于y的方程整理为 , 令n=5﹣y,可得出 , 从而可得5﹣y=n﹣2018,求出y值即可.
17.【答案】 或8
【考点】数轴及有理数在数轴上的表示,一元一次方程的实际应用-行程问题
【解析】【解答】解:设经过t秒,甲、乙两小球到原点的距离相等.
∵甲球运动的路程为:1 t=t,OA=2,
∴甲球与原点的距离为:t+2;
乙球到原点的距离分两种情况:当0<t≤3时,乙球从点B处开始向左运动,一直到原点O,
∵OB=6,乙球运动的路程为:2 t=2t,乙到原点的距离:6﹣2t(0≤t≤3);
当t>3时,乙球从原点O处开始一直向右运动,此时乙球到原点的距离为:2t﹣6 (t>3).
分两种情况:
①当0<t≤3时,得t+2=6﹣2t,解得t= ;
当t>3时,得t+2=2t﹣6,解得t=8.
故当t= 或8秒时,甲乙两小球到原点的距离相等.
故答案为 或8.
【分析】设经过t秒,甲、乙两小球到原点的距离相等.分两种情况:①0<t≤3,②t>3,根据甲、乙两小球到原点的距离相等列出关于t的方程,解方程即可.
18.【答案】 2或4
【考点】一元一次方程的实际应用-行程问题
【解析】【解答】设经过x小时两人相距36千米,
∵同时出发3小时相遇,
∴可得两人的速度和为: 千米/小时,
①两人相遇前相距36千米,
解得: ;
②两人相遇后相距36千米,
解得: ;
综上,经过2小时或4小时两人相距36千米,
故答案为:2或4.
【分析】先求出两人的速度和为36千米/小时,再分类讨论,列方程求解即可。
三、解答题
19.【答案】 解:∵
∴所以一定有一个班的人数大于35人.
设大于35人的班有学生x人,则另一班有学生(67-x)人,
依题意得
答:七年级一班有37人,七年级二班有30人;或者七年级一班有30人,七年级二班有37人.
【考点】一元一次方程的实际应用-销售问题
【解析】【分析】首先根据题中表格数据得出有一个班的人数大于35人,接着设大于35人的班有学生x人,根据等量关系列出方程,求解即可.
20.【答案】 解:设去了x名学生,(60-x)名老师,依题意得:
30(60-x)+20x=1240,
解之得:x=56,
所以老师: 60-56=4名,
答:共去了4位老师,56位学生.
【考点】一元一次方程的实际应用-销售问题
【解析】【分析】设去了x名学生,(60-x)名老师,根据买门票共花了1240元,列方程进行求解即可得.
21.【答案】 解:方案一:获利 元,
方案二:获利 元;
方案三:设x天进行精加工,(15-x)天进行粗加工,
,
解得: ,
获利: ,
,
选择方案三.
【考点】一元一次方程的实际应用-销售问题
【解析】【分析】方案(1)和方案(2)的获利情况可直接算出,方案三:设精加工x天,则粗加工(15-x)天,根据精加工吨数+粗加工吨数=140列出方程,解方程求出精加工和粗加工各多少天,从而求出获利.然后比较可得出答案.
22.【答案】 解:设船在静水中的平均速度为每小时x千米,则顺流速度为(x+3)千米每小时,逆流速度为(x-3)千米每小时,根据往返路程相等,列得2( x+3)=3( x-3)解得: x=15.答:船在静水中的平均速度为每小时15千米
【考点】一元一次方程的实际应用-行程问题
【解析】【分析】设船在静水中的平均速度为每小时x千米,则顺流速度为(x+3)千米每小时,逆流速度为(x-3)千米每小时,根据等量关系式:往返路程相等列出方程,解之即可.
23.【答案】 解:设乙的速度是x千米/小时,则甲的速度为(3x+1)千米/小时,
由题意得 ,
解得 x=5,
3x+1=16,
答:甲的速度为16千米/小时,乙的速度是5千米/小时.
【考点】一元一次方程的实际应用-行程问题
【解析】【分析】设乙的速度是x千米/小时,则甲的速度为(3x+1)千米/小时,根据二人行走路程之和为A、B两地路程的二倍列出方程,解方程即可.
一元一次方程
一、单选题
1.若关于x的一元一次方程2k﹣x﹣4=0的解是x=﹣3,那么k的值是( )
A. B. C. 6 D. 10
2.把方程 去分母后,正确的是( ).
A. B.
C. D.
3.B是线段AD上一动点,沿A至D的方向以 的速度运动.C是线段BD的中点. .在运动过程中,若线段AB的中点为E.则EC的长是( )
A. B. C. 或 D. 不能确定
4.一件商品按成本价提高30%后标价,再打8折(标价的80%)销售,售价为312元,设这件商品的成本价为x元,根据题意,下面所列的方程正确的是( )
A. x·30%×80%=312 B. x·30%=312×80%
C. 312×30%×80%=x D. x(1+30%)×80%=312
5.某药店经营的抗病毒药品,在市场紧缺的情况下提价100%,物价部门查处后,限定其提价的幅度只能是原价的10%,则该药品现在降价的幅度是( )
A. 45% B. 50% C. 90% D. 95%
6.阅读:关于x方程ax=b在不同的条件下解的情况如下:(1)当a≠0时,有唯一解x= ;(2)当a=0,b=0时有无数解;(3)当a=0,b≠0时无解.请你根据以上知识作答:已知关于x的方程 a= ﹣ (x﹣6)无解,则a的值是( )
A. 1 B. ﹣1 C. ±1 D. a≠1
7.甲车与乙车同时从A地出发去往B地,如图所示,折线O-A-B-C和射线OC分别是甲、乙两车行进过程中路程与时间的关系,已知甲车中途有事停留36分钟后再继续前往C地,两车同时到达C地,则下列说法:①乙车的速度为70千米/时;②甲车再次出发后的速度为100千米/时;③两车在到达B地前不会相遇;④甲车再次出发时,两车相距60千米。其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
8.在长方形 中,放入6个形状大小完全相同的小长方形,所标尺寸如图所示,则小长方形的宽 的长度为( ) cm .
A. 1 B. 1.6 C. 2 D. 2.5
9.如图,点O在直线 上,过O作射线 , ,一直角三角板的直角顶点与点O重合,边 与 重合,边 在直线 的下方.若三角板绕点O按每秒 的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线 恰好平分锐角 ,则t的值为( )
A. 5 B. 4 C. 5或23 D. 4或22
10.下列说法:
①符号相反的数互为相反数;②有理数a、b、c满足 ,且 ,则化简 的值为5;③若 是关于x的一元一次方程,则这个方程的解是 ;④若 是关于x的一元一次方程,则 ;
其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
11.如图所示,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,长的一根露出水面的长度是它的 ,短的一根露出水面的长度是它的 ,已知两根铁棒长度的和是55cm,此时木桶中水的深度是( )。
A. 25cm B. 20cm C. 30cm D. 35cm
二、填空题
12.若 是关于x的一元一次方程,则m=________.
13.已知关于 的一元一次方程 的解为 ,那么关于 的一元二次方程 的解 =________.
14.家住山脚下的小明从家出发登山游玩,他下山的速度比上山的速度快 ,他上山 到达的位置离山顶还有 ,到山顶后抄近路下山,下山路程比上山路程近 ,下山用了 ,那么小明上山的路程(到山顶)为 .
15.当x=________时,式子 与 的值互为相反数.
16.已知关于x的一元一次方程 +5=2019x+m的解为x=2018,那么关于y的一元一次方程 ﹣5=2019(5﹣y)﹣m的解为________.
17.如图,在数轴上A点表示数﹣2,B点表示数6,若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,则经过________秒,甲、乙两小球到原点的距离相等.
18.A、B两地之间的公路长108千米,小光骑自行车从A地到B地,小明骑自行车从B地到A地,两人都沿这条公路匀速前进,其中两人的速度都小于27千米/时.若同时出发3小时相遇,则经过________小时两人相距36千米.
三、解答题
19.列方程解应用题:
为参加学校运动会,七年级一班和七年级二班准备购买运动服. 下面是某服装厂给出的运动服价格表:
购买服装数(套) 1~35 36~60 61及61以上
每套服装价(元) 60 50 40
已知两班共有学生67人(每班学生人数都不超过60人),如果两班单独购买服装,每人只买一套,那么一共应付3650元. 问七年级一班和七年级二班各有学生多少人?
20.昨天老师带着我们班同学去深圳少年宫玩,我们一共去了 60人(包括老师),买门票共花了1240元.玩得可开心了!
小明:真羡慕你们,不过听说门票还是挺贵的.
小红:是的,老师票每张30元,学生票每张20元.那你能猜出我们去了几位老师,几位学生吗?
小明:去了……
根据以上的对话,你能用解方程的知识帮助小明回答小红的提问吗?
21.某地的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元;经粗加工后销售,每吨利润4000元;经精加工后销售,每吨利润7000元.当地一家公司现有这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果对蔬菜进行精加工,每天可加工6吨;但每天两种方式不能同时进行.受季节等条件的限制,必须用15天时间将这批蔬菜
全部销售或加工完毕.为此,公司研制了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能地对蔬菜进行精加工,没来得及加工的蔬菜,在市场上直接出售;
方案三:将一部分蔬菜进行精加工,其余蔬菜进行粗加工,并刚好15天完成.
如果你是公司经理,你会选择哪一种方案,请说说理由.
22.一艘船从甲码头到乙码头顺流而行,用了2小时,从乙码头返回甲码头逆流而行,用了3小时,已知水流的速度是每小时3千米, 求船在静水中的平均速度.
23.甲、乙二人同时从相距 千米的A地去B地,甲骑车,乙步行.甲每小时的速度比乙每小时的速度的3倍多1千米,甲达到B地后停留45分,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3小时,求两人的速度各是多少?
答案解析部分
一、单选题
1.【答案】 A
【考点】一元一次方程的解
【解析】【解答】解:∵关于x的一元一次方程2k﹣x﹣4=0的解是x=﹣3,
∴2k+3﹣4=0,
解得:k= ,
故答案为:A.
【分析】将x=﹣3代入2k﹣x﹣4=0中,即可求出k值.
2.【答案】 D
【考点】解含分数系数的一元一次方程
【解析】【解答】去分母得:3x-2(x-1)=6,
故答案为:D.
【分析】将方程两边都乘以6去分母计算即可。
3.【答案】 B
【考点】线段的中点,一元一次方程的实际应用-行程问题
【解析】【解答】设运动时间为t,
则AB=2t,BD=10-2t,
∵C是线段BD的中点,E为线段AB的中点,
∴EB= =t,BC= =5-t,
∴EC=EB+BC=t+5-t=5cm,
故答案为:B.
【分析】根据线段中点的性质,做出线段AD,按要求标出各点大致位置,列出EB,BC的表达式,即可求出线段EC.
4.【答案】 D
【考点】一元一次方程的实际应用-销售问题
【解析】【解答】设这件商品的成本价为x元,成本价提高30%后的标价为x(1+30%),再打8折的售价表示为x(1+30%)×80%,又因售价为312元,
列方程为:x(1+30%)×80%=312.
故答案为:D.
【分析】按成本价的30%标价,则标价为成本价的(1+30%),打八折即用标价×80%,即可得到售价,进而列出方程.
5.【答案】 A
【考点】一元一次方程的实际应用-销售问题
【解析】【解答】解:设药品的原价为a元,药品现在降价x,则根据题意可得:a(1+100%)(1-x)=a(1+10%),
解得x=45%,
故答案为:A.
【分析】设药品的原价为a元,药品现在降价x,根据提价后的价格×(1-x)=降价后的价格,列出方程,解之即可.
6.【答案】 A
【考点】解一元一次方程
【解析】【解答】要把原方程变形化简,去分母得:2ax=3x﹣(x﹣6),
去括号得:2ax=2x+6,
移项,合并得,x= ,
因为无解,所以a﹣1=0,即a=1.
故答案为:A.
【分析】对方程去分母、去括号、移项、合并同类项进行求解,再根据方程无解得到关于a的方程,求解可得a的值.
7.【答案】 C
【考点】一元一次方程的实际应用-行程问题
【解析】【解答】解:① 、由图可知: V乙=3004=75 千米/时 ,故 ① 不正确;
② 、由图可知:甲车再次出发的速度,V甲=(300-60)(4-1.6)=100千米/时,故 ②正确;
③ 、 由图可知:两车在到达B地前不会相遇 ,故 ③正确;
④ 、 由图和①可知: 点B的时间=1+3660=1.6小时;V乙=75 千米/时,S乙=75 1.6=120千米, 甲车再次出发时, 两车之间的距 离=120-60=60千米,故 ④正确.
【分析】由图可知:总路程是300千米,乙车一直在匀速行驶,乙车用时4小时,甲车前一个小时匀速行驶,休息了36分钟(3660=0.6小时),再次提速匀速行驶,在4小时的时候甲乙两车同时到达目的地,即甲乙两车在目的地相遇.
8.【答案】 C
【考点】一元一次方程的实际应用-几何问题
【解析】【解答】解:设AE=xcm,
依题意,得:6+2x=x+(14 3x),
解得:x=2
故答案为:C.
【分析】设AE=xcm,得出大长方形的宽为(6+2x)cm,小长方形的长为(14-3x)cm,从而得出大长方形的宽为(x+14-3x)cm,根据用两个不同的式子表示同一个量,则这两个式子应该相等,从而列出方程,解方程求出x的值,即可求解.
9.【答案】 C
【考点】角的运算,一元一次方程的实际应用-几何问题
【解析】【解答】解:∵ ,
∴ ,
①如图,
当 的反向延长线恰好平分锐角 时,
∴ ,
此时,三角板旋转的角度为 ,
∴ ;
②如图,
当 在 的内部时,
∴∠CON= ∠AOC=40°,
∴三角板旋转的角度为90°+100°+40°=230°,
∴ ;
∴t的值为:5或23.
故答案为: C .
【分析】先求出 ,再分类讨论,进行计算求解即可。
10.【答案】 D
【考点】相反数及有理数的相反数,绝对值及有理数的绝对值,一元一次方程的定义
【解析】【解答】解:仅仅只有符号不同的两个数互为相反数,故①错误;
由 ,且 ,
所以:
< < <
故②错误;
是关于x的一元一次方程,
或 ( )或 ,
或 或
或
当 时,原方程为:
当 时,原方程化为:
,不合题意舍去,
当 时,原方程化为:
综上:方程的解为: 或 故③错误;
是关于x的一元一次方程,
,
故④正确;
故答案为:D
【分析】
11.【答案】 B
【考点】一元一次方程的实际应用-几何问题
【解析】【解答】解:设木桶中水的深度为h,由题意有
整理得:
解得:h=20
故答案为:B
【分析】根据题意长的铁棒在水里的长度为它的 , 所以长的铁棒的长度为 , 短的铁棒在水里的长度为它的 , 所以短的铁棒的长度为 , 根据两根铁棒长度的和是55cm列方程即可得到答案.
二、填空题
12.【答案】 1
【考点】一元一次方程的定义
【解析】【解答】∵ 是关于x的一元一次方程,
∴2m-1=1
解得m=1
故填:1.
【分析】只含有一个未知数,且未知数的次数是1的整式方程,叫做一元一次方程,据此解答即可.
13.【答案】 -1
【考点】一元一次方程的解
【解析】【解答】解:根据题意可得:
对原方程进行变形:
,
,
,
再把 代入上式得出: ,
故答案为: .
【分析】对原方程进行变形可以得出一个等式: ,此时 ,与所求方程进行比较可得出结果.
14.【答案】 5
【考点】一元一次方程的实际应用-行程问题
【解析】【解答】解:设小明上山的速度为xkm/h,
根据题意得:2x+1=(x+1)+2,
解这个方程得:x=2km/h,
经检验符合题意,
2x+1=4+1=5km,
答:小明上山的路程为5km,
故答案为:5.
【分析】先求出2x+1=(x+1)+2,再解方程求解即可。
15.【答案】
【考点】相反数及有理数的相反数,解含分数系数的一元一次方程
【解析】【解答】由题意得: ,去分母得:2(2x+5)+3(x+11)+12x=0,去括号得:4x+10+3x+33+12x=0,移项、合并同类项得:19x=﹣43,系数化1得:x= .故答案为 .
【分析】先根据互为相反数的和为0列出方程 , 然后再根据解方程的一般步骤①两边同时乘以各分母的最小公倍数去分母;②根据乘法的分配律去括号(不要漏乘);③移项(注意改变符号);④ 合并同类项;⑤系数化为1解方程即可.
16.【答案】 2023
【考点】一元一次方程的解
【解析】【解答】解:根据题意得:
方程 可整理得: ,
则该方程的解为x=2018,
方程 可整理得: ,
令n=5﹣y,
则原方程可整理得: ,
则n=﹣2018,
即5﹣y=﹣2018,
解得:y=2023,
故答案为:2023.
【分析】将方程整理可得 , 则该方程的解为x=2018;将关于y的方程整理为 , 令n=5﹣y,可得出 , 从而可得5﹣y=n﹣2018,求出y值即可.
17.【答案】 或8
【考点】数轴及有理数在数轴上的表示,一元一次方程的实际应用-行程问题
【解析】【解答】解:设经过t秒,甲、乙两小球到原点的距离相等.
∵甲球运动的路程为:1 t=t,OA=2,
∴甲球与原点的距离为:t+2;
乙球到原点的距离分两种情况:当0<t≤3时,乙球从点B处开始向左运动,一直到原点O,
∵OB=6,乙球运动的路程为:2 t=2t,乙到原点的距离:6﹣2t(0≤t≤3);
当t>3时,乙球从原点O处开始一直向右运动,此时乙球到原点的距离为:2t﹣6 (t>3).
分两种情况:
①当0<t≤3时,得t+2=6﹣2t,解得t= ;
当t>3时,得t+2=2t﹣6,解得t=8.
故当t= 或8秒时,甲乙两小球到原点的距离相等.
故答案为 或8.
【分析】设经过t秒,甲、乙两小球到原点的距离相等.分两种情况:①0<t≤3,②t>3,根据甲、乙两小球到原点的距离相等列出关于t的方程,解方程即可.
18.【答案】 2或4
【考点】一元一次方程的实际应用-行程问题
【解析】【解答】设经过x小时两人相距36千米,
∵同时出发3小时相遇,
∴可得两人的速度和为: 千米/小时,
①两人相遇前相距36千米,
解得: ;
②两人相遇后相距36千米,
解得: ;
综上,经过2小时或4小时两人相距36千米,
故答案为:2或4.
【分析】先求出两人的速度和为36千米/小时,再分类讨论,列方程求解即可。
三、解答题
19.【答案】 解:∵
∴所以一定有一个班的人数大于35人.
设大于35人的班有学生x人,则另一班有学生(67-x)人,
依题意得
答:七年级一班有37人,七年级二班有30人;或者七年级一班有30人,七年级二班有37人.
【考点】一元一次方程的实际应用-销售问题
【解析】【分析】首先根据题中表格数据得出有一个班的人数大于35人,接着设大于35人的班有学生x人,根据等量关系列出方程,求解即可.
20.【答案】 解:设去了x名学生,(60-x)名老师,依题意得:
30(60-x)+20x=1240,
解之得:x=56,
所以老师: 60-56=4名,
答:共去了4位老师,56位学生.
【考点】一元一次方程的实际应用-销售问题
【解析】【分析】设去了x名学生,(60-x)名老师,根据买门票共花了1240元,列方程进行求解即可得.
21.【答案】 解:方案一:获利 元,
方案二:获利 元;
方案三:设x天进行精加工,(15-x)天进行粗加工,
,
解得: ,
获利: ,
,
选择方案三.
【考点】一元一次方程的实际应用-销售问题
【解析】【分析】方案(1)和方案(2)的获利情况可直接算出,方案三:设精加工x天,则粗加工(15-x)天,根据精加工吨数+粗加工吨数=140列出方程,解方程求出精加工和粗加工各多少天,从而求出获利.然后比较可得出答案.
22.【答案】 解:设船在静水中的平均速度为每小时x千米,则顺流速度为(x+3)千米每小时,逆流速度为(x-3)千米每小时,根据往返路程相等,列得2( x+3)=3( x-3)解得: x=15.答:船在静水中的平均速度为每小时15千米
【考点】一元一次方程的实际应用-行程问题
【解析】【分析】设船在静水中的平均速度为每小时x千米,则顺流速度为(x+3)千米每小时,逆流速度为(x-3)千米每小时,根据等量关系式:往返路程相等列出方程,解之即可.
23.【答案】 解:设乙的速度是x千米/小时,则甲的速度为(3x+1)千米/小时,
由题意得 ,
解得 x=5,
3x+1=16,
答:甲的速度为16千米/小时,乙的速度是5千米/小时.
【考点】一元一次方程的实际应用-行程问题
【解析】【分析】设乙的速度是x千米/小时,则甲的速度为(3x+1)千米/小时,根据二人行走路程之和为A、B两地路程的二倍列出方程,解方程即可.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
