人教版七年级上册数学2.2整式的加减的应用同步练习(word版含答案)
文档属性
| 名称 | 人教版七年级上册数学2.2整式的加减的应用同步练习(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 514.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 21:25:26 | ||
图片预览



文档简介
人教版七年级上册数学2.2整式的加减的应用同步练习
一、单选题
1.一个长方形的长是宽的1.5倍.如果宽为x m,那么这个长方形的周长是( )
A.(1.5x+1) m B.2.5x m C.(3x+2) m D.5x m
2.某年级组织学生乘车赴革命教育基地参观,若全部租用8座客车x辆,则余下6人无座位;若全部租用12座客车,则可少租用1辆,此时最后一辆车人未满坐,则乘坐最后一辆12座客车的人数是( )
A.18-4x B.6-4x C.30-4x D.18-8x
3.设A=3x2﹣3x+5,B=2x2﹣3x﹣2,若x取任意实数,则A与B的大小关系为( )
A.A>B B.A<B C.A=B D.无法比较
4.如图,表示这个图形面积的代数式是( )
A. B. C. D.
5.在一张普通的月历当中,一个日期与它的上下、左右四个日期的数字和一定是下列哪个数的倍数?( )
A.4 B.5 C.6 D.7
6.已知两个完全相同大长方形,长为a,各放入四个完全一样的白色小长方形后,得到图(1)、图(2),那么,图(1)阴影部分的周长与图(2)阴影部分的周长的差是( )
A.a B. C. D.
7.如图,一个长方形是由四块小长方形拼成(四块小长方形放置时既不重叠,也没有空隙),其中②和③两块长方形的形状大小完全相同,如果要求出①和④两块长方形的周长之差,则只要知道哪条线段的长( )
A. B. C. D.
8.某商店在甲批发市场以m元/包的价格购进了30包茶叶,又在乙批发市场以n元/包(m<n)的价格购进了相同的50包茶叶,并以元/包的价格将所购茶叶全部售出,那么该商家最终的盈亏情况是( )
A.盈利了 B.亏损了
C.既不盈利也不亏损 D.无法确定盈亏情况
二、填空题
9.小明同学从商家以每顶4元的价格购进了顶帽子,以每顶5元的价格售出了顶帽子,剩余的以每顶2元的价格退回商家,则小明卖帽子的收入为__________元.
10.某超市搞促销活动,对一种软皮本的销售方式是买一赠一,即买一本软皮本赠送一支铅笔,这种软皮本每本定价2元,铅笔每支定价0.3元,若小明的爸爸买回软皮本x本,铅笔y支,则需要付______________元钱
11.如图,两个正方形边长分别为a、b,如果a2+b2=300,ab=12,则阴影部分的面积为______.
12.矩形中,横向阴影部分是长方形,另一部分是平行四边形,依照图中标注的据,图中空白部分的面积为___________.
13.一个长方形的一边长米,另一边比它短米,则这个长方形的周长为________.
14.,,,,,,…是一列数,已知,,且任意三个相邻的数之和为18,则________.
15.已知某长方形的长为,它的宽比长短,则这个长方形的宽是_____.
16.某同学在做计算时,误将看成了,求得的结果是 已知 ,则=___
三、解答题
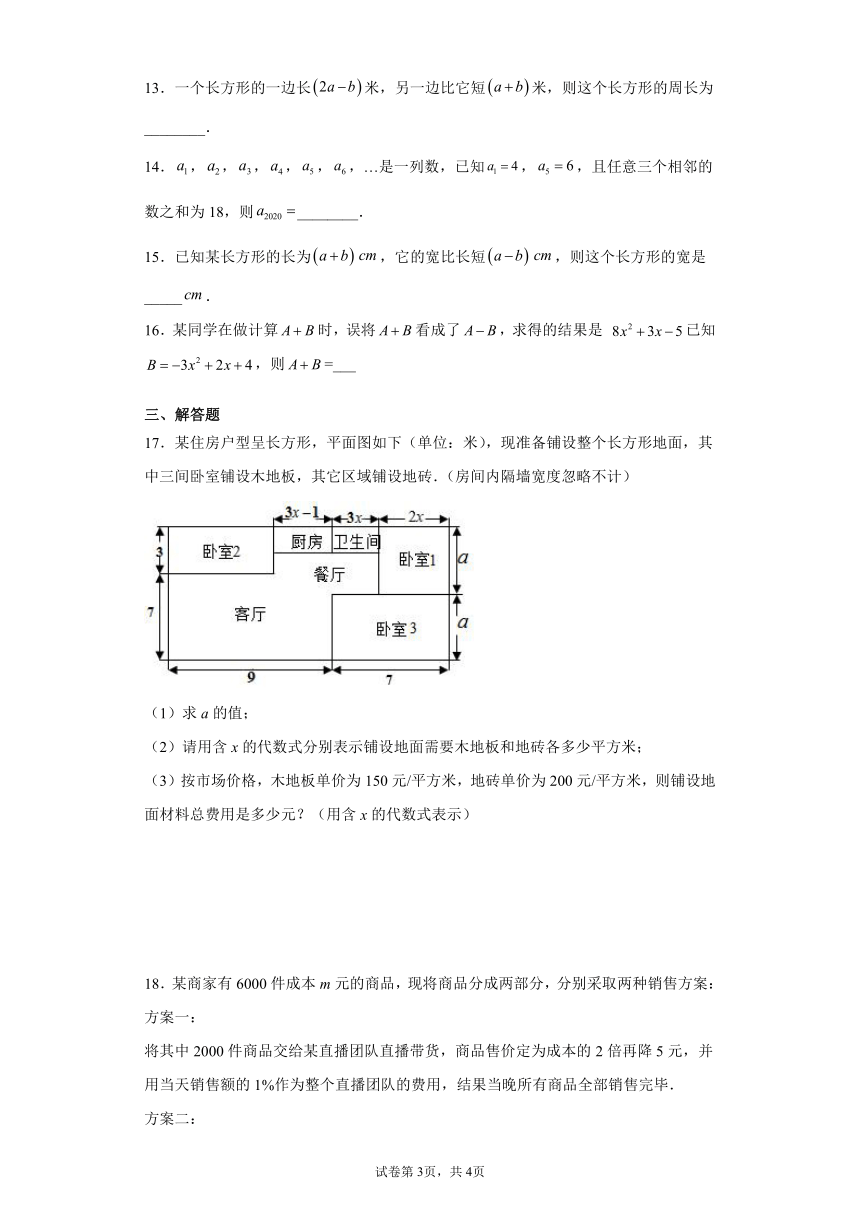
17.某住房户型呈长方形,平面图如下(单位:米),现准备铺设整个长方形地面,其中三间卧室铺设木地板,其它区域铺设地砖.(房间内隔墙宽度忽略不计)
(1)求a的值;
(2)请用含x的代数式分别表示铺设地面需要木地板和地砖各多少平方米;
(3)按市场价格,木地板单价为150元/平方米,地砖单价为200元/平方米,则铺设地面材料总费用是多少元?(用含x的代数式表示)
18.某商家有6000件成本m元的商品,现将商品分成两部分,分别采取两种销售方案:
方案一:
将其中2000件商品交给某直播团队直播带货,商品售价定为成本的2倍再降5元,并用当天销售额的1%作为整个直播团队的费用,结果当晚所有商品全部销售完毕.
方案二:
将剩下的商品打折销售,售价定为成本的2.5倍,第一次打八折,售出1000件;第二次再打八折,剩下商品被一抢而空.
(1)用含m的代数式表示方案一中直播团队的费用为 元;
(2)用含m的代数式表示方案二的总销售额;
(3)用含m的代数式表示商家两种方案销售后的总盈利.
19.如图是一个工件的横断面及其尺寸.(单位:).
(1)用含,的式子表示它的面积;
(2)当,时,求的值.(结果保留)
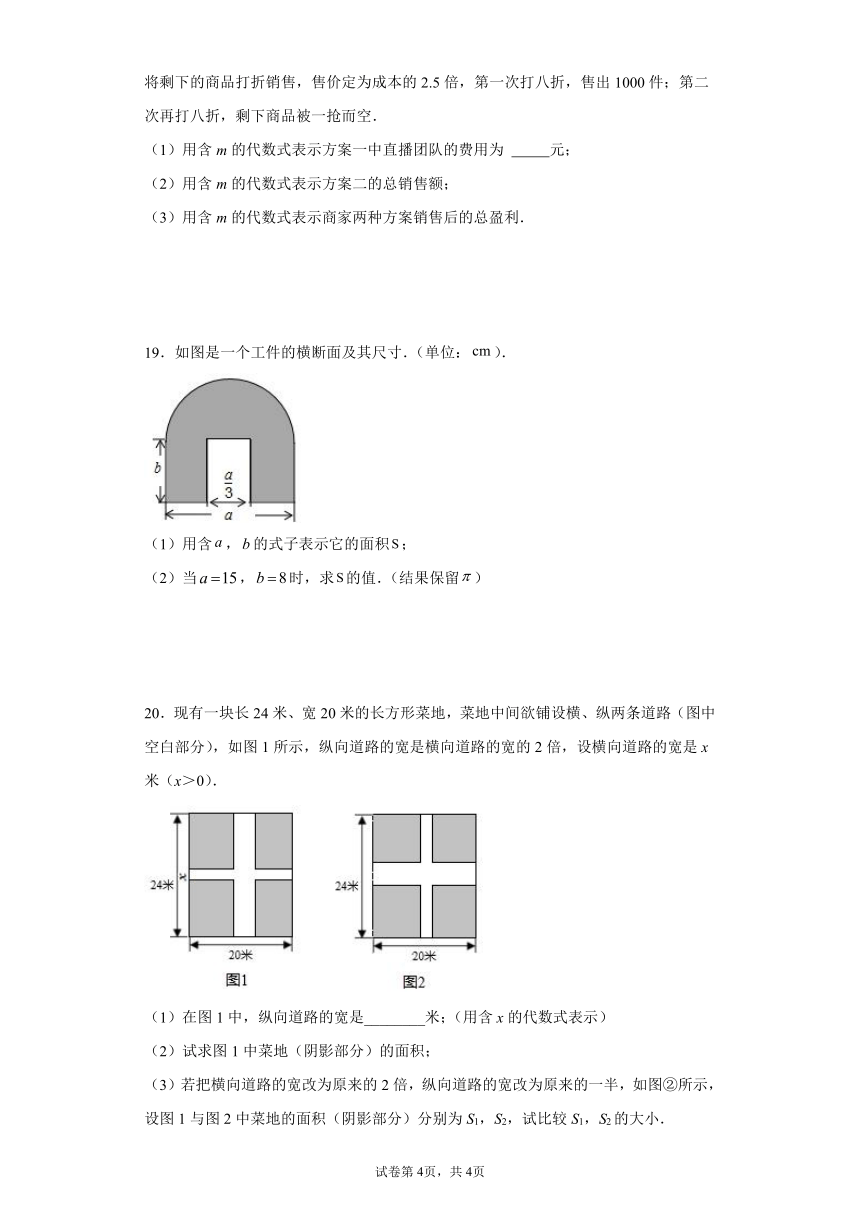
20.现有一块长24米、宽20米的长方形菜地,菜地中间欲铺设横、纵两条道路(图中空白部分),如图1所示,纵向道路的宽是横向道路的宽的2倍,设横向道路的宽是x米(x>0).
(1)在图1中,纵向道路的宽是________米;(用含x的代数式表示)
(2)试求图1中菜地(阴影部分)的面积;
(3)若把横向道路的宽改为原来的2倍,纵向道路的宽改为原来的一半,如图②所示,设图1与图2中菜地的面积(阴影部分)分别为S1,S2,试比较S1,S2的大小.
参考答案
1.D
【分析】
根据已知条件长方形的长是宽的1.5倍,宽为x m,则可用代数式表示出该长方形的长,进而利用长方形的周长公式计算出该长方形的周长.
【详解】
∵该长方形的长是宽的1.5倍,宽为x m,
∴该长方形的长为:,
∴该长方形的周长为:,
故选:D
【点睛】
本题考查了列代数式、整式的加减和长方形周长的计算等知识点,解答本题的关键是熟练掌握并运用以上知识点.
2.C
【分析】
先求出总人数,然后根据整式的加减法则求解即可.
【详解】
解:∵全部租用8座的车x辆,则余下6人无座位,
∴一共有(8x+6)人,
∵全部租用12座的车(x﹣1)辆,最后一辆车人未满坐,
∴乘坐最后一辆12座的车的人数是(8x+6)﹣12(x﹣2)=8x+6﹣12x+24=30﹣4x.
故选:C.
【点睛】
本题考查列代数式,理解题意,根据所给信息找到等量关系,列出正确的代数式是解题的关键.
3.A
【分析】
先根据整式的加减运算法则计算的值,再根据偶次方的非负性即可得出答案.
【详解】
解:
,
则,
故选:A.
【点睛】
本题考查了整式加减的应用,熟练掌握整式的加减法则是解题关键.
4.C
【分析】
把图形补成一个大矩形,则很容易表达出阴影部分面积.
【详解】
解:把图形补成一个大矩形,则阴影部分面积=ab﹣(a﹣c)(b﹣d)=ab﹣[ab﹣ad﹣c(b﹣d)]=ab﹣ab+ad+c(b﹣d)=ad+cb-cd.
故选C.
【点睛】
此题考查整式的加减,解题的关键是把图形补成一个大矩形,从而求出阴影部分的面积.
5.A
【分析】
根据题意表示出所有的数,相加,根据结果即可判断.
【详解】
解:设这个数为x,则上面的数为x-7,下面的数为x+7,左边的数为x-1,右边的数为x+1,
∴四个数字的和为x-7+x+7+x-1+x+1=4x,
∴四个数字的和一定是4的倍数,
故选A.
【点睛】
此题考查了列代数式;解题关键是要读懂题目的意思,理解月历的特征,根据题目给出的条件,列出代数式.
6.A
【分析】
设小长方形的长为x,宽为y,大长方形宽为b,表示出x、y、a、b之间的关系,然后求出阴影部分周长之差即可.
【详解】
解:设图中小长方形的长为x,宽为y,大长方形的宽为b,
根据题意,得:x+2y=a、x=2y,
则4y=a,
图(1)中阴影部分周长为2b+2(a-x)+2x=2a+2b,图(2)中阴影部分的周长为2(a+b-2y)=2a+2b-4y,
图(1)阴影部分周长与图(2)阴影部分周长之差为:(2a+2b)-(2a+2b-4y)=4y=a,
故选:A.
【点睛】
此题考查了整式的加减,以及列代数式,熟练掌握运算法则是解本题的关键.
7.B
【分析】
设标号为②和③的两块长方形的长为x、宽为y,根据题意表示出标号为①和④的周长,并作差即可求解.
【详解】
设标号为②和③的两块长方形的长为x、宽为y,
根据题意,标号为①的长方形的周长为,标号为④的长方形周长为,
所以标号为①和④两块长方形的周长之差为:,
故只要知道线段的长度.
故选:B.
【点睛】
本题主要考查整式加减的应用,能够表示出标号为①和④的周长是关键.
8.A
【分析】
分别用含m和n的式子表示出总进价和总收入,然后用总收入减去总进价即为利润,根据结果与0的大小比较,即可得出答案.
【详解】
解:由题意得:
总进价为:(30m+50n)元,共进了30+50=80(包),
∵商家以每包元的价格卖出,
∴总收入为:×80=(40m+40n)元,
∴利润为:(40m+40n)(30m+50n)
=40m+40n30m50n
=10m10n
=10(mn),
∵m>n,
∴10(mn)>0,
∴盈利了.
故选:A.
【点睛】
本题考查了列代数式在成本利润问题中的应用,明确成本利润问题的基本数量关系是解题的关键.
9.##
【分析】
根据题意,可得售出的帽子的费用加上退回商家的费用减去购进帽子的费用,即可求解.
【详解】
解: .
故答案为: .
【点睛】
本题主要考查了整式的加减的应用,明确题意,准确列出代数式是解题的关键.
10.或
【分析】
根据题意列式计算即可得.
【详解】
解:当时:(元);
当x故答案为:或.
【点睛】
本题考查了代数式,解题的关键是找出题意中的关系列出代数式.
11.144
【分析】
由图形可得,阴影部分的面积等于整个图形面积减去空白部分的面积,即可求解.
【详解】
解:由图形可得,阴影部分的面积等于整个图形面积减去空白部分的面积,
∵,
∴
故答案为:144.
【点睛】
此题考查了不规则图形的面积计算,解题的关键是不规则图形的面积转化为规则图形的面积,运用转化的思想.
12.ab-bc-ac+c2
【分析】
先求出矩形的面积(ab),再求出阴影部分的面积(ac和bc),两块交叉的部分面积是c2,根据图形求出即可.
【详解】
解:∵矩形ABCD的面积是ab,
阴影部分的面积是:ac+bc-c2,
∴图中空白部分的面积是:ab-(ac+bc-c2)=ab-bc-ac+c2.
故答案为:ab-bc-ac+c2.
【点睛】
本题考查了矩形的性质,平行四边形的性质,整式的运算的应用,注意:两块阴影部分的交叉处的面积是c2,题目比较好,但是一道比较容易出错的题目.
13.(6a-6b)米
【分析】
直接利用整式的加减运算法则计算得出答案.
【详解】
解:∵长方形的一边长为(2a-b)米,另一边比它短(a+b)米,
∴另一边为:2a-b-a b=a-2b,
∴这个正方形的周长是:2(2a-b+a-2b)=6a-6b.
故答案为:(6a-6b)米.
【点睛】
此题主要考查了整式的加减运算,正确掌握相关运算法则是解题关键.
14.4
【分析】
根据题意,可以得到,,,,,,从而可以发现题目中的数列以4,6,8依次循环出现,从而可以得到第2020个数的值.
【详解】
解:∵任意三个数的和为18,
∴①,
②,
③,
①+③-②得
,
∴,
∵,,
∴,
∴,
,
即,,,,,,
…,
∴,,,,,…的值三个一组循环,
∵,
∴.
故答案为:4.
【点睛】
本题考查数字的变化类,解答本题的关键是明确题意,发现数字的变化特点,写出第2020个数a2020的值.
15.
【分析】
根据题意列出算式,然后根据整式的运算法则即可求出答案.
【详解】
解:由题意可知宽为:.
故答案为:.
【点睛】
本题考查了整式的运算,熟练运用整式的运算法则是解题的关键.
16..
【分析】
根据题意可得A﹣B=,将代入其中求出A的代数式,然后再根据A+B计算即可.
【详解】
解:,,
,
即,
,
故答案为:.
【点睛】
本题主要考查了整式加减运算的实际运用,熟练掌握运算法则是解题关键.
17.(1);(2)木地板(-14x+86)平方米,地砖(14x+74)平方米;(3)总费用为(700x+27700)元.
【分析】
(1)根据长方形的对边相等可得2a=3+7,即可求出a的值;
(2)根据三间卧室铺设木地板,其它区域铺设地砖,可知将三间卧室的面积的和为木地板的面积,用长方形的面积-三间卧室的面积,所得的差为地砖的面积;
(3)根据所铺设面积和每种材料的单价,求出所需的费用即可.
【详解】
解:(1)根据题意得,
解得;
(2)铺设地面需要木地板:平方米;
铺设地面需要地砖:平方米;
(3)总费用=地砖费用+木地板费用
=,
则铺设地面的总费用为(700x+27700)元.
【点睛】
本题考查了列代数式,一元一次方程的应用.长方形的面积,分别求出铺设地面需要木地板与地砖的面积是解题的关键.
18.(1);(2);(3)
【分析】
(1)根据售价定为成本的2倍再降5元,并用当天销售额的1%作为整个直播团队的费用,列式即可;
(2)直接根据方案二的方式列式即可;
(3)根据总盈利=总销售额-总成本-直播团队的费用.
【详解】
解:(1)由题意可得:
直播团队的费用为:(元),
故答案为:;
(2)根据题意得:
方案二总销售额:
=,
故方案二总销售额为;
(3)方案一、方案二的总销售额=,
直播团队的费用为:元;
商品总成本为:,
总盈利=.
【点睛】
本题考查了列代数式,读懂题意,明确题中数量关系是解本题的关键.
19.(1);(2)
【分析】
(1)把图形分成半圆,一个大长方形和一个小长方形,由割补法即可求出面积;
(2)把,代入(1)中的式子即可得出答案.
【详解】
(1)由题可得:;
(2)当, 时,.
【点睛】
本题考查列代数式以及整式的运算,根据题意掌握用割补法表示面积是解题的关键.
20.(1);(2)平方米;(3)
【分析】
(1)根据纵向道路的宽是横向道路的宽的2倍即可求解;
(2)根据题意,由菜地的面积长方形的面积-道路的面积求解即可;
(3)根据菜地的面积长方形的面积-道路的面积分别求出、,再作差比较即可.
【详解】
解:(1)横向道路的宽是米,且纵向道路的宽是横向道路的宽的2倍,
纵向道路的宽是米,
故答案为:;
(2)由题意得:图1中菜地的面积为
平方米,
答:图1中菜地(阴影部分)的面积为平方米;
(3)由题意:图1中菜地的面积,
图2中横向道路的宽为米,纵向道路的宽为米,
∴图2中菜地的面积
平方米,
,
,
∴,
.
【点睛】
本题考查了列代数式、整式加减的应用、长方形的面积,正确表示出菜地的面积是解答的关键.
试卷第4页,共4页
试卷第3页,共4页
一、单选题
1.一个长方形的长是宽的1.5倍.如果宽为x m,那么这个长方形的周长是( )
A.(1.5x+1) m B.2.5x m C.(3x+2) m D.5x m
2.某年级组织学生乘车赴革命教育基地参观,若全部租用8座客车x辆,则余下6人无座位;若全部租用12座客车,则可少租用1辆,此时最后一辆车人未满坐,则乘坐最后一辆12座客车的人数是( )
A.18-4x B.6-4x C.30-4x D.18-8x
3.设A=3x2﹣3x+5,B=2x2﹣3x﹣2,若x取任意实数,则A与B的大小关系为( )
A.A>B B.A<B C.A=B D.无法比较
4.如图,表示这个图形面积的代数式是( )
A. B. C. D.
5.在一张普通的月历当中,一个日期与它的上下、左右四个日期的数字和一定是下列哪个数的倍数?( )
A.4 B.5 C.6 D.7
6.已知两个完全相同大长方形,长为a,各放入四个完全一样的白色小长方形后,得到图(1)、图(2),那么,图(1)阴影部分的周长与图(2)阴影部分的周长的差是( )
A.a B. C. D.
7.如图,一个长方形是由四块小长方形拼成(四块小长方形放置时既不重叠,也没有空隙),其中②和③两块长方形的形状大小完全相同,如果要求出①和④两块长方形的周长之差,则只要知道哪条线段的长( )
A. B. C. D.
8.某商店在甲批发市场以m元/包的价格购进了30包茶叶,又在乙批发市场以n元/包(m<n)的价格购进了相同的50包茶叶,并以元/包的价格将所购茶叶全部售出,那么该商家最终的盈亏情况是( )
A.盈利了 B.亏损了
C.既不盈利也不亏损 D.无法确定盈亏情况
二、填空题
9.小明同学从商家以每顶4元的价格购进了顶帽子,以每顶5元的价格售出了顶帽子,剩余的以每顶2元的价格退回商家,则小明卖帽子的收入为__________元.
10.某超市搞促销活动,对一种软皮本的销售方式是买一赠一,即买一本软皮本赠送一支铅笔,这种软皮本每本定价2元,铅笔每支定价0.3元,若小明的爸爸买回软皮本x本,铅笔y支,则需要付______________元钱
11.如图,两个正方形边长分别为a、b,如果a2+b2=300,ab=12,则阴影部分的面积为______.
12.矩形中,横向阴影部分是长方形,另一部分是平行四边形,依照图中标注的据,图中空白部分的面积为___________.
13.一个长方形的一边长米,另一边比它短米,则这个长方形的周长为________.
14.,,,,,,…是一列数,已知,,且任意三个相邻的数之和为18,则________.
15.已知某长方形的长为,它的宽比长短,则这个长方形的宽是_____.
16.某同学在做计算时,误将看成了,求得的结果是 已知 ,则=___
三、解答题
17.某住房户型呈长方形,平面图如下(单位:米),现准备铺设整个长方形地面,其中三间卧室铺设木地板,其它区域铺设地砖.(房间内隔墙宽度忽略不计)
(1)求a的值;
(2)请用含x的代数式分别表示铺设地面需要木地板和地砖各多少平方米;
(3)按市场价格,木地板单价为150元/平方米,地砖单价为200元/平方米,则铺设地面材料总费用是多少元?(用含x的代数式表示)
18.某商家有6000件成本m元的商品,现将商品分成两部分,分别采取两种销售方案:
方案一:
将其中2000件商品交给某直播团队直播带货,商品售价定为成本的2倍再降5元,并用当天销售额的1%作为整个直播团队的费用,结果当晚所有商品全部销售完毕.
方案二:
将剩下的商品打折销售,售价定为成本的2.5倍,第一次打八折,售出1000件;第二次再打八折,剩下商品被一抢而空.
(1)用含m的代数式表示方案一中直播团队的费用为 元;
(2)用含m的代数式表示方案二的总销售额;
(3)用含m的代数式表示商家两种方案销售后的总盈利.
19.如图是一个工件的横断面及其尺寸.(单位:).
(1)用含,的式子表示它的面积;
(2)当,时,求的值.(结果保留)
20.现有一块长24米、宽20米的长方形菜地,菜地中间欲铺设横、纵两条道路(图中空白部分),如图1所示,纵向道路的宽是横向道路的宽的2倍,设横向道路的宽是x米(x>0).
(1)在图1中,纵向道路的宽是________米;(用含x的代数式表示)
(2)试求图1中菜地(阴影部分)的面积;
(3)若把横向道路的宽改为原来的2倍,纵向道路的宽改为原来的一半,如图②所示,设图1与图2中菜地的面积(阴影部分)分别为S1,S2,试比较S1,S2的大小.
参考答案
1.D
【分析】
根据已知条件长方形的长是宽的1.5倍,宽为x m,则可用代数式表示出该长方形的长,进而利用长方形的周长公式计算出该长方形的周长.
【详解】
∵该长方形的长是宽的1.5倍,宽为x m,
∴该长方形的长为:,
∴该长方形的周长为:,
故选:D
【点睛】
本题考查了列代数式、整式的加减和长方形周长的计算等知识点,解答本题的关键是熟练掌握并运用以上知识点.
2.C
【分析】
先求出总人数,然后根据整式的加减法则求解即可.
【详解】
解:∵全部租用8座的车x辆,则余下6人无座位,
∴一共有(8x+6)人,
∵全部租用12座的车(x﹣1)辆,最后一辆车人未满坐,
∴乘坐最后一辆12座的车的人数是(8x+6)﹣12(x﹣2)=8x+6﹣12x+24=30﹣4x.
故选:C.
【点睛】
本题考查列代数式,理解题意,根据所给信息找到等量关系,列出正确的代数式是解题的关键.
3.A
【分析】
先根据整式的加减运算法则计算的值,再根据偶次方的非负性即可得出答案.
【详解】
解:
,
则,
故选:A.
【点睛】
本题考查了整式加减的应用,熟练掌握整式的加减法则是解题关键.
4.C
【分析】
把图形补成一个大矩形,则很容易表达出阴影部分面积.
【详解】
解:把图形补成一个大矩形,则阴影部分面积=ab﹣(a﹣c)(b﹣d)=ab﹣[ab﹣ad﹣c(b﹣d)]=ab﹣ab+ad+c(b﹣d)=ad+cb-cd.
故选C.
【点睛】
此题考查整式的加减,解题的关键是把图形补成一个大矩形,从而求出阴影部分的面积.
5.A
【分析】
根据题意表示出所有的数,相加,根据结果即可判断.
【详解】
解:设这个数为x,则上面的数为x-7,下面的数为x+7,左边的数为x-1,右边的数为x+1,
∴四个数字的和为x-7+x+7+x-1+x+1=4x,
∴四个数字的和一定是4的倍数,
故选A.
【点睛】
此题考查了列代数式;解题关键是要读懂题目的意思,理解月历的特征,根据题目给出的条件,列出代数式.
6.A
【分析】
设小长方形的长为x,宽为y,大长方形宽为b,表示出x、y、a、b之间的关系,然后求出阴影部分周长之差即可.
【详解】
解:设图中小长方形的长为x,宽为y,大长方形的宽为b,
根据题意,得:x+2y=a、x=2y,
则4y=a,
图(1)中阴影部分周长为2b+2(a-x)+2x=2a+2b,图(2)中阴影部分的周长为2(a+b-2y)=2a+2b-4y,
图(1)阴影部分周长与图(2)阴影部分周长之差为:(2a+2b)-(2a+2b-4y)=4y=a,
故选:A.
【点睛】
此题考查了整式的加减,以及列代数式,熟练掌握运算法则是解本题的关键.
7.B
【分析】
设标号为②和③的两块长方形的长为x、宽为y,根据题意表示出标号为①和④的周长,并作差即可求解.
【详解】
设标号为②和③的两块长方形的长为x、宽为y,
根据题意,标号为①的长方形的周长为,标号为④的长方形周长为,
所以标号为①和④两块长方形的周长之差为:,
故只要知道线段的长度.
故选:B.
【点睛】
本题主要考查整式加减的应用,能够表示出标号为①和④的周长是关键.
8.A
【分析】
分别用含m和n的式子表示出总进价和总收入,然后用总收入减去总进价即为利润,根据结果与0的大小比较,即可得出答案.
【详解】
解:由题意得:
总进价为:(30m+50n)元,共进了30+50=80(包),
∵商家以每包元的价格卖出,
∴总收入为:×80=(40m+40n)元,
∴利润为:(40m+40n)(30m+50n)
=40m+40n30m50n
=10m10n
=10(mn),
∵m>n,
∴10(mn)>0,
∴盈利了.
故选:A.
【点睛】
本题考查了列代数式在成本利润问题中的应用,明确成本利润问题的基本数量关系是解题的关键.
9.##
【分析】
根据题意,可得售出的帽子的费用加上退回商家的费用减去购进帽子的费用,即可求解.
【详解】
解: .
故答案为: .
【点睛】
本题主要考查了整式的加减的应用,明确题意,准确列出代数式是解题的关键.
10.或
【分析】
根据题意列式计算即可得.
【详解】
解:当时:(元);
当x
【点睛】
本题考查了代数式,解题的关键是找出题意中的关系列出代数式.
11.144
【分析】
由图形可得,阴影部分的面积等于整个图形面积减去空白部分的面积,即可求解.
【详解】
解:由图形可得,阴影部分的面积等于整个图形面积减去空白部分的面积,
∵,
∴
故答案为:144.
【点睛】
此题考查了不规则图形的面积计算,解题的关键是不规则图形的面积转化为规则图形的面积,运用转化的思想.
12.ab-bc-ac+c2
【分析】
先求出矩形的面积(ab),再求出阴影部分的面积(ac和bc),两块交叉的部分面积是c2,根据图形求出即可.
【详解】
解:∵矩形ABCD的面积是ab,
阴影部分的面积是:ac+bc-c2,
∴图中空白部分的面积是:ab-(ac+bc-c2)=ab-bc-ac+c2.
故答案为:ab-bc-ac+c2.
【点睛】
本题考查了矩形的性质,平行四边形的性质,整式的运算的应用,注意:两块阴影部分的交叉处的面积是c2,题目比较好,但是一道比较容易出错的题目.
13.(6a-6b)米
【分析】
直接利用整式的加减运算法则计算得出答案.
【详解】
解:∵长方形的一边长为(2a-b)米,另一边比它短(a+b)米,
∴另一边为:2a-b-a b=a-2b,
∴这个正方形的周长是:2(2a-b+a-2b)=6a-6b.
故答案为:(6a-6b)米.
【点睛】
此题主要考查了整式的加减运算,正确掌握相关运算法则是解题关键.
14.4
【分析】
根据题意,可以得到,,,,,,从而可以发现题目中的数列以4,6,8依次循环出现,从而可以得到第2020个数的值.
【详解】
解:∵任意三个数的和为18,
∴①,
②,
③,
①+③-②得
,
∴,
∵,,
∴,
∴,
,
即,,,,,,
…,
∴,,,,,…的值三个一组循环,
∵,
∴.
故答案为:4.
【点睛】
本题考查数字的变化类,解答本题的关键是明确题意,发现数字的变化特点,写出第2020个数a2020的值.
15.
【分析】
根据题意列出算式,然后根据整式的运算法则即可求出答案.
【详解】
解:由题意可知宽为:.
故答案为:.
【点睛】
本题考查了整式的运算,熟练运用整式的运算法则是解题的关键.
16..
【分析】
根据题意可得A﹣B=,将代入其中求出A的代数式,然后再根据A+B计算即可.
【详解】
解:,,
,
即,
,
故答案为:.
【点睛】
本题主要考查了整式加减运算的实际运用,熟练掌握运算法则是解题关键.
17.(1);(2)木地板(-14x+86)平方米,地砖(14x+74)平方米;(3)总费用为(700x+27700)元.
【分析】
(1)根据长方形的对边相等可得2a=3+7,即可求出a的值;
(2)根据三间卧室铺设木地板,其它区域铺设地砖,可知将三间卧室的面积的和为木地板的面积,用长方形的面积-三间卧室的面积,所得的差为地砖的面积;
(3)根据所铺设面积和每种材料的单价,求出所需的费用即可.
【详解】
解:(1)根据题意得,
解得;
(2)铺设地面需要木地板:平方米;
铺设地面需要地砖:平方米;
(3)总费用=地砖费用+木地板费用
=,
则铺设地面的总费用为(700x+27700)元.
【点睛】
本题考查了列代数式,一元一次方程的应用.长方形的面积,分别求出铺设地面需要木地板与地砖的面积是解题的关键.
18.(1);(2);(3)
【分析】
(1)根据售价定为成本的2倍再降5元,并用当天销售额的1%作为整个直播团队的费用,列式即可;
(2)直接根据方案二的方式列式即可;
(3)根据总盈利=总销售额-总成本-直播团队的费用.
【详解】
解:(1)由题意可得:
直播团队的费用为:(元),
故答案为:;
(2)根据题意得:
方案二总销售额:
=,
故方案二总销售额为;
(3)方案一、方案二的总销售额=,
直播团队的费用为:元;
商品总成本为:,
总盈利=.
【点睛】
本题考查了列代数式,读懂题意,明确题中数量关系是解本题的关键.
19.(1);(2)
【分析】
(1)把图形分成半圆,一个大长方形和一个小长方形,由割补法即可求出面积;
(2)把,代入(1)中的式子即可得出答案.
【详解】
(1)由题可得:;
(2)当, 时,.
【点睛】
本题考查列代数式以及整式的运算,根据题意掌握用割补法表示面积是解题的关键.
20.(1);(2)平方米;(3)
【分析】
(1)根据纵向道路的宽是横向道路的宽的2倍即可求解;
(2)根据题意,由菜地的面积长方形的面积-道路的面积求解即可;
(3)根据菜地的面积长方形的面积-道路的面积分别求出、,再作差比较即可.
【详解】
解:(1)横向道路的宽是米,且纵向道路的宽是横向道路的宽的2倍,
纵向道路的宽是米,
故答案为:;
(2)由题意得:图1中菜地的面积为
平方米,
答:图1中菜地(阴影部分)的面积为平方米;
(3)由题意:图1中菜地的面积,
图2中横向道路的宽为米,纵向道路的宽为米,
∴图2中菜地的面积
平方米,
,
,
∴,
.
【点睛】
本题考查了列代数式、整式加减的应用、长方形的面积,正确表示出菜地的面积是解答的关键.
试卷第4页,共4页
试卷第3页,共4页
