2021-2022学年华东师大版数学八年级上册13.4.2作一个角等于已知角课件(共28张PPT)
文档属性
| 名称 | 2021-2022学年华东师大版数学八年级上册13.4.2作一个角等于已知角课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
13.4尺规作图
华东师大版八年级数学上册
数学王子 — 高斯
给我最大快乐的 :
不是已懂的知识,而是不断的学习;
不是已经达到的高度,而是继续不断地攀登 。
高斯
学习目标
1.了解尺规作图的定义;
2.掌握基本作图1和基本作图2;
3.会利用基本作图作三角形。
自学内容:P85前三段内容。
自学时间:(3分钟)
自学要求:思考以下内容,并填空。
1.什么是尺规作图。
2. 理解尺规作图的要求
3.研究的基本作图有哪几种?
自主学习
1.在几何里,把限定______________来作图,称为尺规作图。
2.常见的基本作图有:
(1)作______________;
(2)作______________;
(3)作_______________;
(4)经过一点作已知__________;
(5)作_______________。
自主学习
没有刻度的直尺和圆规
常见的基本作图有:
(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作已知角的平分线;
(4)经过一点作已知直线的垂线;
(5)作已知线段的垂直平分线。
知识梳理
1.在尺规作图中,直尺没有刻度不能进行度量,其作用是①画__ __ ;②连接___ _ ;圆规的作用是:①画 __ __ ;②度量比较 ____大小.
2.用尺规作图时,必须___ _____,
并注意作图的__ ____。
3、一定要写出结论哦。
直线、射线或线段
线段
圆或圆弧
线段
保留作图的痕迹
规范性
温馨提示
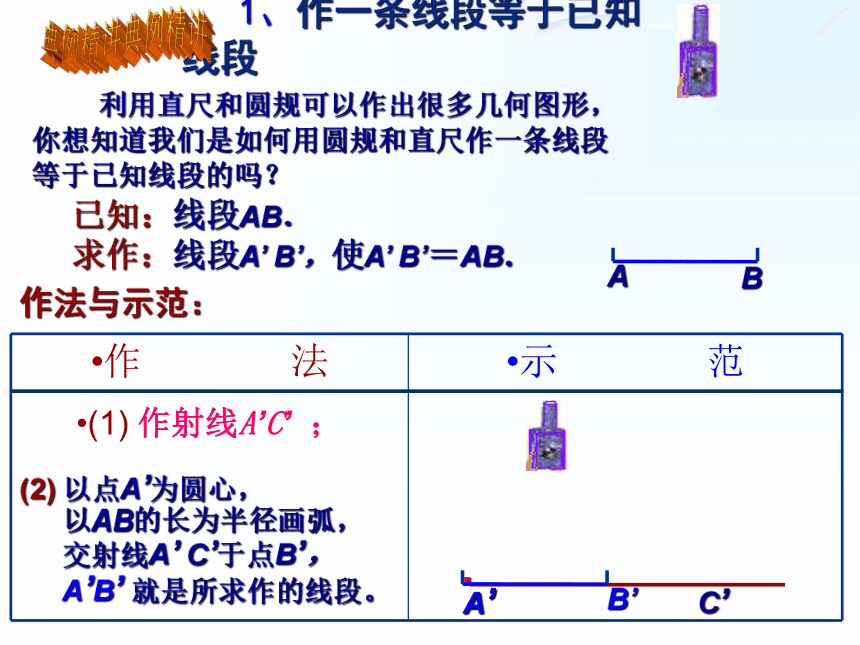
1、作一条线段等于已知线段
利用直尺和圆规可以作出很多几何图形,你想知道我们是如何用圆规和直尺作一条线段等于已知线段的吗?
已知:线段AB.
求作:线段A’ B’,使A’ B’=AB.
A
B
作法与示范:
(1) 作射线A’C’ ;
A’ C’
(2) 以点A’为圆心,
以AB的长为半径
画弧,
交射线A’ C’于点B’,
B’
A’
A’B’ 就是所求作的线段。
示 范
作 法
典例精讲
已知: ∠AOB。
B
O
A
求作: ∠A’O’B’ 使∠A’O’B’=∠AOB。
O’
A’
(2) 以点O为圆心,
任意长为半径
交OA于点C,
(3) 以点O’为圆心,
画弧,
C
D
同样(OC)长为半径
画弧,
C’
(4) 以点C’为圆心,
CD长为半径
画弧,
D’
(5) 过点D’作射线O’B’.
B’
A’
O’
B’
∠A’O’B’就是所求的角.
作 法 示 范
(1) 作射线O’A’;
交OB于点D;
交O’A’于点C’;
交前面的弧于点D’ ,
(2)作一个角等于已知角
典例精讲
想一想:为什么两个角相等?你会证明吗?
想一想:
奖励:
1.回答问题 个人 奖励
所在小组 奖励
2.纠错补充的同学奖励
就位与展示
大家都听得非常认真,
上面都掌握了么?
让我们来试试下一道题吧!!
活动形式:抢答
要求:
1.讲题的同学声音洪亮,
2.作图语言要规范。
小组清零
活动形式:抢答
1、任意画出两条线段AB和CD,再作一条线段,使它等于AB+2CD
独立思考、合作交流;
口述作法、保留作图痕迹。
就位与展示
2、已知: ∠AOB。
利用尺规作: ∠A’O’B’(不在原图上作)
使∠A’O’B’=2∠AOB。
B
O
A
做法
C’
E
B’
O’
A
∠A’O’B’为所求.
就位与展示
C
D
题目:能力提升 第1,2,题
要求:
1. 每个小组随机抽一道题目。
2. 组长合理分工,小白板展示
(画图 讲解思路 )
3.讲题的同学声音洪亮!!
4.其他小组同学认真聆听 纠错补充
抢星夺旗
小组清零
1
2
抢星夺旗
1
2
1
2
2星3旗
2星2旗
2星3旗
2星2旗
2星1旗
2星2旗
重庆中考
1.画△ABC,使其两边为已知线段a、b,夹角为β.(要求:用尺规作图,写出已知、求作;保留作图痕迹;不在已知的线、角上作图;不写作法).
已知:线段a、b、角β 求作:△ABC使边BC=a,AC=b,∠C=β
能力提升
作法:
(1)作∠A=∠α ;
(2)在AB上截取AB=m ,AC=n;
(3)连接BC。
则△ABC就是所求作的三角形
2.已知:线段a、b 、c.
求作:△ABC,使AB= c ,BC= a ,
AC= b.
c
b
a
能力提升
解:已知:线段a、b、角β(1分) 求作:△ABC使边BC=a,AC=b,∠C=β(2分) 画图(保留作图痕迹)(6分)
分析:根据一个三角形的两边分别为a,b,这两边的夹角为α,做一条射线CA,在原角上以任意长度为半径画弧,再以C为圆心,相同长度为半径画弧作出∠BCA=∠β,即可得出△ABC.
点评:此题主要考查了作一个角等于已知角,根据已知线段画出三角形,作出已知角是解决问题的关键.
3:已知两角及夹边作三角形。
已知:如图,∠α ,∠β ,线段m .
求作:△ABC,使∠A=∠α ,∠B=∠β ,AB=m.
作法:
作线段AB=m;
在AB的同旁
作∠A=∠α ,作∠B=∠β ,
∠A与∠B的另一边相交于C。
则△ABC就是所求作的图形(三角形)。
变式思维
已知△ABC,用直尺和圆规作△DEF,使△DEF≌△ABC,
并说出你选择的作图方法
。
拓展创新
1.下列作图规范的是( )
A.延长线段AB; B.以点O为圆心作弧
C.以OA为半径作弧;D.在射线OF上截OA=5cm.
达标检测
2.用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( )(2014安顺)
A. (SAS) B. (SSS)
C. (ASA) D. (AAS)
3.利用尺规作图不能唯一作出三角形的是( )
A.已知三边 B.已知两边及夹角
C.已知两角及夹边
D.已知两边及其中一边的对角
4.已知:∠1和∠2
求作:∠AOB,使∠AOB=∠1+∠2
1
2
通过本节课的学习你有哪些收获?
课堂小结
你还有什么想法吗?
用尺规作优美的图案
试一试
右面的“邹菊图案”漂亮吗?
你想自己画出它来吗?
那就让我们从最初的步骤开始吧!
4、继续作下去,
以点O为圆心,
r 为半径作圆O;
1、
以圆O上任意一点为圆心,
r 为半径作圆,与圆O交于两点;
2、
分别以两个交点为圆心,
r 为半径作圆;
3、
在适当的区域涂上颜色,
你作出美丽的“邹菊图案” 吗?
学困生:P91习题13.4第1,2题
中优等生:附加:拓展延伸:1.
作业布置
已知直线AB及直线AB外一点C,过点C作CD∥AB(写出作法,画出图形).
拓展延伸
你知道被称为几何三大问题的古典难题么?你能用尺规作图三等分角么?
给我最大快乐的 :
不是已懂的知识,而是不断的学习;
不是已经达到的高度,而是继续不断地攀登
不断的学习
不断地攀登
13.4尺规作图
华东师大版八年级数学上册
数学王子 — 高斯
给我最大快乐的 :
不是已懂的知识,而是不断的学习;
不是已经达到的高度,而是继续不断地攀登 。
高斯
学习目标
1.了解尺规作图的定义;
2.掌握基本作图1和基本作图2;
3.会利用基本作图作三角形。
自学内容:P85前三段内容。
自学时间:(3分钟)
自学要求:思考以下内容,并填空。
1.什么是尺规作图。
2. 理解尺规作图的要求
3.研究的基本作图有哪几种?
自主学习
1.在几何里,把限定______________来作图,称为尺规作图。
2.常见的基本作图有:
(1)作______________;
(2)作______________;
(3)作_______________;
(4)经过一点作已知__________;
(5)作_______________。
自主学习
没有刻度的直尺和圆规
常见的基本作图有:
(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作已知角的平分线;
(4)经过一点作已知直线的垂线;
(5)作已知线段的垂直平分线。
知识梳理
1.在尺规作图中,直尺没有刻度不能进行度量,其作用是①画__ __ ;②连接___ _ ;圆规的作用是:①画 __ __ ;②度量比较 ____大小.
2.用尺规作图时,必须___ _____,
并注意作图的__ ____。
3、一定要写出结论哦。
直线、射线或线段
线段
圆或圆弧
线段
保留作图的痕迹
规范性
温馨提示
1、作一条线段等于已知线段
利用直尺和圆规可以作出很多几何图形,你想知道我们是如何用圆规和直尺作一条线段等于已知线段的吗?
已知:线段AB.
求作:线段A’ B’,使A’ B’=AB.
A
B
作法与示范:
(1) 作射线A’C’ ;
A’ C’
(2) 以点A’为圆心,
以AB的长为半径
画弧,
交射线A’ C’于点B’,
B’
A’
A’B’ 就是所求作的线段。
示 范
作 法
典例精讲
已知: ∠AOB。
B
O
A
求作: ∠A’O’B’ 使∠A’O’B’=∠AOB。
O’
A’
(2) 以点O为圆心,
任意长为半径
交OA于点C,
(3) 以点O’为圆心,
画弧,
C
D
同样(OC)长为半径
画弧,
C’
(4) 以点C’为圆心,
CD长为半径
画弧,
D’
(5) 过点D’作射线O’B’.
B’
A’
O’
B’
∠A’O’B’就是所求的角.
作 法 示 范
(1) 作射线O’A’;
交OB于点D;
交O’A’于点C’;
交前面的弧于点D’ ,
(2)作一个角等于已知角
典例精讲
想一想:为什么两个角相等?你会证明吗?
想一想:
奖励:
1.回答问题 个人 奖励
所在小组 奖励
2.纠错补充的同学奖励
就位与展示
大家都听得非常认真,
上面都掌握了么?
让我们来试试下一道题吧!!
活动形式:抢答
要求:
1.讲题的同学声音洪亮,
2.作图语言要规范。
小组清零
活动形式:抢答
1、任意画出两条线段AB和CD,再作一条线段,使它等于AB+2CD
独立思考、合作交流;
口述作法、保留作图痕迹。
就位与展示
2、已知: ∠AOB。
利用尺规作: ∠A’O’B’(不在原图上作)
使∠A’O’B’=2∠AOB。
B
O
A
做法
C’
E
B’
O’
A
∠A’O’B’为所求.
就位与展示
C
D
题目:能力提升 第1,2,题
要求:
1. 每个小组随机抽一道题目。
2. 组长合理分工,小白板展示
(画图 讲解思路 )
3.讲题的同学声音洪亮!!
4.其他小组同学认真聆听 纠错补充
抢星夺旗
小组清零
1
2
抢星夺旗
1
2
1
2
2星3旗
2星2旗
2星3旗
2星2旗
2星1旗
2星2旗
重庆中考
1.画△ABC,使其两边为已知线段a、b,夹角为β.(要求:用尺规作图,写出已知、求作;保留作图痕迹;不在已知的线、角上作图;不写作法).
已知:线段a、b、角β 求作:△ABC使边BC=a,AC=b,∠C=β
能力提升
作法:
(1)作∠A=∠α ;
(2)在AB上截取AB=m ,AC=n;
(3)连接BC。
则△ABC就是所求作的三角形
2.已知:线段a、b 、c.
求作:△ABC,使AB= c ,BC= a ,
AC= b.
c
b
a
能力提升
解:已知:线段a、b、角β(1分) 求作:△ABC使边BC=a,AC=b,∠C=β(2分) 画图(保留作图痕迹)(6分)
分析:根据一个三角形的两边分别为a,b,这两边的夹角为α,做一条射线CA,在原角上以任意长度为半径画弧,再以C为圆心,相同长度为半径画弧作出∠BCA=∠β,即可得出△ABC.
点评:此题主要考查了作一个角等于已知角,根据已知线段画出三角形,作出已知角是解决问题的关键.
3:已知两角及夹边作三角形。
已知:如图,∠α ,∠β ,线段m .
求作:△ABC,使∠A=∠α ,∠B=∠β ,AB=m.
作法:
作线段AB=m;
在AB的同旁
作∠A=∠α ,作∠B=∠β ,
∠A与∠B的另一边相交于C。
则△ABC就是所求作的图形(三角形)。
变式思维
已知△ABC,用直尺和圆规作△DEF,使△DEF≌△ABC,
并说出你选择的作图方法
。
拓展创新
1.下列作图规范的是( )
A.延长线段AB; B.以点O为圆心作弧
C.以OA为半径作弧;D.在射线OF上截OA=5cm.
达标检测
2.用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( )(2014安顺)
A. (SAS) B. (SSS)
C. (ASA) D. (AAS)
3.利用尺规作图不能唯一作出三角形的是( )
A.已知三边 B.已知两边及夹角
C.已知两角及夹边
D.已知两边及其中一边的对角
4.已知:∠1和∠2
求作:∠AOB,使∠AOB=∠1+∠2
1
2
通过本节课的学习你有哪些收获?
课堂小结
你还有什么想法吗?
用尺规作优美的图案
试一试
右面的“邹菊图案”漂亮吗?
你想自己画出它来吗?
那就让我们从最初的步骤开始吧!
4、继续作下去,
以点O为圆心,
r 为半径作圆O;
1、
以圆O上任意一点为圆心,
r 为半径作圆,与圆O交于两点;
2、
分别以两个交点为圆心,
r 为半径作圆;
3、
在适当的区域涂上颜色,
你作出美丽的“邹菊图案” 吗?
学困生:P91习题13.4第1,2题
中优等生:附加:拓展延伸:1.
作业布置
已知直线AB及直线AB外一点C,过点C作CD∥AB(写出作法,画出图形).
拓展延伸
你知道被称为几何三大问题的古典难题么?你能用尺规作图三等分角么?
给我最大快乐的 :
不是已懂的知识,而是不断的学习;
不是已经达到的高度,而是继续不断地攀登
不断的学习
不断地攀登
